2021-2022学年人教版九年级数学上册第22章 二次函数复习与总结课件(15张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第22章 二次函数复习与总结课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
空白演示
第22章
二次函数复习与总结
知识点一
二次函数的定义
一般地,如果y=ax2+bx+c
(a,b,c是常数,a≠0),那么y叫做x的二次函数.
注意:二次项系数a≠0;自变量x的最高次数是2.
思考:常数b和c可以为0吗?
其中二次项为ax2,一次项为bx,常数项c
二次项的系数为a,一次项的系数为b,常数项c
知识点二:二次函数的表达式:
二次函数的一般式:y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
2.二次函数顶点式:
y=a(x-h)2+k(a≠0)。
3.二次函数的交点式:y=a(x-x1)(x-x2)(a≠0)。
问题2:描点法画函数图象的一般步骤是哪些?
1.列---列表(表中给出一些自变量的值及其对应的函数值);
2.描---描点(在直角坐标系中描出表中数值对应的各点);
3.连---连线(按照横坐标由小到大的顺序把所描各点用平滑的曲线连接起来).
问题1:一般用什么方法画函数的图象?
知识点三
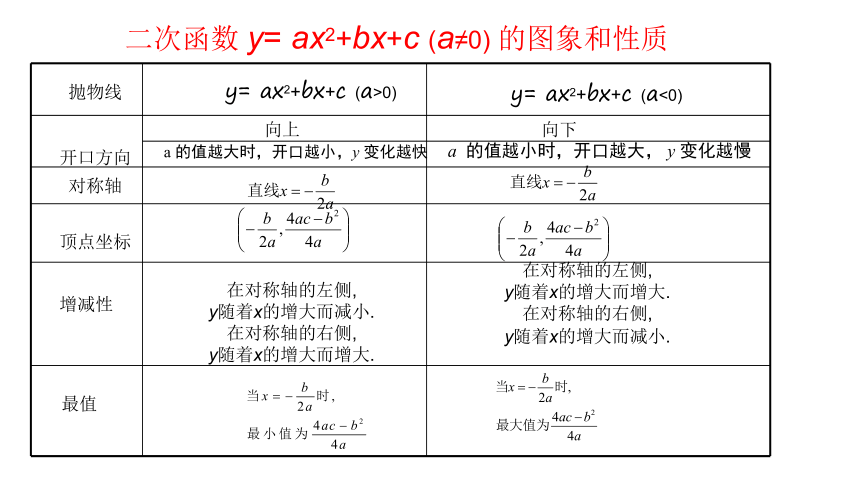
二次函数的图象和性质
二次函数
y=
ax2+bx+c
(a≠0)
的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=
ax2+bx+c
(a>0)
向上
向下
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
y=
ax2+bx+c
(a<0)
a
的值越大时,开口越小,y
变化越快
a
的值越小时,开口越大,
y
变化越慢
如何根据图像判别a、b、c、b2-4ac,2a+b,a+b+c的符号
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
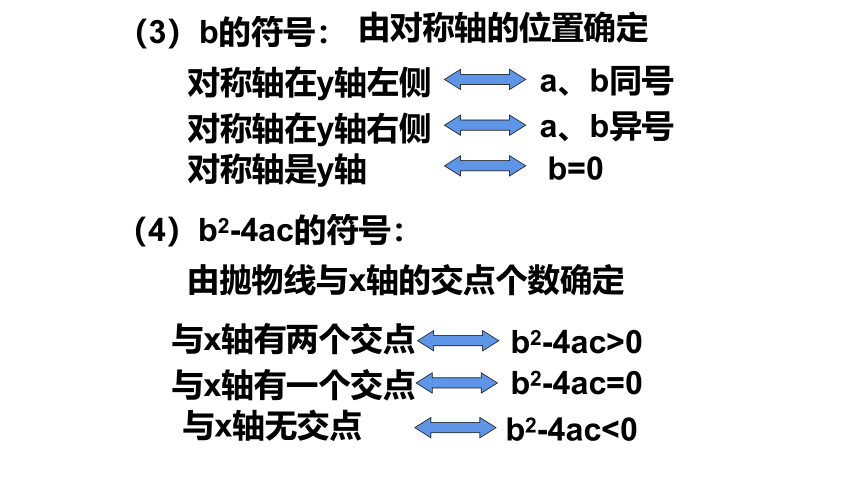
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的.
y
=
ax2
y
=
ax2
+
k
y
=
a(x
-
h
)2
y
=
a(
x
-
h
)2
+
k
上下平移
左右平移
上下平移
左右平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
知识点四:
注意:当二次函数为y=
ax2+bx+c,需先将二次函数化为顶点式再按平移的规律进行平移。
抛物线已知条件
二次函数解析式形式(a≠0)
三个点的坐标
顶点及另一点坐标
与x轴两交点横坐标及另一点坐标
知识点五:求抛物线解析式常用的三种方法
一般式
y=ax2+bx+c
顶点式
y=a(x-h)2+k
交点式
y=a(x-x1)(x-x2)
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
O
O
x1=
x2
x
y
x
O
y
△>0
△=0
△<0
x1
;
x2
x1
=x2=-b/2a
没有实数根
xx2
x
≠
x1的一切实数
所有实数
x1无解
无解
知识点六:二次函数与一元二次方程,一元二次不等式的关系
y=
ax2+bx+c
利用二次函数解决实际问题
图形的面积问题
销售利润问题
抛物线性问题
利用图形的面积公式建立相应的函数关系式
根据相关线段的长度大于0确定自变量的取值范围
配方变形,或利用公式在自变量的取值范围内求它的最大值或最小值
建立函数关系式:总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
在自变量的取值范围内确定最大利润
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
②选择运算简便的方法.
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
2、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为(
)
B
1、函数
是二次函数,则a=_______
课堂练习
3
3、抛物线
向右平移1个单位,再向下平移2个单位,得到抛物线
,则a+b+c=_____
4、
已知函数的图象如图所示,求函数解析式。
-1
3
3
x
y
0
解:
设函数的解析式为:y=a(x-x1)(x-x2),
则
x1=-1,
x2=3,
于是
y=a(x+1)(x-3).
∵抛物线过y
轴上的点(0,3),
∴把这点坐标代入上面式子,得
3=-3a
∴
a=-1.
∴
所求函数解析式为:
y=-1(x+1)(x-3).
即
y=
-
x2+2x+3
.
-1
5、二次函数
y=ax2+bx+c
的图象如图所示,试用
“
>、<
、=”
填空:
(1)a
0,b
0,
c
0;
(2)a+b+c
0;
(3)a-b+c
0;
(4)
△
0;
(5)
0.
-1
x
y
0
1
1
<
<
>
<
>
>
>
6.某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养
费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1,
∴y=x2+x.
(2)设g=33x-100-x2-x,则
g=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时,g随x的增大而增大,故当x=4时,即第4年可收回投资。
空白演示
第22章
二次函数复习与总结
知识点一
二次函数的定义
一般地,如果y=ax2+bx+c
(a,b,c是常数,a≠0),那么y叫做x的二次函数.
注意:二次项系数a≠0;自变量x的最高次数是2.
思考:常数b和c可以为0吗?
其中二次项为ax2,一次项为bx,常数项c
二次项的系数为a,一次项的系数为b,常数项c
知识点二:二次函数的表达式:
二次函数的一般式:y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
2.二次函数顶点式:
y=a(x-h)2+k(a≠0)。
3.二次函数的交点式:y=a(x-x1)(x-x2)(a≠0)。
问题2:描点法画函数图象的一般步骤是哪些?
1.列---列表(表中给出一些自变量的值及其对应的函数值);
2.描---描点(在直角坐标系中描出表中数值对应的各点);
3.连---连线(按照横坐标由小到大的顺序把所描各点用平滑的曲线连接起来).
问题1:一般用什么方法画函数的图象?
知识点三
二次函数的图象和性质
二次函数
y=
ax2+bx+c
(a≠0)
的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=
ax2+bx+c
(a>0)
向上
向下
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
y=
ax2+bx+c
(a<0)
a
的值越大时,开口越小,y
变化越快
a
的值越小时,开口越大,
y
变化越慢
如何根据图像判别a、b、c、b2-4ac,2a+b,a+b+c的符号
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的.
y
=
ax2
y
=
ax2
+
k
y
=
a(x
-
h
)2
y
=
a(
x
-
h
)2
+
k
上下平移
左右平移
上下平移
左右平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
知识点四:
注意:当二次函数为y=
ax2+bx+c,需先将二次函数化为顶点式再按平移的规律进行平移。
抛物线已知条件
二次函数解析式形式(a≠0)
三个点的坐标
顶点及另一点坐标
与x轴两交点横坐标及另一点坐标
知识点五:求抛物线解析式常用的三种方法
一般式
y=ax2+bx+c
顶点式
y=a(x-h)2+k
交点式
y=a(x-x1)(x-x2)
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
O
O
x1=
x2
x
y
x
O
y
△>0
△=0
△<0
x1
;
x2
x1
=x2=-b/2a
没有实数根
x
x
≠
x1的一切实数
所有实数
x1
无解
知识点六:二次函数与一元二次方程,一元二次不等式的关系
y=
ax2+bx+c
利用二次函数解决实际问题
图形的面积问题
销售利润问题
抛物线性问题
利用图形的面积公式建立相应的函数关系式
根据相关线段的长度大于0确定自变量的取值范围
配方变形,或利用公式在自变量的取值范围内求它的最大值或最小值
建立函数关系式:总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
在自变量的取值范围内确定最大利润
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
②选择运算简便的方法.
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
2、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为(
)
B
1、函数
是二次函数,则a=_______
课堂练习
3
3、抛物线
向右平移1个单位,再向下平移2个单位,得到抛物线
,则a+b+c=_____
4、
已知函数的图象如图所示,求函数解析式。
-1
3
3
x
y
0
解:
设函数的解析式为:y=a(x-x1)(x-x2),
则
x1=-1,
x2=3,
于是
y=a(x+1)(x-3).
∵抛物线过y
轴上的点(0,3),
∴把这点坐标代入上面式子,得
3=-3a
∴
a=-1.
∴
所求函数解析式为:
y=-1(x+1)(x-3).
即
y=
-
x2+2x+3
.
-1
5、二次函数
y=ax2+bx+c
的图象如图所示,试用
“
>、<
、=”
填空:
(1)a
0,b
0,
c
0;
(2)a+b+c
0;
(3)a-b+c
0;
(4)
△
0;
(5)
0.
-1
x
y
0
1
1
<
<
>
<
>
>
>
6.某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养
费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1,
∴y=x2+x.
(2)设g=33x-100-x2-x,则
g=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时,g随x的增大而增大,故当x=4时,即第4年可收回投资。
同课章节目录
