人教版 六年级数学上册5.2圆的面积课件(20张PPT)
文档属性
| 名称 | 人教版 六年级数学上册5.2圆的面积课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 20:29:17 | ||
图片预览


文档简介
(共19张PPT)
3.圆的面积
六年级数学上册(RJ) 教学课件
第2课时 圆环的面积
5 圆
5 圆
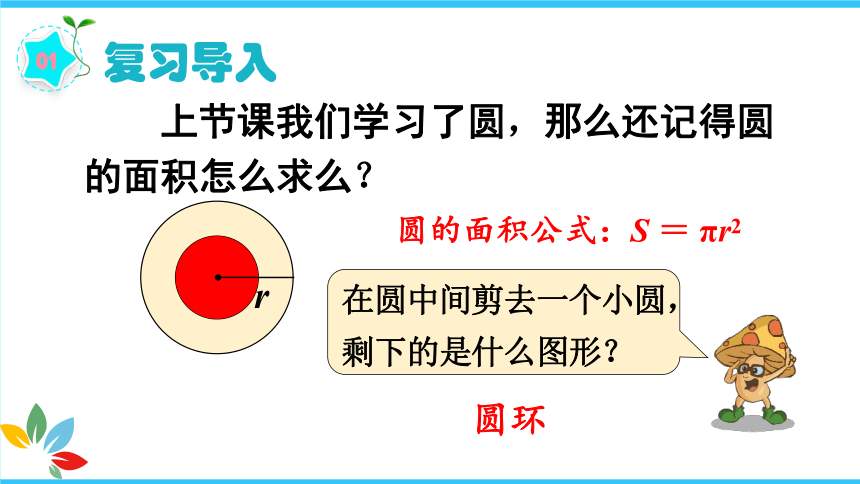
上节课我们学习了圆,那么还记得圆的面积怎么求么?
圆的面积公式:S = πr2
在圆中间剪去一个小圆,剩下的是什么图形?
r
圆环
01
复习导入
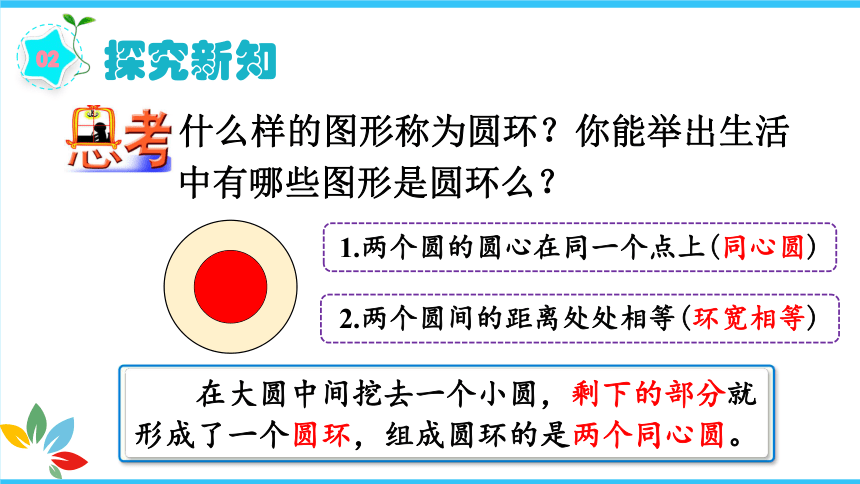
什么样的图形称为圆环?你能举出生活中有哪些图形是圆环么?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
1.两个圆的圆心在同一个点上(同心圆)
2.两个圆间的距离处处相等(环宽相等)
02
探究新知
生活中的圆环
游泳圈
光盘
摩天轮
汽车
轮胎
······
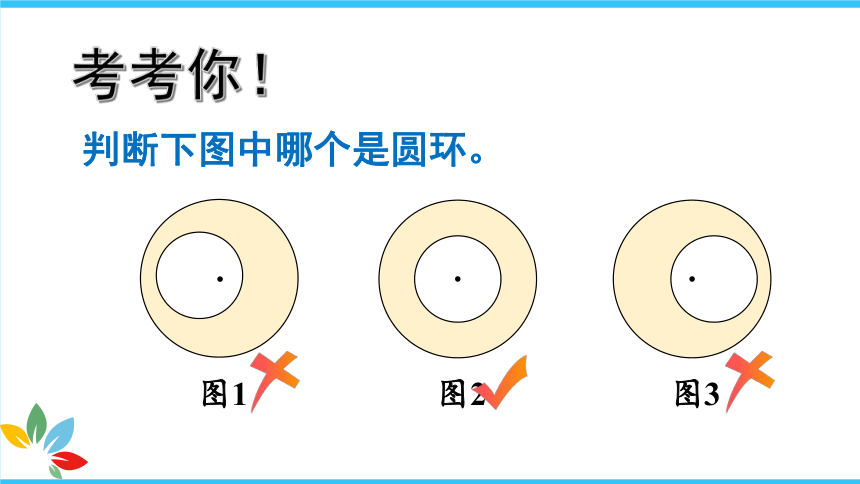
判断下图中哪个是圆环。
考考你!
图1
图2
图3
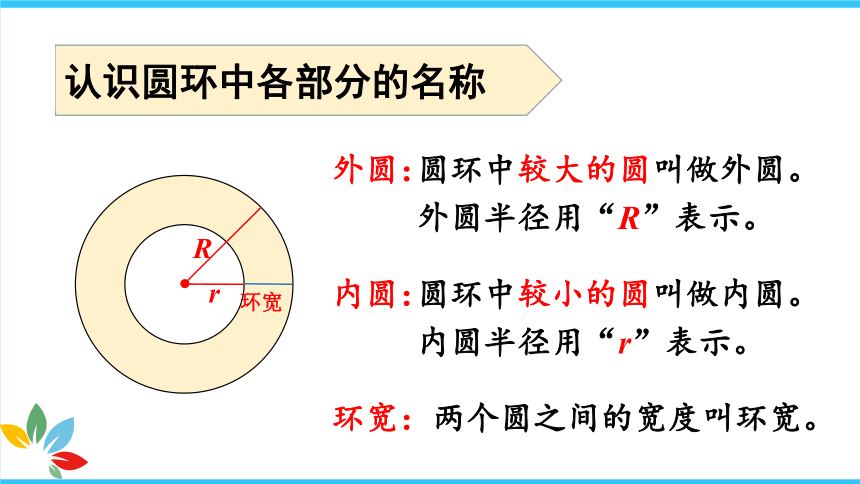
认识圆环中各部分的名称
外圆:
圆环中较大的圆叫做外圆。
外圆半径用“R”表示。
r
R
内圆:
圆环中较小的圆叫做内圆。
内圆半径用“r”表示。
环宽:两个圆之间的宽度叫环宽。
环宽
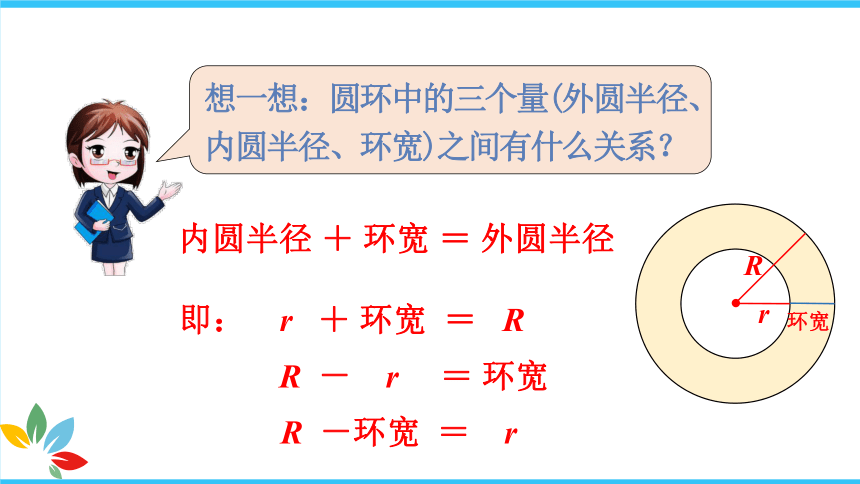
想一想:圆环中的三个量(外圆半径、内圆半径、环宽)之间有什么关系?
内圆半径 + 环宽 = 外圆半径
即: r + 环宽 = R
R - r = 环宽
R -环宽 = r
r
R
环宽
圆环的面积应该怎么计算呢?
R
r
观察图形,不难发现:
圆环的面积=外圆面积-内圆面积。
即 S圆环=πR2-πr2=π(R2-r2)。
-
=
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
已知内圆和外圆的半径,我可以先分别求出外圆和内圆的面积,然后相减就可以得出圆环的面积。
3.14×62 - 3.14×22
=3.14×36 -3.14×4
=100.48(cm2)
答:圆环的面积是100.48 cm2。
已知内圆和外圆的半径,我可以根据圆环的面积公式:
S圆环=πR2-πr2=π(R2-r2)直接计算。
3.14×(62 - 22)
=3.14×32
=100.48(cm2)
答:圆环的面积是100.48 cm2。
若已知圆环的外圆直径(D)和内圆直径(d),圆环的面积应该怎么求呢?
若已知圆环的外圆周长(C外)和内圆周长(C内),圆环的面积应该怎么求呢?
1.一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
(教材P68“做一做”第2题)
03
学以致用
环形草坪的外圆半径为:50÷2=25(m)
答:草坪的占地面积是1884m2。
环形草坪的面积为:
内圆半径为:10÷2=5(m)
S =π(R2-r2)
=3.14×(252- 52)
=3.14×600
=1884(m2)
2.右图是一块玉璧,外直径18 cm,内直径7 cm,这块玉璧的面积是多少?
(教材P72“练习十五”第5题)
这块玉璧的外圆半径为:18÷2=9(cm)
答:这块玉璧的面积是215.875cm2。
面积为:S =π(R2-r2)
内圆半径为:7÷2=3.5(cm)
=3.14×(92 -3.52)
=3.14×68.75
=215.875(cm2)
3.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
(教材P72“练习十五”第6题)
由图知,大圆半径为:6cm,
答:阴影部分的面积是84.78cm2。
则阴影部分面积为:S =π(R2-r2)
小圆半径为:6÷2=3(cm)
=3.14×(62 -32)
=3.14×27
=84.78(cm2)
04
课堂小结
圆环的面积
1.由半径不相等的两个同心圆围成的环状图形,叫做圆环。
2.圆环的面积公式:
圆环的面积 = 外圆面积 - 内圆面积
即 S圆环=πR2-πr2=π(R2-r2)。
3.圆的面积
六年级数学上册(RJ) 教学课件
第2课时 圆环的面积
5 圆
5 圆
上节课我们学习了圆,那么还记得圆的面积怎么求么?
圆的面积公式:S = πr2
在圆中间剪去一个小圆,剩下的是什么图形?
r
圆环
01
复习导入
什么样的图形称为圆环?你能举出生活中有哪些图形是圆环么?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
1.两个圆的圆心在同一个点上(同心圆)
2.两个圆间的距离处处相等(环宽相等)
02
探究新知
生活中的圆环
游泳圈
光盘
摩天轮
汽车
轮胎
······
判断下图中哪个是圆环。
考考你!
图1
图2
图3
认识圆环中各部分的名称
外圆:
圆环中较大的圆叫做外圆。
外圆半径用“R”表示。
r
R
内圆:
圆环中较小的圆叫做内圆。
内圆半径用“r”表示。
环宽:两个圆之间的宽度叫环宽。
环宽
想一想:圆环中的三个量(外圆半径、内圆半径、环宽)之间有什么关系?
内圆半径 + 环宽 = 外圆半径
即: r + 环宽 = R
R - r = 环宽
R -环宽 = r
r
R
环宽
圆环的面积应该怎么计算呢?
R
r
观察图形,不难发现:
圆环的面积=外圆面积-内圆面积。
即 S圆环=πR2-πr2=π(R2-r2)。
-
=
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
已知内圆和外圆的半径,我可以先分别求出外圆和内圆的面积,然后相减就可以得出圆环的面积。
3.14×62 - 3.14×22
=3.14×36 -3.14×4
=100.48(cm2)
答:圆环的面积是100.48 cm2。
已知内圆和外圆的半径,我可以根据圆环的面积公式:
S圆环=πR2-πr2=π(R2-r2)直接计算。
3.14×(62 - 22)
=3.14×32
=100.48(cm2)
答:圆环的面积是100.48 cm2。
若已知圆环的外圆直径(D)和内圆直径(d),圆环的面积应该怎么求呢?
若已知圆环的外圆周长(C外)和内圆周长(C内),圆环的面积应该怎么求呢?
1.一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
(教材P68“做一做”第2题)
03
学以致用
环形草坪的外圆半径为:50÷2=25(m)
答:草坪的占地面积是1884m2。
环形草坪的面积为:
内圆半径为:10÷2=5(m)
S =π(R2-r2)
=3.14×(252- 52)
=3.14×600
=1884(m2)
2.右图是一块玉璧,外直径18 cm,内直径7 cm,这块玉璧的面积是多少?
(教材P72“练习十五”第5题)
这块玉璧的外圆半径为:18÷2=9(cm)
答:这块玉璧的面积是215.875cm2。
面积为:S =π(R2-r2)
内圆半径为:7÷2=3.5(cm)
=3.14×(92 -3.52)
=3.14×68.75
=215.875(cm2)
3.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
(教材P72“练习十五”第6题)
由图知,大圆半径为:6cm,
答:阴影部分的面积是84.78cm2。
则阴影部分面积为:S =π(R2-r2)
小圆半径为:6÷2=3(cm)
=3.14×(62 -32)
=3.14×27
=84.78(cm2)
04
课堂小结
圆环的面积
1.由半径不相等的两个同心圆围成的环状图形,叫做圆环。
2.圆环的面积公式:
圆环的面积 = 外圆面积 - 内圆面积
即 S圆环=πR2-πr2=π(R2-r2)。
