人教版 六年级数学上册5.3圆的面积课件(22张PPT)
文档属性
| 名称 | 人教版 六年级数学上册5.3圆的面积课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 11:10:11 | ||
图片预览






文档简介
(共21张PPT)
3.圆的面积
六年级数学上册(RJ) 教学课件
第3课时 解决问题
5 圆
5 圆
万汇楼
古铜钱
外方内圆 外圆内方
中式屏风
中式屏风
01
情境导入
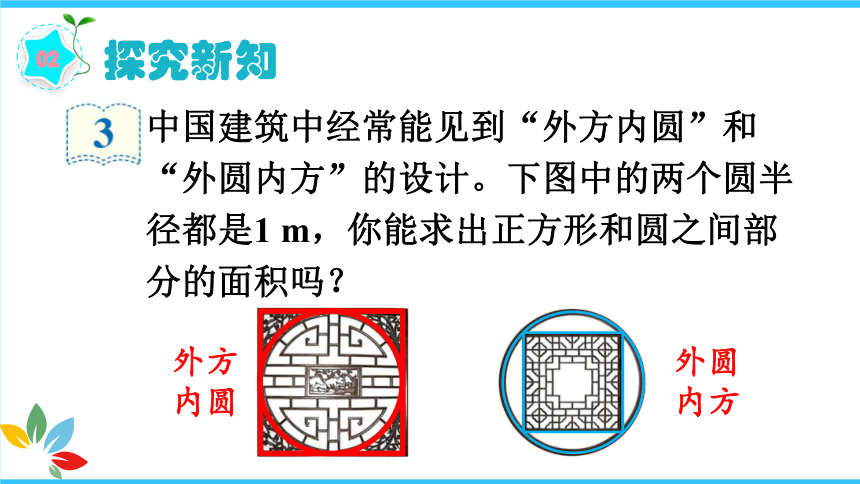
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?
外方内圆
外圆内方
02
探究新知
阅读与理解
两个圆的半径都是1m。
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积。
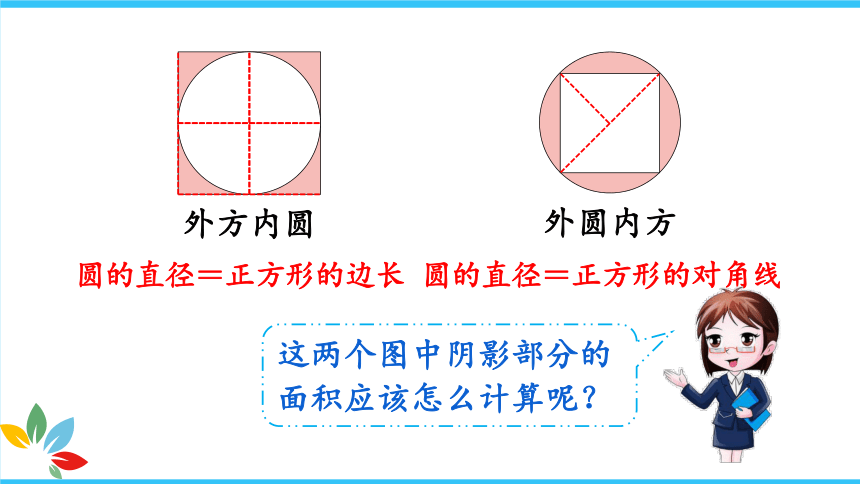
外方内圆
外圆内方
圆的直径=正方形的边长
圆的直径=正方形的对角线
这两个图中阴影部分的面积应该怎么计算呢?
分析与解答
从图中可以看出:正方形的边长与圆的直径长度相等,且阴影部分的面积=正方形的面积-圆的面积。
正方形的边长:1×2=2(m)
正方形的面积:2×2=4(m2)
圆的面积:3.14×12=3.14(m2)
阴影部分的面积:4-3.14=0.86(m2)
我们可以把右图中的正方形看成两个三角形,它的底边就是圆的直径,高就是圆的半径。且阴影部分的面积=圆的面积-正方形的面积。
一个三角形的面积为:
阴影部分的面积:3.14-2=1.14(m2)
正方形的面积为:2×1=2(m2)
回顾与反思
r
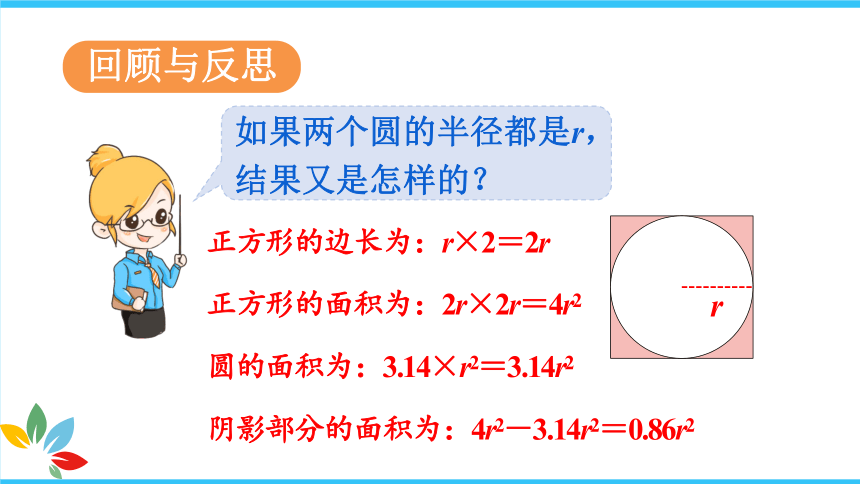
正方形的边长为:r×2=2r
正方形的面积为:2r×2r=4r2
圆的面积为:3.14×r2=3.14r2
阴影部分的面积为:4r2-3.14r2=0.86r2
如果两个圆的半径都是r,结果又是怎样的?
当r=1m时,和前面的计算结果完全一致。
一个三角形的面积为:
阴影部分的面积:3.14r2-2r2=1.14r2
正方形的面积为:2×r2=2r2
当圆的半径为r时,右图中:
答:左图中正方形与圆之间的面积是0.86 m2,
右图中圆与正方形之间的面积是1.14m2。
r
如果你仔细观察就会发现:我们周围很多东西的平面轮廓都是圆形的,如车轮、马路上的大多数井盖······这是为什么呢?
生活中的数学
车轮平面轮廓采用圆形,是利用同一圆的半径都相等的性质,把车轴装在车轮的圆心上。当车轮在地面上滚动的时候,车轴离地面的距离总是等于车轮的半径,因此只要道路平坦,车子就会平稳地在地面上行驶。试想一下,如果车轮是正方形的,为了保持车辆的平稳行驶,道路应该是什么样子的呢?
生活中的数学
井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,这里利用了同一圆的直径都相等的性质。
生活中的数学
1.下图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
(教材P70“做一做”)
03
学以致用
正方形的面积为:
24×(24÷2)÷2×2=288(cm2)
圆的面积为:3.14×(24÷2)2=452.16(cm2)
外面的圆与内部的正方形之间的面积为:
452.16-288=164.16(cm2)
答:外面的圆与内部的正方形之间的面积是164.16cm2。
2.下图中的铜钱直径28 mm,中间的正方形边长为6 mm。这个铜钱的面积是多少?
(教材P72“练习十五”第9题)
正方形的面积为:6×6=36(mm2)
圆的面积为:
3.14×(28÷2)2=615.44(mm2)
这个铜钱的面积为:615.44-36=579.44(mm2)
答:铜钱的面积为579.44mm2。
3.一个运动场如图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P73“练习十五”第10题)
C =2×C半圆+2×100 m
=2×3.14×32+2×100
=200.96+200
=400.96(米)
3.一个运动场如图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P73“练习十五”第10题)
S =2×S半圆+S长方形
=2×(3.14×322÷2)+(2×32)×100
=3215.36+6400
=9615.36(平方米)
答:这个运动场的周长是400.96米,面积是9615.36平方米。
4.一个圆的周长是62.8 m,半径增加了2 m后,面积增加了多少?
(教材P73“练习十五”第13题)
增加2 m后的半径变为:10+2=12(m)
圆的半径
半径增加后的面积为:3.14×122=452.16(m2)
答:面积增加了138.16m2。
增加之前的面积为:3.14×102=314(m2)
面积增加了:452.16-314 =138.16(m2)
04
课堂小结
“外圆内方,外方内圆”图形面积的计算
1.在“外方内圆”图形中,圆的直径等于正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2.在“外圆内方”图形中,这个正方形的对角线等于圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r 。
3.圆的面积
六年级数学上册(RJ) 教学课件
第3课时 解决问题
5 圆
5 圆
万汇楼
古铜钱
外方内圆 外圆内方
中式屏风
中式屏风
01
情境导入
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?
外方内圆
外圆内方
02
探究新知
阅读与理解
两个圆的半径都是1m。
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积。
外方内圆
外圆内方
圆的直径=正方形的边长
圆的直径=正方形的对角线
这两个图中阴影部分的面积应该怎么计算呢?
分析与解答
从图中可以看出:正方形的边长与圆的直径长度相等,且阴影部分的面积=正方形的面积-圆的面积。
正方形的边长:1×2=2(m)
正方形的面积:2×2=4(m2)
圆的面积:3.14×12=3.14(m2)
阴影部分的面积:4-3.14=0.86(m2)
我们可以把右图中的正方形看成两个三角形,它的底边就是圆的直径,高就是圆的半径。且阴影部分的面积=圆的面积-正方形的面积。
一个三角形的面积为:
阴影部分的面积:3.14-2=1.14(m2)
正方形的面积为:2×1=2(m2)
回顾与反思
r
正方形的边长为:r×2=2r
正方形的面积为:2r×2r=4r2
圆的面积为:3.14×r2=3.14r2
阴影部分的面积为:4r2-3.14r2=0.86r2
如果两个圆的半径都是r,结果又是怎样的?
当r=1m时,和前面的计算结果完全一致。
一个三角形的面积为:
阴影部分的面积:3.14r2-2r2=1.14r2
正方形的面积为:2×r2=2r2
当圆的半径为r时,右图中:
答:左图中正方形与圆之间的面积是0.86 m2,
右图中圆与正方形之间的面积是1.14m2。
r
如果你仔细观察就会发现:我们周围很多东西的平面轮廓都是圆形的,如车轮、马路上的大多数井盖······这是为什么呢?
生活中的数学
车轮平面轮廓采用圆形,是利用同一圆的半径都相等的性质,把车轴装在车轮的圆心上。当车轮在地面上滚动的时候,车轴离地面的距离总是等于车轮的半径,因此只要道路平坦,车子就会平稳地在地面上行驶。试想一下,如果车轮是正方形的,为了保持车辆的平稳行驶,道路应该是什么样子的呢?
生活中的数学
井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,这里利用了同一圆的直径都相等的性质。
生活中的数学
1.下图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
(教材P70“做一做”)
03
学以致用
正方形的面积为:
24×(24÷2)÷2×2=288(cm2)
圆的面积为:3.14×(24÷2)2=452.16(cm2)
外面的圆与内部的正方形之间的面积为:
452.16-288=164.16(cm2)
答:外面的圆与内部的正方形之间的面积是164.16cm2。
2.下图中的铜钱直径28 mm,中间的正方形边长为6 mm。这个铜钱的面积是多少?
(教材P72“练习十五”第9题)
正方形的面积为:6×6=36(mm2)
圆的面积为:
3.14×(28÷2)2=615.44(mm2)
这个铜钱的面积为:615.44-36=579.44(mm2)
答:铜钱的面积为579.44mm2。
3.一个运动场如图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P73“练习十五”第10题)
C =2×C半圆+2×100 m
=2×3.14×32+2×100
=200.96+200
=400.96(米)
3.一个运动场如图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P73“练习十五”第10题)
S =2×S半圆+S长方形
=2×(3.14×322÷2)+(2×32)×100
=3215.36+6400
=9615.36(平方米)
答:这个运动场的周长是400.96米,面积是9615.36平方米。
4.一个圆的周长是62.8 m,半径增加了2 m后,面积增加了多少?
(教材P73“练习十五”第13题)
增加2 m后的半径变为:10+2=12(m)
圆的半径
半径增加后的面积为:3.14×122=452.16(m2)
答:面积增加了138.16m2。
增加之前的面积为:3.14×102=314(m2)
面积增加了:452.16-314 =138.16(m2)
04
课堂小结
“外圆内方,外方内圆”图形面积的计算
1.在“外方内圆”图形中,圆的直径等于正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2.在“外圆内方”图形中,这个正方形的对角线等于圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r 。
