2021-2022学年人教版九年级数学上册第25单元 概率初步 单元练习(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第25单元 概率初步 单元练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 153.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 15:53:21 | ||
图片预览




文档简介
第25单元
概率初步同步练习
一、选择题
1.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
2.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A.
B.
C.
D.
3.某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( )
A.
B.
C.
D.
4.某商店举办有奖销售活动,活动规则如下:凡购满100元者得奖券一张,每1000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个.那么,买100元商品的中奖概率是( )
A.
B.
C.
D.
5.转动下列名转盘,指针指向红色区域的概率最大的是( )
A.
B.
C.
D.
6.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( )
A.10粒
B.160粒
C.450粒
D.500粒
7.在某班举行的歌王争霸赛上,小孙、芳芳、阿玉报名参加了竞选,分A,B,C,D四组进行比赛,选手通过抽签方式参加比赛,则小孙、芳芳和阿玉分到同一组的概率为( )
A.
B.
C.
D.
8.下列说法正确的是( )
A.“明天降雨的概率为50%”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
二、填空题
9.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
10.如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
.
11.某口袋中有红色、黄色、蓝色玻璃球共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有
个.
12.一个袋子里有2个红色球,3个黄色球,4个绿色球,这些球除了颜色不同外,其他都相同.从袋子中随机地摸出一个球是红色或绿色的概率是
.
不透明的袋子中有三个小球,上面分别写着“﹣1、0、1”三个数字,除数字外无其他差别.从中随机摸出一个小球,把这个数字记为x,小球不放回,第二次再从袋子中摸出一个小球,这个数字记为y,则在平面直角坐标系中,点(x,y)恰好在直线y=x﹣1上的概率为
.
解答题
14.如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
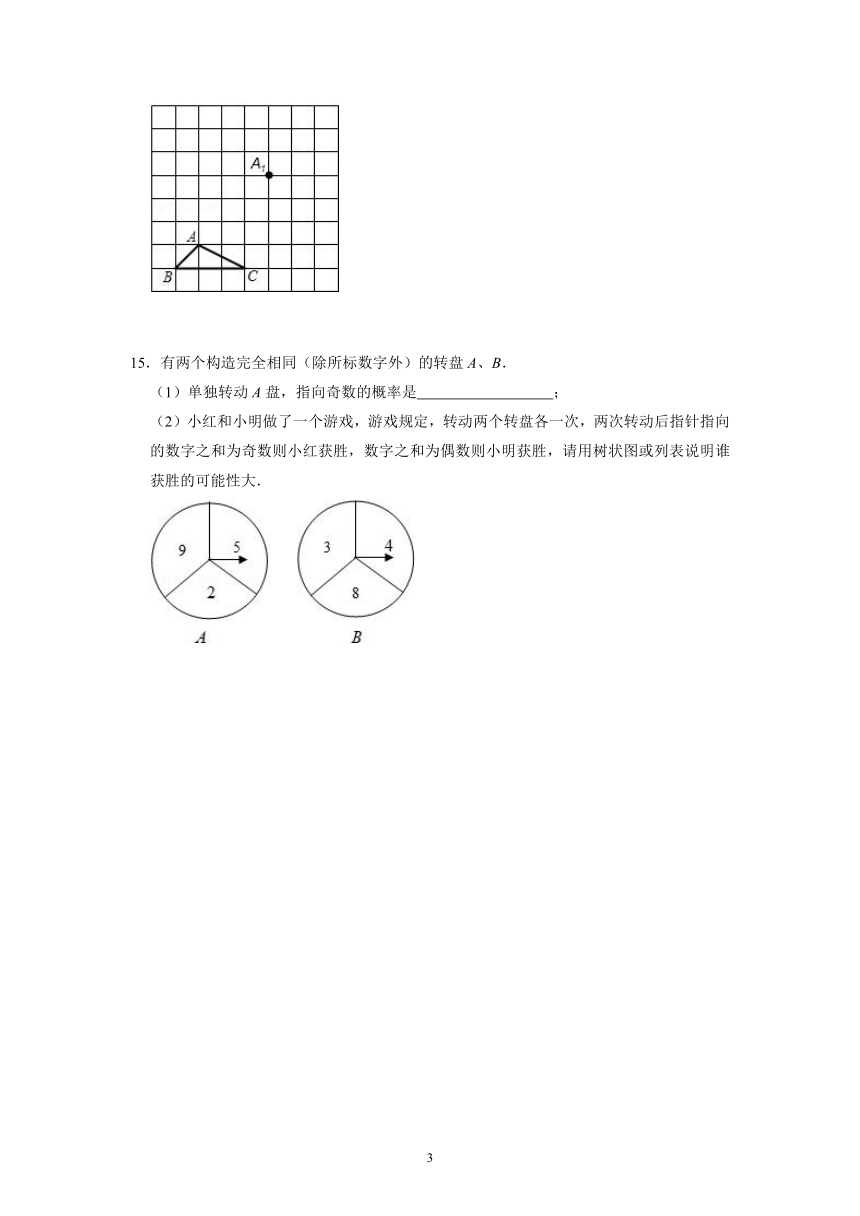
15.有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是
;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.
16.某中学为了解学生对新闻,体育,娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.
根据两图提供的信息,回答下列问题:
(1)本次调查了多少人?
(2)请补全条形统计图;
(3)在全班同学中,甲,乙,丙,丁等同学最喜欢体育类节目,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲,乙两同学的概率.
第25单元
概率初步同步练习参考答案与解析
一、选择题
1.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
【答案】A
【解答】解:A、从一个只有红球的盒子里摸出一个球是红球,是必然事件;
B、买一张电影票,座位号是5的倍数,是随机事件;
C、掷一枚质地均匀的硬币,正面向上,是随机事件;
D、走过一个红绿灯路口时,前方正好是红灯,是随机事件.
故选:A.
2.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A.
B.
C.
D.
【答案】A
【解答】解:∵任意掷一枚质地均匀的骰子,共有6种等可能的结果,且掷出的点数大于4的有2种情况,
∴任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是:=.
故选:A.
3.某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( )
B.
C.
D.
【答案】D
【解答】解:∵整个正方形被分成了9个小正方形,黑色正方形有5个,
∴落在黑色区域即获得笔记本的概率为,
故选:D
4.某商店举办有奖销售活动,活动规则如下:凡购满100元者得奖券一张,每1000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个.那么,买100元商品的中奖概率是( )
A.
B.
C.
D.
【答案】D
【解答】解:买100元商品的中奖的概率==.
故选:D.
5.转动下列名转盘,指针指向红色区域的概率最大的是( )
A.
B.
C.
D.
【答案】D
【解答】解:红色区域面积与圆的面积之比值即为指针指向红色区域的概率,观察可知红色区域面积D>C=A>B.故选:D.
6.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( )
A.10粒
B.160粒
C.450粒
D.500粒
【答案】C
【解答】解:设原黄豆数为x,则
染色黄豆的概率为
解得x=450.
故选:C.
7.下列说法正确的是( )
A.“明天降雨的概率为50%”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
【答案】D
【解答】解:A、明天降雨的概率是50%表示明天有可能降雨,此选项错误;
B、了解全国快递包裹产生的包装垃圾数量适合采用抽样调查方式,此选项错误;
C、掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是随机事件,此选项错误;
D、一组数据的方差越大,则这组数据的波动也越大,此选项正确;
故选:D.
8.在某班举行的歌王争霸赛上,小孙、芳芳、阿玉报名参加了竞选,分A,B,C,D四组进行比赛,选手通过抽签方式参加比赛,则小孙、芳芳和阿玉分到同一组的概率为( )
A.
B.
C.
D.
【答案】A
【解答】解:把A,B,C,D分别记为1,2,3,4,
画树状图如图:
共有64个等可能的结果,小孙、芳芳和阿玉分到同一组的结果有4个,
∴小孙、芳芳和阿玉分到同一组的概率为=,
故选:A.
二、填空题
9.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
【答案】
【解答】解:∵经过一个十字路口,共有红、黄、绿三色交通信号灯,
∴在路口遇到红灯、黄灯、绿灯的概率之和是1,
∵在路口遇到红灯的概率为,遇到黄灯的概率为,
∴遇到绿灯的概率为1﹣=;
故答案为:.
10.如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
.
【答案】
【解答】解:因为⊙O的直径为分米,则半径为分米,⊙O的面积为π()2=平方分米;
正方形的边长为=1分米,面积为1平方分米;
因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)==.
故答案为:.
某口袋中有红色、黄色、蓝色玻璃球共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有
个.
【答案】18
【解答】解:∵摸到红球、黄球、蓝球的频率为35%、25%和40%,
∴摸到黄球的概率为0.25,
故口袋中黄色玻璃球有0.25×72=18(个).
故答案为:18.
12.一个袋子里有2个红色球,3个黄色球,4个绿色球,这些球除了颜色不同外,其他都相同.从袋子中随机地摸出一个球是红色或绿色的概率是
.
【答案】
【解答】解:因为个袋子中装有2个红色球,3个黄色球,4个绿色球,
所以随机地从这个袋子中摸出一个球,摸到红色或绿色的概率为=.
故答案为:.
不透明的袋子中有三个小球,上面分别写着“﹣1、0、1”三个数字,除数字外无其他差别.从中随机摸出一个小球,把这个数字记为x,小球不放回,第二次再从袋子中摸出一个小球,这个数字记为y,则在平面直角坐标系中,点(x,y)恰好在直线y=x﹣1上的概率为
.
【答案】
【解答】解:列表如下,
﹣1
0
1
﹣1
(0,﹣1)
(1,﹣1)
0
(﹣1,0)
(1,0)
1
(﹣1,1)
(0,1)
由表可知,共有6种等可能结果,其中点(x,y)恰好在直线y=x﹣1上的有(0,﹣1)和(1,0)这2种结果,
所以点(x,y)恰好在直线y=x﹣1上的概率为=,
故答案为:.
解答题
14.如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
【答案】(1)看详解(2)看详解
(3)B所走的路径总长=
【解答】解:(1)连接AA1,然后从C点作AA1的平行线且AA1=CC1.
同理找到点B.
(2)画图如下:
(3)B经过(1)、(2)变换的路径如图红色部分所示:
,
弧B1B2的长=,
故点B所走的路径总长=.
15.有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是
;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.
【答案】(1)
(2)P(小红获胜)=,P(小明获胜)=
【解答】解:(1)∵单独转动A盘,共有3种情况,指向奇数的有2种情况,
∴单独转动A盘,指向奇数的概率是:;
故答案为:;
(2)画树状图得:
∵共有9种等可能的结果,两次转动后指针指向的数字之和为奇数的有5种情况,数字之和为偶数的有4种情况,
∴P(小红获胜)=,P(小明获胜)=.
16.某中学为了解学生对新闻,体育,娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.
根据两图提供的信息,回答下列问题:
(1)本次调查了多少人?
(2)请补全条形统计图;
(3)在全班同学中,甲,乙,丙,丁等同学最喜欢体育类节目,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲,乙两同学的概率.
【答案】(1)50人,(2)看解答
(3)甲、乙两位同学的概率为
【解答】解:(1)被调查的总人数为:9÷18%=50(人),
即本次调查了50人;
(2)喜欢娱乐的学生有50﹣6﹣15﹣9=20(人),
补全的条形统计图如右图所示;
(3)树状图如下图所示,
故恰好同时选中甲、乙两位同学的概率为.
(
2
)
概率初步同步练习
一、选择题
1.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
2.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A.
B.
C.
D.
3.某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( )
A.
B.
C.
D.
4.某商店举办有奖销售活动,活动规则如下:凡购满100元者得奖券一张,每1000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个.那么,买100元商品的中奖概率是( )
A.
B.
C.
D.
5.转动下列名转盘,指针指向红色区域的概率最大的是( )
A.
B.
C.
D.
6.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( )
A.10粒
B.160粒
C.450粒
D.500粒
7.在某班举行的歌王争霸赛上,小孙、芳芳、阿玉报名参加了竞选,分A,B,C,D四组进行比赛,选手通过抽签方式参加比赛,则小孙、芳芳和阿玉分到同一组的概率为( )
A.
B.
C.
D.
8.下列说法正确的是( )
A.“明天降雨的概率为50%”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
二、填空题
9.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
10.如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
.
11.某口袋中有红色、黄色、蓝色玻璃球共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有
个.
12.一个袋子里有2个红色球,3个黄色球,4个绿色球,这些球除了颜色不同外,其他都相同.从袋子中随机地摸出一个球是红色或绿色的概率是
.
不透明的袋子中有三个小球,上面分别写着“﹣1、0、1”三个数字,除数字外无其他差别.从中随机摸出一个小球,把这个数字记为x,小球不放回,第二次再从袋子中摸出一个小球,这个数字记为y,则在平面直角坐标系中,点(x,y)恰好在直线y=x﹣1上的概率为
.
解答题
14.如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
15.有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是
;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.
16.某中学为了解学生对新闻,体育,娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.
根据两图提供的信息,回答下列问题:
(1)本次调查了多少人?
(2)请补全条形统计图;
(3)在全班同学中,甲,乙,丙,丁等同学最喜欢体育类节目,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲,乙两同学的概率.
第25单元
概率初步同步练习参考答案与解析
一、选择题
1.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
【答案】A
【解答】解:A、从一个只有红球的盒子里摸出一个球是红球,是必然事件;
B、买一张电影票,座位号是5的倍数,是随机事件;
C、掷一枚质地均匀的硬币,正面向上,是随机事件;
D、走过一个红绿灯路口时,前方正好是红灯,是随机事件.
故选:A.
2.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A.
B.
C.
D.
【答案】A
【解答】解:∵任意掷一枚质地均匀的骰子,共有6种等可能的结果,且掷出的点数大于4的有2种情况,
∴任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是:=.
故选:A.
3.某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( )
B.
C.
D.
【答案】D
【解答】解:∵整个正方形被分成了9个小正方形,黑色正方形有5个,
∴落在黑色区域即获得笔记本的概率为,
故选:D
4.某商店举办有奖销售活动,活动规则如下:凡购满100元者得奖券一张,每1000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个.那么,买100元商品的中奖概率是( )
A.
B.
C.
D.
【答案】D
【解答】解:买100元商品的中奖的概率==.
故选:D.
5.转动下列名转盘,指针指向红色区域的概率最大的是( )
A.
B.
C.
D.
【答案】D
【解答】解:红色区域面积与圆的面积之比值即为指针指向红色区域的概率,观察可知红色区域面积D>C=A>B.故选:D.
6.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( )
A.10粒
B.160粒
C.450粒
D.500粒
【答案】C
【解答】解:设原黄豆数为x,则
染色黄豆的概率为
解得x=450.
故选:C.
7.下列说法正确的是( )
A.“明天降雨的概率为50%”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
【答案】D
【解答】解:A、明天降雨的概率是50%表示明天有可能降雨,此选项错误;
B、了解全国快递包裹产生的包装垃圾数量适合采用抽样调查方式,此选项错误;
C、掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是随机事件,此选项错误;
D、一组数据的方差越大,则这组数据的波动也越大,此选项正确;
故选:D.
8.在某班举行的歌王争霸赛上,小孙、芳芳、阿玉报名参加了竞选,分A,B,C,D四组进行比赛,选手通过抽签方式参加比赛,则小孙、芳芳和阿玉分到同一组的概率为( )
A.
B.
C.
D.
【答案】A
【解答】解:把A,B,C,D分别记为1,2,3,4,
画树状图如图:
共有64个等可能的结果,小孙、芳芳和阿玉分到同一组的结果有4个,
∴小孙、芳芳和阿玉分到同一组的概率为=,
故选:A.
二、填空题
9.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
【答案】
【解答】解:∵经过一个十字路口,共有红、黄、绿三色交通信号灯,
∴在路口遇到红灯、黄灯、绿灯的概率之和是1,
∵在路口遇到红灯的概率为,遇到黄灯的概率为,
∴遇到绿灯的概率为1﹣=;
故答案为:.
10.如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
.
【答案】
【解答】解:因为⊙O的直径为分米,则半径为分米,⊙O的面积为π()2=平方分米;
正方形的边长为=1分米,面积为1平方分米;
因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)==.
故答案为:.
某口袋中有红色、黄色、蓝色玻璃球共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有
个.
【答案】18
【解答】解:∵摸到红球、黄球、蓝球的频率为35%、25%和40%,
∴摸到黄球的概率为0.25,
故口袋中黄色玻璃球有0.25×72=18(个).
故答案为:18.
12.一个袋子里有2个红色球,3个黄色球,4个绿色球,这些球除了颜色不同外,其他都相同.从袋子中随机地摸出一个球是红色或绿色的概率是
.
【答案】
【解答】解:因为个袋子中装有2个红色球,3个黄色球,4个绿色球,
所以随机地从这个袋子中摸出一个球,摸到红色或绿色的概率为=.
故答案为:.
不透明的袋子中有三个小球,上面分别写着“﹣1、0、1”三个数字,除数字外无其他差别.从中随机摸出一个小球,把这个数字记为x,小球不放回,第二次再从袋子中摸出一个小球,这个数字记为y,则在平面直角坐标系中,点(x,y)恰好在直线y=x﹣1上的概率为
.
【答案】
【解答】解:列表如下,
﹣1
0
1
﹣1
(0,﹣1)
(1,﹣1)
0
(﹣1,0)
(1,0)
1
(﹣1,1)
(0,1)
由表可知,共有6种等可能结果,其中点(x,y)恰好在直线y=x﹣1上的有(0,﹣1)和(1,0)这2种结果,
所以点(x,y)恰好在直线y=x﹣1上的概率为=,
故答案为:.
解答题
14.如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
【答案】(1)看详解(2)看详解
(3)B所走的路径总长=
【解答】解:(1)连接AA1,然后从C点作AA1的平行线且AA1=CC1.
同理找到点B.
(2)画图如下:
(3)B经过(1)、(2)变换的路径如图红色部分所示:
,
弧B1B2的长=,
故点B所走的路径总长=.
15.有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是
;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.
【答案】(1)
(2)P(小红获胜)=,P(小明获胜)=
【解答】解:(1)∵单独转动A盘,共有3种情况,指向奇数的有2种情况,
∴单独转动A盘,指向奇数的概率是:;
故答案为:;
(2)画树状图得:
∵共有9种等可能的结果,两次转动后指针指向的数字之和为奇数的有5种情况,数字之和为偶数的有4种情况,
∴P(小红获胜)=,P(小明获胜)=.
16.某中学为了解学生对新闻,体育,娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.
根据两图提供的信息,回答下列问题:
(1)本次调查了多少人?
(2)请补全条形统计图;
(3)在全班同学中,甲,乙,丙,丁等同学最喜欢体育类节目,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲,乙两同学的概率.
【答案】(1)50人,(2)看解答
(3)甲、乙两位同学的概率为
【解答】解:(1)被调查的总人数为:9÷18%=50(人),
即本次调查了50人;
(2)喜欢娱乐的学生有50﹣6﹣15﹣9=20(人),
补全的条形统计图如右图所示;
(3)树状图如下图所示,
故恰好同时选中甲、乙两位同学的概率为.
(
2
)
同课章节目录
