人教版数学六年级上册5圆 解决问题 课件(16张PPT)
文档属性
| 名称 | 人教版数学六年级上册5圆 解决问题 课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 14:53:41 | ||
图片预览




文档简介
(共16张PPT)
第 7 课时 解决问题
圆
5
新课导入—探究新知—课堂检测—课堂小结—课后作业
人教版-数学-六年级上册
教学目标
1、运用圆的面积公式解决生活中的数学问题,结合具体情景认识与圆相结合的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
2、在解决实际问题的过程中,通过独立思考、合作探究、教讨论交流等活动,培养学生分析问题和解决问题的能力。
3、结合例题渗透传统文化的教育,使学生将数学和实际生活联系起来,感受数学的价值,提升学习的兴趣。
教学重难点:
1、理解并掌握“外方内圆” 和“外圆内方” 图形中圆和正方形面积的计算方法。
2、对组合图形进行分析。
新 课 导 入
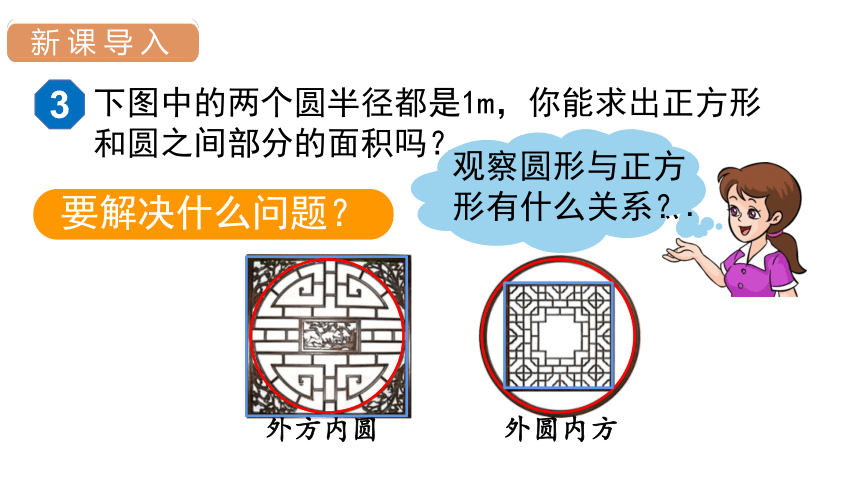
中国建筑、用品中经常能见到“外方内圆”和“外圆内方”的设计。
3
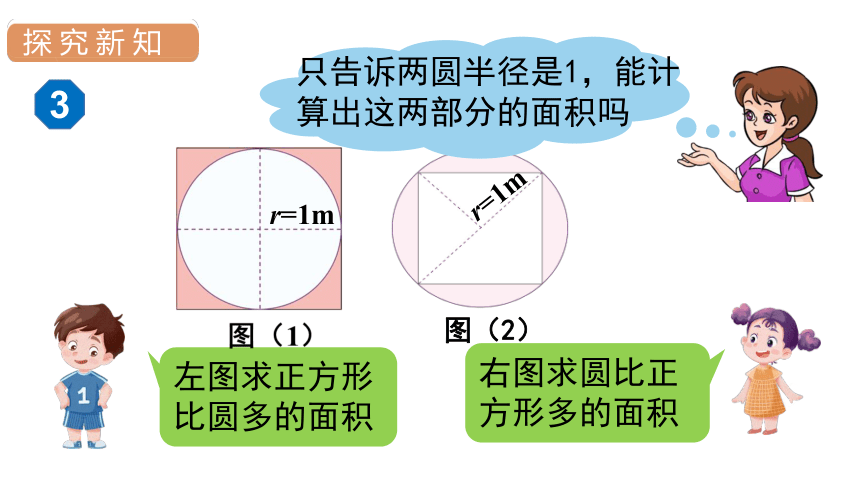
下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
要解决什么问题?
新 课 导 入
观察这两幅图,它们有什么特点?
外方内圆
外圆内方
观察圆形与正方形有什么关系?
3
探 究 新 知
左图求正方形比圆多的面积
r=1m
图(2)
r=1m
只告诉两圆半径是1,能计算出这两部分的面积吗
右图求圆比正方形多的面积
3
怎样解答?
探 究 新 知
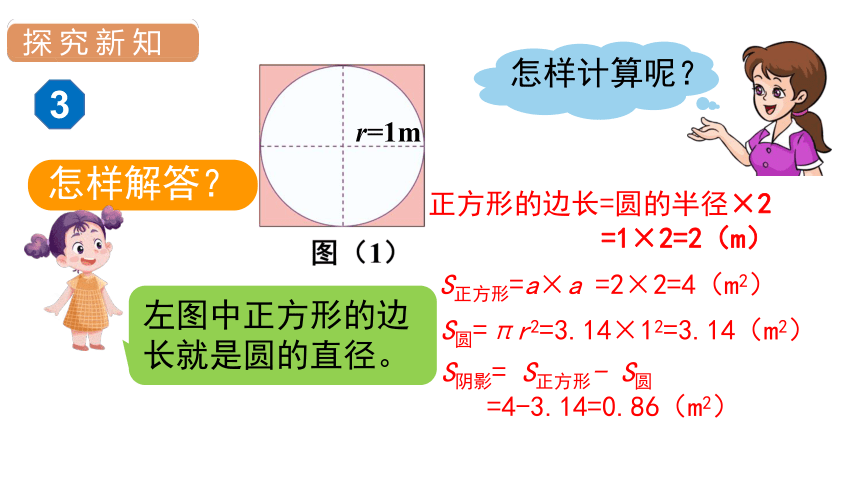
左图中正方形的边长就是圆的直径。
r=1m
怎样计算呢?
正方形的边长=圆的半径×2
=1×2=2(m)
S正方形=a×a =2×2=4(m2)
S圆=πr2=3.14×12=3.14(m2)
S阴影= S正方形- S圆
=4-3.14=0.86(m2)
3
怎样解答?
探 究 新 知
右图中正方形……。
观察三角形的底和高,有什么发现,正方形面积如何计算?
图(2)
r=1m
h
S正方形=圆的直径×半径
=2×1=2(m2)
S圆=πr2=3.14×12=3.14(m2)
S阴影=S圆- S正方形
=3.14-2=1.14(m2)
3
探 究 新 知
解答合理吗?
外方内圆面积差:
(2r) -3.14×r
=0.86r
外圆内方面积差:
3.14×r -(×2r×r)×2
=1.14r
如果两个圆的半径都是r,结果又是怎样的?
3
探 究 新 知
当r=1 m时,和前面的结果完全一致。
解答合理吗?
答:左图中正方形与圆之间的面积是0.86 m ,
右图中圆与正方形之间的面积是1.14 m 。
课 堂 检 测
1. 左图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
答:外面的圆与内部的正方形之间的面积约是164.16cm 。
=3.14 × 122--144 ×2
=3164.16 (cm2)
3.14×(24÷2)2-( ×24 ×12 ) × 2
(教材P70做一做)
课 堂 检 测
2、下图中的铜钱直径28mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
=3.14 × 142--36
=579.44 (mm2)
3.14×(28÷2)2-6×6
答:铜钱的面积是579.44mm 。
(教材P71T9)
课 堂 小 结
=S圆-S正
S外圆内方面积差
在正方形中画一个最大的圆,这个圆的直径等于正方形的边长,正方形和圆之间部分的面积都是0.86 r 倍,在圆内画一个最大的正方形,这个正方形的对角线就是圆的直径,正方形和圆之间部分的面积都是1.14 r 倍。
绿色圃中小学教育网http://www.lspjy.com
课 后 作 业
1、一个运动场如图,两段式半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米
C=2×3.14×32+100+×2
=200.96+200
=400.96(m)
(教材P72T10)
绿色圃中小学教育网http://www.lspjy.com
课 后 作 业
1、一个运动场如图,两段式半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米
S=3.14×322+100×(32×2)
=3215.36+6400
=9615.36(m2)
答:这个运动场的周长是400.96米,面积9615.36平方米。
课 后 作 业
2、土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”土楼的外围形状有圆形、方形、椭圆形等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是14m。两座土楼的房屋占地面积相差多少
S=S环1-S环2
=3.14×[(34÷2)2-(14÷2)2]
-3.14×[(26÷2)2-(14÷2)2]
=376.8(m2)
=3.14×(172-72 -132+72 )
=3.14×120
答:两座土楼的房屋占地面积相差376.8 m2
(教材P72T12)
谢谢
第 7 课时 解决问题
圆
5
新课导入—探究新知—课堂检测—课堂小结—课后作业
人教版-数学-六年级上册
教学目标
1、运用圆的面积公式解决生活中的数学问题,结合具体情景认识与圆相结合的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
2、在解决实际问题的过程中,通过独立思考、合作探究、教讨论交流等活动,培养学生分析问题和解决问题的能力。
3、结合例题渗透传统文化的教育,使学生将数学和实际生活联系起来,感受数学的价值,提升学习的兴趣。
教学重难点:
1、理解并掌握“外方内圆” 和“外圆内方” 图形中圆和正方形面积的计算方法。
2、对组合图形进行分析。
新 课 导 入
中国建筑、用品中经常能见到“外方内圆”和“外圆内方”的设计。
3
下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
要解决什么问题?
新 课 导 入
观察这两幅图,它们有什么特点?
外方内圆
外圆内方
观察圆形与正方形有什么关系?
3
探 究 新 知
左图求正方形比圆多的面积
r=1m
图(2)
r=1m
只告诉两圆半径是1,能计算出这两部分的面积吗
右图求圆比正方形多的面积
3
怎样解答?
探 究 新 知
左图中正方形的边长就是圆的直径。
r=1m
怎样计算呢?
正方形的边长=圆的半径×2
=1×2=2(m)
S正方形=a×a =2×2=4(m2)
S圆=πr2=3.14×12=3.14(m2)
S阴影= S正方形- S圆
=4-3.14=0.86(m2)
3
怎样解答?
探 究 新 知
右图中正方形……。
观察三角形的底和高,有什么发现,正方形面积如何计算?
图(2)
r=1m
h
S正方形=圆的直径×半径
=2×1=2(m2)
S圆=πr2=3.14×12=3.14(m2)
S阴影=S圆- S正方形
=3.14-2=1.14(m2)
3
探 究 新 知
解答合理吗?
外方内圆面积差:
(2r) -3.14×r
=0.86r
外圆内方面积差:
3.14×r -(×2r×r)×2
=1.14r
如果两个圆的半径都是r,结果又是怎样的?
3
探 究 新 知
当r=1 m时,和前面的结果完全一致。
解答合理吗?
答:左图中正方形与圆之间的面积是0.86 m ,
右图中圆与正方形之间的面积是1.14 m 。
课 堂 检 测
1. 左图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
答:外面的圆与内部的正方形之间的面积约是164.16cm 。
=3.14 × 122--144 ×2
=3164.16 (cm2)
3.14×(24÷2)2-( ×24 ×12 ) × 2
(教材P70做一做)
课 堂 检 测
2、下图中的铜钱直径28mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
=3.14 × 142--36
=579.44 (mm2)
3.14×(28÷2)2-6×6
答:铜钱的面积是579.44mm 。
(教材P71T9)
课 堂 小 结
=S圆-S正
S外圆内方面积差
在正方形中画一个最大的圆,这个圆的直径等于正方形的边长,正方形和圆之间部分的面积都是0.86 r 倍,在圆内画一个最大的正方形,这个正方形的对角线就是圆的直径,正方形和圆之间部分的面积都是1.14 r 倍。
绿色圃中小学教育网http://www.lspjy.com
课 后 作 业
1、一个运动场如图,两段式半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米
C=2×3.14×32+100+×2
=200.96+200
=400.96(m)
(教材P72T10)
绿色圃中小学教育网http://www.lspjy.com
课 后 作 业
1、一个运动场如图,两段式半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米
S=3.14×322+100×(32×2)
=3215.36+6400
=9615.36(m2)
答:这个运动场的周长是400.96米,面积9615.36平方米。
课 后 作 业
2、土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”土楼的外围形状有圆形、方形、椭圆形等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是14m。两座土楼的房屋占地面积相差多少
S=S环1-S环2
=3.14×[(34÷2)2-(14÷2)2]
-3.14×[(26÷2)2-(14÷2)2]
=376.8(m2)
=3.14×(172-72 -132+72 )
=3.14×120
答:两座土楼的房屋占地面积相差376.8 m2
(教材P72T12)
谢谢
