华东师大版七上数学 5.1.1对顶角课件(22张)
文档属性
| 名称 | 华东师大版七上数学 5.1.1对顶角课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
补角的性质
同角
的补角相等
或等角
同角或等角的余角相等
余角的性质
第五章:相交线与平行线
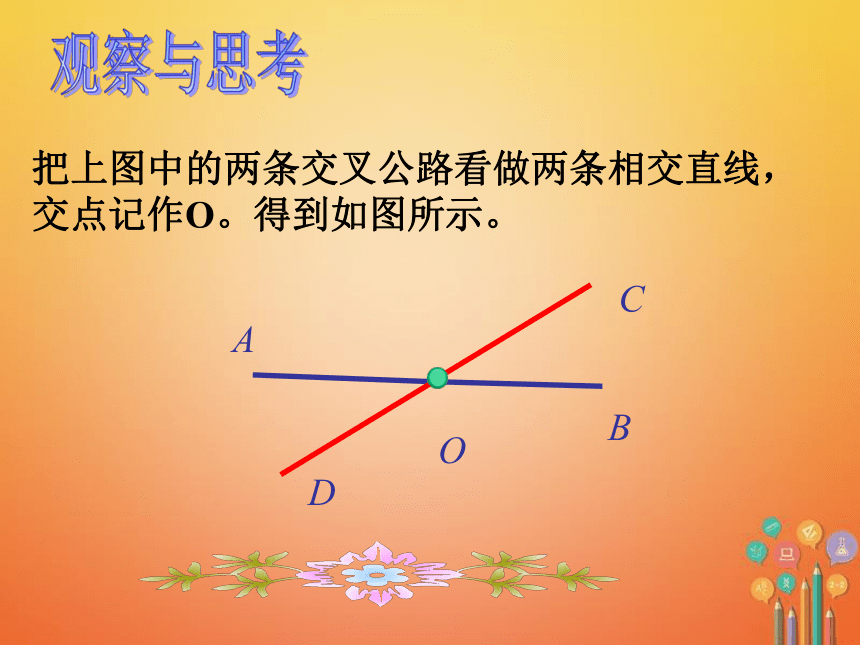
把上图中的两条交叉公路看做两条相交直线,交点记作O。得到如图所示。
A
B
D
C
O
(3)观察∠AOD和∠BOC,它们的两边有什么特点?∠AOC和∠BOD呢?
(1)不计平角和周角,图中共有几个角?分别是什么?
(2)观察这些角的顶点,它们有什么特点?
四个角
∠AOD,∠BOC,∠AOC和∠BOD
四个角有公共的顶点O
∠AOD和∠BOC,它们的两边分别互为反向延长线,∠AOC和∠BOD也是它们的两边分别互为反向延长线。
(1)它们都是 相交形成的角;
(2)它们分别有 的顶点;
(3)其中一个角的两边分别是另一个角的 。
注意:符合这三个条件时,才能确定这两个角是对顶角,缺一个条件都不行。对顶角是成对存在的,它们互为对顶角,如∠AOD是∠BOC的对顶角,同时,∠BOC是∠AOD的对顶角,也常说∠AOD和∠BOC是对顶角。
对顶角的基本图形可以简单的记为x型。
对顶角
两条直线
公共
反向延长线
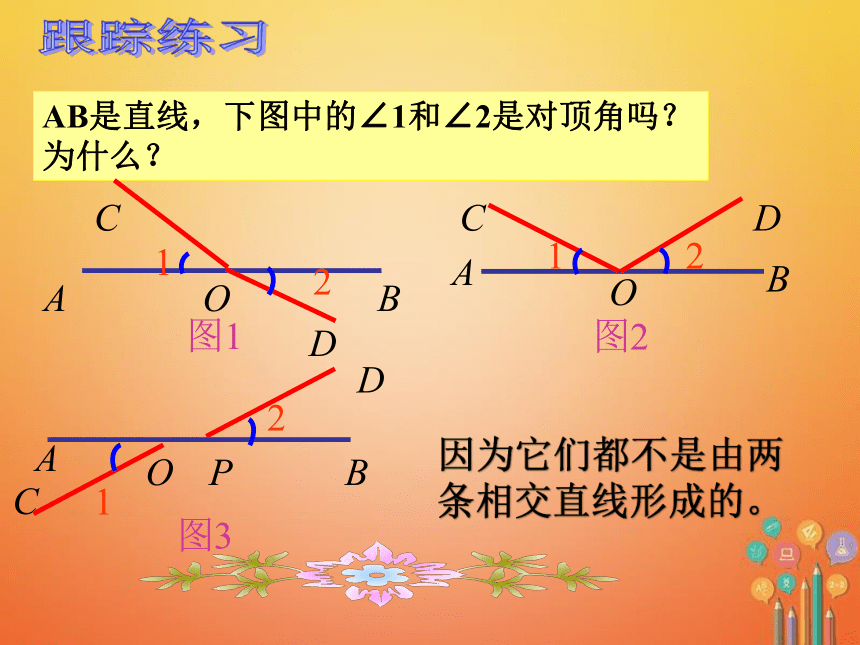
AB是直线,下图中的∠1和∠2是对顶角吗?为什么?
2
1
图1
A
B
C
D
O
2
1
图2
A
B
C
D
O
1
图3
2
A
B
D
C
P
O
因为它们都不是由两条相交直线形成的。
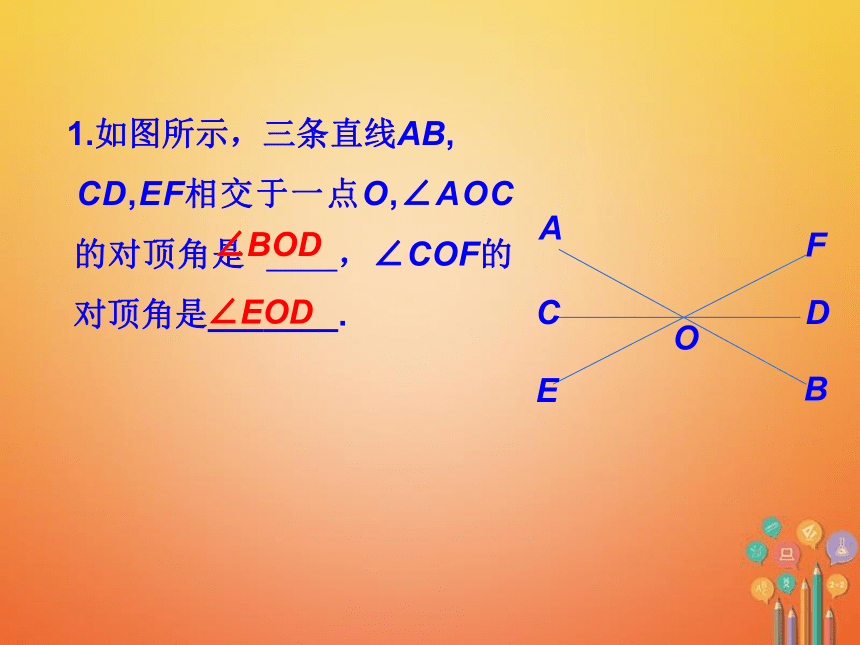
1.如图所示,三条直线AB,
CD,EF相交于一点O,∠AOC的对顶角是
,∠COF的对顶角是_______.
A
B
C
D
E
F
O
∠BOD
∠EOD
动手并思考:
用量角器量一量课本P160页图5.1.2中∠1和∠3的度数,并比较它们的大小关系?你能说明具有这种关系的道理吗?
如图,由∠1+∠2=180°,
∠2+∠3=180°,
可得∠1=∠3.
A
O
C
B
D
1
3
2
4
例1
已知:直线a,b相交,∠1=30°.求∠2,∠3,∠4的度数?
a
b
1
2
3
4
解:∠2=180°-∠1=180°-30°=150°,
∠3=180°-∠2=180°-150°=30°,
∠4=180°-∠1=180°-30°=150°,
由此,我们得到∠1=∠3,∠2=∠4.
对顶角相等
若∠2是∠1的3倍,求∠3的度数.
a
b
1
2
3
4
解:
设∠1=x,则∠2=3x.
因为∠2+∠1=180°,
所以3x+x=180°,
解得
x=45°,
所以∠3=∠1=
45°(对顶角相等).
跟踪训练
解:因为∠COB与∠AOD是对顶角,所以∠COB=∠AOD=110°。
∠AOC=∠COD-∠AOD=180°-110°=70°。
因为∠BOD与∠AOC是对顶角,所以∠BOD=∠AOC=70°。
由OE平分∠BOD,得∠BOE=∠EOD=
∠BOD=
x70°=35°。
如图,
直线AB和CD相交于点O,射线OE是∠BOD
的角平分线,已知∠AOD=110°,
求∠COB,∠AOC,
∠BOE,∠EOD的度数。
对顶角
对顶角
补角
角的平分线
∠COB
∠DOF
∠DOE
75°
2.要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
通过本节课的学习,你收获到什么?
对顶角的概念:
对顶角的性质:
对顶角的性质的应用:
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
补角的性质
同角
的补角相等
或等角
同角或等角的余角相等
余角的性质
第五章:相交线与平行线
把上图中的两条交叉公路看做两条相交直线,交点记作O。得到如图所示。
A
B
D
C
O
(3)观察∠AOD和∠BOC,它们的两边有什么特点?∠AOC和∠BOD呢?
(1)不计平角和周角,图中共有几个角?分别是什么?
(2)观察这些角的顶点,它们有什么特点?
四个角
∠AOD,∠BOC,∠AOC和∠BOD
四个角有公共的顶点O
∠AOD和∠BOC,它们的两边分别互为反向延长线,∠AOC和∠BOD也是它们的两边分别互为反向延长线。
(1)它们都是 相交形成的角;
(2)它们分别有 的顶点;
(3)其中一个角的两边分别是另一个角的 。
注意:符合这三个条件时,才能确定这两个角是对顶角,缺一个条件都不行。对顶角是成对存在的,它们互为对顶角,如∠AOD是∠BOC的对顶角,同时,∠BOC是∠AOD的对顶角,也常说∠AOD和∠BOC是对顶角。
对顶角的基本图形可以简单的记为x型。
对顶角
两条直线
公共
反向延长线
AB是直线,下图中的∠1和∠2是对顶角吗?为什么?
2
1
图1
A
B
C
D
O
2
1
图2
A
B
C
D
O
1
图3
2
A
B
D
C
P
O
因为它们都不是由两条相交直线形成的。
1.如图所示,三条直线AB,
CD,EF相交于一点O,∠AOC的对顶角是
,∠COF的对顶角是_______.
A
B
C
D
E
F
O
∠BOD
∠EOD
动手并思考:
用量角器量一量课本P160页图5.1.2中∠1和∠3的度数,并比较它们的大小关系?你能说明具有这种关系的道理吗?
如图,由∠1+∠2=180°,
∠2+∠3=180°,
可得∠1=∠3.
A
O
C
B
D
1
3
2
4
例1
已知:直线a,b相交,∠1=30°.求∠2,∠3,∠4的度数?
a
b
1
2
3
4
解:∠2=180°-∠1=180°-30°=150°,
∠3=180°-∠2=180°-150°=30°,
∠4=180°-∠1=180°-30°=150°,
由此,我们得到∠1=∠3,∠2=∠4.
对顶角相等
若∠2是∠1的3倍,求∠3的度数.
a
b
1
2
3
4
解:
设∠1=x,则∠2=3x.
因为∠2+∠1=180°,
所以3x+x=180°,
解得
x=45°,
所以∠3=∠1=
45°(对顶角相等).
跟踪训练
解:因为∠COB与∠AOD是对顶角,所以∠COB=∠AOD=110°。
∠AOC=∠COD-∠AOD=180°-110°=70°。
因为∠BOD与∠AOC是对顶角,所以∠BOD=∠AOC=70°。
由OE平分∠BOD,得∠BOE=∠EOD=
∠BOD=
x70°=35°。
如图,
直线AB和CD相交于点O,射线OE是∠BOD
的角平分线,已知∠AOD=110°,
求∠COB,∠AOC,
∠BOE,∠EOD的度数。
对顶角
对顶角
补角
角的平分线
∠COB
∠DOF
∠DOE
75°
2.要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
通过本节课的学习,你收获到什么?
对顶角的概念:
对顶角的性质:
对顶角的性质的应用:
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
