人教版2021年八年级上册:12.1 全等三角形 同步练习卷 (Word版含解析)
文档属性
| 名称 | 人教版2021年八年级上册:12.1 全等三角形 同步练习卷 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 18:32:14 | ||
图片预览

文档简介
人教版2021年八年级上册:12.1
全等三角形
同步练习卷
一.选择题
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47°
B.49°
C.84°
D.96°
2.如图,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是( )
A.80°
B.90°
C.100°
D.120°
3.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )
A.60°
B.100°
C.120°
D.135°
4.如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
5.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
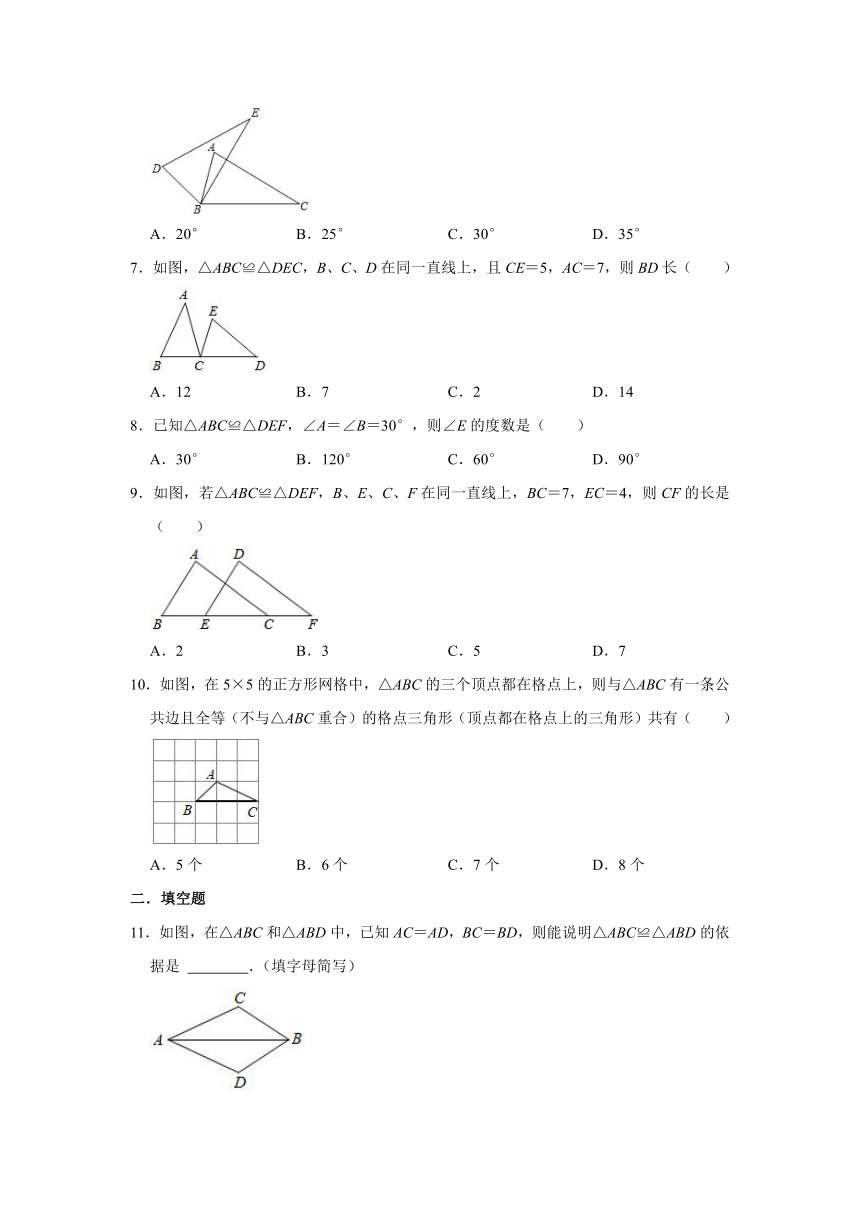
6.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20°
B.25°
C.30°
D.35°
7.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12
B.7
C.2
D.14
8.已知△ABC≌△DEF,∠A=∠B=30°,则∠E的度数是( )
A.30°
B.120°
C.60°
D.90°
9.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
10.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有( )
A.5个
B.6个
C.7个
D.8个
二.填空题
11.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是
.(填字母简写)
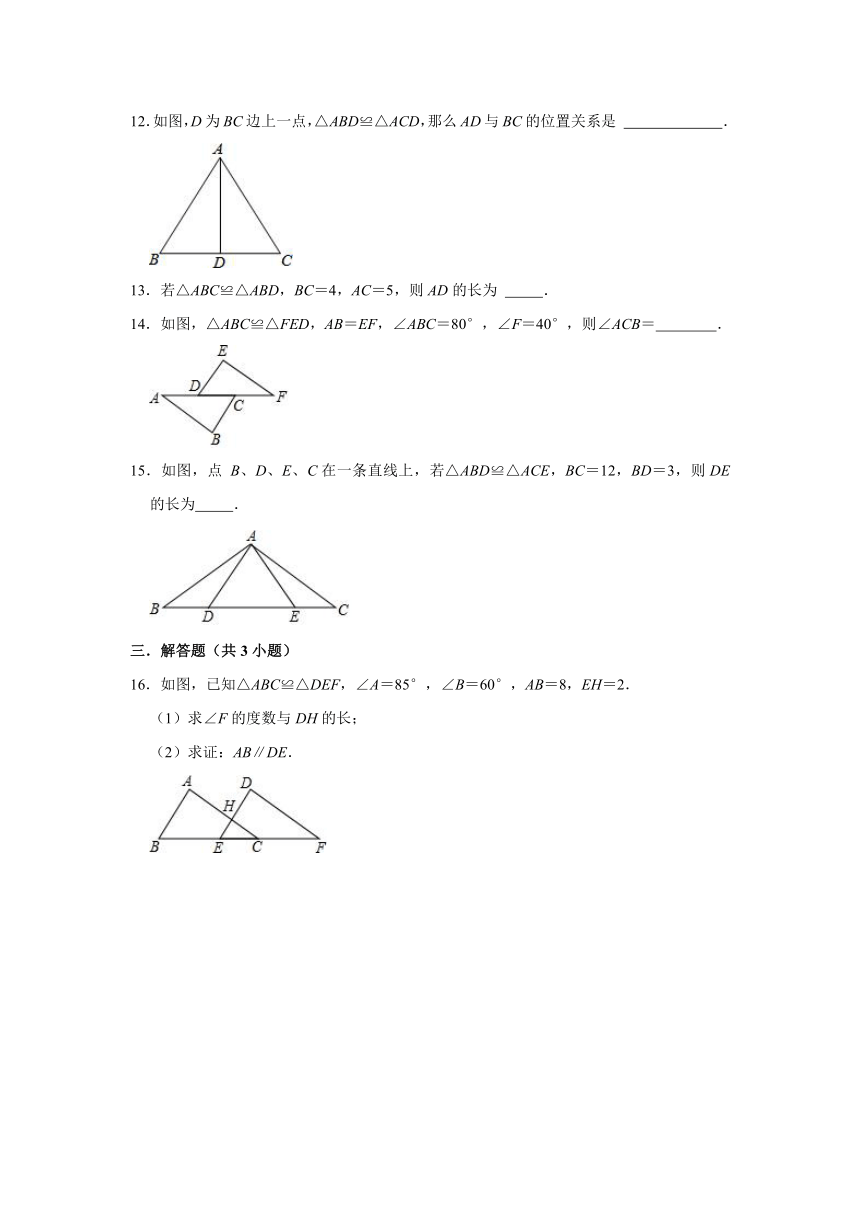
12.如图,D为BC边上一点,△ABD≌△ACD,那么AD与BC的位置关系是
.
13.若△ABC≌△ABD,BC=4,AC=5,则AD的长为
.
14.如图,△ABC≌△FED,AB=EF,∠ABC=80°,∠F=40°,则∠ACB=
.
15.如图,点
B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为
.
三.解答题(共3小题)
16.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
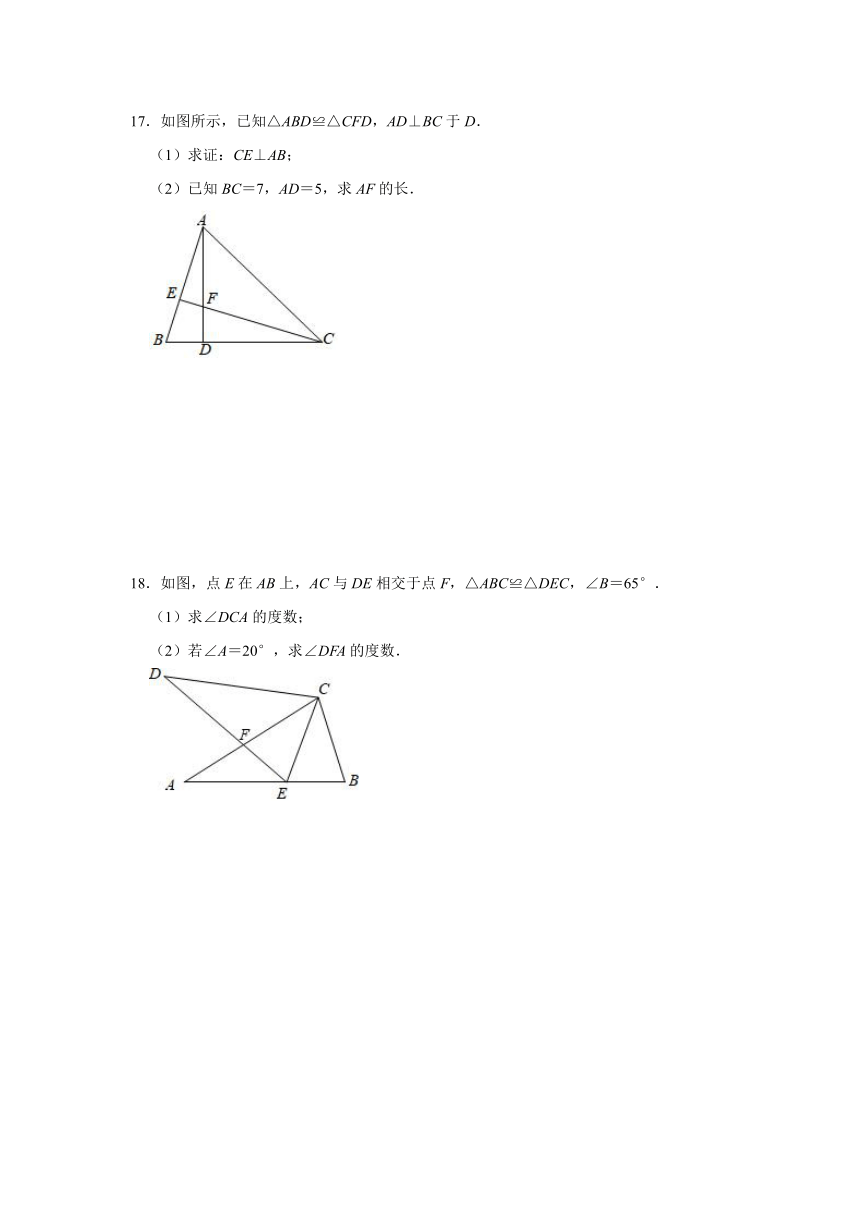
17.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
18.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:根据三角形内角和定理可得,∠2=180°﹣49°﹣47°=84°.
∵如图是两个全等三角形,
∴∠1=∠2=84°.
故选:C.
2.解:∵△ABC≌△ADC,
∴∠B=∠D,
∵∠B+∠D=160°,
∴∠B=80°,
故选:A.
3.解:∵△ABC≌△A'B'C',∠C'=24°,
∴∠C=∠C'=24°,
∴∠B=180°﹣∠A﹣∠C=180°﹣36°﹣24°=120°,
故选:C.
4.解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
5.解:∵△ABC≌△DEC,∠B=∠CEB=65°,
∴∠DEC=∠B=65°,
∴∠AEF=180°﹣65°﹣65°=50°,
∴∠DFA=∠A+∠AEF=20°+50°=70°,
故选:B.
6.解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
7.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
8.解:∵△ABC≌△DEF,∠A=∠B=30°,
∴∠D=∠E=∠A=∠B=30°,
则∠E的度数是30°.
故选:A.
9.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
10.解:如图所示,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出△ABG,△ABM,△ABH三个三角形和原三角形全等.
以AC为公共边不可以画出一个三角形和原三角形全等,
所以可画出6个.
故选:B.
二.填空题
11.解:在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS).
故答案为SSS.
12.解:AD垂直平分BC,
理由:∵△ABD≌△ACD,
∴∠ADB=∠ADC,BD=CD,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD垂直平分BC.
故答案为:AD垂直平分BC.
13.解:∵△ABC≌△ABD,AC=5,
∴AD=AC=5,
故答案为:5.
14.解:∵△ABC≌△FED,∠ABC=80°,∠F=40°,
∴∠ABC=∠FED=80°,∠A=∠F=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
故答案为:60°.
15.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
三.解答题(共3小题)
16.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
17.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
18.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
全等三角形
同步练习卷
一.选择题
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47°
B.49°
C.84°
D.96°
2.如图,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是( )
A.80°
B.90°
C.100°
D.120°
3.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )
A.60°
B.100°
C.120°
D.135°
4.如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
5.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
6.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20°
B.25°
C.30°
D.35°
7.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12
B.7
C.2
D.14
8.已知△ABC≌△DEF,∠A=∠B=30°,则∠E的度数是( )
A.30°
B.120°
C.60°
D.90°
9.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
10.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有( )
A.5个
B.6个
C.7个
D.8个
二.填空题
11.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是
.(填字母简写)
12.如图,D为BC边上一点,△ABD≌△ACD,那么AD与BC的位置关系是
.
13.若△ABC≌△ABD,BC=4,AC=5,则AD的长为
.
14.如图,△ABC≌△FED,AB=EF,∠ABC=80°,∠F=40°,则∠ACB=
.
15.如图,点
B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为
.
三.解答题(共3小题)
16.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
17.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
18.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:根据三角形内角和定理可得,∠2=180°﹣49°﹣47°=84°.
∵如图是两个全等三角形,
∴∠1=∠2=84°.
故选:C.
2.解:∵△ABC≌△ADC,
∴∠B=∠D,
∵∠B+∠D=160°,
∴∠B=80°,
故选:A.
3.解:∵△ABC≌△A'B'C',∠C'=24°,
∴∠C=∠C'=24°,
∴∠B=180°﹣∠A﹣∠C=180°﹣36°﹣24°=120°,
故选:C.
4.解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
5.解:∵△ABC≌△DEC,∠B=∠CEB=65°,
∴∠DEC=∠B=65°,
∴∠AEF=180°﹣65°﹣65°=50°,
∴∠DFA=∠A+∠AEF=20°+50°=70°,
故选:B.
6.解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
7.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
8.解:∵△ABC≌△DEF,∠A=∠B=30°,
∴∠D=∠E=∠A=∠B=30°,
则∠E的度数是30°.
故选:A.
9.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
10.解:如图所示,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出△ABG,△ABM,△ABH三个三角形和原三角形全等.
以AC为公共边不可以画出一个三角形和原三角形全等,
所以可画出6个.
故选:B.
二.填空题
11.解:在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS).
故答案为SSS.
12.解:AD垂直平分BC,
理由:∵△ABD≌△ACD,
∴∠ADB=∠ADC,BD=CD,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD垂直平分BC.
故答案为:AD垂直平分BC.
13.解:∵△ABC≌△ABD,AC=5,
∴AD=AC=5,
故答案为:5.
14.解:∵△ABC≌△FED,∠ABC=80°,∠F=40°,
∴∠ABC=∠FED=80°,∠A=∠F=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
故答案为:60°.
15.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
三.解答题(共3小题)
16.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
17.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
18.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
