河南省渑池县高中2021-2022学年高一上学期9月月考数学试题(Word版含答案)
文档属性
| 名称 | 河南省渑池县高中2021-2022学年高一上学期9月月考数学试题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览





文档简介
渑池高中2021-2022学年高一上学期9月数学月考试卷
一、单选题
1.已知函数
,若
在区间
上的最大值为
,则
的最小值是(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
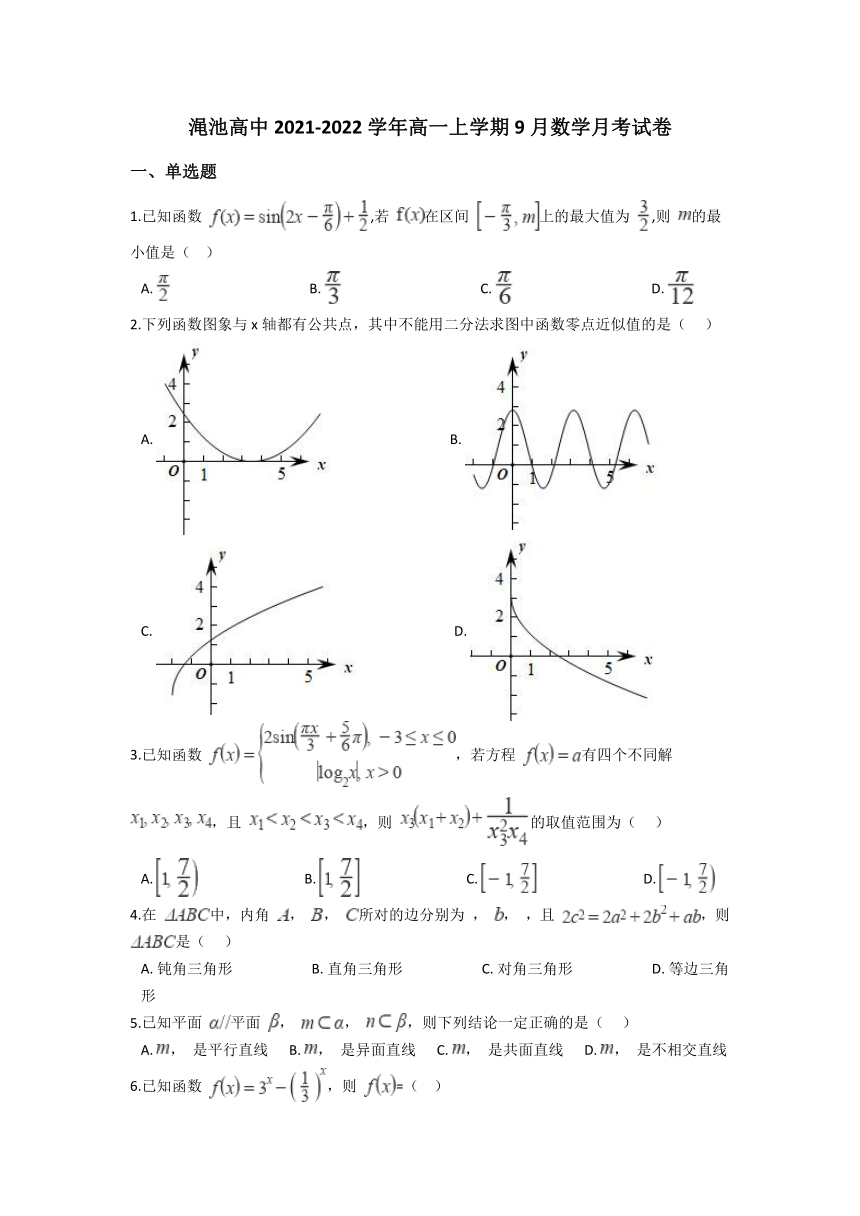
2.下列函数图象与x轴都有公共点,其中不能用二分法求图中函数零点近似值的是(???
)
A.????????????????????????????????B.?
C.????????????????????????????D.?
3.已知函数
,若方程
有四个不同解
,且
,则
的取值范围为(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
4.在
中,内角
,
,
所对的边分别为
,
,
,且
,则
是(???
)
A.?钝角三角形???????????????????????B.?直角三角形???????????????????????C.?对角三角形???????????????????????D.?等边三角形
5.已知平面
平面
,
,
,则下列结论一定正确的是(???
)
A.?,
是平行直线??????B.?,
是异面直线??????C.?,
是共面直线??????D.?,
是不相交直线
6.已知函数
,则
=(
??)
A.?是奇函数,且在R上是增函数??????????????????????????????B.?是偶函数,且在R上是增函数
C.?是奇函数,且在R上是减函数??????????????????????????????D.?是偶函数,且在R上是减函数
7.在
中,A最大,C最小,且
,
,则此三角形的三边之比为(???
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
8.已知函数
的值域为
,则实数
的取值范围是(??
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
9.设
,若3是
与
的等比中项,则
的最小值为(??
).
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
10.已知集合
,
,若
,则
的取值范围是(?
??)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
11.(?
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
12.若
,以下选项能推出
的是(?
)
A.??????????????????B.??????????????????C.??????????????????D.?
13.设奇函数f(x)满足:①f(x)在(0,+∞)上单调递增;②f(1)=0,则不等式(x+1)f(x)>0的解集为(?
)
A.?(-∞,-1)∪(1,+∞)?????????B.?(0,1)?????????C.?(-∞,-1)?????????D.?(-∞,-1)∪(-1,0)∪(1,+∞)
14.对任意
,函数
在区间
上不是单调函数,则实数
的取值范围是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
15.在锐角三角形△ABC中,a,b,c分别是角A,B,C的对边,(a+b+c)(a+c﹣b)=
,则cosA+sinC的取值范围为(??
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
16.已知函数
是定义域为
的偶函数,且其图象关于直线
对称,若当
时,
,则
的零点的个数为(???
)
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
17.已知等差数列
的前
项和
有最大值,且
,则满足
的最大正整数
的值为(??
)
A.?6??????????????????????????????????????????B.?7??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
18.已知
,若函数
有三个零点,则实数
的取值范围是(
??)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
19.已知二次函数
交
轴于
两点(
不重合),交
轴于
点.
圆
过
三点.下列说法正确的是(?
)
①
圆心
在直线
上;②
的取值范围是
;③
圆
半径的最小值为
;④
存在定点
,使得圆
恒过点
.
A.?①②③??????????????????????????????????B.?①③④??????????????????????????????????C.?②③??????????????????????????????????D.?①④
20.设
,则关于
的不等式
的解集是(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
二、填空题
21.已知
,
,则
________.
22.设函数g(x)=ex+ae-x(x∈R)是奇函数,则实数a=________.
23.已知集合
,
,若
,则
________.
24.在R上定义运算?:x?y=x(1﹣y),若不等式(x﹣a)?(x+a)<1对任意的实数x成立,则a的取值范围是________.
25.函数y=2﹣x﹣
(x>0)的值域为________.
26.已知等比数列
的公比为q,关于x的不等式
有下列说法:
①当
吋,不等式的解集
②当
吋,不等式的解集为
③当
>0吋,存在公比q,使得不等式解集为
④存在公比q,使得不等式解集为R.
上述说法正确的序号是________.
27.如图,设圆M的半径为2,点C是圆M上的定点,A,B是圆M上的两个动点,则
的最小值是________.
28.已知函数
,则
________.
29.已知函数
(
)的图像经过点
,函数
的图像经过点
,则
________.
30.当
取到最大值时,
________.
三、解答题
31..已知A,B,C为锐角△ABC的内角,
=(sinA,sinBsinC),
=(1,﹣2),
⊥
.
(1).tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2).求tanAtanBtanC的最小值.
32.已知三棱柱
中,四边形
为矩形.
(1)记平面
与平面
的交线为,求证:
平面
;
(2)若
,求证:
.
33.已知幂函数f(x)=x(m2+m)-1(m∈N
),经过点(2,
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
34.在
中,角A
,
B
,
C所对的边分别为a
,
b
,
c
,
且
.
(1)求角A;
(2)若
的外接圆半径为2,求
周长的最大值.
35.解关于x的不等式
.
36.如图,一座山其高
为
,一辆汽车在一条水平的公路上沿直线从
往
匀速行驶,在
处测得山顶
的仰角为
,经过
后汽车到达
处,这时测得山顶
的仰角为
,且
.
(1)求这辆汽车的速度;
(2)若汽车从
往
行驶5秒时到达
处,求此时山顶
与汽车的距离
.
37..已知
(1).求
的值;
(2).求
的值.
38..已知
是定义在R上的奇函数,当
时,
.
(1).求函数
的表达式;
(2).若函数
在区间
上是单调的,试确定a的取值范围.
39..已知点
,求
的边
上的中线所在的直线方程。
40.在迎来中国共产党成立100周年的重要时刻,我国脱贫攻坚战取得全面胜利,创造了又一个彪炳史册的人间奇迹.习近平总书记指出:“脱贫摘帽不是终点,而是新生活?新奋斗的起点.”为了解脱贫家庭人均年纯收入情况,某扶贫工作组对
两个地区2019年脱贫家庭进行简单随机抽样,共抽取600户家庭作为样本,获得数据如下表:
A地区
B地区
2019年人均年纯收入超过1万元
120户
200户
2019年人均年纯收入未超过1万元
180户
100户
假设所有脱贫家庭的人均年纯收入是否超过1万元相互独立.
(1)分别从A地区和B地区2019年脱贫家庭中各随机抽取1户,记X为这2户家庭中2019年人均年纯收入超过1万元的户数,且把频率视作概率.求
的分布列和数学期望;
(2)从样本中A地区的300户脱贫家庭中随机抽取4户,发现这4户家庭2020年人均年纯收入都超过1万元.根据这个结果,能否认为样本中A地区2020年人均年纯收入超过1万元的户数相比2019年有变化?请说明理由.????
参考数据:
.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
A
3.【答案】
A
4.【答案】
A
5.【答案】
D
6.【答案】
A
7.【答案】
B
8.【答案】
D
9.【答案】
C
10.【答案】
A
11.【答案】
B
12.【答案】
C
13.【答案】
D
14.【答案】
A
15.【答案】
B
16.【答案】
C
17.【答案】
C
18.【答案】
A
19.【答案】
D
20.【答案】
D
二、填空题
21.【答案】
-28
22.【答案】
-1
23.【答案】
24.【答案】
25.【答案】(﹣∞,﹣2]
26.【答案】
③
27.【答案】
-2
28.【答案】
4
29.【答案】
,
.
30.【答案】
三、解答题
31.【答案】
(1)解:依题意有sinA=2sinBsinC.
在△ABC中,A=π﹣B﹣C,
所以sinA=sin(B+C)=sinBcosC+cosBsinC,
所以2sinBsinC=sinBcosC+cosBsinC.
因为△ABC为锐角三角形,所以cosB>0,cosC>0,
所以tanB+tanC=2tanBtanC,
所以tanB,tanBtanC,tanC成等差数列
(2)解:在锐角△ABC中,
tanA=tan(π﹣B﹣C)=﹣tan(B+C)=﹣
,
即tanAtanBtanC=tanA+tanB+tanC,
由(1)知tanB+tanC=2tanBtanC,
于是tanAtanBtanC=tanA+2tanBtanC≥
,
整理得tanAtanBtanC≥8,
当且仅当tanA=4时取等号,
故tanAtanBtanC的最小值为8
32.【答案】
(1)证明:由棱柱的性质得
,
∵
平面
,
平面
,∴
平面
,
∵
平面
,平面
与平面
的交线为,
∴
,
∵
平面
,
平面
,
∴
平面
.
(2)作
在
所在平面的投影于点
,延长
,
,
,交边长
、
、
于点
、
、
,
∵
,
,所以
,
∵
,
,
、
平面
,
∴
平面
,
∵
平面
,∴
,
再由条件可知:
,
,
∴
,
∴
平面
,∴
,∴
为
的垂心,
∴
,
∵
,
,
、
平面
,
∴
平面
,
∵
平面
,∴
.
33.【答案】
解:∵幂函数f(x)经过点(2,
),∴
=2(m2+m)-1
,
即
=2(m2+m)-1.∴m2+m=2.解得m=1或m=-2.又∵m∈N
,
∴m=1.∴f(x)=
,则函数的定义域为[0,+∞),并且在定义域上为增函数.由f(2-a)>f(a-1)得
,解得1≤a<
.∴a的取值范围为
.
34.【答案】
(1)解:由
及正弦定理得:
,
化简得
,
∴
,
又∵
,∴
.
(2)解:∵
的外接圆半径为2,
,
∴由正弦定理得
,解得
,
∴由余弦定理得
,
∴
,
∴
,当且仅当
时,等号成立,
∴
的周长的最大值为
.
35.【答案】
解:原不等式可化为
,
即
,
①当
即
时,
;
②当
时,即
时,原不等式的解集为
;
③当
即
时,
,
综上知:当
时,原不等式的解集为
;
当
时,原不等式的解集为
;
当
时,原不等式的解集为
.
36.【答案】
(1)解:根据题意得
,
,
平面
,
所以在
中,
,在
中,
,
所以在
中,
,
所以这辆汽车的速度为
.
(2)汽车从
往
行驶5秒时到达
处,此时
,
在
中,
,
所以在
中,由余弦定理得
,
即
,故
.
37.【答案】
(1)解:∵
,
∴
.
(2)解:由题意得
38.【答案】
(1)解:设
,则
,
则
又函数
为奇函数,
所以
,
所以
时,
所以
(2)解:根据(1)作出函数
的图象,如下图所示:
又函数
在区间
上单调递增,
结合函数
的图象,知
,
所以
,故实数
的取值范围是
39.【答案】
解:设边
的中点
,则由中点公式可得:
,即点
坐标为
所以边
上的中线先
的斜率
则由直线的斜截式方程可得:
这就是所求的边
上的中线所在的直线方程.
40.【答案】
(1)设事件A:从A地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均纯收入超过1万元,则
可以估计为
;
设事件B:从样本中B地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均纯收入超过1万元,则
可以估计为
.
由题意知,
的可能取值为0,1,2
?
所以
的分布列为:
X
0
1
2
所以
的数学期望为
.
(2)设事件C为“从样本中A地区的300户脱贫家庭中随机抽取4户,这4户家庭2020年人均年纯收入都超过1万元”,
假设样本中A地区2020年人均年纯收入超过1万元的户数相比2019年没有变化,则由2019年的样本数据可得
答案示例1:可以认为有变化,理由如下:
比较小,小概率事件一般不容易发生,一旦发生,就有理由认为样本中A地区2020
年人均年纯收入超过1万元的户数相比2019年发生了变化,所以可以认为有变化.
答案示例2:无法确定有没有变化,理由如下:
事件C是随机事件,
比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
一、单选题
1.已知函数
,若
在区间
上的最大值为
,则
的最小值是(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
2.下列函数图象与x轴都有公共点,其中不能用二分法求图中函数零点近似值的是(???
)
A.????????????????????????????????B.?
C.????????????????????????????D.?
3.已知函数
,若方程
有四个不同解
,且
,则
的取值范围为(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
4.在
中,内角
,
,
所对的边分别为
,
,
,且
,则
是(???
)
A.?钝角三角形???????????????????????B.?直角三角形???????????????????????C.?对角三角形???????????????????????D.?等边三角形
5.已知平面
平面
,
,
,则下列结论一定正确的是(???
)
A.?,
是平行直线??????B.?,
是异面直线??????C.?,
是共面直线??????D.?,
是不相交直线
6.已知函数
,则
=(
??)
A.?是奇函数,且在R上是增函数??????????????????????????????B.?是偶函数,且在R上是增函数
C.?是奇函数,且在R上是减函数??????????????????????????????D.?是偶函数,且在R上是减函数
7.在
中,A最大,C最小,且
,
,则此三角形的三边之比为(???
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
8.已知函数
的值域为
,则实数
的取值范围是(??
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
9.设
,若3是
与
的等比中项,则
的最小值为(??
).
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
10.已知集合
,
,若
,则
的取值范围是(?
??)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
11.(?
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
12.若
,以下选项能推出
的是(?
)
A.??????????????????B.??????????????????C.??????????????????D.?
13.设奇函数f(x)满足:①f(x)在(0,+∞)上单调递增;②f(1)=0,则不等式(x+1)f(x)>0的解集为(?
)
A.?(-∞,-1)∪(1,+∞)?????????B.?(0,1)?????????C.?(-∞,-1)?????????D.?(-∞,-1)∪(-1,0)∪(1,+∞)
14.对任意
,函数
在区间
上不是单调函数,则实数
的取值范围是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
15.在锐角三角形△ABC中,a,b,c分别是角A,B,C的对边,(a+b+c)(a+c﹣b)=
,则cosA+sinC的取值范围为(??
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
16.已知函数
是定义域为
的偶函数,且其图象关于直线
对称,若当
时,
,则
的零点的个数为(???
)
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
17.已知等差数列
的前
项和
有最大值,且
,则满足
的最大正整数
的值为(??
)
A.?6??????????????????????????????????????????B.?7??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
18.已知
,若函数
有三个零点,则实数
的取值范围是(
??)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
19.已知二次函数
交
轴于
两点(
不重合),交
轴于
点.
圆
过
三点.下列说法正确的是(?
)
①
圆心
在直线
上;②
的取值范围是
;③
圆
半径的最小值为
;④
存在定点
,使得圆
恒过点
.
A.?①②③??????????????????????????????????B.?①③④??????????????????????????????????C.?②③??????????????????????????????????D.?①④
20.设
,则关于
的不等式
的解集是(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
二、填空题
21.已知
,
,则
________.
22.设函数g(x)=ex+ae-x(x∈R)是奇函数,则实数a=________.
23.已知集合
,
,若
,则
________.
24.在R上定义运算?:x?y=x(1﹣y),若不等式(x﹣a)?(x+a)<1对任意的实数x成立,则a的取值范围是________.
25.函数y=2﹣x﹣
(x>0)的值域为________.
26.已知等比数列
的公比为q,关于x的不等式
有下列说法:
①当
吋,不等式的解集
②当
吋,不等式的解集为
③当
>0吋,存在公比q,使得不等式解集为
④存在公比q,使得不等式解集为R.
上述说法正确的序号是________.
27.如图,设圆M的半径为2,点C是圆M上的定点,A,B是圆M上的两个动点,则
的最小值是________.
28.已知函数
,则
________.
29.已知函数
(
)的图像经过点
,函数
的图像经过点
,则
________.
30.当
取到最大值时,
________.
三、解答题
31..已知A,B,C为锐角△ABC的内角,
=(sinA,sinBsinC),
=(1,﹣2),
⊥
.
(1).tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2).求tanAtanBtanC的最小值.
32.已知三棱柱
中,四边形
为矩形.
(1)记平面
与平面
的交线为,求证:
平面
;
(2)若
,求证:
.
33.已知幂函数f(x)=x(m2+m)-1(m∈N
),经过点(2,
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
34.在
中,角A
,
B
,
C所对的边分别为a
,
b
,
c
,
且
.
(1)求角A;
(2)若
的外接圆半径为2,求
周长的最大值.
35.解关于x的不等式
.
36.如图,一座山其高
为
,一辆汽车在一条水平的公路上沿直线从
往
匀速行驶,在
处测得山顶
的仰角为
,经过
后汽车到达
处,这时测得山顶
的仰角为
,且
.
(1)求这辆汽车的速度;
(2)若汽车从
往
行驶5秒时到达
处,求此时山顶
与汽车的距离
.
37..已知
(1).求
的值;
(2).求
的值.
38..已知
是定义在R上的奇函数,当
时,
.
(1).求函数
的表达式;
(2).若函数
在区间
上是单调的,试确定a的取值范围.
39..已知点
,求
的边
上的中线所在的直线方程。
40.在迎来中国共产党成立100周年的重要时刻,我国脱贫攻坚战取得全面胜利,创造了又一个彪炳史册的人间奇迹.习近平总书记指出:“脱贫摘帽不是终点,而是新生活?新奋斗的起点.”为了解脱贫家庭人均年纯收入情况,某扶贫工作组对
两个地区2019年脱贫家庭进行简单随机抽样,共抽取600户家庭作为样本,获得数据如下表:
A地区
B地区
2019年人均年纯收入超过1万元
120户
200户
2019年人均年纯收入未超过1万元
180户
100户
假设所有脱贫家庭的人均年纯收入是否超过1万元相互独立.
(1)分别从A地区和B地区2019年脱贫家庭中各随机抽取1户,记X为这2户家庭中2019年人均年纯收入超过1万元的户数,且把频率视作概率.求
的分布列和数学期望;
(2)从样本中A地区的300户脱贫家庭中随机抽取4户,发现这4户家庭2020年人均年纯收入都超过1万元.根据这个结果,能否认为样本中A地区2020年人均年纯收入超过1万元的户数相比2019年有变化?请说明理由.????
参考数据:
.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
A
3.【答案】
A
4.【答案】
A
5.【答案】
D
6.【答案】
A
7.【答案】
B
8.【答案】
D
9.【答案】
C
10.【答案】
A
11.【答案】
B
12.【答案】
C
13.【答案】
D
14.【答案】
A
15.【答案】
B
16.【答案】
C
17.【答案】
C
18.【答案】
A
19.【答案】
D
20.【答案】
D
二、填空题
21.【答案】
-28
22.【答案】
-1
23.【答案】
24.【答案】
25.【答案】(﹣∞,﹣2]
26.【答案】
③
27.【答案】
-2
28.【答案】
4
29.【答案】
,
.
30.【答案】
三、解答题
31.【答案】
(1)解:依题意有sinA=2sinBsinC.
在△ABC中,A=π﹣B﹣C,
所以sinA=sin(B+C)=sinBcosC+cosBsinC,
所以2sinBsinC=sinBcosC+cosBsinC.
因为△ABC为锐角三角形,所以cosB>0,cosC>0,
所以tanB+tanC=2tanBtanC,
所以tanB,tanBtanC,tanC成等差数列
(2)解:在锐角△ABC中,
tanA=tan(π﹣B﹣C)=﹣tan(B+C)=﹣
,
即tanAtanBtanC=tanA+tanB+tanC,
由(1)知tanB+tanC=2tanBtanC,
于是tanAtanBtanC=tanA+2tanBtanC≥
,
整理得tanAtanBtanC≥8,
当且仅当tanA=4时取等号,
故tanAtanBtanC的最小值为8
32.【答案】
(1)证明:由棱柱的性质得
,
∵
平面
,
平面
,∴
平面
,
∵
平面
,平面
与平面
的交线为,
∴
,
∵
平面
,
平面
,
∴
平面
.
(2)作
在
所在平面的投影于点
,延长
,
,
,交边长
、
、
于点
、
、
,
∵
,
,所以
,
∵
,
,
、
平面
,
∴
平面
,
∵
平面
,∴
,
再由条件可知:
,
,
∴
,
∴
平面
,∴
,∴
为
的垂心,
∴
,
∵
,
,
、
平面
,
∴
平面
,
∵
平面
,∴
.
33.【答案】
解:∵幂函数f(x)经过点(2,
),∴
=2(m2+m)-1
,
即
=2(m2+m)-1.∴m2+m=2.解得m=1或m=-2.又∵m∈N
,
∴m=1.∴f(x)=
,则函数的定义域为[0,+∞),并且在定义域上为增函数.由f(2-a)>f(a-1)得
,解得1≤a<
.∴a的取值范围为
.
34.【答案】
(1)解:由
及正弦定理得:
,
化简得
,
∴
,
又∵
,∴
.
(2)解:∵
的外接圆半径为2,
,
∴由正弦定理得
,解得
,
∴由余弦定理得
,
∴
,
∴
,当且仅当
时,等号成立,
∴
的周长的最大值为
.
35.【答案】
解:原不等式可化为
,
即
,
①当
即
时,
;
②当
时,即
时,原不等式的解集为
;
③当
即
时,
,
综上知:当
时,原不等式的解集为
;
当
时,原不等式的解集为
;
当
时,原不等式的解集为
.
36.【答案】
(1)解:根据题意得
,
,
平面
,
所以在
中,
,在
中,
,
所以在
中,
,
所以这辆汽车的速度为
.
(2)汽车从
往
行驶5秒时到达
处,此时
,
在
中,
,
所以在
中,由余弦定理得
,
即
,故
.
37.【答案】
(1)解:∵
,
∴
.
(2)解:由题意得
38.【答案】
(1)解:设
,则
,
则
又函数
为奇函数,
所以
,
所以
时,
所以
(2)解:根据(1)作出函数
的图象,如下图所示:
又函数
在区间
上单调递增,
结合函数
的图象,知
,
所以
,故实数
的取值范围是
39.【答案】
解:设边
的中点
,则由中点公式可得:
,即点
坐标为
所以边
上的中线先
的斜率
则由直线的斜截式方程可得:
这就是所求的边
上的中线所在的直线方程.
40.【答案】
(1)设事件A:从A地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均纯收入超过1万元,则
可以估计为
;
设事件B:从样本中B地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均纯收入超过1万元,则
可以估计为
.
由题意知,
的可能取值为0,1,2
?
所以
的分布列为:
X
0
1
2
所以
的数学期望为
.
(2)设事件C为“从样本中A地区的300户脱贫家庭中随机抽取4户,这4户家庭2020年人均年纯收入都超过1万元”,
假设样本中A地区2020年人均年纯收入超过1万元的户数相比2019年没有变化,则由2019年的样本数据可得
答案示例1:可以认为有变化,理由如下:
比较小,小概率事件一般不容易发生,一旦发生,就有理由认为样本中A地区2020
年人均年纯收入超过1万元的户数相比2019年发生了变化,所以可以认为有变化.
答案示例2:无法确定有没有变化,理由如下:
事件C是随机事件,
比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
同课章节目录
