人教版数学五年级上册6 不规则图形的面积课件(17张PPT)
文档属性
| 名称 | 人教版数学五年级上册6 不规则图形的面积课件(17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 20:45:59 | ||
图片预览






文档简介
(共17张PPT)
第5课时 不规则图形的面积
人教版-数学-五年级上册
多边形的面积
6
新课导入—探究新知—课堂检测—课堂小结—课后作业
教学目标
1.通过与同伴交流估算面积的方法,培养合作意识,借助操作等实践活动自主解决问题。
2.在估计不规则图形面积的过程中,培养空间观念以及估算意识和能力。
3.学习用数方格的方法计算不规则图形的面积,能估计不规则图形的面积大小,并能用不同方法灵活估算面积。
教学重难点:
1.掌握用方格纸和参照规则图形面积估计不规则图形面积的方法。
2.能用不同方法灵活估算不规则图形的面积。
我们已经会计算组合图形的面积了,那么生活中遇到不规则图形我们如何来估算它的面积呢?
新 课 导 入
图中每个小方格的面积是 1 cm2 ,请你估计这片叶子的面积。
探 究 新 知
阅读与理解
这片叶子的形状不规则,怎么计算面积呢?
知道小方格的面积,求叶子的面积。
探 究 新 知
分析与解答
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2~36cm2之间。
探 究 新 知
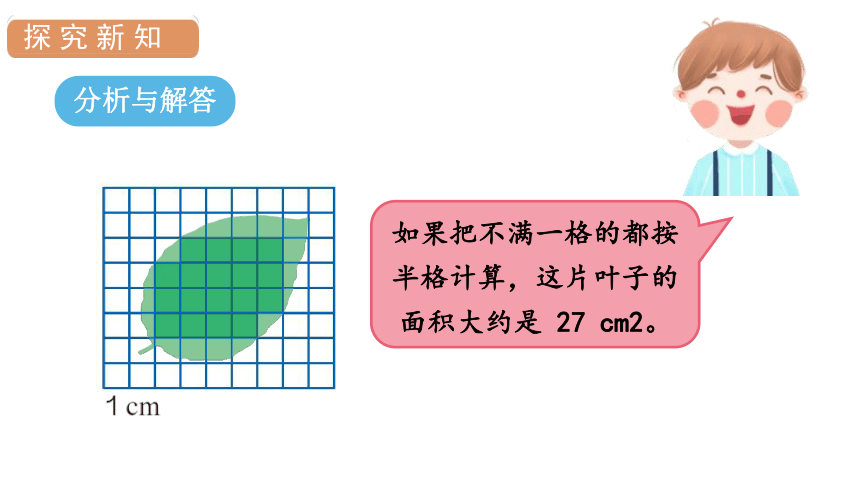
如果把不满一格的都按半格计算,这片叶子的面积大约是 27 cm2。
分析与解答
探 究 新 知
分析与解答
谁还有不同的方法?
将叶子的图形近似转化成平行四边形
S = ah
= 5×6
= 30(cm2 )
因此,叶子的面积大约是 30 cm2。
探 究 新 知
分析与解答
将叶子的图形近似转化成长方形
S = ab
= 5×6
= 30(cm2 )
因此,叶子的面积大约是 30 cm2。
探 究 新 知
谁还有不同的方法?
通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?
先通过数方格确定图形面积的范围,再估算图形的面积。
不规则的图形可以转化为学过的图形进行估算。
回顾与反思
探 究 新 知
1.图中每个小方格的面积为 1 cm2,计算阴影部分的面积。
三角形 + 梯形
5×4÷2 +(5+2)×4÷2
= 24(cm2)
课 堂 检 测
近似转化成长方形
8×4 = 32(cm2)
阴影部分面积大约是 32 cm2。
1.图中每个小方格的面积为 1 cm2,计算阴影部分的面积。
课 堂 检 测
2.图中每个小方格的面积为 1 m2,请你估计这个池塘的面积。
S =ab
=12×9
=108(m2 )
答:这个池塘的面积大约是 108 m2。
课 堂 检 测
通过本节课的学习,你有什么收获?
课 堂 小 结
1.请你采集几片树叶,利用方格纸估计叶子的面积。
你能像这样估一估手掌的面积吗?
课 后 作 业
2.学校校园里有一块长方形的地,想种上红花、黄花和绿草。一种设计方案如下图。你能分别算出红花、黄花、绿草的种植面积吗?
18m
绿草:
(18÷2)×(12÷2)÷2×4=108(m2)
黄花和红花面积相等:
(18×12-108)÷2=54(m2)
答:红花、黄花、绿草的种植面积分别是 54 m2 、54 m2 、108 m2。
课 后 作 业
谢谢
第5课时 不规则图形的面积
人教版-数学-五年级上册
多边形的面积
6
新课导入—探究新知—课堂检测—课堂小结—课后作业
教学目标
1.通过与同伴交流估算面积的方法,培养合作意识,借助操作等实践活动自主解决问题。
2.在估计不规则图形面积的过程中,培养空间观念以及估算意识和能力。
3.学习用数方格的方法计算不规则图形的面积,能估计不规则图形的面积大小,并能用不同方法灵活估算面积。
教学重难点:
1.掌握用方格纸和参照规则图形面积估计不规则图形面积的方法。
2.能用不同方法灵活估算不规则图形的面积。
我们已经会计算组合图形的面积了,那么生活中遇到不规则图形我们如何来估算它的面积呢?
新 课 导 入
图中每个小方格的面积是 1 cm2 ,请你估计这片叶子的面积。
探 究 新 知
阅读与理解
这片叶子的形状不规则,怎么计算面积呢?
知道小方格的面积,求叶子的面积。
探 究 新 知
分析与解答
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2~36cm2之间。
探 究 新 知
如果把不满一格的都按半格计算,这片叶子的面积大约是 27 cm2。
分析与解答
探 究 新 知
分析与解答
谁还有不同的方法?
将叶子的图形近似转化成平行四边形
S = ah
= 5×6
= 30(cm2 )
因此,叶子的面积大约是 30 cm2。
探 究 新 知
分析与解答
将叶子的图形近似转化成长方形
S = ab
= 5×6
= 30(cm2 )
因此,叶子的面积大约是 30 cm2。
探 究 新 知
谁还有不同的方法?
通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?
先通过数方格确定图形面积的范围,再估算图形的面积。
不规则的图形可以转化为学过的图形进行估算。
回顾与反思
探 究 新 知
1.图中每个小方格的面积为 1 cm2,计算阴影部分的面积。
三角形 + 梯形
5×4÷2 +(5+2)×4÷2
= 24(cm2)
课 堂 检 测
近似转化成长方形
8×4 = 32(cm2)
阴影部分面积大约是 32 cm2。
1.图中每个小方格的面积为 1 cm2,计算阴影部分的面积。
课 堂 检 测
2.图中每个小方格的面积为 1 m2,请你估计这个池塘的面积。
S =ab
=12×9
=108(m2 )
答:这个池塘的面积大约是 108 m2。
课 堂 检 测
通过本节课的学习,你有什么收获?
课 堂 小 结
1.请你采集几片树叶,利用方格纸估计叶子的面积。
你能像这样估一估手掌的面积吗?
课 后 作 业
2.学校校园里有一块长方形的地,想种上红花、黄花和绿草。一种设计方案如下图。你能分别算出红花、黄花、绿草的种植面积吗?
18m
绿草:
(18÷2)×(12÷2)÷2×4=108(m2)
黄花和红花面积相等:
(18×12-108)÷2=54(m2)
答:红花、黄花、绿草的种植面积分别是 54 m2 、54 m2 、108 m2。
课 后 作 业
谢谢
