第02讲 矩形的性质与判定(考点讲解)(含答案)
文档属性
| 名称 | 第02讲 矩形的性质与判定(考点讲解)(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 22:42:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第02讲
矩形的性质与判定
【教学要求】
1.能运用综合法证明矩形判定定理。
2.体会证明过程中所运用的归纳概括以及转化等数学思想方法。
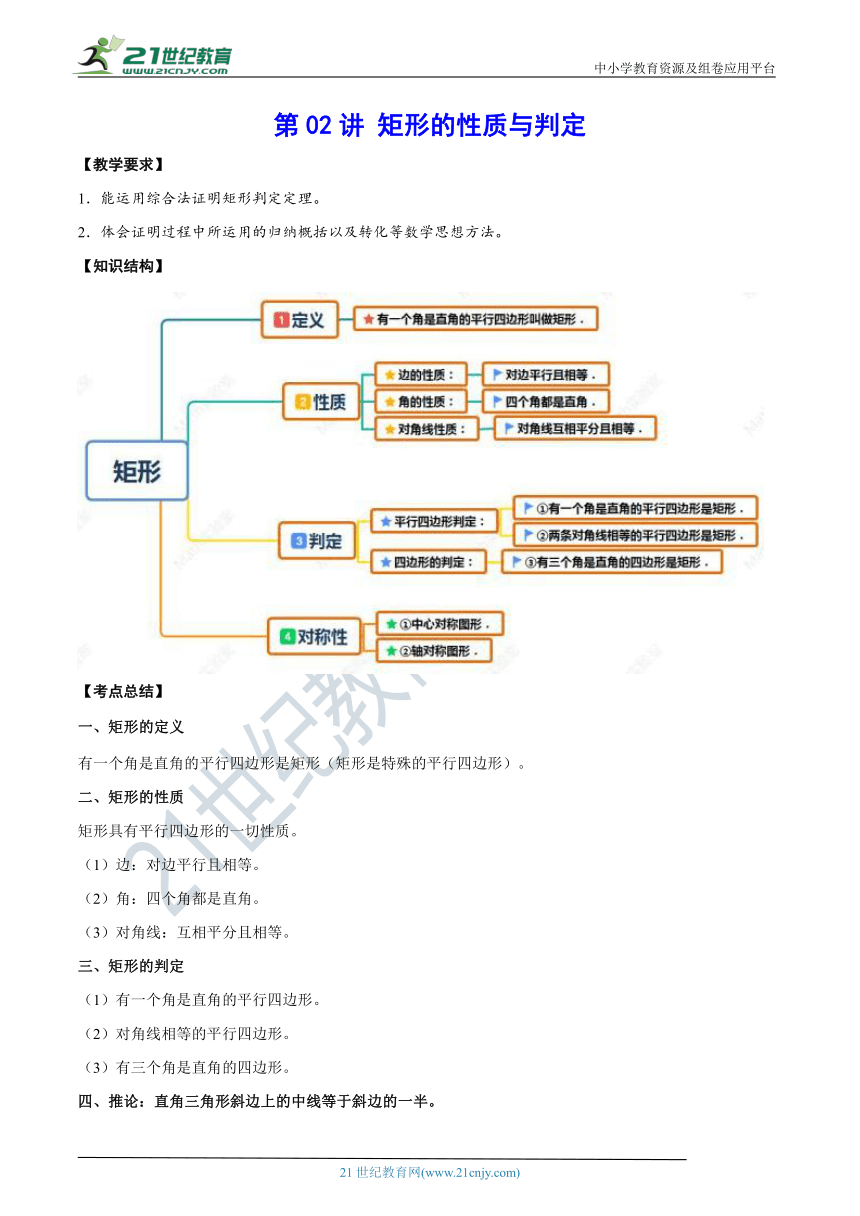
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、矩形的定义
有一个角是直角的平行四边形是矩形(矩形是特殊的平行四边形)。
二、矩形的性质
矩形具有平行四边形的一切性质。
(1)边:对边平行且相等。
(2)角:四个角都是直角。
(3)对角线:互相平分且相等。
三、矩形的判定
(1)有一个角是直角的平行四边形。
(2)对角线相等的平行四边形。
(3)有三个角是直角的四边形。
四、推论:直角三角形斜边上的中线等于斜边的一半。
【例题讲解】
【类型】一、矩形的性质
例1、
如图,矩形ABCD的周长为18cm,M是CD的中点,且AM⊥BM,则矩形ABCD的两邻边长分别是(
)21cnjy.com
(?http:?/??/?www.21cnjy.com?/??)
A.3cm和6cm
B.6cm和12cm
C.4cm和5cm
D.以上都不对
【解析】A
首先证得△ADM≌△BCM,可得出∠AMD=∠BMC,由此可求出两角的度数,即可得出DM、MC的长,由此得解.【来源:21·世纪·教育·网】
∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC,
又∵M是CD的中点
∴MD=MC,
∴△ADM≌△BCM,
∴∠AMD=∠BMC
∵AM⊥BM,
∴∠AMD=∠BMC=45°,
∴AD=DM,BC=CM,
∵矩形ABCD的周长为18cm,
∴AD=3cm,DC=6cm,
故选A.
【总结与反思】此题运用了矩形的定义与性质:四个角都是90°.
【训练】如图,Rt△ABC中,∠C=90°,
(?http:?/??/?www.21cnjy.com?)AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是 _________ .
21·世纪
教育网
(?http:?/??/?www.21cnjy.com?/??)
【答案】;
提示:因为ECFP为矩形,所以有EF=PC.PC最小时是直角三角形斜边上的高.
【类型】二、矩形的判定
例2、如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于
F,点O既是AC的中点,又是EF的中点.
(?http:?/??/?www.21cnjy.com?/??)
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
【解析】解:(1)证明:∵BE⊥AC.DF⊥AC,∴∠BEO=∠DFO=90°.
∵点O是EF的中点,∴OE=OF.
又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).
(2)四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,∴OB=OD.
又∵OA=OC,∴四边形ABCD是平行四边形.
∵OA=BD,OA=AC,∴BD=AC.∴平行四边形ABCD是矩形.
(1)根据垂直可得∠BEO=∠DFO=90°,再由点O是EF的中点可得OE=OF,再加上对顶角
∠DOF=∠BOE,可利用ASA证明△BOE≌△DOF.
(2)根据△BOE≌△DOF可得D
(?http:?/??/?www.21cnjy.com?)O=BO,再加上条件AO=CO可得四边形ABCD是平行四边形,再证明DB=AC,可根据对角线相等的平行四边形是矩形证出结论.www-2-1-cnjy-com
【总结与反思】根据矩形的性质即可解出此题.
【训练】
如图,将□ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
(?http:?/??/?www.21cnjy.com?/??)
证明:(1)在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,
∴BE=DC,
∴四边形BECD为平行四边形,
∴BD=EC.
∴在△ABD与△BEC中,
,
∴△ABD≌△BEC(SSS);
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴OC+OB=OD+OE,即BC=ED,
∴平行四边形BECD为矩形.
【类型】三、直角三角形斜边上的中线的性质
例3、如图,∠MON=90°,矩形ABCD
(?http:?/??/?www.21cnjy.com?)的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为【
】21教育网
(?http:?/??/?www.21cnjy.com?/??)
A. B. C. D.
【解析】A
如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=2,BC=1,∴OE=AE=AB=1.
DE=,
∴OD的最大值为:.故选A.
(?http:?/??/?www.21cnjy.com?/??)
【总结与反思】
此题是对直角三角形斜边上的中线的性质的灵活运用.
【训练】如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )www.21-cn-jy.com
A.20
B.12
C.14
D.13
(?http:?/??/?www.21cnjy.com?/??)
【答案】C;
解:∵AB=AC,AD平分∠BAC,BC=8,
∴AD⊥BC,CD=BD=BC=4,
∵点E为AC的中点,
∴DE=CE=AC=5,
∴△CDE的周长=CD+DE+CE=4+5+5=14.2-1-c-n-j-y
【总结升华】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.21
cnjy
com
【训练】如图所示,已知平行
(?http:?/??/?www.21cnjy.com?)四边形ABCD,AC、BD相交于点O,P是平行四边形ABCD外一点,且∠APC=∠BPD=90°.求证:平行四边形ABCD是矩形.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?/??)
解:连接OP.
∵
四边形ABCD是平行四边形.
(?http:?/??/?www.21cnjy.com?/??)
∴
AO=CO,BO=DO,
∵
∠APC=∠BPD=90°,
∴
OP=AC,OP=BD,
∴
AC=BD.
∴
四边形ABCD是矩形.
【类型】四、矩形中的折叠问题
例4、如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )2·1·c·n·j·y
A、4 B、3 C、4.5 D、5
【解析】A
由折叠可得,BC’=
3,BF+FC’=
9,
根据勾股定理可得:在△C’BF中,
BF=4
故选A.
【总结与反思】根据折叠的性质和勾股定理即可解出此题.
【类型】五、与矩形对角线相关的拓展问题
例5、如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD
于F,则PE+FF的值是(
)21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?/??)
A、
B、2
C、
D、
A
【解析】B
连接OP,过D作DM⊥AC于M,求出AC长,根据三角形的面积公式求出CM的值,根据代入求出PE+PF=DM即可.21·cn·jy·com
连接OP,过D作DM⊥AC于M,
∵四边形ABCD是矩形,
∴AO=OC=AC,OD=OB=BD,AC=BD,∠ADC=90°
∴OA=OD,
由勾股定理得:
,
,
(?http:?/??/?www.21cnjy.com?/??)
,
即,
故选B.
【总结与反思】根据矩形对角线相等且互相平分即可解出此题.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第02讲
矩形的性质与判定
【教学要求】
1.能运用综合法证明矩形判定定理。
2.体会证明过程中所运用的归纳概括以及转化等数学思想方法。
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、矩形的定义
有一个角是直角的平行四边形是矩形(矩形是特殊的平行四边形)。
二、矩形的性质
矩形具有平行四边形的一切性质。
(1)边:对边平行且相等。
(2)角:四个角都是直角。
(3)对角线:互相平分且相等。
三、矩形的判定
(1)有一个角是直角的平行四边形。
(2)对角线相等的平行四边形。
(3)有三个角是直角的四边形。
四、推论:直角三角形斜边上的中线等于斜边的一半。
【例题讲解】
【类型】一、矩形的性质
例1、
如图,矩形ABCD的周长为18cm,M是CD的中点,且AM⊥BM,则矩形ABCD的两邻边长分别是(
)21cnjy.com
(?http:?/??/?www.21cnjy.com?/??)
A.3cm和6cm
B.6cm和12cm
C.4cm和5cm
D.以上都不对
【解析】A
首先证得△ADM≌△BCM,可得出∠AMD=∠BMC,由此可求出两角的度数,即可得出DM、MC的长,由此得解.【来源:21·世纪·教育·网】
∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC,
又∵M是CD的中点
∴MD=MC,
∴△ADM≌△BCM,
∴∠AMD=∠BMC
∵AM⊥BM,
∴∠AMD=∠BMC=45°,
∴AD=DM,BC=CM,
∵矩形ABCD的周长为18cm,
∴AD=3cm,DC=6cm,
故选A.
【总结与反思】此题运用了矩形的定义与性质:四个角都是90°.
【训练】如图,Rt△ABC中,∠C=90°,
(?http:?/??/?www.21cnjy.com?)AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是 _________ .
21·世纪
教育网
(?http:?/??/?www.21cnjy.com?/??)
【答案】;
提示:因为ECFP为矩形,所以有EF=PC.PC最小时是直角三角形斜边上的高.
【类型】二、矩形的判定
例2、如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于
F,点O既是AC的中点,又是EF的中点.
(?http:?/??/?www.21cnjy.com?/??)
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
【解析】解:(1)证明:∵BE⊥AC.DF⊥AC,∴∠BEO=∠DFO=90°.
∵点O是EF的中点,∴OE=OF.
又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).
(2)四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,∴OB=OD.
又∵OA=OC,∴四边形ABCD是平行四边形.
∵OA=BD,OA=AC,∴BD=AC.∴平行四边形ABCD是矩形.
(1)根据垂直可得∠BEO=∠DFO=90°,再由点O是EF的中点可得OE=OF,再加上对顶角
∠DOF=∠BOE,可利用ASA证明△BOE≌△DOF.
(2)根据△BOE≌△DOF可得D
(?http:?/??/?www.21cnjy.com?)O=BO,再加上条件AO=CO可得四边形ABCD是平行四边形,再证明DB=AC,可根据对角线相等的平行四边形是矩形证出结论.www-2-1-cnjy-com
【总结与反思】根据矩形的性质即可解出此题.
【训练】
如图,将□ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
(?http:?/??/?www.21cnjy.com?/??)
证明:(1)在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,
∴BE=DC,
∴四边形BECD为平行四边形,
∴BD=EC.
∴在△ABD与△BEC中,
,
∴△ABD≌△BEC(SSS);
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴OC+OB=OD+OE,即BC=ED,
∴平行四边形BECD为矩形.
【类型】三、直角三角形斜边上的中线的性质
例3、如图,∠MON=90°,矩形ABCD
(?http:?/??/?www.21cnjy.com?)的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为【
】21教育网
(?http:?/??/?www.21cnjy.com?/??)
A. B. C. D.
【解析】A
如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=2,BC=1,∴OE=AE=AB=1.
DE=,
∴OD的最大值为:.故选A.
(?http:?/??/?www.21cnjy.com?/??)
【总结与反思】
此题是对直角三角形斜边上的中线的性质的灵活运用.
【训练】如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )www.21-cn-jy.com
A.20
B.12
C.14
D.13
(?http:?/??/?www.21cnjy.com?/??)
【答案】C;
解:∵AB=AC,AD平分∠BAC,BC=8,
∴AD⊥BC,CD=BD=BC=4,
∵点E为AC的中点,
∴DE=CE=AC=5,
∴△CDE的周长=CD+DE+CE=4+5+5=14.2-1-c-n-j-y
【总结升华】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.21
cnjy
com
【训练】如图所示,已知平行
(?http:?/??/?www.21cnjy.com?)四边形ABCD,AC、BD相交于点O,P是平行四边形ABCD外一点,且∠APC=∠BPD=90°.求证:平行四边形ABCD是矩形.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?/??)
解:连接OP.
∵
四边形ABCD是平行四边形.
(?http:?/??/?www.21cnjy.com?/??)
∴
AO=CO,BO=DO,
∵
∠APC=∠BPD=90°,
∴
OP=AC,OP=BD,
∴
AC=BD.
∴
四边形ABCD是矩形.
【类型】四、矩形中的折叠问题
例4、如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )2·1·c·n·j·y
A、4 B、3 C、4.5 D、5
【解析】A
由折叠可得,BC’=
3,BF+FC’=
9,
根据勾股定理可得:在△C’BF中,
BF=4
故选A.
【总结与反思】根据折叠的性质和勾股定理即可解出此题.
【类型】五、与矩形对角线相关的拓展问题
例5、如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD
于F,则PE+FF的值是(
)21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?/??)
A、
B、2
C、
D、
A
【解析】B
连接OP,过D作DM⊥AC于M,求出AC长,根据三角形的面积公式求出CM的值,根据代入求出PE+PF=DM即可.21·cn·jy·com
连接OP,过D作DM⊥AC于M,
∵四边形ABCD是矩形,
∴AO=OC=AC,OD=OB=BD,AC=BD,∠ADC=90°
∴OA=OD,
由勾股定理得:
,
,
(?http:?/??/?www.21cnjy.com?/??)
,
即,
故选B.
【总结与反思】根据矩形对角线相等且互相平分即可解出此题.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
