2.3匀变速直线运动的位移与时间的关系 同步练习(Word版含答案)
文档属性
| 名称 | 2.3匀变速直线运动的位移与时间的关系 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 171.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览



文档简介
吉林省白城市通榆县第一中学2021—2022学年上学期高一物理必修第一册第二章匀变速直线运动的研究
第三节匀变速直线运动的位移与时间的关系
一、选择题(本大题共12小题,7-12为多选题,每小题4分,选不全2分,共48分)
一辆汽车以的速度在平直的公路上行驶,看到前面有一障碍物时以加速度紧急刹车,则小车在开始刹车后6s内的位移是????
A.
40m
B.
30m
C.
120m
D.
60m
一物体在某点从静止开始做匀加速直线运动,其中物体运动的位移为x、加速度为a、速度为v、运动时间为t,则下列图像一定错误的是
A.
B.
C.
D.
在交警处理某次交通事故时,通过监控仪器扫描,输入计算机后得到该汽车在水平路面上刹车过程中的位移随时间变化的规律为:的单位是m,t的单位是则该汽车在路面上留下的刹车痕迹长度为
A.
25m
B.
50m
C.
100m
D.
200m
2018年10月23日港珠澳大桥正式通车,它是目前世界上最长的跨海大桥,为香港、澳门、珠海三地提供了一条快捷通道。图甲是港珠澳大桥中的一段,一辆小汽车在长度为的平直桥面上提速,图乙是该车在该段的车速的平方与位移的关系。则关于小汽车通过该段平直桥面的加速度和时间分别为?
?
?
A.
,6s
B.
,3s
C.
,5s
D.
,
跳伞运动员从高空悬停的直升机上跳下,运动员沿竖直方向运动的图像如图所示,下列说法正确的是?
?
?
A.
运动员在内的平均速度小于
B.
末开始运动员处于静止状态
C.
末运动员的速度方向改变
D.
内运动员做加速度逐渐减小的减速运动
一物体做匀变速直线运动,下列说法中正确的是
A.
物体的末速度一定与时间成正比
B.
物体的位移一定与时间的二次方成正比
C.
物体的速度在一定时间内的变化量与这段时间成正比
D.
若为匀加速直线运动,速度和位移都随时间增加;若为匀减速直线运动,速度和位移都随时间减小
物体做初速度为零的匀加速直线,前2s内的位移是8m,则?
?
A.
物体的加速度是
B.
物体的加速度是
C.
物体前4s内的位移是32m
D.
物体2s末的速度是
小李讲了一个龟兔赛跑的故事,按照小李讲的故事情节,兔子和乌龟的位移时间图象如图所示,由图可知
A.
兔子和乌龟是同时同地出发
B.
兔子和乌龟在比赛途中相遇过两次
C.
乌龟做的是匀速直线运动,兔子是沿着折线跑的
D.
乌龟先通过预定位移到达终点
在一次救灾活动中,一辆救灾汽车由静止开始做匀变速直线运动,刚运动了,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经停在巨石前.则关于汽车的运动情况,下列说法正确的是
A.
加速、减速中的加速度大小之比为等于
B.
加速、减速中的平均速度大小之比等于
C.
加速、减速中的位移大小之比等于
D.
加速、减速中的加速度大小之比等于
甲、乙两汽车在同一条平直公路上同向运动,其速度时间图象分别如图中甲、乙两条图线所示.下列对甲、乙运动描述中正确的是
A.
时间内乙的加速度逐渐减小
B.
时间内甲的加速度逐渐增大
C.
时间内的某时刻甲、乙加速度相等
D.
T时刻两者相遇
某质点的位移随时间变化规律的关系是,s与t的单位分别为m和s,下列说法正确的是
A.
?,?
B.
?,?
C.
2?s内的位移为24?m
D.
2?s末的速度为24?
关于匀变速直线运动的说法,正确的是
A.
某段时间内的平均速度等于这段时间内的初速度与末速度之和的一半
B.
在任意相等的时间内位移的变化量相等
C.
在任意相等的时间内速度的变化量相等
D.
某段时间内的平均速度,等于位移中点的瞬时速度
二、实验题(本大题共2小题,每小题各6分,共12分)
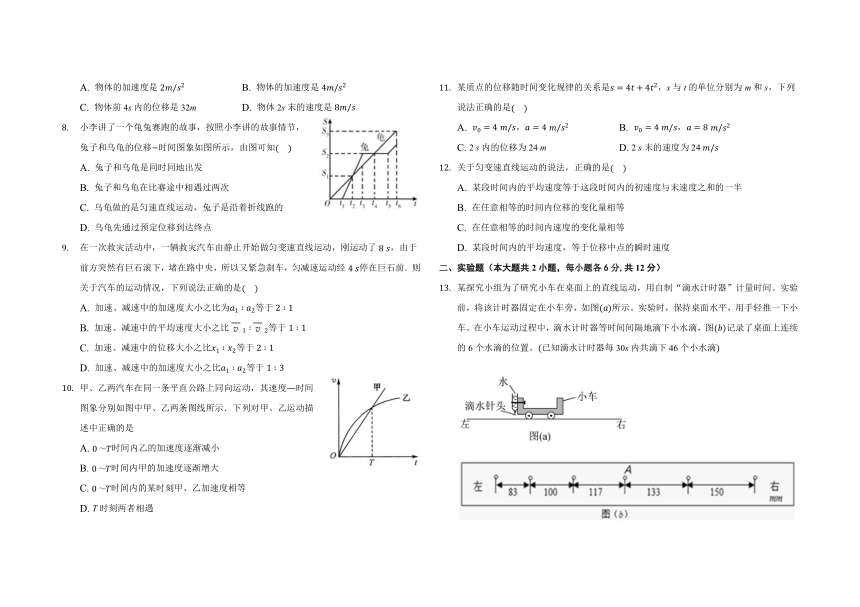
某探究小组为了研究小车在桌面上的直线运动,用自制“滴水计时器”计量时间。实验前,将该计时器固定在小车旁,如图所示。实验时,保持桌面水平,用手轻推一下小车。在小车运动过程中,滴水计时器等时间间隔地滴下小水滴,图记录了桌面上连续的6个水滴的位置。已知滴水计时器每30s内共滴下46个小水滴
由图可知,小车在桌面上是_________填“从右向左”或“从左向右”运动的。
该小组同学根据图的数据判断出小车做匀变速运动。小车运动到图中A点位置时的速度大小为_______,加速度大小为_______。结果均保留2位有效数字
如图所示为实验中小车在重物牵引下得到的一条纸带,相邻计数点间有四个点未标出,打点计时器所接电源的频率为50Hz,则打B点时小车的速度大小为______,小车的加速度大小为______。保留三位有效数字
三、计算题(本大题共4小题,写出必理论根据和主要方程式,每小题各10分,共40分)
一辆汽车在平直的公路上以的速度行驶,刹车后开始做匀减速运动,加速度大小为从刹车开始计时,试求:
汽车还能运动的时间t;
汽车能通过的最大距离x;
汽车在前4秒内平均速度.
某一长直的赛道上,有一辆F1赛车前方200m有一安全车正以的速度匀速前进,此时赛车从静止出发以的加速度追赶.试求:
赛车追上安全车之前两车相距的最远距离多少?
赛车经过多长时间追上安全车?
赛车追上安全车时的速度为多少?
一辆汽车以的加速度由静止开始加速直线行驶。
时该汽车的速度大小是多少
如果此汽车以同样的加速度从的速度开始匀减速行驶,问
末汽车的速度大小是多少?
内此汽车的位移大小是多少
一个质点做匀加速直线运动,在相邻的两个1s内通过的位移分别为和。试求:
该质点的加速度大小a;
该质点在这两个1s末的瞬时速度和的大小。
参考答案
1.
A
解析取初速度方向为正方向,则,,根据速度时间关系可知,汽车做匀减速运动的时间为:,故刹车后6s内的位移实为刹车后匀减速运动4s内的位移,此时速度已经减速到零,所以位移为:,故A正确,故BCD错误。故选A。??
2.
D解析从静止开始的匀加速直线运动,则加速度a恒定不变,D图错误;,A图正确;,B图正确;,故C图正确。
本题选错误选项,故选D??
3.
B
解析根据可知,初速度,加速度。
刹车后做匀减速运动的位移为刹车痕迹长度:,故ADC错误,B正确。故选B。??
4.
B
解析由匀变速运动规律,结合图象可知,,加速度,得,由,知,故B正确,ACD错误。
故选B。??
5.
D
解析A.内,若运动员做匀加速运动,平均速度为,根据图像的“面积”等于位移可知,运动员的位移大于匀加速运动的位移,所以由公式,得知:内的平均速度大于匀加速运动的平均速度,故A错误;
B.由图知,15s末开始运动员做匀速直线运动,故B错误;
C.由图速度正负看出,运动员的速度一直沿正向,速度方向没有改变,故C错误;
D.图像的斜率减小,则其加速度减小,故运动员做加速度减小的减速运动,故D正确。故选D。??
6.C
解析根据和可知,速度只有在初速度为零的情况下,与时间成正比,位移只有在初速度为零时,与时间的平方成正比,故AB错误;
C.由可知,a一定,则物体的速度在一定时间内发生的变化与这段时间成正比,故C正确;
D.当物体做匀减速运动时,速度减小但位移可以增大,故D错误。故选:C。??
7.
BCD
解析AB、根据得,,故A错误,B正确;
C、物体在前4s内的位移,故C正确;
D、物体2s末的速度是?,故D正确。故选:BCD。??
8.
BD
解析A.由图读出,兔子和乌龟是从同地不同时刻出发的,兔子在乌龟出发后时间出发,故A错误;
B.在和两个时刻,兔子和乌龟位移相同,两者相遇,说明兔子和乌龟在比赛途中相遇过两次,故B正确;
C.乌龟做的是匀速直线运动,兔子先做匀速直线运动,在时间内静止不动,时刻以后又沿原方向做匀速直线运动,兔子不是沿着折线跑的,故C错误;
D.由图看出,时刻乌龟到达终点,而兔子还没有到达终点,说明乌龟先通过预定位移到达终点,故D正确。
故选BD。
9.
BC
解析设加速阶段的末速度为v,则加速阶段的加速度大小为,减速阶段的加速度大小,则加速度大小之比为1:2,故AD错误;
B.根据匀变速直线运动的平均速度公式得,加速阶段和减速阶段的平均速度之比为1:1,故B正确;
C.根据,知加速阶段和减速阶段的位移之比为2:1,故C正确。
故选BC。
10.AC
解析根据加速度图象中图线切线的斜率表示加速度大小,则有甲做匀加速运动,乙的加速度逐渐减小,在阶段,对乙图作切线,能找到一条与甲图线平行,即某时刻甲、乙加速度相等?,选项B错误,选项A、C正确;
D.因不知道两车初位置,故T时刻两者速度相等,不一定相遇,选项D错误。
故选AC。??
11.
BC
解:A、B、质点做直线运动的位移x与时间t的关系为;根据匀变速直线运动的位移时间关系公式,可得初速度,加速度;故A错误,B正确;
C、时的位置坐标为零;2s内的位移为:;故C正确;
D、2s末的速度为:;故D错误;
故选:BC。
12.AC
解析:A、匀变速直线运动某段时间内的平均速度等于这段时间内的初速度与末速度和的一半,故A正确.
B、由可知,只有连续相等的时间内位移的变化相等,可知B不正确.
C、由,a是常数,可知在任意相等的时间内速度的变化相等,故C正确;
D、某段时间内的平均速度,等于时间中点的瞬时速度;故D错误;
故选:AC
13.答案:从右向左;,。
解析
:由于用手轻推一下小车,则小车做减速运动,根据桌面上连续6个水滴的位置,可知,小车从右向左做减速运动;
已知滴水计时器每30s内共滴下46个小水滴,
那么各点时间间隔为:
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,有:
,
根据匀变速直线运动的推论公式可以求出加速度,得:
?,
那么加速度的大小为。
故答案为:从右向左;,。??
14.答案:?
解析:相邻计数点间有四个点未标出,打点计时器所接电源的频率为50Hz,相邻计数点间的时间间隔为,根据推论匀变速直线运动中,某段时间内的平均速度等于中间时刻的瞬时速度可知B点时小车的速度;
由逐差法公式可得
故答案为:;。
15.解:汽车还能运动的时间:
汽车能通过的最大距离:
汽车在前4秒内的位移:
平均速度:。
16.解:当两车速度相等时相距最远,由速度关系得:
解得:
即经过5s两车相距最远。当两车相距最远时,赛车位移:
安全车位移:
两车之间距离赛
解得:
设赛车经过时间t追上安全车,则有:
解得:
赛车追上安全车的速度是
赛车追上安全车时的速度为
17.解:时该汽车的速度
汽车停下用时
末汽车的速度
内汽车已停下,位移
18.解:由匀变速直线运动的推论:可知,加速度:;
质点的速度:,
速度:;
答:该质点的加速度大小a为;
该质点在这两个1s末的瞬时速度和的大小分别为:、
第三节匀变速直线运动的位移与时间的关系
一、选择题(本大题共12小题,7-12为多选题,每小题4分,选不全2分,共48分)
一辆汽车以的速度在平直的公路上行驶,看到前面有一障碍物时以加速度紧急刹车,则小车在开始刹车后6s内的位移是????
A.
40m
B.
30m
C.
120m
D.
60m
一物体在某点从静止开始做匀加速直线运动,其中物体运动的位移为x、加速度为a、速度为v、运动时间为t,则下列图像一定错误的是
A.
B.
C.
D.
在交警处理某次交通事故时,通过监控仪器扫描,输入计算机后得到该汽车在水平路面上刹车过程中的位移随时间变化的规律为:的单位是m,t的单位是则该汽车在路面上留下的刹车痕迹长度为
A.
25m
B.
50m
C.
100m
D.
200m
2018年10月23日港珠澳大桥正式通车,它是目前世界上最长的跨海大桥,为香港、澳门、珠海三地提供了一条快捷通道。图甲是港珠澳大桥中的一段,一辆小汽车在长度为的平直桥面上提速,图乙是该车在该段的车速的平方与位移的关系。则关于小汽车通过该段平直桥面的加速度和时间分别为?
?
?
A.
,6s
B.
,3s
C.
,5s
D.
,
跳伞运动员从高空悬停的直升机上跳下,运动员沿竖直方向运动的图像如图所示,下列说法正确的是?
?
?
A.
运动员在内的平均速度小于
B.
末开始运动员处于静止状态
C.
末运动员的速度方向改变
D.
内运动员做加速度逐渐减小的减速运动
一物体做匀变速直线运动,下列说法中正确的是
A.
物体的末速度一定与时间成正比
B.
物体的位移一定与时间的二次方成正比
C.
物体的速度在一定时间内的变化量与这段时间成正比
D.
若为匀加速直线运动,速度和位移都随时间增加;若为匀减速直线运动,速度和位移都随时间减小
物体做初速度为零的匀加速直线,前2s内的位移是8m,则?
?
A.
物体的加速度是
B.
物体的加速度是
C.
物体前4s内的位移是32m
D.
物体2s末的速度是
小李讲了一个龟兔赛跑的故事,按照小李讲的故事情节,兔子和乌龟的位移时间图象如图所示,由图可知
A.
兔子和乌龟是同时同地出发
B.
兔子和乌龟在比赛途中相遇过两次
C.
乌龟做的是匀速直线运动,兔子是沿着折线跑的
D.
乌龟先通过预定位移到达终点
在一次救灾活动中,一辆救灾汽车由静止开始做匀变速直线运动,刚运动了,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经停在巨石前.则关于汽车的运动情况,下列说法正确的是
A.
加速、减速中的加速度大小之比为等于
B.
加速、减速中的平均速度大小之比等于
C.
加速、减速中的位移大小之比等于
D.
加速、减速中的加速度大小之比等于
甲、乙两汽车在同一条平直公路上同向运动,其速度时间图象分别如图中甲、乙两条图线所示.下列对甲、乙运动描述中正确的是
A.
时间内乙的加速度逐渐减小
B.
时间内甲的加速度逐渐增大
C.
时间内的某时刻甲、乙加速度相等
D.
T时刻两者相遇
某质点的位移随时间变化规律的关系是,s与t的单位分别为m和s,下列说法正确的是
A.
?,?
B.
?,?
C.
2?s内的位移为24?m
D.
2?s末的速度为24?
关于匀变速直线运动的说法,正确的是
A.
某段时间内的平均速度等于这段时间内的初速度与末速度之和的一半
B.
在任意相等的时间内位移的变化量相等
C.
在任意相等的时间内速度的变化量相等
D.
某段时间内的平均速度,等于位移中点的瞬时速度
二、实验题(本大题共2小题,每小题各6分,共12分)
某探究小组为了研究小车在桌面上的直线运动,用自制“滴水计时器”计量时间。实验前,将该计时器固定在小车旁,如图所示。实验时,保持桌面水平,用手轻推一下小车。在小车运动过程中,滴水计时器等时间间隔地滴下小水滴,图记录了桌面上连续的6个水滴的位置。已知滴水计时器每30s内共滴下46个小水滴
由图可知,小车在桌面上是_________填“从右向左”或“从左向右”运动的。
该小组同学根据图的数据判断出小车做匀变速运动。小车运动到图中A点位置时的速度大小为_______,加速度大小为_______。结果均保留2位有效数字
如图所示为实验中小车在重物牵引下得到的一条纸带,相邻计数点间有四个点未标出,打点计时器所接电源的频率为50Hz,则打B点时小车的速度大小为______,小车的加速度大小为______。保留三位有效数字
三、计算题(本大题共4小题,写出必理论根据和主要方程式,每小题各10分,共40分)
一辆汽车在平直的公路上以的速度行驶,刹车后开始做匀减速运动,加速度大小为从刹车开始计时,试求:
汽车还能运动的时间t;
汽车能通过的最大距离x;
汽车在前4秒内平均速度.
某一长直的赛道上,有一辆F1赛车前方200m有一安全车正以的速度匀速前进,此时赛车从静止出发以的加速度追赶.试求:
赛车追上安全车之前两车相距的最远距离多少?
赛车经过多长时间追上安全车?
赛车追上安全车时的速度为多少?
一辆汽车以的加速度由静止开始加速直线行驶。
时该汽车的速度大小是多少
如果此汽车以同样的加速度从的速度开始匀减速行驶,问
末汽车的速度大小是多少?
内此汽车的位移大小是多少
一个质点做匀加速直线运动,在相邻的两个1s内通过的位移分别为和。试求:
该质点的加速度大小a;
该质点在这两个1s末的瞬时速度和的大小。
参考答案
1.
A
解析取初速度方向为正方向,则,,根据速度时间关系可知,汽车做匀减速运动的时间为:,故刹车后6s内的位移实为刹车后匀减速运动4s内的位移,此时速度已经减速到零,所以位移为:,故A正确,故BCD错误。故选A。??
2.
D解析从静止开始的匀加速直线运动,则加速度a恒定不变,D图错误;,A图正确;,B图正确;,故C图正确。
本题选错误选项,故选D??
3.
B
解析根据可知,初速度,加速度。
刹车后做匀减速运动的位移为刹车痕迹长度:,故ADC错误,B正确。故选B。??
4.
B
解析由匀变速运动规律,结合图象可知,,加速度,得,由,知,故B正确,ACD错误。
故选B。??
5.
D
解析A.内,若运动员做匀加速运动,平均速度为,根据图像的“面积”等于位移可知,运动员的位移大于匀加速运动的位移,所以由公式,得知:内的平均速度大于匀加速运动的平均速度,故A错误;
B.由图知,15s末开始运动员做匀速直线运动,故B错误;
C.由图速度正负看出,运动员的速度一直沿正向,速度方向没有改变,故C错误;
D.图像的斜率减小,则其加速度减小,故运动员做加速度减小的减速运动,故D正确。故选D。??
6.C
解析根据和可知,速度只有在初速度为零的情况下,与时间成正比,位移只有在初速度为零时,与时间的平方成正比,故AB错误;
C.由可知,a一定,则物体的速度在一定时间内发生的变化与这段时间成正比,故C正确;
D.当物体做匀减速运动时,速度减小但位移可以增大,故D错误。故选:C。??
7.
BCD
解析AB、根据得,,故A错误,B正确;
C、物体在前4s内的位移,故C正确;
D、物体2s末的速度是?,故D正确。故选:BCD。??
8.
BD
解析A.由图读出,兔子和乌龟是从同地不同时刻出发的,兔子在乌龟出发后时间出发,故A错误;
B.在和两个时刻,兔子和乌龟位移相同,两者相遇,说明兔子和乌龟在比赛途中相遇过两次,故B正确;
C.乌龟做的是匀速直线运动,兔子先做匀速直线运动,在时间内静止不动,时刻以后又沿原方向做匀速直线运动,兔子不是沿着折线跑的,故C错误;
D.由图看出,时刻乌龟到达终点,而兔子还没有到达终点,说明乌龟先通过预定位移到达终点,故D正确。
故选BD。
9.
BC
解析设加速阶段的末速度为v,则加速阶段的加速度大小为,减速阶段的加速度大小,则加速度大小之比为1:2,故AD错误;
B.根据匀变速直线运动的平均速度公式得,加速阶段和减速阶段的平均速度之比为1:1,故B正确;
C.根据,知加速阶段和减速阶段的位移之比为2:1,故C正确。
故选BC。
10.AC
解析根据加速度图象中图线切线的斜率表示加速度大小,则有甲做匀加速运动,乙的加速度逐渐减小,在阶段,对乙图作切线,能找到一条与甲图线平行,即某时刻甲、乙加速度相等?,选项B错误,选项A、C正确;
D.因不知道两车初位置,故T时刻两者速度相等,不一定相遇,选项D错误。
故选AC。??
11.
BC
解:A、B、质点做直线运动的位移x与时间t的关系为;根据匀变速直线运动的位移时间关系公式,可得初速度,加速度;故A错误,B正确;
C、时的位置坐标为零;2s内的位移为:;故C正确;
D、2s末的速度为:;故D错误;
故选:BC。
12.AC
解析:A、匀变速直线运动某段时间内的平均速度等于这段时间内的初速度与末速度和的一半,故A正确.
B、由可知,只有连续相等的时间内位移的变化相等,可知B不正确.
C、由,a是常数,可知在任意相等的时间内速度的变化相等,故C正确;
D、某段时间内的平均速度,等于时间中点的瞬时速度;故D错误;
故选:AC
13.答案:从右向左;,。
解析
:由于用手轻推一下小车,则小车做减速运动,根据桌面上连续6个水滴的位置,可知,小车从右向左做减速运动;
已知滴水计时器每30s内共滴下46个小水滴,
那么各点时间间隔为:
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,有:
,
根据匀变速直线运动的推论公式可以求出加速度,得:
?,
那么加速度的大小为。
故答案为:从右向左;,。??
14.答案:?
解析:相邻计数点间有四个点未标出,打点计时器所接电源的频率为50Hz,相邻计数点间的时间间隔为,根据推论匀变速直线运动中,某段时间内的平均速度等于中间时刻的瞬时速度可知B点时小车的速度;
由逐差法公式可得
故答案为:;。
15.解:汽车还能运动的时间:
汽车能通过的最大距离:
汽车在前4秒内的位移:
平均速度:。
16.解:当两车速度相等时相距最远,由速度关系得:
解得:
即经过5s两车相距最远。当两车相距最远时,赛车位移:
安全车位移:
两车之间距离赛
解得:
设赛车经过时间t追上安全车,则有:
解得:
赛车追上安全车的速度是
赛车追上安全车时的速度为
17.解:时该汽车的速度
汽车停下用时
末汽车的速度
内汽车已停下,位移
18.解:由匀变速直线运动的推论:可知,加速度:;
质点的速度:,
速度:;
答:该质点的加速度大小a为;
该质点在这两个1s末的瞬时速度和的大小分别为:、
