4.1.1成比例线段(1) 课件 -2021—2022学年北师大版九年级数学上册(49张)
文档属性
| 名称 | 4.1.1成比例线段(1) 课件 -2021—2022学年北师大版九年级数学上册(49张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 22:27:55 | ||
图片预览








文档简介
(共49张PPT)
4.1成比例线段
数学(北师大版)
九年级
上册
第四章
图形的相似
学习目标
1.知道线段的比的概念,会计算两条线段的比;
2.理解成比例线段的概念;掌握成比例线段的判定方法.
3.理解比例的基本性质及其应用。
导入新课
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
讲授新课
如图,用同一张底片洗出的不同尺寸的照片中,汽车的形状还相同吗?大小呢?
下面图形有什么相同和不同的地方?
图形的放大与缩小
一
相同点:形状相同
不同点:大小不相同
图形的放大
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
图形的缩小
两个图形相似
图形的缩小
归纳:
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
思考:
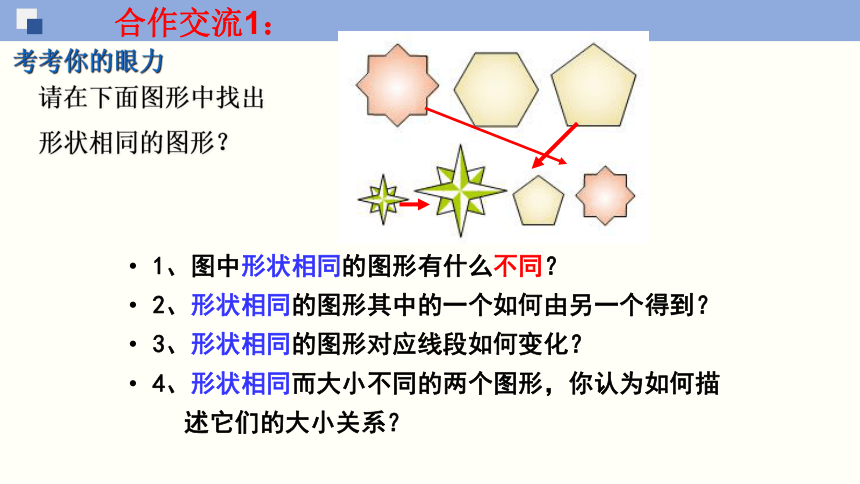
1、图中形状相同的图形有什么不同?
2、形状相同的图形其中的一个如何由另一个得到?
3、形状相同的图形对应线段如何变化?
4、形状相同而大小不同的两个图形,你认为如何描
述它们的大小关系?
合作交流1:
请在下面图形中找出
形状相同的图形?
考考你的眼力
讲授新课
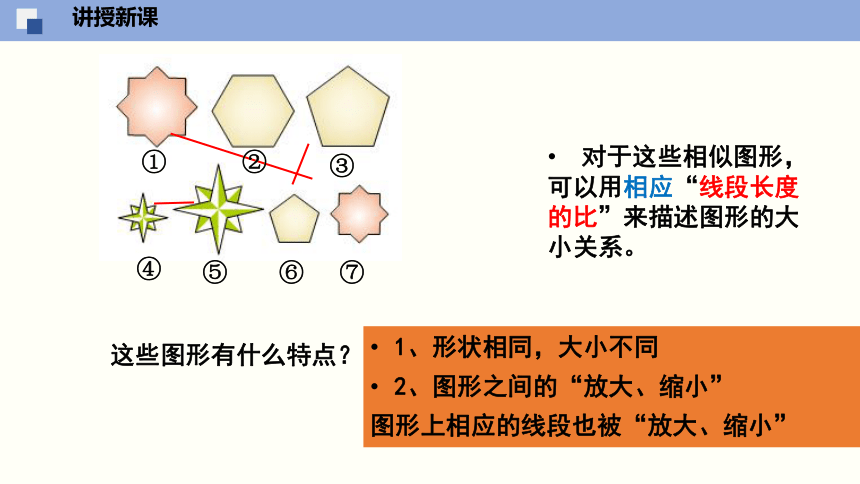
这些图形有什么特点?
对于这些相似图形,可以用相应“线段长度的比”来描述图形的大小关系。
1、形状相同,大小不同
2、图形之间的“放大、缩小”
图形上相应的线段也被“放大、缩小”
①
②
③
④
⑤
⑥
⑦
讲授新课
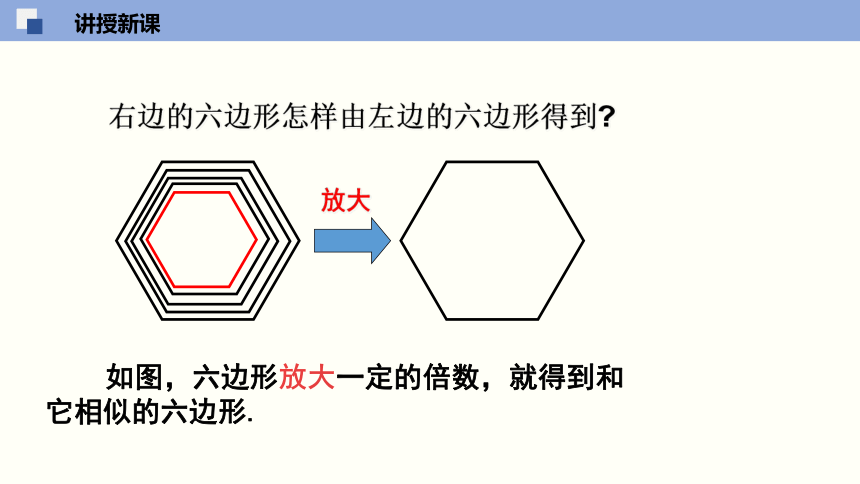
放大
右边的六边形怎样由左边的六边形得到?
如图,六边形放大一定的倍数,就得到和它相似的六边形.
讲授新课
缩小
右边的六边形怎样由左边的六边形得到?
如图,把六边形缩小一定的倍数就得到和它相似的六边形.
所以研究相似图形,先要学习线段的比和比例线段的有关知识.
讲授新课
如果选用 量得两条线段AB,CD的长度分别是m、n,那么这两条线段的比就是两条线段的长度比。
其中,AB、CD分别叫做这个线段比的前项、后项。
A
B
C
D
m
n
同一个长度单位
如果把
表示成比值k,
那么
,或
线段的比
一
讲授新课
1.若线段AB=6cm,CD=4cm,则
。
2.若线段AB=8cm,CD=2dm,则
。
巩固练习
练习:
讲授新课
如图所示,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上.
(1)AB,AD,EF,EH的长度分别是多少?
M
AB=_______
AD=_______
EF=_______
EH=_______
做一做
成比例线段
二
讲授新课
(2)计算
的值,你发现了什么?
则AB,EF,AD,EH是成比例线段,
AB,AD,EF,EH也是成比例线段。
讲授新课
已知四条线段a、b、c、d
中,如果其中两条线段的长度的比与另两条线段的长度的比相等,
那么
a、b、c、d
叫做成比例线段,简称比例线段。
即
(或
a
:
b=c
:
d
),
a
:
b
=
c
:
d
比例内项
比例外项
比例是指四条线段之间的一种关系,它们的排列是有顺序要求的。
a
:
b
=
c
:
d
d
叫做a、b、c的第四比例项
讲授新课
1.两条线段的比是一个正数,它没有单位;
注意事项:
3.线段的比要统一单位长度。
2.两条线段比与单位无关;
4.两条线段的比是有顺序的;
想一想:
1、两条线段的比和比例线段有什么区别和联系?
2、四条线段成比例与这四条线段的排列顺序有关吗?
归纳:线段的比是指
条线段之间的比的关系,而
比例线段是指
条线段间的关系.若两条线段的比
另两条线段的比,则这四条线段叫做
.
两
四
等于
成比例线段
四条线段成比例与这四条线段的排列顺序有关.
3.比例线段的概念是什么?如何判定四条线段成比例线段?它一般有哪些步骤?
概念:四条线段a,b,c,d,如果
(或a:b=c:d),那么这四条线段a,b,c,d叫比例线段。
方法有三:把四条线段按从小到大或从大到小的顺序排列好以后,①
②
③
步骤:一排(排顺序)二算(算比值或乘积)三判(判断是否成比例)
讲授新课
1.判断下列a、b、c、d是否成比例线段,为什么?
不成比例线段
成比例线段
2.判断下列各组线段是否成比例线段,为什么?
成比例线段
不成比例线段
3.下列各组线段中成比例线段的是( )
C
练习:
巩固练习
讲授新课
1.计算下列比例式的两个内项的积与两个内外项的积.
通过计算,你发现了什么规律?
两个内项的积与两个外项的积相等.
比例的基本性质
三
讲授新课
比例的基本性质
两外项之积=两内项之积。
交叉相乘积相等
思考:如果
,用什么方法说明两个内项的积与两个外项的积相等?
1.如果a、b、c、d
四个数成比例,即
,那么ad=bc
2.如果ad=bc(a,b,c,d都不等于0),那么
讲授新课
如果
,那么ad=bc.
证法一:等式
两边同时乘bd.
证法二:设
=k,则a=bk,c=dk,因此ad=(bk)d=b(dk)=bc.
如果ad=bc,怎么证明
?
等式两边同时除以bd.
注意:由ad=bc,得出
是有条件的,
即a,b,c,d都不等于0
讲授新课
你能由
推导出下列比例式吗?
左
右
右
左
右
左
左
右
a
b
c
d
=
b
c
b
c
b
a
d
c
=
b
d
a
c
=
c
d
a
b
=
c
d
b
c
a
=
b
c
a
c
b
d
=
c
b
c
b
c
c
a
d
b
=
c
b
d
c
b
a
=
c
b
ad=bc
对调内项或对调外项,比例仍成立!
1.如果-2x=5y,那么
C
针对练习
讲授新课
讲授新课
例1
一块矩形绸布的长AB=a
m,宽AD=1
m,按照图中所示方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即
那么a的值应当是多少?
解:根据题意可知,
AB=a
m
,
AE=
m,AD=1
m.
由
得
∴
B
C
E
F
D
A
当堂检测
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比
为(
)
A.100:3
B.1:3
C.10:3
D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例尺为(
)
A.5:1
B.
1:5
C.1:500000
D.500000:1
A
C
当堂检测
解:根据题意可知,
,
AB
=
15
,
AC
=
10
,
BD
=
6.
则
AD
=
AB
–
BD
=15
–
6=
9.
则
3.已知
,AB=15,AC=10,BD=6.求AE.
A
B
C
D
E
课堂小结
成比例线段
如果选用同一长度单位量得两条线段AB,CD的长
度分别是m,n,那么这两条线段的比就是它们长
度的比,即AB:CD=m:n,或写成
四条线段a,b,c,d,如果a与b的比等于c与d的
比,即
,那么这四条线段a,b,c,d叫做
成比例线段,简称比例线段.
线段的比
成比例线段
比例性质
新知导入
如图,已知
,你能求出
的值吗?
如果
,那么
有怎样的关系?在求解过程中,
你有什么发现?
【思考】比例的基本性质
方法1
令
(或者
)
方法2
等式两边同时加1(或者减1)
问题:已知,a、b、c、d、e、f
六个数,如果
,那么
和
成立吗?为什么?
成立。
由等式的性质就可以证明,在
的两边同时加上或减去1就行了。
比例的合比与分比性质:
如果
,那么
合比与分比性质
合分比性质:
如果
,那么
等比性质
如图,已知
,你能求出
的值吗?
由此你能得到什么样的结论?
解:∵
∴
AB=2HE,BC=2EF,CD=2FG,AD=2HG.
∴
∴
设
,则
a=kb,c=kd,e=kf,
所以
等比性质
由此可得到比例的又一性质:
此性质称为比例的等比性质,可以这样记忆:如果有n个数成比例,只要分母之和不为零,那么
。
等比性质
比例
性质
总结
例1:在△ABC与△DEF中,已知
,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB
+
BC
+
CA)=3(DE
+
EF
+
FD).
即
AB+BC+CA
=
(DE+EF+FD)
,
又
△ABC的周长为18cm,
即
AB+BC+CA=18cm.
∴
△DEF的周长为24cm.
等比性质应用
例2:若a,b,c都是不等于零的数,且
,求k的值.
解:当a+b+c≠0时,由
,
得
,
则k=2;
当a+b+c=0时,则有a+b=-c.
此时
综上所述,k的值是2或-1.
等比性质应用
易错点
课堂练习
1、已知
,
的值。
2、小明认为:
(1)如果
那么
。
(2)如果
,那么
。
这两个结论正确吗?为什么?
(1)?
(2)?
合比性质的应用
2、(1)证明:∵
∴
在等式两边同时加ac
即
∵
在等式两边同时除以
即
∴
3.(1)已知
,那么
=
,
=
.
(2)如果
那么
.
(3)如果
,那么
.
4.已知a:b:c=2:3:5,求
的值。
解:设
则
a=2k,b=3k,c=5k
∴
∴
方法提炼:
当题目中出现等比的形式时,我们通常用设参数法来解决此类问题,利用参数作为中间的“桥梁”,在题设中增设参数k,然后在解题的过程中参数k自然消失,从而最终解决问题。
课堂练习
1.若
A.1
B.2
C.3
D.4
B
C
2.
若x:y:z=2:3:7,且x-y+3=z-2y,则z的值为(
)
A.7
B.63
C.10.5
D.6.75
拓展提高
1、一个多边形的边长为2、3、4、5、6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边是(
)
A、
6
B、8
C、10
D、12
2、已知相似的两个矩形中,一个矩形的长和面积分别是4和12,
另一个矩形的宽是6,求这两个矩形的面积比。(
)
1、B
2、4:1
谢谢~
4.1成比例线段
数学(北师大版)
九年级
上册
第四章
图形的相似
学习目标
1.知道线段的比的概念,会计算两条线段的比;
2.理解成比例线段的概念;掌握成比例线段的判定方法.
3.理解比例的基本性质及其应用。
导入新课
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
讲授新课
如图,用同一张底片洗出的不同尺寸的照片中,汽车的形状还相同吗?大小呢?
下面图形有什么相同和不同的地方?
图形的放大与缩小
一
相同点:形状相同
不同点:大小不相同
图形的放大
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
图形的缩小
两个图形相似
图形的缩小
归纳:
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
思考:
1、图中形状相同的图形有什么不同?
2、形状相同的图形其中的一个如何由另一个得到?
3、形状相同的图形对应线段如何变化?
4、形状相同而大小不同的两个图形,你认为如何描
述它们的大小关系?
合作交流1:
请在下面图形中找出
形状相同的图形?
考考你的眼力
讲授新课
这些图形有什么特点?
对于这些相似图形,可以用相应“线段长度的比”来描述图形的大小关系。
1、形状相同,大小不同
2、图形之间的“放大、缩小”
图形上相应的线段也被“放大、缩小”
①
②
③
④
⑤
⑥
⑦
讲授新课
放大
右边的六边形怎样由左边的六边形得到?
如图,六边形放大一定的倍数,就得到和它相似的六边形.
讲授新课
缩小
右边的六边形怎样由左边的六边形得到?
如图,把六边形缩小一定的倍数就得到和它相似的六边形.
所以研究相似图形,先要学习线段的比和比例线段的有关知识.
讲授新课
如果选用 量得两条线段AB,CD的长度分别是m、n,那么这两条线段的比就是两条线段的长度比。
其中,AB、CD分别叫做这个线段比的前项、后项。
A
B
C
D
m
n
同一个长度单位
如果把
表示成比值k,
那么
,或
线段的比
一
讲授新课
1.若线段AB=6cm,CD=4cm,则
。
2.若线段AB=8cm,CD=2dm,则
。
巩固练习
练习:
讲授新课
如图所示,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上.
(1)AB,AD,EF,EH的长度分别是多少?
M
AB=_______
AD=_______
EF=_______
EH=_______
做一做
成比例线段
二
讲授新课
(2)计算
的值,你发现了什么?
则AB,EF,AD,EH是成比例线段,
AB,AD,EF,EH也是成比例线段。
讲授新课
已知四条线段a、b、c、d
中,如果其中两条线段的长度的比与另两条线段的长度的比相等,
那么
a、b、c、d
叫做成比例线段,简称比例线段。
即
(或
a
:
b=c
:
d
),
a
:
b
=
c
:
d
比例内项
比例外项
比例是指四条线段之间的一种关系,它们的排列是有顺序要求的。
a
:
b
=
c
:
d
d
叫做a、b、c的第四比例项
讲授新课
1.两条线段的比是一个正数,它没有单位;
注意事项:
3.线段的比要统一单位长度。
2.两条线段比与单位无关;
4.两条线段的比是有顺序的;
想一想:
1、两条线段的比和比例线段有什么区别和联系?
2、四条线段成比例与这四条线段的排列顺序有关吗?
归纳:线段的比是指
条线段之间的比的关系,而
比例线段是指
条线段间的关系.若两条线段的比
另两条线段的比,则这四条线段叫做
.
两
四
等于
成比例线段
四条线段成比例与这四条线段的排列顺序有关.
3.比例线段的概念是什么?如何判定四条线段成比例线段?它一般有哪些步骤?
概念:四条线段a,b,c,d,如果
(或a:b=c:d),那么这四条线段a,b,c,d叫比例线段。
方法有三:把四条线段按从小到大或从大到小的顺序排列好以后,①
②
③
步骤:一排(排顺序)二算(算比值或乘积)三判(判断是否成比例)
讲授新课
1.判断下列a、b、c、d是否成比例线段,为什么?
不成比例线段
成比例线段
2.判断下列各组线段是否成比例线段,为什么?
成比例线段
不成比例线段
3.下列各组线段中成比例线段的是( )
C
练习:
巩固练习
讲授新课
1.计算下列比例式的两个内项的积与两个内外项的积.
通过计算,你发现了什么规律?
两个内项的积与两个外项的积相等.
比例的基本性质
三
讲授新课
比例的基本性质
两外项之积=两内项之积。
交叉相乘积相等
思考:如果
,用什么方法说明两个内项的积与两个外项的积相等?
1.如果a、b、c、d
四个数成比例,即
,那么ad=bc
2.如果ad=bc(a,b,c,d都不等于0),那么
讲授新课
如果
,那么ad=bc.
证法一:等式
两边同时乘bd.
证法二:设
=k,则a=bk,c=dk,因此ad=(bk)d=b(dk)=bc.
如果ad=bc,怎么证明
?
等式两边同时除以bd.
注意:由ad=bc,得出
是有条件的,
即a,b,c,d都不等于0
讲授新课
你能由
推导出下列比例式吗?
左
右
右
左
右
左
左
右
a
b
c
d
=
b
c
b
c
b
a
d
c
=
b
d
a
c
=
c
d
a
b
=
c
d
b
c
a
=
b
c
a
c
b
d
=
c
b
c
b
c
c
a
d
b
=
c
b
d
c
b
a
=
c
b
ad=bc
对调内项或对调外项,比例仍成立!
1.如果-2x=5y,那么
C
针对练习
讲授新课
讲授新课
例1
一块矩形绸布的长AB=a
m,宽AD=1
m,按照图中所示方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即
那么a的值应当是多少?
解:根据题意可知,
AB=a
m
,
AE=
m,AD=1
m.
由
得
∴
B
C
E
F
D
A
当堂检测
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比
为(
)
A.100:3
B.1:3
C.10:3
D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例尺为(
)
A.5:1
B.
1:5
C.1:500000
D.500000:1
A
C
当堂检测
解:根据题意可知,
,
AB
=
15
,
AC
=
10
,
BD
=
6.
则
AD
=
AB
–
BD
=15
–
6=
9.
则
3.已知
,AB=15,AC=10,BD=6.求AE.
A
B
C
D
E
课堂小结
成比例线段
如果选用同一长度单位量得两条线段AB,CD的长
度分别是m,n,那么这两条线段的比就是它们长
度的比,即AB:CD=m:n,或写成
四条线段a,b,c,d,如果a与b的比等于c与d的
比,即
,那么这四条线段a,b,c,d叫做
成比例线段,简称比例线段.
线段的比
成比例线段
比例性质
新知导入
如图,已知
,你能求出
的值吗?
如果
,那么
有怎样的关系?在求解过程中,
你有什么发现?
【思考】比例的基本性质
方法1
令
(或者
)
方法2
等式两边同时加1(或者减1)
问题:已知,a、b、c、d、e、f
六个数,如果
,那么
和
成立吗?为什么?
成立。
由等式的性质就可以证明,在
的两边同时加上或减去1就行了。
比例的合比与分比性质:
如果
,那么
合比与分比性质
合分比性质:
如果
,那么
等比性质
如图,已知
,你能求出
的值吗?
由此你能得到什么样的结论?
解:∵
∴
AB=2HE,BC=2EF,CD=2FG,AD=2HG.
∴
∴
设
,则
a=kb,c=kd,e=kf,
所以
等比性质
由此可得到比例的又一性质:
此性质称为比例的等比性质,可以这样记忆:如果有n个数成比例,只要分母之和不为零,那么
。
等比性质
比例
性质
总结
例1:在△ABC与△DEF中,已知
,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB
+
BC
+
CA)=3(DE
+
EF
+
FD).
即
AB+BC+CA
=
(DE+EF+FD)
,
又
△ABC的周长为18cm,
即
AB+BC+CA=18cm.
∴
△DEF的周长为24cm.
等比性质应用
例2:若a,b,c都是不等于零的数,且
,求k的值.
解:当a+b+c≠0时,由
,
得
,
则k=2;
当a+b+c=0时,则有a+b=-c.
此时
综上所述,k的值是2或-1.
等比性质应用
易错点
课堂练习
1、已知
,
的值。
2、小明认为:
(1)如果
那么
。
(2)如果
,那么
。
这两个结论正确吗?为什么?
(1)?
(2)?
合比性质的应用
2、(1)证明:∵
∴
在等式两边同时加ac
即
∵
在等式两边同时除以
即
∴
3.(1)已知
,那么
=
,
=
.
(2)如果
那么
.
(3)如果
,那么
.
4.已知a:b:c=2:3:5,求
的值。
解:设
则
a=2k,b=3k,c=5k
∴
∴
方法提炼:
当题目中出现等比的形式时,我们通常用设参数法来解决此类问题,利用参数作为中间的“桥梁”,在题设中增设参数k,然后在解题的过程中参数k自然消失,从而最终解决问题。
课堂练习
1.若
A.1
B.2
C.3
D.4
B
C
2.
若x:y:z=2:3:7,且x-y+3=z-2y,则z的值为(
)
A.7
B.63
C.10.5
D.6.75
拓展提高
1、一个多边形的边长为2、3、4、5、6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边是(
)
A、
6
B、8
C、10
D、12
2、已知相似的两个矩形中,一个矩形的长和面积分别是4和12,
另一个矩形的宽是6,求这两个矩形的面积比。(
)
1、B
2、4:1
谢谢~
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
