第2章 对称图形——圆检测卷(2)2021--2022学年苏科版九年级数学上册(word版无答案)
文档属性
| 名称 | 第2章 对称图形——圆检测卷(2)2021--2022学年苏科版九年级数学上册(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 22:28:04 | ||
图片预览


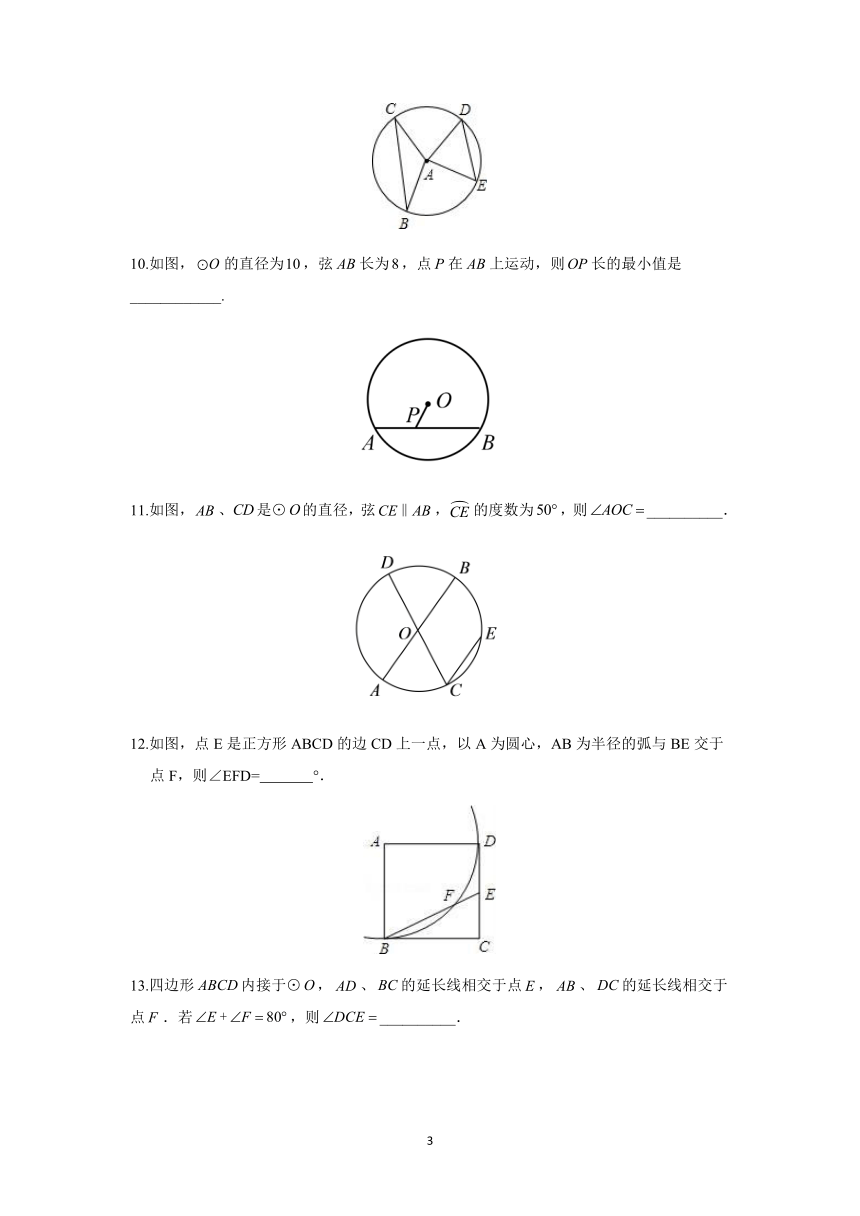
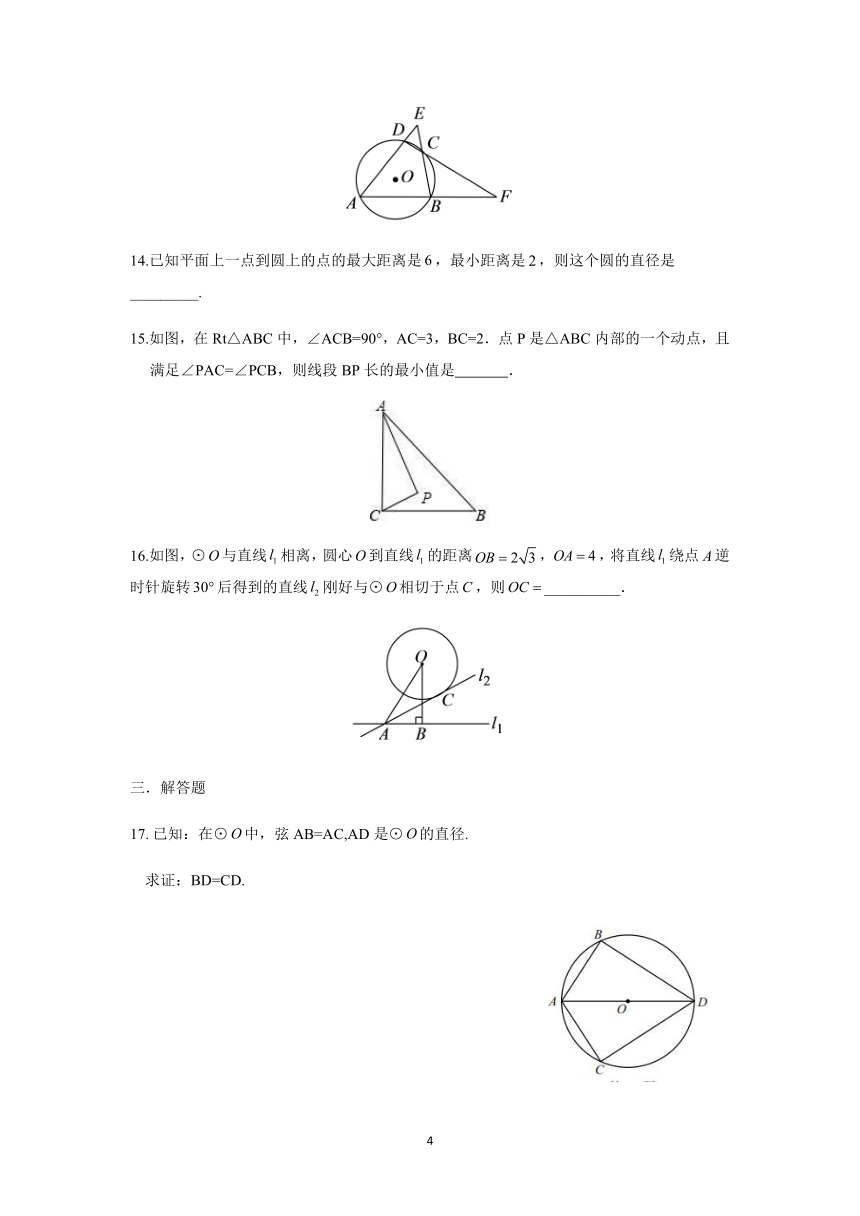
文档简介
2021年苏科版对称图形——圆单元测试(二)(无答案)
一.选择题
1.已知⊙的半径为,点为的中点,则当时,点与⊙的位置关系是(
).
点在圆内
B.
点在圆上
C.
点圆上
D.
不能确定
2.如图,在半径为的⊙中,弦,于点,则长为().
B.
C.
D.
3.如图,是半圆的直径,是的中点,,则等于(
)
A.
B.
C.
D.
4.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13
B.12
C.11
D.10
5.如图,为直径,作弦,的平分线交于点,当点在下半圆上移动时,(不与点、重合),下列关于点描述正确的是(
)
A.到的距离保持不变
B.到点距离保持不变
C.等分
D.位置不变
6.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于E,F,G三点,过点D作☉O的切线交BC于点M,切点为N,则DM的长为(
?
)
B.
C.
D.
填空题
7.若一个圆锥的底面半径是,母线长是,则其侧面展开图的面积是______.(结果保留)
8.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=
米.(精确到0.01米)
9.如图,圆A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于
.
10.如图,的直径为,弦长为,点在上运动,则长的最小值是____________.
11.如图,、是⊙的直径,弦,的度数为,则__________.
12.如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=
°.
13.四边形内接于⊙,、的延长线相交于点,、的延长线相交于点.若,则__________.
14.已知平面上一点到圆上的点的最大距离是,最小距离是,则这个圆的直径是_________.
15.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=2.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是
.
16.如图,⊙与直线相离,圆心到直线的距离,,将直线绕点逆时针旋转后得到的直线刚好与⊙相切于点,则__________.
解答题
已知:在⊙中,弦AB=AC,AD是⊙的直径.
求证:BD=CD.
已知,如图,OC是⊙O的半径,AB是弦,OC⊥AB于D,AB=8,OD=CD+1,求⊙O的半径.
19.如图所示,破残的圆形轮片上,弦的垂直平分线交于点,交弦于点.
(1)求作此轮片所在的;
(2)若此轮片的半径为,,求的长.
20.△ABC
是⊙O
的内接三角形,AB=AC,⊙O
的半径为
2,O
到
BC
的距
离为
1.
(1)求
BC
的长;
(2)∠BAC
的度数为
°.
21.如图,是半圆的直径,和是它的两条切线,切点分别为、,平分.
()求证:是半圆的切线.
()若,,求的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)若DE+EA=4,⊙O的半径为5,求CF的长度.
23.四边形、都是的内接四边形,,,与交于点.
求证:.
为了证明结论,小明进行了探索,请在下列框图中补全他的证明思路:
小明的证明思路
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC=6.
(1)用尺规作⊙O,使它分别与射线AB、AC相切于点B、C;
(2)求的长.
25.如图,在中,为边的中点,是上一点,与相切于点,且与、分别相交于点、.连接交于点.
(1)求证:.
(2)已知,,当是的直径时,求的长.
26.在学习圆上这一节时,小丽遇到了一个问题:
如图,,,试说明点、、、在同一个圆上.
小丽想到了一个方法,如图,取的中点,连接、,利用直角三角形的某性质,要到,进行说明了点、、在以点为圆心的同一个圆上.
()小明利用的直角三角形的性质____________.
()在如图的四边形中,若,则点、、、在同一个圆上吗?请说明理由.
()根据上一题的经验,请解决如下问题:如图,中,三条高,,相交于点,连接,,,试说明平分.
一.选择题
1.已知⊙的半径为,点为的中点,则当时,点与⊙的位置关系是(
).
点在圆内
B.
点在圆上
C.
点圆上
D.
不能确定
2.如图,在半径为的⊙中,弦,于点,则长为().
B.
C.
D.
3.如图,是半圆的直径,是的中点,,则等于(
)
A.
B.
C.
D.
4.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13
B.12
C.11
D.10
5.如图,为直径,作弦,的平分线交于点,当点在下半圆上移动时,(不与点、重合),下列关于点描述正确的是(
)
A.到的距离保持不变
B.到点距离保持不变
C.等分
D.位置不变
6.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于E,F,G三点,过点D作☉O的切线交BC于点M,切点为N,则DM的长为(
?
)
B.
C.
D.
填空题
7.若一个圆锥的底面半径是,母线长是,则其侧面展开图的面积是______.(结果保留)
8.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=
米.(精确到0.01米)
9.如图,圆A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于
.
10.如图,的直径为,弦长为,点在上运动,则长的最小值是____________.
11.如图,、是⊙的直径,弦,的度数为,则__________.
12.如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=
°.
13.四边形内接于⊙,、的延长线相交于点,、的延长线相交于点.若,则__________.
14.已知平面上一点到圆上的点的最大距离是,最小距离是,则这个圆的直径是_________.
15.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=2.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是
.
16.如图,⊙与直线相离,圆心到直线的距离,,将直线绕点逆时针旋转后得到的直线刚好与⊙相切于点,则__________.
解答题
已知:在⊙中,弦AB=AC,AD是⊙的直径.
求证:BD=CD.
已知,如图,OC是⊙O的半径,AB是弦,OC⊥AB于D,AB=8,OD=CD+1,求⊙O的半径.
19.如图所示,破残的圆形轮片上,弦的垂直平分线交于点,交弦于点.
(1)求作此轮片所在的;
(2)若此轮片的半径为,,求的长.
20.△ABC
是⊙O
的内接三角形,AB=AC,⊙O
的半径为
2,O
到
BC
的距
离为
1.
(1)求
BC
的长;
(2)∠BAC
的度数为
°.
21.如图,是半圆的直径,和是它的两条切线,切点分别为、,平分.
()求证:是半圆的切线.
()若,,求的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)若DE+EA=4,⊙O的半径为5,求CF的长度.
23.四边形、都是的内接四边形,,,与交于点.
求证:.
为了证明结论,小明进行了探索,请在下列框图中补全他的证明思路:
小明的证明思路
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC=6.
(1)用尺规作⊙O,使它分别与射线AB、AC相切于点B、C;
(2)求的长.
25.如图,在中,为边的中点,是上一点,与相切于点,且与、分别相交于点、.连接交于点.
(1)求证:.
(2)已知,,当是的直径时,求的长.
26.在学习圆上这一节时,小丽遇到了一个问题:
如图,,,试说明点、、、在同一个圆上.
小丽想到了一个方法,如图,取的中点,连接、,利用直角三角形的某性质,要到,进行说明了点、、在以点为圆心的同一个圆上.
()小明利用的直角三角形的性质____________.
()在如图的四边形中,若,则点、、、在同一个圆上吗?请说明理由.
()根据上一题的经验,请解决如下问题:如图,中,三条高,,相交于点,连接,,,试说明平分.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
