人教版小学数学五年级上组合图形的面积同步练习(含答案)
文档属性
| 名称 | 人教版小学数学五年级上组合图形的面积同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 08:09:24 | ||
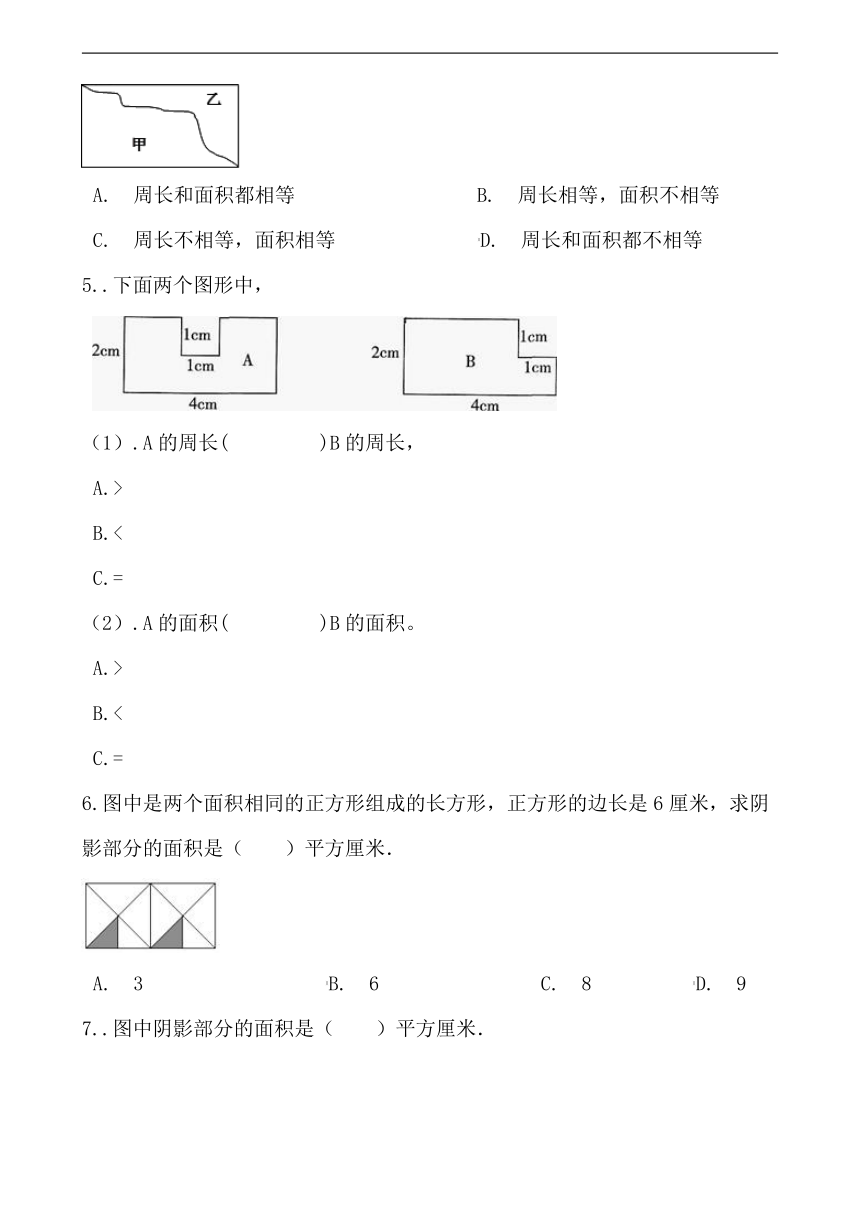
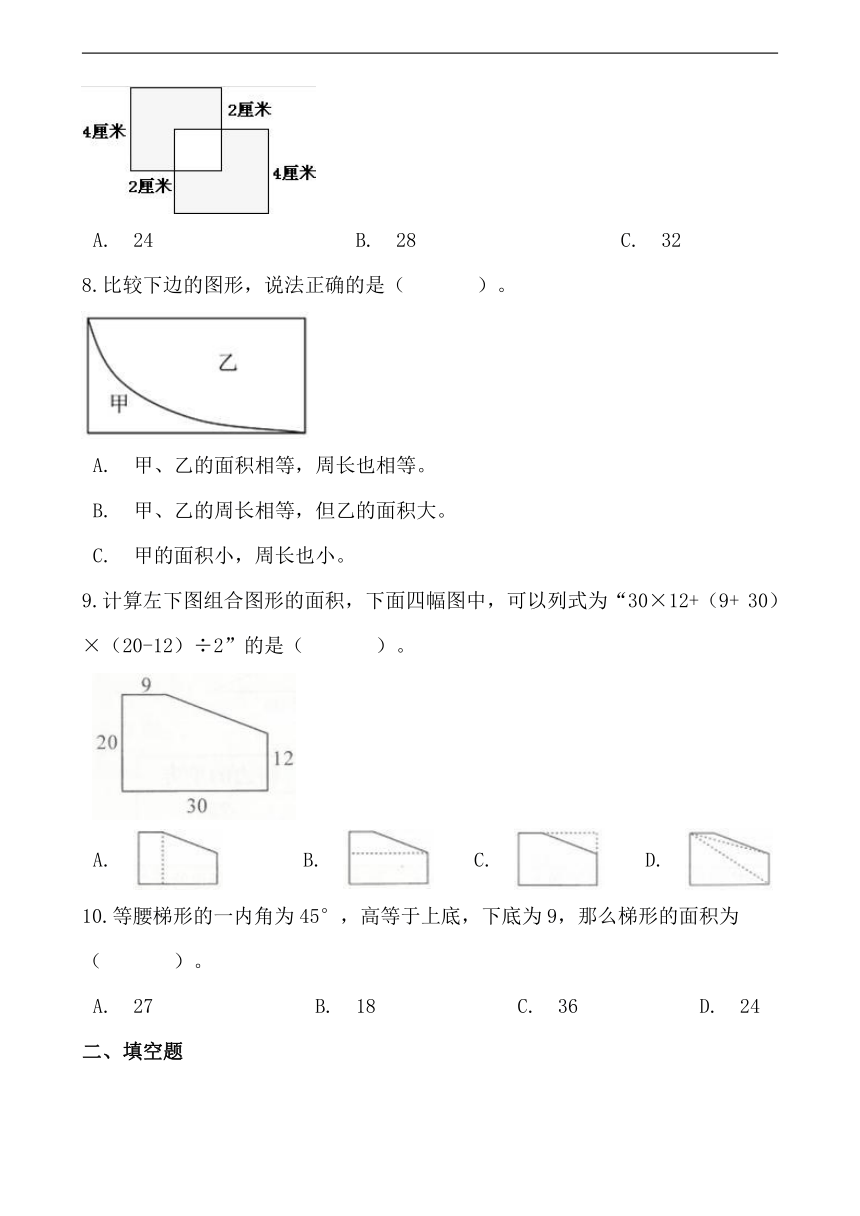
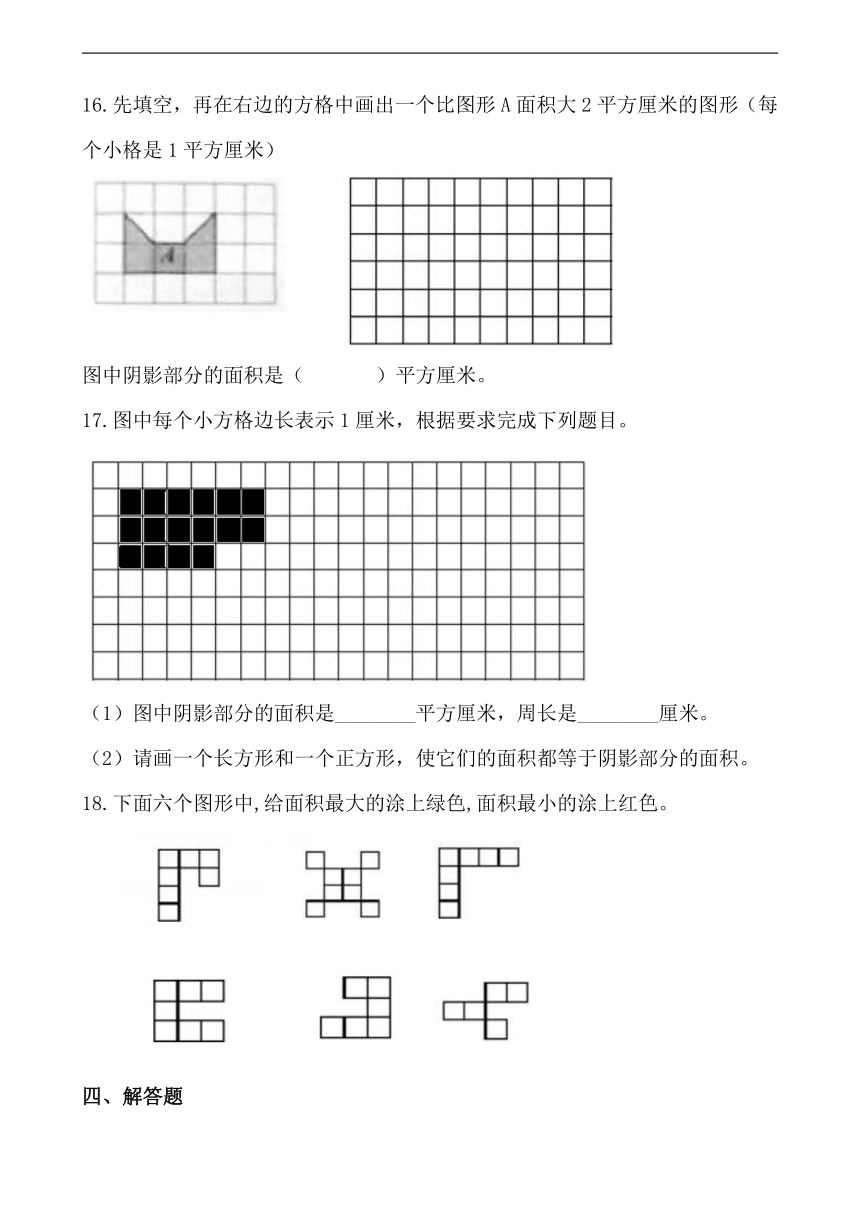
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版小学数学五年级上组合图形的面积同步练习
姓名:__________
班级:__________考号:__________
一、单选题
1.下面图形中,空白部分与阴影部分周长相等但面积不相等的是(????
)。
A.????B.???C.???D.?
2..如图
半径均为2cm的四个圆如图所示,分别连结
,
,
,
,所得正方形,则其阴影部分的面积为(??
)
A.?16-π?B.?16-2π??C.?16-3π??D.?16-4π
3..下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为(???
)cm2。
A.?20???????B.?24????????C.?28?????D.?32
4.下图中,长方形被分成甲、乙两部分,这两部分(???
)。
A.?周长和面积都相等?????????B.?周长相等,面积不相等
C.?周长不相等,面积相等?????
D.?周长和面积都不相等
5..下面两个图形中,
(1).A的周长(
????)B的周长,
A.>
B.<
C.=
(2).A的面积(
????)B的面积。
A.>
B.<
C.=
6.图中是两个面积相同的正方形组成的长方形,正方形的边长是6厘米,求阴影部分的面积是( )平方厘米.
A.?3?????????B.?6????????C.?8?????D.?9
7..图中阴影部分的面积是( )平方厘米.
A.?24??????????B.?28??????????C.?32
8.比较下边的图形,说法正确的是(???
)。
A.?甲、乙的面积相等,周长也相等。
B.?甲、乙的周长相等,但乙的面积大。
C.?甲的面积小,周长也小。
9.计算左下图组合图形的面积,下面四幅图中,可以列式为“30×12+(9+
30)×(20-12)÷2”的是(???
)。
A.?????B.???C.???D.?
10.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为(???
)。
A.?27????????B.?18???????C.?36??????D.?24
二、填空题
11.
以上两个图形________面积大
12..如图,阴影部分的面积和空白部分的面积比是5:7,正方形的边长是8厘米,DE的长是??????厘米.
13.估测下列图形的面积:
面积≈________
14.下列方格中,哪个图形面积大
15.用________原理对组合图形进行分割时,图形的面积大小________。
三、作图题
16.先填空,再在右边的方格中画出一个比图形A面积大2平方厘米的图形(每个小格是1平方厘米)
图中阴影部分的面积是(???
)平方厘米。
17.图中每个小方格边长表示1厘米,根据要求完成下列题目。
(1)图中阴影部分的面积是________平方厘米,周长是________厘米。
(2)请画一个长方形和一个正方形,使它们的面积都等于阴影部分的面积。
18.下面六个图形中,给面积最大的涂上绿色,面积最小的涂上红色。
四、解答题
19.求阴影部分的面积。(单位:厘米)
20.下图中,平行四边形的面积是40cm2
,
阴影部分是直角三角形,它的面积是多少平方厘米?
21.下图是两个正方形,求阴影部分的面积。
22.计算下图的面积。
23.求图形的面积。
24..求下面图形中阴影部分的面积.(先在图中量出并标出计算时需要的数据)
25.求下列图形的周长与面积:
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
D
3.【答案】
B
4.【答案】
B
5.【答案】
(1)A
(2)C
6.【答案】
D
7.【答案】
A
8.【答案】
B
9.【答案】
B
10.【答案】
B
二、填空题
11.【答案】
(1)
12.【答案】
13.【答案】
24
14.【答案】
一样大
15.【答案】
出入相补;不变
三、作图题
16.【答案】
解:图中阴影部分的面积是4平方厘米。
【解析】先将图中阴影部分的面积计算出来,然后将计算出的面积加2平方厘米,进而画出图形即可。
17.【答案】
(1)16;18
(2)解:如图所示:
【解析】(1)面积=16×1×1=16(平方厘米)
周长=(6+3)×2
=9×2
=18(厘米)
图中阴影部分的面积是16平方厘米,周长是18厘米。
18.【答案】
第二个最大,最后一个最小
【解析】根据分析可得:图形1的面积是7,
图形2的面积是8,图形3的面积是7,图形4的面积是7,图形5的面积是6,图形6的面积是5,据此作图如下:
四、解答题
19.【答案】
解:6×3-3×3÷2
=18-9÷2
=18-4.5
=13.5(平方厘米)
所以阴影部分的面积是13.5平方厘米。
【解析】将弓形阴影部分的面积平移,可得出图中阴影部分的面积=长方形的面积(长6厘米、宽3厘米)-三角形的面积(三角形的底和高分别是圆的半径),再根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数值计算即可。
20.【答案】
解:(40÷5-6)×5÷2
=2×5÷2
=5(平方厘米)
答:它的面积是5平方厘米。
【解析】阴影部分是三角形,它的高和平行四边形的高相等。用平行四边形面积除以高求出底,用底减去6厘米即可求出三角形的底,用三角形的底乘高再除以2即可求出阴影部分的面积。
21.【答案】
解:6×6+4×4
=36+16
=52(平方厘米)
6×6÷2
=36÷2
=18(平方厘米)
4+6=10(厘米)
10×4÷2
=40÷2
=20(平方厘米)
52-18-20
=34-20
=14(平方厘米)
【解析】阴影部分的面积=大正方形的面积+小正方形的面积-上边空白三角形的面积-下边空白三角形的面积;其中,正方形的面积=边长×边长,三角形的面积=底×高÷2。
22.【答案】
解:5×(6-3)+3×2
=5×3+6
=15+6
=21(平方厘米)
【解析】可以把图形分成左、右两个长方形分别计算面积,左边长方形的长是5厘米,宽
(6-3)厘米;长方形面积=长×宽,由此计算即可.
23.【答案】
解:50×33+35×12÷2
=1650+420÷2
=1650+210
=1860(m?)
【解析】组合图形的面积=平行四边形的面积+三角形的面积,其中平行四边形面积=底×高,三角形面积=底×高÷2,据此列式计算即可。
24.【答案】
解:如图所示,量得R=1.2厘米,r=1厘米,
则阴影部分的面积:3.14×(1.22﹣12),
=3.14×(1.44﹣1),
=3.14×0.44,
=1.3816(平方厘米);
答:阴影部分的面积是1.3816平方厘米
【解析】量出大小圆的半径的长度,即可用大圆的面积减去小圆的面积就是圆环的面积.此题主要考查圆环面积的计算方法
25.【答案】解:周长:(25+10)×2=70(cm),面积:10×25=250(
);
周长:(8+5+18)×2=62(dm),面积:8×18+5×6=174(
)
【解析】(1)周长:(25+10)×2
=35×2
=70(cm)
面积:10×25=250(
cm2
)
(2)周长:(8+5+18)×2
=(13+18)×2
=31×2
=62(dm)
面积:8×18+5×6
=144+30
=174(
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版小学数学五年级上组合图形的面积同步练习
姓名:__________
班级:__________考号:__________
一、单选题
1.下面图形中,空白部分与阴影部分周长相等但面积不相等的是(????
)。
A.????B.???C.???D.?
2..如图
半径均为2cm的四个圆如图所示,分别连结
,
,
,
,所得正方形,则其阴影部分的面积为(??
)
A.?16-π?B.?16-2π??C.?16-3π??D.?16-4π
3..下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为(???
)cm2。
A.?20???????B.?24????????C.?28?????D.?32
4.下图中,长方形被分成甲、乙两部分,这两部分(???
)。
A.?周长和面积都相等?????????B.?周长相等,面积不相等
C.?周长不相等,面积相等?????
D.?周长和面积都不相等
5..下面两个图形中,
(1).A的周长(
????)B的周长,
A.>
B.<
C.=
(2).A的面积(
????)B的面积。
A.>
B.<
C.=
6.图中是两个面积相同的正方形组成的长方形,正方形的边长是6厘米,求阴影部分的面积是( )平方厘米.
A.?3?????????B.?6????????C.?8?????D.?9
7..图中阴影部分的面积是( )平方厘米.
A.?24??????????B.?28??????????C.?32
8.比较下边的图形,说法正确的是(???
)。
A.?甲、乙的面积相等,周长也相等。
B.?甲、乙的周长相等,但乙的面积大。
C.?甲的面积小,周长也小。
9.计算左下图组合图形的面积,下面四幅图中,可以列式为“30×12+(9+
30)×(20-12)÷2”的是(???
)。
A.?????B.???C.???D.?
10.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为(???
)。
A.?27????????B.?18???????C.?36??????D.?24
二、填空题
11.
以上两个图形________面积大
12..如图,阴影部分的面积和空白部分的面积比是5:7,正方形的边长是8厘米,DE的长是??????厘米.
13.估测下列图形的面积:
面积≈________
14.下列方格中,哪个图形面积大
15.用________原理对组合图形进行分割时,图形的面积大小________。
三、作图题
16.先填空,再在右边的方格中画出一个比图形A面积大2平方厘米的图形(每个小格是1平方厘米)
图中阴影部分的面积是(???
)平方厘米。
17.图中每个小方格边长表示1厘米,根据要求完成下列题目。
(1)图中阴影部分的面积是________平方厘米,周长是________厘米。
(2)请画一个长方形和一个正方形,使它们的面积都等于阴影部分的面积。
18.下面六个图形中,给面积最大的涂上绿色,面积最小的涂上红色。
四、解答题
19.求阴影部分的面积。(单位:厘米)
20.下图中,平行四边形的面积是40cm2
,
阴影部分是直角三角形,它的面积是多少平方厘米?
21.下图是两个正方形,求阴影部分的面积。
22.计算下图的面积。
23.求图形的面积。
24..求下面图形中阴影部分的面积.(先在图中量出并标出计算时需要的数据)
25.求下列图形的周长与面积:
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
D
3.【答案】
B
4.【答案】
B
5.【答案】
(1)A
(2)C
6.【答案】
D
7.【答案】
A
8.【答案】
B
9.【答案】
B
10.【答案】
B
二、填空题
11.【答案】
(1)
12.【答案】
13.【答案】
24
14.【答案】
一样大
15.【答案】
出入相补;不变
三、作图题
16.【答案】
解:图中阴影部分的面积是4平方厘米。
【解析】先将图中阴影部分的面积计算出来,然后将计算出的面积加2平方厘米,进而画出图形即可。
17.【答案】
(1)16;18
(2)解:如图所示:
【解析】(1)面积=16×1×1=16(平方厘米)
周长=(6+3)×2
=9×2
=18(厘米)
图中阴影部分的面积是16平方厘米,周长是18厘米。
18.【答案】
第二个最大,最后一个最小
【解析】根据分析可得:图形1的面积是7,
图形2的面积是8,图形3的面积是7,图形4的面积是7,图形5的面积是6,图形6的面积是5,据此作图如下:
四、解答题
19.【答案】
解:6×3-3×3÷2
=18-9÷2
=18-4.5
=13.5(平方厘米)
所以阴影部分的面积是13.5平方厘米。
【解析】将弓形阴影部分的面积平移,可得出图中阴影部分的面积=长方形的面积(长6厘米、宽3厘米)-三角形的面积(三角形的底和高分别是圆的半径),再根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数值计算即可。
20.【答案】
解:(40÷5-6)×5÷2
=2×5÷2
=5(平方厘米)
答:它的面积是5平方厘米。
【解析】阴影部分是三角形,它的高和平行四边形的高相等。用平行四边形面积除以高求出底,用底减去6厘米即可求出三角形的底,用三角形的底乘高再除以2即可求出阴影部分的面积。
21.【答案】
解:6×6+4×4
=36+16
=52(平方厘米)
6×6÷2
=36÷2
=18(平方厘米)
4+6=10(厘米)
10×4÷2
=40÷2
=20(平方厘米)
52-18-20
=34-20
=14(平方厘米)
【解析】阴影部分的面积=大正方形的面积+小正方形的面积-上边空白三角形的面积-下边空白三角形的面积;其中,正方形的面积=边长×边长,三角形的面积=底×高÷2。
22.【答案】
解:5×(6-3)+3×2
=5×3+6
=15+6
=21(平方厘米)
【解析】可以把图形分成左、右两个长方形分别计算面积,左边长方形的长是5厘米,宽
(6-3)厘米;长方形面积=长×宽,由此计算即可.
23.【答案】
解:50×33+35×12÷2
=1650+420÷2
=1650+210
=1860(m?)
【解析】组合图形的面积=平行四边形的面积+三角形的面积,其中平行四边形面积=底×高,三角形面积=底×高÷2,据此列式计算即可。
24.【答案】
解:如图所示,量得R=1.2厘米,r=1厘米,
则阴影部分的面积:3.14×(1.22﹣12),
=3.14×(1.44﹣1),
=3.14×0.44,
=1.3816(平方厘米);
答:阴影部分的面积是1.3816平方厘米
【解析】量出大小圆的半径的长度,即可用大圆的面积减去小圆的面积就是圆环的面积.此题主要考查圆环面积的计算方法
25.【答案】解:周长:(25+10)×2=70(cm),面积:10×25=250(
);
周长:(8+5+18)×2=62(dm),面积:8×18+5×6=174(
)
【解析】(1)周长:(25+10)×2
=35×2
=70(cm)
面积:10×25=250(
cm2
)
(2)周长:(8+5+18)×2
=(13+18)×2
=31×2
=62(dm)
面积:8×18+5×6
=144+30
=174(
)
