人教版数学四年级上册4单价、数量和总价课件(15张PPT)
文档属性
| 名称 | 人教版数学四年级上册4单价、数量和总价课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 08:17:56 | ||
图片预览




文档简介
(共15张PPT)
4
三位数乘两位数
第4课时 单价、数量和总价
新课导入—探究新知—课堂检测—课堂小结—课后作业
教学目标
教学重难点:
1.通过具体情境,知道单价、数量、总价的意义,初步理解三者之间的关系。
2.构建“单价×数量=总价、总价÷数量=单价、总价÷单价=数量”的数学模型。培养学生发现问题、分析问题和解决问题的能力。
3.体会数学与生活的密切联系,激发学生对数学的学习兴趣。
1.构建“单价×数量=总价、总价÷数量=单价、总价÷单价=数量”的数学模型。
2.运用单价、数量、总价三者之间的关系解决现实生活中的问题。
你们能解答这两个问题吗?
新课导入
(教材P52例4)
解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
80×3=_____(元)
240
(2)
鱼每千克10元,买
4千克要多少钱?
10×4=_____(元)
40
(教材P52例4)
解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
80×3=_____(元)
240
单价
数量
总价
(2)
鱼每千克10元,买
4千克要多少钱?
10×4=_____(元)
40
单价
数量
总价
这两道题,你们找到它们的共同点了吗?
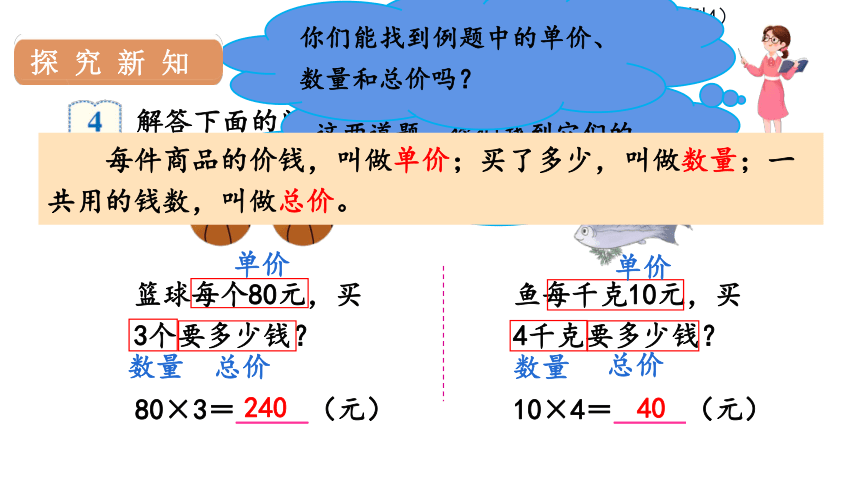
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用的钱数,叫做总价。
你们能找到例题中的单价、数量和总价吗?
探究新知
1. 举例说明什么是单价、数量和总价。
(教材P52做一做T1)
探究新知
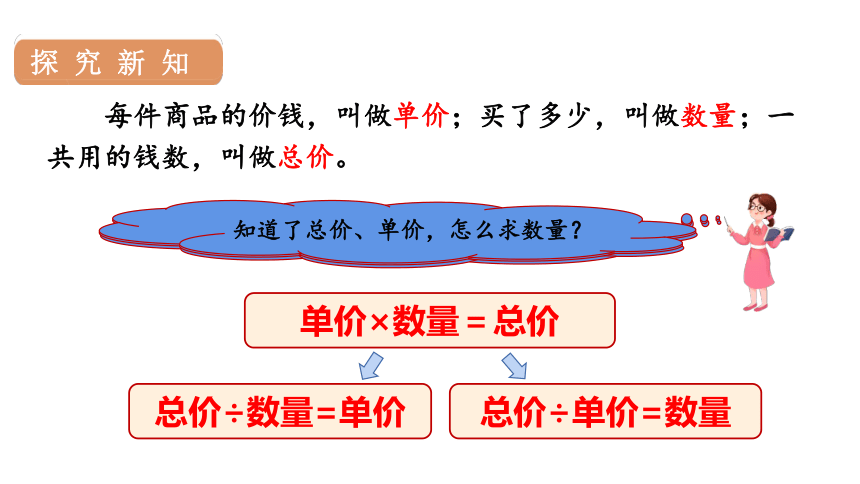
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用的钱数,叫做总价。
知道了单价、数量,怎么求总价?
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
知道了总价、数量,怎么求单价?
知道了总价、单价,怎么求数量?
探究新知
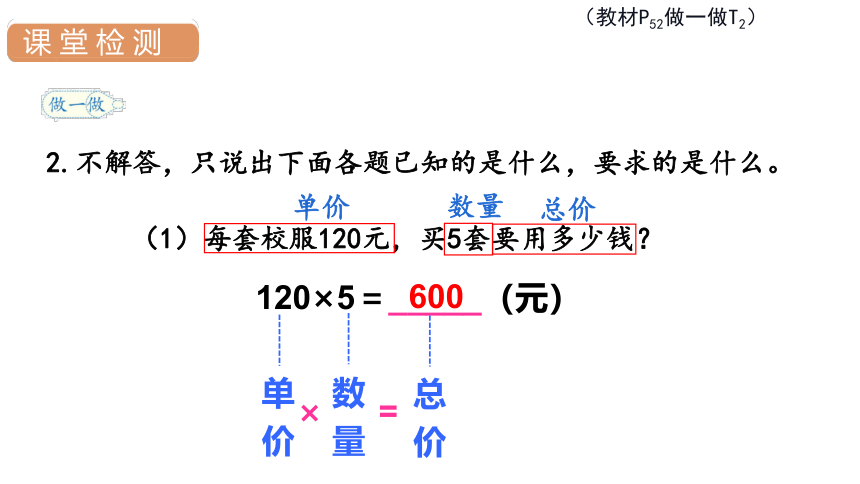
2.不解答,只说出下面各题已知的是什么,要求的是什么。
(1)每套校服120元,买5套要用多少钱?
120×5=_____(元)
600
单价
数量
总价
×
=
(教材P52做一做T2)
单价
数量
总价
课 堂 检 测
2.不解答,只说出下面各题已知的是什么,
要求的是什么。
(教材P52做一做T2)
(2)学校买了3台同样的复读机,花了420元,
每台复读机多少元?
420÷3=_____(元)
140
总价
数量
单价
÷
=
单价
数量
总价
课 堂 检 测
课 堂 检 测
(教材P55T8)
(1)18×3=54(元)
(2)18×2+21=57(元)
(3)18+21×2=60(元)
答:有三种买法。
课 堂 小 结
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用了多少钱,叫做总价。
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
课 后 作 业
1.根据单价、数量与总价的关系填写下面的表格。
1920
30
30
2.奥康影院1号影厅有120个座位。10月1日放映《我和我的祖国》,1号厅所有的票都卖完了,票价每张35元。这一场电影的收入是多少元?
120×35=4200(元)
答:这一场电影的收是4200元。
课 后 作 业
课 后 作 业
3.妈妈带1000元到商店买了4台同样的电扇,找回了40元。每台电扇多少钱?
答:每台电扇240元钱。
960÷4=240(元)
1000- 40=960(元)
课 后 作 业
4.根据12×25 =300编写一道关于单价、数量和总价的应用题。
某水果商店批发了25千克梨,每千克梨12元,批发这些梨一共花了多少钱?
(答案不唯一)
谢谢
4
三位数乘两位数
第4课时 单价、数量和总价
新课导入—探究新知—课堂检测—课堂小结—课后作业
教学目标
教学重难点:
1.通过具体情境,知道单价、数量、总价的意义,初步理解三者之间的关系。
2.构建“单价×数量=总价、总价÷数量=单价、总价÷单价=数量”的数学模型。培养学生发现问题、分析问题和解决问题的能力。
3.体会数学与生活的密切联系,激发学生对数学的学习兴趣。
1.构建“单价×数量=总价、总价÷数量=单价、总价÷单价=数量”的数学模型。
2.运用单价、数量、总价三者之间的关系解决现实生活中的问题。
你们能解答这两个问题吗?
新课导入
(教材P52例4)
解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
80×3=_____(元)
240
(2)
鱼每千克10元,买
4千克要多少钱?
10×4=_____(元)
40
(教材P52例4)
解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
80×3=_____(元)
240
单价
数量
总价
(2)
鱼每千克10元,买
4千克要多少钱?
10×4=_____(元)
40
单价
数量
总价
这两道题,你们找到它们的共同点了吗?
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用的钱数,叫做总价。
你们能找到例题中的单价、数量和总价吗?
探究新知
1. 举例说明什么是单价、数量和总价。
(教材P52做一做T1)
探究新知
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用的钱数,叫做总价。
知道了单价、数量,怎么求总价?
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
知道了总价、数量,怎么求单价?
知道了总价、单价,怎么求数量?
探究新知
2.不解答,只说出下面各题已知的是什么,要求的是什么。
(1)每套校服120元,买5套要用多少钱?
120×5=_____(元)
600
单价
数量
总价
×
=
(教材P52做一做T2)
单价
数量
总价
课 堂 检 测
2.不解答,只说出下面各题已知的是什么,
要求的是什么。
(教材P52做一做T2)
(2)学校买了3台同样的复读机,花了420元,
每台复读机多少元?
420÷3=_____(元)
140
总价
数量
单价
÷
=
单价
数量
总价
课 堂 检 测
课 堂 检 测
(教材P55T8)
(1)18×3=54(元)
(2)18×2+21=57(元)
(3)18+21×2=60(元)
答:有三种买法。
课 堂 小 结
每件商品的价钱,叫做单价;买了多少,叫做数量;一共用了多少钱,叫做总价。
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
课 后 作 业
1.根据单价、数量与总价的关系填写下面的表格。
1920
30
30
2.奥康影院1号影厅有120个座位。10月1日放映《我和我的祖国》,1号厅所有的票都卖完了,票价每张35元。这一场电影的收入是多少元?
120×35=4200(元)
答:这一场电影的收是4200元。
课 后 作 业
课 后 作 业
3.妈妈带1000元到商店买了4台同样的电扇,找回了40元。每台电扇多少钱?
答:每台电扇240元钱。
960÷4=240(元)
1000- 40=960(元)
课 后 作 业
4.根据12×25 =300编写一道关于单价、数量和总价的应用题。
某水果商店批发了25千克梨,每千克梨12元,批发这些梨一共花了多少钱?
(答案不唯一)
谢谢
