2021-2022北师大版七上第一章 丰富的图形世界常考必刷题(含解析)
文档属性
| 名称 | 2021-2022北师大版七上第一章 丰富的图形世界常考必刷题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 16:15:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2021-2022北师大版七上第一章丰富的图形世界常考必刷题
时间120分钟
满分120分
一.选择题(每小题3分,共36分)
1.(2020秋?白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
2.(2020秋?巧家县期末)如图,绕直线l旋转一周可得圆锥体的是( )
A.
B.
C.
D.
3.(2021春?绥棱县期末)制作一个底面直径为10cm,长4m的圆柱形排水管,至少要用( )平方米材料.
A.12560
B.2.826
C.125.6
D.1.256
4.(2021?百色)下列展开图中,不是正方体展开图的是( )
A.
B.
C.
D.
5.(2021?巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
6.(2021?深圳)如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟
B.百
C.走
D.年
7.(2020秋?九江期末)用一个平面去截一个几何体,下列几何体中截面可能是圆的是( )
A.正方体
B.长方体
C.球
D.六棱柱
8.(2021?曲江区校级模拟)用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A.
B.
C.
D.
9.(2021?沈阳)如图是由6个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A.
B.
C.
D.
10.(2021?朝阳)如图所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )
A.
B.
C.
D.
11.(2021?滨州)如图所示的几何体,是由几个相同的小正方体组合而成的,其俯视图为( )
A.
B.
C.
D.
12.(2021?湘潭)下列几何体中,三视图不含圆的是( )
A.
B.
C.
D.
二.填空题(每小题4分,共24分)
13.(2021春?宝山区期末)如果将两个棱长分别为3cm、5cm、7cm的相同的长方体拼成一个大长方体,那么它们的表面积(前后)最多减少
(cm)2.
14.(2021春?绥棱县期末)以一个边长为8厘米和5厘米的长方形其中一条边为轴旋转一周会得到一个圆柱体,这个圆柱的体积是
立方厘米.(结果保留π)
15.(2020秋?光明区期末)如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第
号小正方形.
16.(2020秋?皇姑区期末)如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数分别为
.
17.(2021?邗江区二模)如图是由6个大小相同的小正方体拼成的几何体,若去掉最左面的小正方体,则视图不发生改变的是
.(填主视图、左视图或俯视图)
18.(2019?禅城区一模)如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放
个小正方体.
三.解答题(共60分)
19.(8分)(2020秋?肇源县期末)有一个粮仓如图,如果每立方米粮食的质量为400千克,这个粮仓最多能装多少千克粮食?
20.(5分)(2014秋?清镇市校级期中)第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来.
21.(12分)(2020秋?解放区校级月考)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
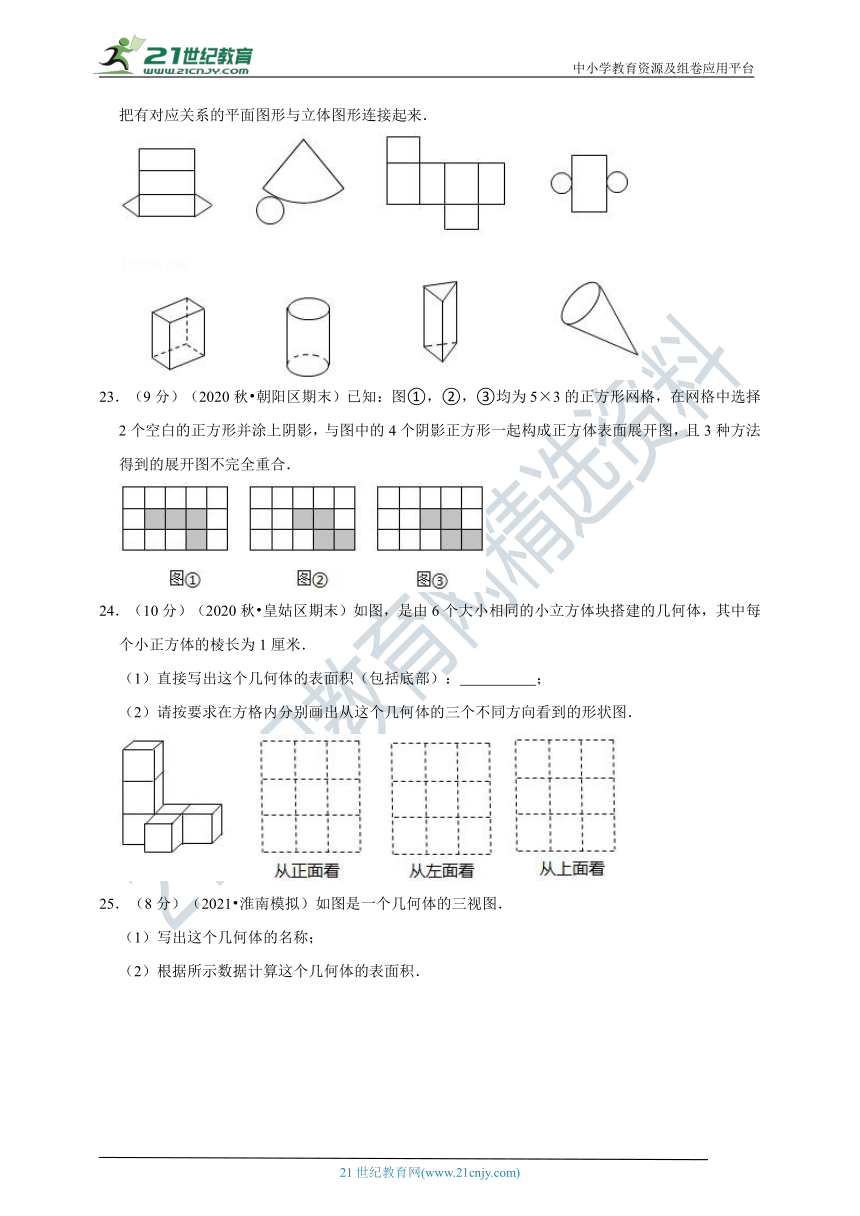
22.(8分)(2020秋?河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
23.(9分)(2020秋?朝阳区期末)已知:图①,②,③均为5×3的正方形网格,在网格中选择2个空白的正方形并涂上阴影,与图中的4个阴影正方形一起构成正方体表面展开图,且3种方法得到的展开图不完全重合.
24.(10分)(2020秋?皇姑区期末)如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部):
;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
25.(8分)(2021?淮南模拟)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积.
2021-2022北师大版七上第一章丰富的图形世界常考必刷题
参考答案与试题解析
一.选择题
1.(2020秋?白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
【分析】分别分析选项中各个图形有几个面然后确定正确答案即可.
【解答】解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
2.(2020秋?巧家县期末)如图,绕直线l旋转一周可得圆锥体的是( )
A.
B.
C.
D.
【分析】根据各种图形旋转所得到的几何体进行判断即可.
【解答】解:选项A中的图形绕直线l旋转一周,所得到的几何体是圆柱体,因此选项A不符合题意;
选项B中的图形绕直线l旋转一周,所得到的几何体是圆锥体,因此选项B符合题意;
选项C中的图形绕直线l旋转一周,所得到的几何体是球体,因此选项C不符合题意;
选项D中的图形绕直线l旋转一周,所得到的几何体是两个底面相同的圆锥体的组合体,因此选项D不符合题意;
故选:B.
3.(2021春?绥棱县期末)制作一个底面直径为10cm,长4m的圆柱形排水管,至少要用( )平方米材料.
A.12560
B.2.826
C.125.6
D.1.256
【分析】求所用材料的面积即为求该圆柱的侧面积,先统一单位再计算.
【解答】解:10cm=0.1m,
S侧面积=π×d×l
=3.14×0.1×4
=1.256(m2),
故选:D.
4.(2021?百色)下列展开图中,不是正方体展开图的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:选项A、B、C均能围成正方体;
选项D围成几何体时,有两个面重合,故不能围成正方体.
故选:D.
5.(2021?巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
【分析】利用立体图形及其表面展开图的特点解题.
【解答】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
6.(2021?深圳)如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟
B.百
C.走
D.年
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,和“建”字所在面相对的面上的字是“百”.
故选:B.
7.(2020秋?九江期末)用一个平面去截一个几何体,下列几何体中截面可能是圆的是( )
A.正方体
B.长方体
C.球
D.六棱柱
【分析】根据正方体、长方体、六棱柱和球的特点判断即可.
【解答】解:由题意可得,正方体、长方体、六棱柱的截面不可能为圆,而球的截面为圆,
故选:C.
8.(2021?曲江区校级模拟)用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A.
B.
C.
D.
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,截面也不可能有弧度,因此截面形状不可能为圆.
【解答】解:用一个平面无论如何去截,截面也不可能有弧度,因此截面形状不可能为圆.
故选:C.
9.(2021?沈阳)如图是由6个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A.
B.
C.
D.
【分析】利用主视图的定义进行判断即可,即从几何体的正面观察得出视图.
【解答】解:从几何体的正面看,底层是四个小正方形,上层的左端是一个小正方形.
故选:B.
10.(2021?朝阳)如图所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )
A.
B.
C.
D.
【分析】根据左视图是从左边看所得到的图形,可直接得到答案.
【解答】解:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:A.
11.(2021?滨州)如图所示的几何体,是由几个相同的小正方体组合而成的,其俯视图为( )
A.
B.
C.
D.
【分析】根据题目中的立体图形,可以直接作出它的俯视图,从而可以解答本题.
【解答】解:由图可得,
俯视图为:,
故选:B.
12.(2021?湘潭)下列几何体中,三视图不含圆的是( )
A.
B.
C.
D.
【分析】分别找出四个立体图形的三视图即可解答.
【解答】解:A、圆柱的俯视图是圆,故不符合题意;
B、球的三视图都是圆,故不符合题意;
C、正方体的三视图都是正方形,故符合题意;
D、圆锥的俯视图是圆,故不符合答题,
故选:C.
二.填空题
13.(2021春?宝山区期末)如果将两个棱长分别为3cm、5cm、7cm的相同的长方体拼成一个大长方体,那么它们的表面积(前后)最多减少
70 (cm)2.
【分析】将两个长方体拼在一起时,接触面积越大减小的面积越大,求两个最大的那个面的面积即可.
【解答】解:将两个长方体拼在一起时,接触面积越大减小的面积越大,
∴将长是7cm,宽是5cm的两个面拼在一起时减少的面积最多,
即7×5×2=70(cm2),
故答案为:70.
14.(2021春?绥棱县期末)以一个边长为8厘米和5厘米的长方形其中一条边为轴旋转一周会得到一个圆柱体,这个圆柱的体积是
200π或320π 立方厘米.(结果保留π)
【分析】圆柱的体积公式是:V=sh=πr2h,分别计算以8厘米和5厘米长的边为轴旋转得到的圆柱体积.
【解答】解:以8厘米长的边为轴旋转得到的圆柱体积=π×52×8=200π(立方厘米),
以5厘米长的边为轴旋转得到的圆柱体积=π×82×5=320π(立方厘米),
∴这个圆柱的体积是200π或320π立方厘米.
故答案为:200π或320π.
15.(2020秋?光明区期末)如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第 ①或② 号小正方形.
【分析】根据正方体的11种展开图的模型即可求解.
【解答】解:把图中的①或②减去,剩下的图形即为正方体的11种展开图中的模型,
故答案为:①或②.
16.(2020秋?皇姑区期末)如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数分别为 7,12 .
【分析】如图正方体切一个顶点多一个面,少三条棱,又多三条棱,依此即可求解.
得到面增加一个,棱增加3.
【解答】解:如图,一个正方体截去一个角后,剩下的几何体面的个数是6+1=7,棱的条数是12﹣3+3=12.
故选:7,12.
17.(2021?邗江区二模)如图是由6个大小相同的小正方体拼成的几何体,若去掉最左面的小正方体,则视图不发生改变的是
左视图 .(填主视图、左视图或俯视图)
【分析】根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.
【解答】解:若去掉最左面的小正方体,其左视图不变,即左视图依然还是三层,底层两个正方形,第二层有一个,顶层有一个正方形.
故答案为:左视图.
18.(2019?禅城区一模)如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放 1 个小正方体.
【分析】根据主视图是从正面看得到图形是主视图,从上面看得到的图形是俯视图,从左面看得到的图形是左视图,可得答案.
【解答】解:主视图是第一层三个小正方形,第二层是左边一个小正方形,中间一个小正方形,第三层是左边一个小正方形,
俯视图是第一层三个小正方形,第二层三个小正方形,
左视图是第一层两个小正方形,第二层两个小正方形,第三层左边一个小正方形,
不改变三视图,中间第二层加一个,
故答案为:1.
三.解答题
19.(2020秋?肇源县期末)有一个粮仓如图,如果每立方米粮食的质量为400千克,这个粮仓最多能装多少千克粮食?
【分析】先求出粮仓的体积,再计算粮食的质量.
【解答】解:粮仓的体积为:×3.14×(2÷2)2×0.6+3.14×(2÷2)2×1.5
=3.14×0.2+3.14×1.5
=0.628+4.71
=5.338(立方米),
5.338×400=2135.2(千克),
答:这个粮仓最多能装2135.2千克粮食.
20.(2014秋?清镇市校级期中)第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来.
【分析】根据面动成体:梯形绕底边旋转得中间圆柱、上下圆锥,半圆绕直径旋转得球,矩形绕边旋转得圆柱,直角三角形绕直角边旋转得圆锥,可得答案.
【解答】解:第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来为:
.
21.(2020秋?解放区校级月考)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
【分析】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,可得答案.
【解答】解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π?()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
22.(2020秋?河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【分析】根据常见几何体展开图的形状特征,或折叠成几何体的形状得出判断即可.
【解答】解:由简单几何体的展开与折叠可得,
23.(2020秋?朝阳区期末)已知:图①,②,③均为5×3的正方形网格,在网格中选择2个空白的正方形并涂上阴影,与图中的4个阴影正方形一起构成正方体表面展开图,且3种方法得到的展开图不完全重合.
【分析】依据正方体的展开图的结构特征进行判断,即可得出结论.
【解答】解:如图所示:(答案不唯一)
24.(2020秋?皇姑区期末)如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): 26cm2 ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
【分析】(1)三视图面积和的2倍即可;
(2)利用三视图的画法画出图形即可.
【解答】解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
25.(2021?淮南模拟)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积.
【分析】根据三视图得到几何体为圆锥,圆锥的母线长为6,圆锥底面圆的半径为2,然后计算侧面积和底面积的和即可.
【解答】解:(1)由三视图得几何体为圆锥,
(2)圆锥的表面积=π?22+?2π?6?2=16π.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2021-2022北师大版七上第一章丰富的图形世界常考必刷题
时间120分钟
满分120分
一.选择题(每小题3分,共36分)
1.(2020秋?白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
2.(2020秋?巧家县期末)如图,绕直线l旋转一周可得圆锥体的是( )
A.
B.
C.
D.
3.(2021春?绥棱县期末)制作一个底面直径为10cm,长4m的圆柱形排水管,至少要用( )平方米材料.
A.12560
B.2.826
C.125.6
D.1.256
4.(2021?百色)下列展开图中,不是正方体展开图的是( )
A.
B.
C.
D.
5.(2021?巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
6.(2021?深圳)如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟
B.百
C.走
D.年
7.(2020秋?九江期末)用一个平面去截一个几何体,下列几何体中截面可能是圆的是( )
A.正方体
B.长方体
C.球
D.六棱柱
8.(2021?曲江区校级模拟)用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A.
B.
C.
D.
9.(2021?沈阳)如图是由6个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A.
B.
C.
D.
10.(2021?朝阳)如图所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )
A.
B.
C.
D.
11.(2021?滨州)如图所示的几何体,是由几个相同的小正方体组合而成的,其俯视图为( )
A.
B.
C.
D.
12.(2021?湘潭)下列几何体中,三视图不含圆的是( )
A.
B.
C.
D.
二.填空题(每小题4分,共24分)
13.(2021春?宝山区期末)如果将两个棱长分别为3cm、5cm、7cm的相同的长方体拼成一个大长方体,那么它们的表面积(前后)最多减少
(cm)2.
14.(2021春?绥棱县期末)以一个边长为8厘米和5厘米的长方形其中一条边为轴旋转一周会得到一个圆柱体,这个圆柱的体积是
立方厘米.(结果保留π)
15.(2020秋?光明区期末)如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第
号小正方形.
16.(2020秋?皇姑区期末)如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数分别为
.
17.(2021?邗江区二模)如图是由6个大小相同的小正方体拼成的几何体,若去掉最左面的小正方体,则视图不发生改变的是
.(填主视图、左视图或俯视图)
18.(2019?禅城区一模)如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放
个小正方体.
三.解答题(共60分)
19.(8分)(2020秋?肇源县期末)有一个粮仓如图,如果每立方米粮食的质量为400千克,这个粮仓最多能装多少千克粮食?
20.(5分)(2014秋?清镇市校级期中)第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来.
21.(12分)(2020秋?解放区校级月考)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
22.(8分)(2020秋?河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
23.(9分)(2020秋?朝阳区期末)已知:图①,②,③均为5×3的正方形网格,在网格中选择2个空白的正方形并涂上阴影,与图中的4个阴影正方形一起构成正方体表面展开图,且3种方法得到的展开图不完全重合.
24.(10分)(2020秋?皇姑区期末)如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部):
;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
25.(8分)(2021?淮南模拟)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积.
2021-2022北师大版七上第一章丰富的图形世界常考必刷题
参考答案与试题解析
一.选择题
1.(2020秋?白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
【分析】分别分析选项中各个图形有几个面然后确定正确答案即可.
【解答】解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
2.(2020秋?巧家县期末)如图,绕直线l旋转一周可得圆锥体的是( )
A.
B.
C.
D.
【分析】根据各种图形旋转所得到的几何体进行判断即可.
【解答】解:选项A中的图形绕直线l旋转一周,所得到的几何体是圆柱体,因此选项A不符合题意;
选项B中的图形绕直线l旋转一周,所得到的几何体是圆锥体,因此选项B符合题意;
选项C中的图形绕直线l旋转一周,所得到的几何体是球体,因此选项C不符合题意;
选项D中的图形绕直线l旋转一周,所得到的几何体是两个底面相同的圆锥体的组合体,因此选项D不符合题意;
故选:B.
3.(2021春?绥棱县期末)制作一个底面直径为10cm,长4m的圆柱形排水管,至少要用( )平方米材料.
A.12560
B.2.826
C.125.6
D.1.256
【分析】求所用材料的面积即为求该圆柱的侧面积,先统一单位再计算.
【解答】解:10cm=0.1m,
S侧面积=π×d×l
=3.14×0.1×4
=1.256(m2),
故选:D.
4.(2021?百色)下列展开图中,不是正方体展开图的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:选项A、B、C均能围成正方体;
选项D围成几何体时,有两个面重合,故不能围成正方体.
故选:D.
5.(2021?巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
【分析】利用立体图形及其表面展开图的特点解题.
【解答】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
6.(2021?深圳)如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟
B.百
C.走
D.年
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,和“建”字所在面相对的面上的字是“百”.
故选:B.
7.(2020秋?九江期末)用一个平面去截一个几何体,下列几何体中截面可能是圆的是( )
A.正方体
B.长方体
C.球
D.六棱柱
【分析】根据正方体、长方体、六棱柱和球的特点判断即可.
【解答】解:由题意可得,正方体、长方体、六棱柱的截面不可能为圆,而球的截面为圆,
故选:C.
8.(2021?曲江区校级模拟)用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A.
B.
C.
D.
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,截面也不可能有弧度,因此截面形状不可能为圆.
【解答】解:用一个平面无论如何去截,截面也不可能有弧度,因此截面形状不可能为圆.
故选:C.
9.(2021?沈阳)如图是由6个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A.
B.
C.
D.
【分析】利用主视图的定义进行判断即可,即从几何体的正面观察得出视图.
【解答】解:从几何体的正面看,底层是四个小正方形,上层的左端是一个小正方形.
故选:B.
10.(2021?朝阳)如图所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )
A.
B.
C.
D.
【分析】根据左视图是从左边看所得到的图形,可直接得到答案.
【解答】解:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:A.
11.(2021?滨州)如图所示的几何体,是由几个相同的小正方体组合而成的,其俯视图为( )
A.
B.
C.
D.
【分析】根据题目中的立体图形,可以直接作出它的俯视图,从而可以解答本题.
【解答】解:由图可得,
俯视图为:,
故选:B.
12.(2021?湘潭)下列几何体中,三视图不含圆的是( )
A.
B.
C.
D.
【分析】分别找出四个立体图形的三视图即可解答.
【解答】解:A、圆柱的俯视图是圆,故不符合题意;
B、球的三视图都是圆,故不符合题意;
C、正方体的三视图都是正方形,故符合题意;
D、圆锥的俯视图是圆,故不符合答题,
故选:C.
二.填空题
13.(2021春?宝山区期末)如果将两个棱长分别为3cm、5cm、7cm的相同的长方体拼成一个大长方体,那么它们的表面积(前后)最多减少
70 (cm)2.
【分析】将两个长方体拼在一起时,接触面积越大减小的面积越大,求两个最大的那个面的面积即可.
【解答】解:将两个长方体拼在一起时,接触面积越大减小的面积越大,
∴将长是7cm,宽是5cm的两个面拼在一起时减少的面积最多,
即7×5×2=70(cm2),
故答案为:70.
14.(2021春?绥棱县期末)以一个边长为8厘米和5厘米的长方形其中一条边为轴旋转一周会得到一个圆柱体,这个圆柱的体积是
200π或320π 立方厘米.(结果保留π)
【分析】圆柱的体积公式是:V=sh=πr2h,分别计算以8厘米和5厘米长的边为轴旋转得到的圆柱体积.
【解答】解:以8厘米长的边为轴旋转得到的圆柱体积=π×52×8=200π(立方厘米),
以5厘米长的边为轴旋转得到的圆柱体积=π×82×5=320π(立方厘米),
∴这个圆柱的体积是200π或320π立方厘米.
故答案为:200π或320π.
15.(2020秋?光明区期末)如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第 ①或② 号小正方形.
【分析】根据正方体的11种展开图的模型即可求解.
【解答】解:把图中的①或②减去,剩下的图形即为正方体的11种展开图中的模型,
故答案为:①或②.
16.(2020秋?皇姑区期末)如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数分别为 7,12 .
【分析】如图正方体切一个顶点多一个面,少三条棱,又多三条棱,依此即可求解.
得到面增加一个,棱增加3.
【解答】解:如图,一个正方体截去一个角后,剩下的几何体面的个数是6+1=7,棱的条数是12﹣3+3=12.
故选:7,12.
17.(2021?邗江区二模)如图是由6个大小相同的小正方体拼成的几何体,若去掉最左面的小正方体,则视图不发生改变的是
左视图 .(填主视图、左视图或俯视图)
【分析】根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.
【解答】解:若去掉最左面的小正方体,其左视图不变,即左视图依然还是三层,底层两个正方形,第二层有一个,顶层有一个正方形.
故答案为:左视图.
18.(2019?禅城区一模)如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放 1 个小正方体.
【分析】根据主视图是从正面看得到图形是主视图,从上面看得到的图形是俯视图,从左面看得到的图形是左视图,可得答案.
【解答】解:主视图是第一层三个小正方形,第二层是左边一个小正方形,中间一个小正方形,第三层是左边一个小正方形,
俯视图是第一层三个小正方形,第二层三个小正方形,
左视图是第一层两个小正方形,第二层两个小正方形,第三层左边一个小正方形,
不改变三视图,中间第二层加一个,
故答案为:1.
三.解答题
19.(2020秋?肇源县期末)有一个粮仓如图,如果每立方米粮食的质量为400千克,这个粮仓最多能装多少千克粮食?
【分析】先求出粮仓的体积,再计算粮食的质量.
【解答】解:粮仓的体积为:×3.14×(2÷2)2×0.6+3.14×(2÷2)2×1.5
=3.14×0.2+3.14×1.5
=0.628+4.71
=5.338(立方米),
5.338×400=2135.2(千克),
答:这个粮仓最多能装2135.2千克粮食.
20.(2014秋?清镇市校级期中)第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来.
【分析】根据面动成体:梯形绕底边旋转得中间圆柱、上下圆锥,半圆绕直径旋转得球,矩形绕边旋转得圆柱,直角三角形绕直角边旋转得圆锥,可得答案.
【解答】解:第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来为:
.
21.(2020秋?解放区校级月考)小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
【分析】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,可得答案.
【解答】解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π?()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
22.(2020秋?河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【分析】根据常见几何体展开图的形状特征,或折叠成几何体的形状得出判断即可.
【解答】解:由简单几何体的展开与折叠可得,
23.(2020秋?朝阳区期末)已知:图①,②,③均为5×3的正方形网格,在网格中选择2个空白的正方形并涂上阴影,与图中的4个阴影正方形一起构成正方体表面展开图,且3种方法得到的展开图不完全重合.
【分析】依据正方体的展开图的结构特征进行判断,即可得出结论.
【解答】解:如图所示:(答案不唯一)
24.(2020秋?皇姑区期末)如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): 26cm2 ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
【分析】(1)三视图面积和的2倍即可;
(2)利用三视图的画法画出图形即可.
【解答】解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
25.(2021?淮南模拟)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积.
【分析】根据三视图得到几何体为圆锥,圆锥的母线长为6,圆锥底面圆的半径为2,然后计算侧面积和底面积的和即可.
【解答】解:(1)由三视图得几何体为圆锥,
(2)圆锥的表面积=π?22+?2π?6?2=16π.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
