苏科版七年级数学上册第3章 代数式 复习 课件(共29张PPT)
文档属性
| 名称 | 苏科版七年级数学上册第3章 代数式 复习 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 541.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 08:48:54 | ||
图片预览







文档简介
(共29张PPT)
第3章
代数式
复习课件
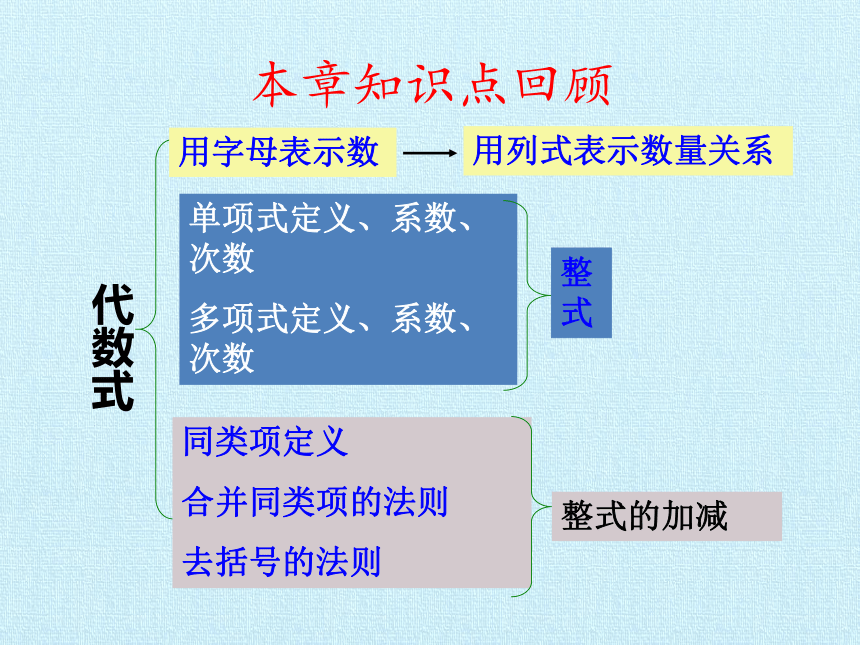
本章知识点回顾
用字母表示数
用列式表示数量关系
单项式定义、系数、次数
多项式定义、系数、次数
整式
同类项定义
合并同类项的法则
去括号的法则
整式的加减
代数式
列代数式
应该注意四点:
(1)代数式中出现乘号,通常写作“.”或者省略不写。
(2)数字与字母相乘时,数字写在字母前面。
(3)除法运算写成分数形式。
(4)当表示和或差而后面有单位时,代数式应加括号。
用代数式表示乙数:
(1)乙数比x大5;
(2)乙数比x的2倍小3;
(3)乙数比x的倒数小7;
(4)乙数比x大16%。?
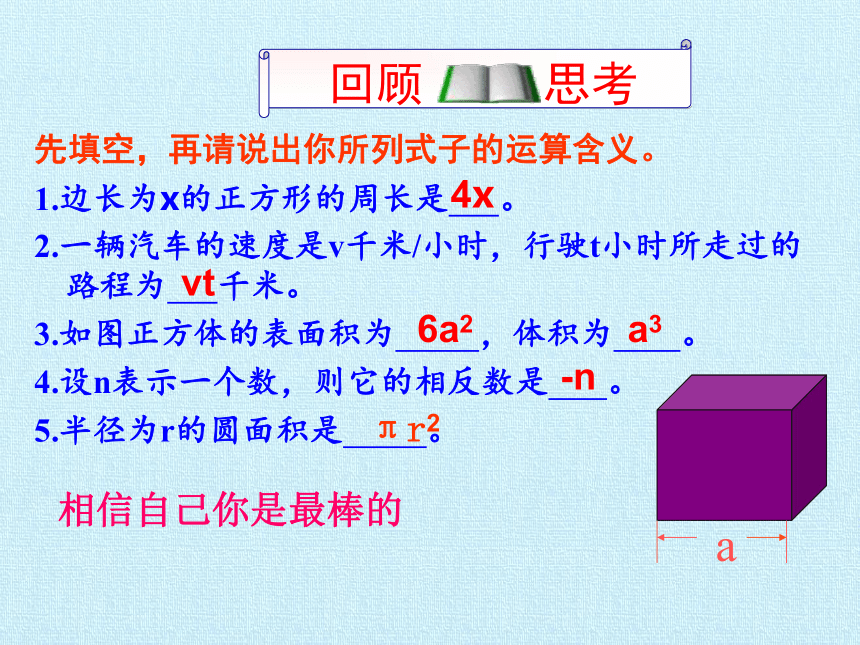
先填空,再请说出你所列式子的运算含义。
1.边长为x的正方形的周长是
。
2.一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为
千米。
3.如图正方体的表面积为
,体积为
。
4.设n表示一个数,则它的相反数是
。
5.半径为r的圆面积是
。
4x
vt
a3
6a2
-n
πr2
a
相信自己你是最棒的
回顾
思考
1、温度由toc下降5oc后是
oc。
2、买一个篮球需要x元,买一个排球需
要y元买一个足球需要z元,买3个篮球、
5个排球、2个足球共需要
元。
3、如图三角尺的面积为
;
4、如图是一所住宅区的建筑平面图,这所
住宅的建筑面积是
㎡。
3x+5y+2z
x2+2x+18
t-5
(1)单项式是由数与字母的乘积组成的代数式;
单独的一个数或字母也是单项式;
单项式的数字因数叫做单项式的系数;
单项式中所有字母的指数的和叫做单项式的次数,而且次数只与字母有关。
关于整式的概念
关于整式的概念
(2)多项式是建立在单项式概念基础上,几个单项式的和就是多项式;
每个单项式是该多项式的一个项;每项包括它前面的符号,这点一定要注意。
组成多项式的每个单项式的次数是该多项式各项的次数;“几次项”中“次”就是指这个次数;
多项式的次数,是指示最高次项发次数。
(3)单项式和多项式是统称为整式。
指出下列代数式中哪些是单项式?哪些是多项式?哪些是整式?
[例1]
评析:本题需应用单项式、多项式、整式的意义来解答。单项式只含有“乘积”运算;多项式必须含有加法或减法运算。不论单项式还是多项式,分母中都不能含有字母。
解:
单项式有:
多项式有:
整式有:
火眼金睛
下面各题的判断是否正确。
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是
。(
)
×
×
×
×
×
√
1.单项式m2n2的系数是_____,次数是_____,m2n2是____次单项式。
2.多项式x+y-z是单项式
的和,它是___次___项式。
3.多项式3m3-2m-5+m2的常数项是____,
一次项是_____,二次项的系数是_____。
1
4
4
x
、y
、-z
1
3
-5
-2m
1
成长的足迹
4.如果-5xym-1为4次单项式,则m=____。
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a=____,b=____。
1/2
2
成长的足迹
6.多项式-3a2b3+5a2b2-4ab-2共有几项,多项式的次数是多少?第三项是什么,它的系数和次数分别是多少?
根据加法的交换律和结合律,可以把一个多项式的各项重新排列,移动多项式的项时,需连同项的符号一起移动,这样的移动并没有改变项的符号和多项式的值。
把一个多项式按某个字母的指数从大到小的顺序排列起来叫做把该多项式按这个字母的降幂排列;
把一个多项式按某个字母的指数从小到大的顺序排列起来叫做把该多项式按这个字母的升幂排列。
排列时,一定要看清楚是按哪个字母,进行什么样的排列(升幂或降幂)。
[例2]
评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。
(1)按x的升幂排列;(2)按y的降幂排列。
解:
(1)按x的升幂排列:
(2)按y的降幂排列:
关于同类项和合并同类项
1、对于同类项应从概念出发,掌握判断标准:
(1)字母相同;
(2)相同字母的指数相同;
(3)与系数无关;
(4)与字母的顺序无关。
两相同
两无关
关于同类项和合并同类项
2、合并同类项是整式加减的基础。法则:合并同类项,只把系数相加减,字母及字母的指数不变。
注意以下几点:(前提:正确判断同类项)
(1)常数项是同类项,所以几个常数项可以合并;
(2)两个同类项系数互为相反数,则这两项的和等于0;
(3)同类项中的“合并”是指同类项系数求和,把所得到结果作为新的项的系数,字母与字母的指数不变。
(4)只有同类项才能合并,不是同类项就不能合并。
练一练:
1.说出下列各组中的两个单项式是不是同类项?为什么?
(1)x2y与-3yx2;
(2)a2b2与-ab2;
(3)-3与6;
(4)2a与ab
2.指出4x2-8x+5-3x2-6x-2中的同类项
不是
是
不是
是
多项式中的项:
4x2,-8x,+5,-3x2,-6x,-2
同类项:
4x2与-3x2
-8x与-6x
+5与-2
3.化简:(1)-xy2–xy2
(2)–3x2y-3xy2+2x2y-2xy2
1.已知:
与
是同类项,求m、n的值。
2
_
3
x3my3
-
1
_
4
x6yn+1
2.已知:
与
能合并。则
m=
,n=_____。
3.关于a,b的多项式
不ab含项。则m=_____。
知识回顾
4.如果2a2bn+1与-4amb3是同类项,则m=___,n=__;
5.若5xy2+axy2=-2xy2,则a=____;
6.在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是___。
2
3
3
2
2
-7
6xy
下列各题合并同类项的结果对不对?若不对,
请改正。
(1)
(2)
(3)
(4)
练习(合并下列各式的同类项)
(1)-xy2–
xy2
(2)–3x2y-3xy2+2x2y-2xy2
(3)4a2+3b2+2ab-4a2-4b2
(4)m-n2+m-n2
×
√
×
×
[例1]
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;
解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
思考:计算(1)-a2-a2-a2;(2)a3+a2b+ab2-a2b-ab2-b2
1、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号(
);
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号(
)。
遇到括号前面是“-”时,容易发生漏掉括号内一部分项的变号,所以,要注意“各项”都要变号。不是只变第一项的符号。
去括号的顺口溜:去括号,看符号;
是正号,不变号;
是负号,全变号。
关于去括号
相同
相反
练一练,老师相信你们的实力!
判断下列计算是否正确:
不正确
不正确
正确
不正确
(5)-a-{-2a-[-3a-(a-1)-6]-5}
化简下列各式:
利用去括号的规律进行整式的化简:
1、整式的加减是本章节的重点,是全章知识的综合与运用掌握了整式的加减就掌握了本章的知识。
整式加减的一般步骤是:
(1)如果有括号,那么要先去括号;
(2)如果有同类项,再合并同类项;
关于整式的加减
[例1]
求减去-x3+2x2-3x-1的差为-2x2+3x-2的多项式
评析:把一个代数式看成整体,添上括号。利用已知减数和差,求被减数应该用加法运算。
解:(-x3+2x2-3x-1)+(-2x2+3x-2)
=-x3+2x2-3x-1-2x2+3x-2=-x3-3
答:所求多项式为-x3-3。
已知a2+ab=-3,ab+b2=7,试求a2+2ab+b2;a2-b2的值。
[例2]
解:a2+2ab+b2=(a2+ab)+(ab+b2)=-3+7=4
a2-b2=(a2+ab)-(ab+b2)=-3-7=-10
评析:这是利用“整体代入”思想求值的一个典型题目,关键是利用“拆项”后添加括号重新组合,巧妙求解。
乙旅行团成人数为:
门票费用为
:
元,
儿童的人数为:
门票费用为:
元.
总和是
元
例题:一公园的成票价是15元,儿童买半票,甲旅行团有x(名)成年人和y(名)儿童;乙旅行团的成人数是甲旅行团的2倍,儿童数比甲旅行团的2倍少8人,这两个旅行团的门票费用总和各是多少?
解析:甲旅行团成人的门票费用为
元,
儿童的门票费用为:
元。
总和是
元
30x
2x
(2y-8)
7.5(2y-8)
[30x+7.5(2y-8)]
即(30x+15y-60)元
15X
7.5y
(15x+7.5y)
[练习]
2.已知a2-ab=2,4ab-3b2=-3,试求a2-13ab+9b2-5的值。
1.化简求值:3x2-[7x-(4x-3)-2x3],其中x=-0.5
3.某人做了一道题:
“一个多项式减去3x2-5x+1…”,他误将减去3x2-5x+1写为加上3x2-5x+1,得出的结果是5x2+3x-7。求出这道题的正确结果。
提示:a2-13ab+9b2-5=(a2-ab)-3(4ab-3b2)-5
答案:-1
提示:先设被减数为A,可由已知求出多项式A,再计算A-(3x2-5x+1)
谢
谢
第3章
代数式
复习课件
本章知识点回顾
用字母表示数
用列式表示数量关系
单项式定义、系数、次数
多项式定义、系数、次数
整式
同类项定义
合并同类项的法则
去括号的法则
整式的加减
代数式
列代数式
应该注意四点:
(1)代数式中出现乘号,通常写作“.”或者省略不写。
(2)数字与字母相乘时,数字写在字母前面。
(3)除法运算写成分数形式。
(4)当表示和或差而后面有单位时,代数式应加括号。
用代数式表示乙数:
(1)乙数比x大5;
(2)乙数比x的2倍小3;
(3)乙数比x的倒数小7;
(4)乙数比x大16%。?
先填空,再请说出你所列式子的运算含义。
1.边长为x的正方形的周长是
。
2.一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为
千米。
3.如图正方体的表面积为
,体积为
。
4.设n表示一个数,则它的相反数是
。
5.半径为r的圆面积是
。
4x
vt
a3
6a2
-n
πr2
a
相信自己你是最棒的
回顾
思考
1、温度由toc下降5oc后是
oc。
2、买一个篮球需要x元,买一个排球需
要y元买一个足球需要z元,买3个篮球、
5个排球、2个足球共需要
元。
3、如图三角尺的面积为
;
4、如图是一所住宅区的建筑平面图,这所
住宅的建筑面积是
㎡。
3x+5y+2z
x2+2x+18
t-5
(1)单项式是由数与字母的乘积组成的代数式;
单独的一个数或字母也是单项式;
单项式的数字因数叫做单项式的系数;
单项式中所有字母的指数的和叫做单项式的次数,而且次数只与字母有关。
关于整式的概念
关于整式的概念
(2)多项式是建立在单项式概念基础上,几个单项式的和就是多项式;
每个单项式是该多项式的一个项;每项包括它前面的符号,这点一定要注意。
组成多项式的每个单项式的次数是该多项式各项的次数;“几次项”中“次”就是指这个次数;
多项式的次数,是指示最高次项发次数。
(3)单项式和多项式是统称为整式。
指出下列代数式中哪些是单项式?哪些是多项式?哪些是整式?
[例1]
评析:本题需应用单项式、多项式、整式的意义来解答。单项式只含有“乘积”运算;多项式必须含有加法或减法运算。不论单项式还是多项式,分母中都不能含有字母。
解:
单项式有:
多项式有:
整式有:
火眼金睛
下面各题的判断是否正确。
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是
。(
)
×
×
×
×
×
√
1.单项式m2n2的系数是_____,次数是_____,m2n2是____次单项式。
2.多项式x+y-z是单项式
的和,它是___次___项式。
3.多项式3m3-2m-5+m2的常数项是____,
一次项是_____,二次项的系数是_____。
1
4
4
x
、y
、-z
1
3
-5
-2m
1
成长的足迹
4.如果-5xym-1为4次单项式,则m=____。
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a=____,b=____。
1/2
2
成长的足迹
6.多项式-3a2b3+5a2b2-4ab-2共有几项,多项式的次数是多少?第三项是什么,它的系数和次数分别是多少?
根据加法的交换律和结合律,可以把一个多项式的各项重新排列,移动多项式的项时,需连同项的符号一起移动,这样的移动并没有改变项的符号和多项式的值。
把一个多项式按某个字母的指数从大到小的顺序排列起来叫做把该多项式按这个字母的降幂排列;
把一个多项式按某个字母的指数从小到大的顺序排列起来叫做把该多项式按这个字母的升幂排列。
排列时,一定要看清楚是按哪个字母,进行什么样的排列(升幂或降幂)。
[例2]
评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。
(1)按x的升幂排列;(2)按y的降幂排列。
解:
(1)按x的升幂排列:
(2)按y的降幂排列:
关于同类项和合并同类项
1、对于同类项应从概念出发,掌握判断标准:
(1)字母相同;
(2)相同字母的指数相同;
(3)与系数无关;
(4)与字母的顺序无关。
两相同
两无关
关于同类项和合并同类项
2、合并同类项是整式加减的基础。法则:合并同类项,只把系数相加减,字母及字母的指数不变。
注意以下几点:(前提:正确判断同类项)
(1)常数项是同类项,所以几个常数项可以合并;
(2)两个同类项系数互为相反数,则这两项的和等于0;
(3)同类项中的“合并”是指同类项系数求和,把所得到结果作为新的项的系数,字母与字母的指数不变。
(4)只有同类项才能合并,不是同类项就不能合并。
练一练:
1.说出下列各组中的两个单项式是不是同类项?为什么?
(1)x2y与-3yx2;
(2)a2b2与-ab2;
(3)-3与6;
(4)2a与ab
2.指出4x2-8x+5-3x2-6x-2中的同类项
不是
是
不是
是
多项式中的项:
4x2,-8x,+5,-3x2,-6x,-2
同类项:
4x2与-3x2
-8x与-6x
+5与-2
3.化简:(1)-xy2–xy2
(2)–3x2y-3xy2+2x2y-2xy2
1.已知:
与
是同类项,求m、n的值。
2
_
3
x3my3
-
1
_
4
x6yn+1
2.已知:
与
能合并。则
m=
,n=_____。
3.关于a,b的多项式
不ab含项。则m=_____。
知识回顾
4.如果2a2bn+1与-4amb3是同类项,则m=___,n=__;
5.若5xy2+axy2=-2xy2,则a=____;
6.在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是___。
2
3
3
2
2
-7
6xy
下列各题合并同类项的结果对不对?若不对,
请改正。
(1)
(2)
(3)
(4)
练习(合并下列各式的同类项)
(1)-xy2–
xy2
(2)–3x2y-3xy2+2x2y-2xy2
(3)4a2+3b2+2ab-4a2-4b2
(4)m-n2+m-n2
×
√
×
×
[例1]
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;
解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
思考:计算(1)-a2-a2-a2;(2)a3+a2b+ab2-a2b-ab2-b2
1、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号(
);
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号(
)。
遇到括号前面是“-”时,容易发生漏掉括号内一部分项的变号,所以,要注意“各项”都要变号。不是只变第一项的符号。
去括号的顺口溜:去括号,看符号;
是正号,不变号;
是负号,全变号。
关于去括号
相同
相反
练一练,老师相信你们的实力!
判断下列计算是否正确:
不正确
不正确
正确
不正确
(5)-a-{-2a-[-3a-(a-1)-6]-5}
化简下列各式:
利用去括号的规律进行整式的化简:
1、整式的加减是本章节的重点,是全章知识的综合与运用掌握了整式的加减就掌握了本章的知识。
整式加减的一般步骤是:
(1)如果有括号,那么要先去括号;
(2)如果有同类项,再合并同类项;
关于整式的加减
[例1]
求减去-x3+2x2-3x-1的差为-2x2+3x-2的多项式
评析:把一个代数式看成整体,添上括号。利用已知减数和差,求被减数应该用加法运算。
解:(-x3+2x2-3x-1)+(-2x2+3x-2)
=-x3+2x2-3x-1-2x2+3x-2=-x3-3
答:所求多项式为-x3-3。
已知a2+ab=-3,ab+b2=7,试求a2+2ab+b2;a2-b2的值。
[例2]
解:a2+2ab+b2=(a2+ab)+(ab+b2)=-3+7=4
a2-b2=(a2+ab)-(ab+b2)=-3-7=-10
评析:这是利用“整体代入”思想求值的一个典型题目,关键是利用“拆项”后添加括号重新组合,巧妙求解。
乙旅行团成人数为:
门票费用为
:
元,
儿童的人数为:
门票费用为:
元.
总和是
元
例题:一公园的成票价是15元,儿童买半票,甲旅行团有x(名)成年人和y(名)儿童;乙旅行团的成人数是甲旅行团的2倍,儿童数比甲旅行团的2倍少8人,这两个旅行团的门票费用总和各是多少?
解析:甲旅行团成人的门票费用为
元,
儿童的门票费用为:
元。
总和是
元
30x
2x
(2y-8)
7.5(2y-8)
[30x+7.5(2y-8)]
即(30x+15y-60)元
15X
7.5y
(15x+7.5y)
[练习]
2.已知a2-ab=2,4ab-3b2=-3,试求a2-13ab+9b2-5的值。
1.化简求值:3x2-[7x-(4x-3)-2x3],其中x=-0.5
3.某人做了一道题:
“一个多项式减去3x2-5x+1…”,他误将减去3x2-5x+1写为加上3x2-5x+1,得出的结果是5x2+3x-7。求出这道题的正确结果。
提示:a2-13ab+9b2-5=(a2-ab)-3(4ab-3b2)-5
答案:-1
提示:先设被减数为A,可由已知求出多项式A,再计算A-(3x2-5x+1)
谢
谢
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
