13.2 第2课时 用坐标轴表示轴对称 (共23张PPT)
文档属性
| 名称 | 13.2 第2课时 用坐标轴表示轴对称 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第十三章
轴对称
13.2
第2课时
用坐标表示轴对称
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
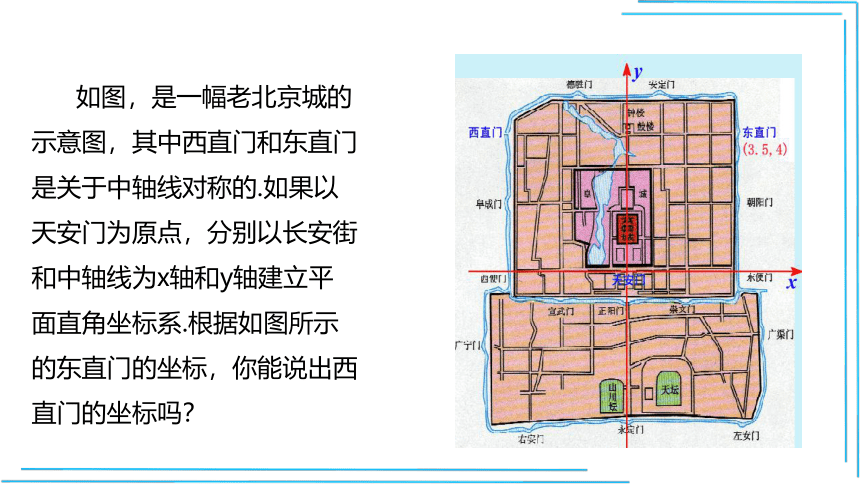
一位外国游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
猜一猜
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
获取新知
知识点一:关于x轴对称的点
x
y
O
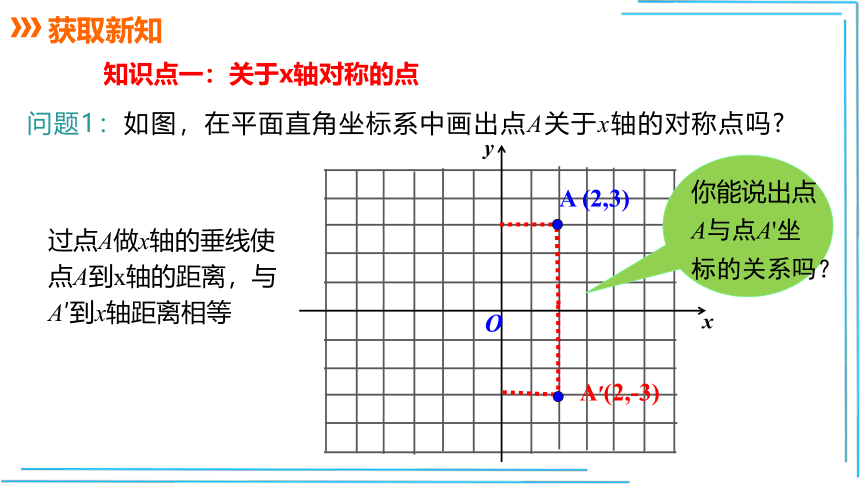
问题1:如图,在平面直角坐标系中画出点A关于x轴的对称点吗?
A
(2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
过点A做x轴的垂线使点A到x轴的距离,与A′到x轴距离相等
x
y
O
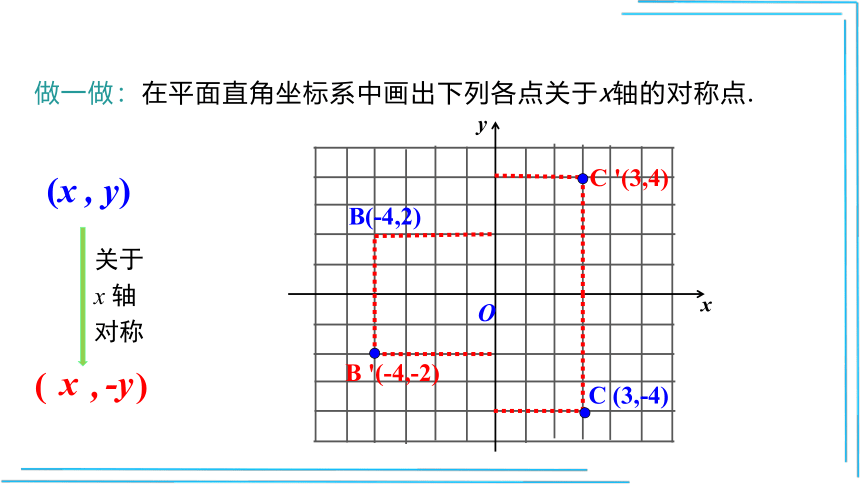
做一做:在平面直角坐标系中画出下列各点关于x轴的对称点.
C
(3,-4)
C
'(3,4)
B(-4,2)
B
'(-4,-2)
(x
,
y)
关于
x
轴
对称
(
,
)
x
-y
知识要点
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
点(x,y)关于x轴对称的点的坐标为(x,-y)
练
习
1.点P(-5,
6)与点Q关于x轴对称,则点Q的坐标为__________.
(-
5
,
-6
)
-2
5
2.点M(a,
-5)与点N(-2,
b)关于x轴对称,则a=_____,b
=_____.
知识点二:关于y轴对称的点
问题2:如图,在平面直角坐标系中画出点A关于y轴的对称点吗?
x
y
O
A
(2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
过点A做y轴的垂线使点A到y轴的距离,与A′到y轴距离相等
x
y
O
做一做:在平面直角坐标系中画出下列各点关于y轴的对称点.
C
(3,-4)
C
'(3,4)
B(-4,2)
B
'(-4,-2)
(x
,
y)
关于
y轴
对称
(
,
)
-x
y
知识要点
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
点(x,y)关于y轴对称的点的坐标为(-x,y)
1.点P(-5,
6)与点Q关于y轴对称,则点Q的坐标为_______.
2.点M(a,
-5)与点N(-2,
b)关于y轴对称,则a=_____,
b
=_____.
(5
,
6
)
2
-5
练
习
例题讲解
例1
[教材补充例题]分别写出下列各点关于x轴和y轴对称的点的坐标:(-2,3),(1,-2),(-2,-4),(0,2).
[解析]关于x轴对称的点的横坐标不变,纵坐标互为相反数;关于y轴对称的点的横坐标互为相反数,纵坐标不变.
解:点(-2,3),(1,-2),(-2,-4),(0,2)关于x轴对称的点的坐标分别为(-2,-3),(1,2),(-2,4),(0,-2);
点(-2,3),(1,-2),(-2,-4),(0,2)关于y轴对称的点的坐标分别为(2,3),(-1,-2),(2,-4),(0,2).
关于坐标轴对称的点的坐标规律的“简记法”
横轴对称,横不变纵变;纵轴对称,纵不变横变.
归纳总结
例题讲解
例2
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),
B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
C
D
A
′
B
′
C
′
D
′
A
′
B
′
C
′
D
′
O
在直角坐标系中画关于坐标轴对称的图形的“四字诀”
(1)找:在直角坐标系中,找出已知图形中的一些特殊点(如多
边形的顶点),写出它们的坐标;
(2)求:求出这些特殊点的对应点的坐标;
(3)描:根据所求坐标,描出对应点;
(4)连:顺次连接这些对应点,就可以得到这个图形的轴对称
图形.
归纳总结
随堂演练
D
1.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )
A.(3,2)
B.(-2,-3)
C.(-2,3)
D.(2,-3)
2.在平面直角坐标系中,点A(1,2)关于y轴对称的点为B(a,2),则a=________.
3.若点A(x+2,3)与点B(-5,y+7)关于x轴对称,则x=________,y=________.
-1
-7
-10
4.
已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2016的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
5.
已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a的取值范围.
解:依题意得P点在第四象限,
解得
即a的取值范围是
课堂小结
用坐标表示轴对称
关于坐标轴对称的点的坐标特征
在坐标系中作已知图形的对称图形
关于x轴对称,横同纵反;关于y轴对称,横反纵同
关键要明确点关于x轴、y轴对称点的坐标变化规律,然后正确描出对称点的位置
https://www.21cnjy.com/help/help_extract.php
第十三章
轴对称
13.2
第2课时
用坐标表示轴对称
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
一位外国游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
猜一猜
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
获取新知
知识点一:关于x轴对称的点
x
y
O
问题1:如图,在平面直角坐标系中画出点A关于x轴的对称点吗?
A
(2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
过点A做x轴的垂线使点A到x轴的距离,与A′到x轴距离相等
x
y
O
做一做:在平面直角坐标系中画出下列各点关于x轴的对称点.
C
(3,-4)
C
'(3,4)
B(-4,2)
B
'(-4,-2)
(x
,
y)
关于
x
轴
对称
(
,
)
x
-y
知识要点
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
点(x,y)关于x轴对称的点的坐标为(x,-y)
练
习
1.点P(-5,
6)与点Q关于x轴对称,则点Q的坐标为__________.
(-
5
,
-6
)
-2
5
2.点M(a,
-5)与点N(-2,
b)关于x轴对称,则a=_____,b
=_____.
知识点二:关于y轴对称的点
问题2:如图,在平面直角坐标系中画出点A关于y轴的对称点吗?
x
y
O
A
(2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
过点A做y轴的垂线使点A到y轴的距离,与A′到y轴距离相等
x
y
O
做一做:在平面直角坐标系中画出下列各点关于y轴的对称点.
C
(3,-4)
C
'(3,4)
B(-4,2)
B
'(-4,-2)
(x
,
y)
关于
y轴
对称
(
,
)
-x
y
知识要点
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
点(x,y)关于y轴对称的点的坐标为(-x,y)
1.点P(-5,
6)与点Q关于y轴对称,则点Q的坐标为_______.
2.点M(a,
-5)与点N(-2,
b)关于y轴对称,则a=_____,
b
=_____.
(5
,
6
)
2
-5
练
习
例题讲解
例1
[教材补充例题]分别写出下列各点关于x轴和y轴对称的点的坐标:(-2,3),(1,-2),(-2,-4),(0,2).
[解析]关于x轴对称的点的横坐标不变,纵坐标互为相反数;关于y轴对称的点的横坐标互为相反数,纵坐标不变.
解:点(-2,3),(1,-2),(-2,-4),(0,2)关于x轴对称的点的坐标分别为(-2,-3),(1,2),(-2,4),(0,-2);
点(-2,3),(1,-2),(-2,-4),(0,2)关于y轴对称的点的坐标分别为(2,3),(-1,-2),(2,-4),(0,2).
关于坐标轴对称的点的坐标规律的“简记法”
横轴对称,横不变纵变;纵轴对称,纵不变横变.
归纳总结
例题讲解
例2
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),
B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
C
D
A
′
B
′
C
′
D
′
A
′
B
′
C
′
D
′
O
在直角坐标系中画关于坐标轴对称的图形的“四字诀”
(1)找:在直角坐标系中,找出已知图形中的一些特殊点(如多
边形的顶点),写出它们的坐标;
(2)求:求出这些特殊点的对应点的坐标;
(3)描:根据所求坐标,描出对应点;
(4)连:顺次连接这些对应点,就可以得到这个图形的轴对称
图形.
归纳总结
随堂演练
D
1.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )
A.(3,2)
B.(-2,-3)
C.(-2,3)
D.(2,-3)
2.在平面直角坐标系中,点A(1,2)关于y轴对称的点为B(a,2),则a=________.
3.若点A(x+2,3)与点B(-5,y+7)关于x轴对称,则x=________,y=________.
-1
-7
-10
4.
已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2016的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
5.
已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a的取值范围.
解:依题意得P点在第四象限,
解得
即a的取值范围是
课堂小结
用坐标表示轴对称
关于坐标轴对称的点的坐标特征
在坐标系中作已知图形的对称图形
关于x轴对称,横同纵反;关于y轴对称,横反纵同
关键要明确点关于x轴、y轴对称点的坐标变化规律,然后正确描出对称点的位置
https://www.21cnjy.com/help/help_extract.php
