2.复数的基本概念 教案 2022届高三数学一轮复习备考(Word无答案)
文档属性
| 名称 | 2.复数的基本概念 教案 2022届高三数学一轮复习备考(Word无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 136.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 19:56:48 | ||
图片预览


文档简介
2.1
复数基本概念
【知识点】
1.虚数单位:满足
的数 称为虚数单位.
2.复数:可以写成 的数,此形式称为复数的代数表示,其中复数的实部为
,虚部为
;
复数z是实数虚部
,
复数z称为虚数虚部
,
复数z称为纯虚数实部 且虚部
;
由复数构成的集合称为复数集,记为 ={
|
}.
3.复数的分类
复数
4.相关概念
⑴z=a+bi(a、b∈R)的模(或称绝对值)记为|z|=
.
⑵z与互为共轭复数z与的实部 且虚部互为
“z=a+bi(a、b∈R)= ”.
结论:z·=|z|2.
⑶z1=z2z1的实部 z2的实部且z1的虚部 z2的虚部;
结论:不全是实数的两个复数不能比较大小.
⑷z∈Rz
; z≠0,则z是纯虚数z2
0z+= .
【应用点】
1.在表格中写出对应复数的实部与虚部、共轭复数
z
z的实部
z的虚部
z的共轭复数
-1+5i
0
-i
(1+i)(2-i)
2.在表格中写出对应复数的共轭复数、模
z
z的共轭复数
|z|
1+2i+i3
(1+i)2-2(1+i)
(3-2i)i
3.当m为何实数时,复数z=m2-1+(m2+3m+2)i是(1)实数?(2)纯虚数?
4.关于x的方程3x2-x-1=10i-ix-2ix2有实数根,求实数a的值.
5.复数z与(z+2)2-8i均是纯虚数,求z,
6.复数z1、z2满足|z1|=|z2|=2,z1+z2=+i,求|z1-z2|.
7.复数z1=sinθ+2i,z2=1+icosθ,求的最小值.
【核心点】
1.理清复数有关概念,可正确求共轭复数、模;
2.复数相等实现虚数问题实数化(等价转化思想或转化化归).
2.2
复数的运算
【知识点】
1.设,
z1+z2== ;z1-z2== ;
结论:= .
z1·z2== ;== .
(n∈Z).
2.复数加减乘除的共轭运算
设C、C,则:
= ;= ;= ;= .
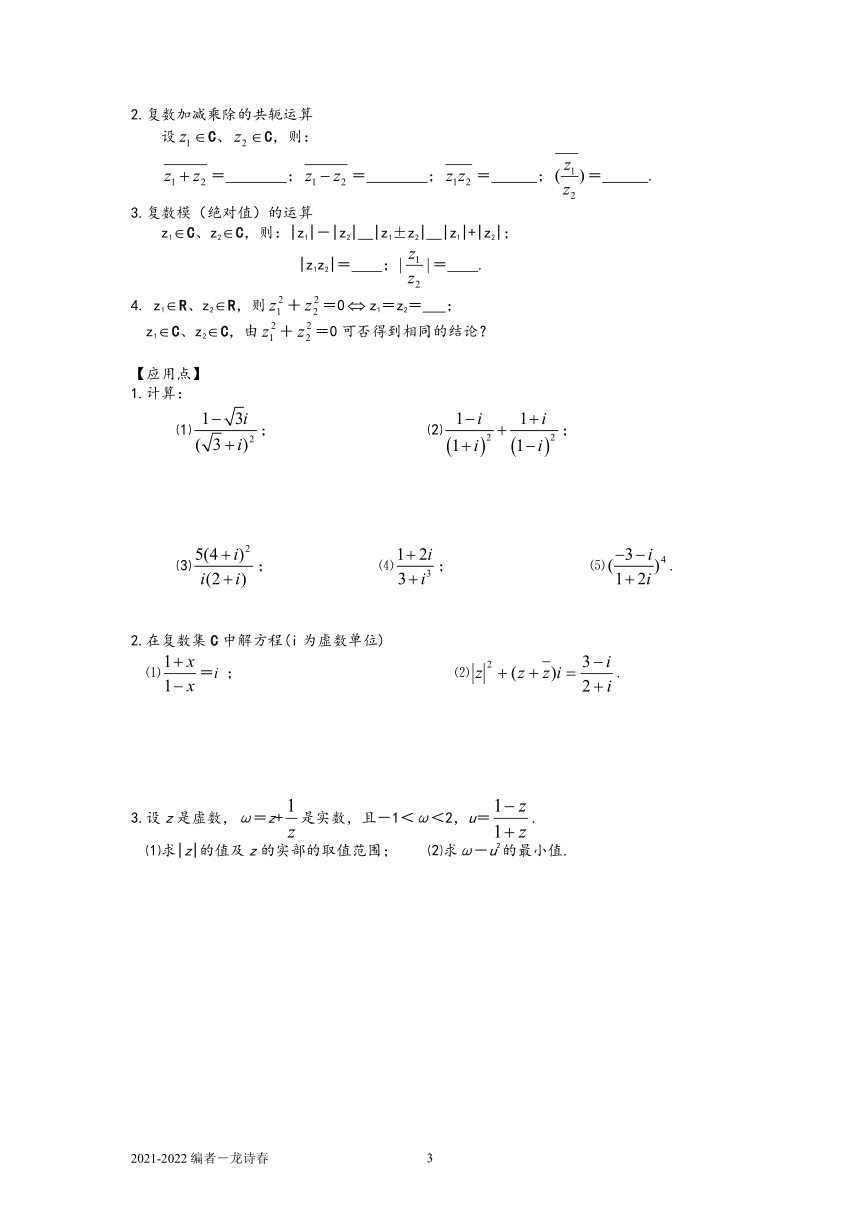
3.复数模(绝对值)的运算
z1C、z2C,则:|z1|-|z2|
|z1±z2| |z1|+|z2|;
|z1z2|= ;= .
z1R、z2R,则+=0z1=z2=
;
z1C、z2C,由+=0可否得到相同的结论?
【应用点】
1.计算:
⑴; ⑵;
⑶; ⑷; ⑸.
2.在复数集C中解方程(i为虚数单位)
⑴=i
; ⑵.
3.设z是虚数,ω=z+是实数,且-1<ω<2,u=.
⑴求|z|的值及z的实部的取值范围; ⑵求ω-u2的最小值.
4.⑴(多选题)z1C、z2C,zC,下列结论正确的是( )
A.若R,则zR
B.若z1×z2R,则z1=
C.若z2R,则zR
D.若zR,则R
⑵(多选题)z1C、z2C,下列结论正确的是( )
A.若|z1-z2|=0,则=
B.若z1=,则=z2
C.若|z1|=|z2|,则z1=z2
D.|z1|=|z2|,则z12=z22
【核心点】
复数的四则运算、共轭运算、模运算.
2.3
复数的几何意义
【知识点】
1.复数的几何面孔
用来表示复数的坐标平面称为
,其中x轴称为
,其上的点表示的复数是
;y轴(除去原点)称为
,其上的点表示的复数是
.
复数z=x+yi(x、y∈R)点Z(x,y)向量=(x,y),因而复数的加减法向量的加减法.
一些点的轨迹方程的复数形式
⑴z0=a+bi,a、b、r是实常数,且r>0,zC,z在复平面上对应点P,则|z-z0|=r点P的轨迹是 .
⑵z1=a+bi,z2=c+di,a、b、c、d是实常数,zC,z在复平面上对应点P,则|z-z1|=|z-z2|点P的轨迹是 .
⑶z1=-c,z2=c,c、a是大于0的实常数,a>c,zC,z在复平面上对应点P,则|z-z1|+|z-z2|=2a点P的轨迹是 .
【应用点】
1.在复平面内,复数-1的共轭复数所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在复平面内,复数z=5+m(i-1)(mR)对应的点不可能位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.在复平面内,复数z对应的点的坐标是(1,-2),则i·=( )
A.1+2i
B.-2+i
C.1-2i
D.-2-i
4.若z是复数,|z
+2-2i|=1,则|z-2-2i|的最小值是( )
A.2
B.3
C.4
D.5
5.已知|z|=1,则|z+|+|z-6|最小值是( )
A.6
B.37
C.5
D.6
6.已知z是复数,z+2i,均为实数(i是虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
7.z+=1,求|z+1|+|z-i|的取值范围.
【核心点】
1.复数的几何面孔;
2.通过复数的代数表示使复数问题转化为实数问题(转化化归思想).2021-2022编者-龙诗春
复数基本概念
【知识点】
1.虚数单位:满足
的数 称为虚数单位.
2.复数:可以写成 的数,此形式称为复数的代数表示,其中复数的实部为
,虚部为
;
复数z是实数虚部
,
复数z称为虚数虚部
,
复数z称为纯虚数实部 且虚部
;
由复数构成的集合称为复数集,记为 ={
|
}.
3.复数的分类
复数
4.相关概念
⑴z=a+bi(a、b∈R)的模(或称绝对值)记为|z|=
.
⑵z与互为共轭复数z与的实部 且虚部互为
“z=a+bi(a、b∈R)= ”.
结论:z·=|z|2.
⑶z1=z2z1的实部 z2的实部且z1的虚部 z2的虚部;
结论:不全是实数的两个复数不能比较大小.
⑷z∈Rz
; z≠0,则z是纯虚数z2
0z+= .
【应用点】
1.在表格中写出对应复数的实部与虚部、共轭复数
z
z的实部
z的虚部
z的共轭复数
-1+5i
0
-i
(1+i)(2-i)
2.在表格中写出对应复数的共轭复数、模
z
z的共轭复数
|z|
1+2i+i3
(1+i)2-2(1+i)
(3-2i)i
3.当m为何实数时,复数z=m2-1+(m2+3m+2)i是(1)实数?(2)纯虚数?
4.关于x的方程3x2-x-1=10i-ix-2ix2有实数根,求实数a的值.
5.复数z与(z+2)2-8i均是纯虚数,求z,
6.复数z1、z2满足|z1|=|z2|=2,z1+z2=+i,求|z1-z2|.
7.复数z1=sinθ+2i,z2=1+icosθ,求的最小值.
【核心点】
1.理清复数有关概念,可正确求共轭复数、模;
2.复数相等实现虚数问题实数化(等价转化思想或转化化归).
2.2
复数的运算
【知识点】
1.设,
z1+z2== ;z1-z2== ;
结论:= .
z1·z2== ;== .
(n∈Z).
2.复数加减乘除的共轭运算
设C、C,则:
= ;= ;= ;= .
3.复数模(绝对值)的运算
z1C、z2C,则:|z1|-|z2|
|z1±z2| |z1|+|z2|;
|z1z2|= ;= .
z1R、z2R,则+=0z1=z2=
;
z1C、z2C,由+=0可否得到相同的结论?
【应用点】
1.计算:
⑴; ⑵;
⑶; ⑷; ⑸.
2.在复数集C中解方程(i为虚数单位)
⑴=i
; ⑵.
3.设z是虚数,ω=z+是实数,且-1<ω<2,u=.
⑴求|z|的值及z的实部的取值范围; ⑵求ω-u2的最小值.
4.⑴(多选题)z1C、z2C,zC,下列结论正确的是( )
A.若R,则zR
B.若z1×z2R,则z1=
C.若z2R,则zR
D.若zR,则R
⑵(多选题)z1C、z2C,下列结论正确的是( )
A.若|z1-z2|=0,则=
B.若z1=,则=z2
C.若|z1|=|z2|,则z1=z2
D.|z1|=|z2|,则z12=z22
【核心点】
复数的四则运算、共轭运算、模运算.
2.3
复数的几何意义
【知识点】
1.复数的几何面孔
用来表示复数的坐标平面称为
,其中x轴称为
,其上的点表示的复数是
;y轴(除去原点)称为
,其上的点表示的复数是
.
复数z=x+yi(x、y∈R)点Z(x,y)向量=(x,y),因而复数的加减法向量的加减法.
一些点的轨迹方程的复数形式
⑴z0=a+bi,a、b、r是实常数,且r>0,zC,z在复平面上对应点P,则|z-z0|=r点P的轨迹是 .
⑵z1=a+bi,z2=c+di,a、b、c、d是实常数,zC,z在复平面上对应点P,则|z-z1|=|z-z2|点P的轨迹是 .
⑶z1=-c,z2=c,c、a是大于0的实常数,a>c,zC,z在复平面上对应点P,则|z-z1|+|z-z2|=2a点P的轨迹是 .
【应用点】
1.在复平面内,复数-1的共轭复数所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在复平面内,复数z=5+m(i-1)(mR)对应的点不可能位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.在复平面内,复数z对应的点的坐标是(1,-2),则i·=( )
A.1+2i
B.-2+i
C.1-2i
D.-2-i
4.若z是复数,|z
+2-2i|=1,则|z-2-2i|的最小值是( )
A.2
B.3
C.4
D.5
5.已知|z|=1,则|z+|+|z-6|最小值是( )
A.6
B.37
C.5
D.6
6.已知z是复数,z+2i,均为实数(i是虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
7.z+=1,求|z+1|+|z-i|的取值范围.
【核心点】
1.复数的几何面孔;
2.通过复数的代数表示使复数问题转化为实数问题(转化化归思想).2021-2022编者-龙诗春
同课章节目录
