9.三角函数与解三角形 教案 2022届高三数学一轮复习备考(Word无答案)
文档属性
| 名称 | 9.三角函数与解三角形 教案 2022届高三数学一轮复习备考(Word无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 20:04:39 | ||
图片预览




文档简介
9.1
角的概念与
【知识点】
1.任意角:一条射线绕着其
旋转形成角,
旋转形成的角称为零角,
旋转形成的角称为正角,
旋转形成的角称为负角。
2.角的度量
⑴角度制:圆周
,每一等分弧所对的
角的大小为1°。
⑵弧度制:
半径长的弧所对的
角的大小为1弧度,记为1rad。
⑶圆的弧长公式:
;扇形面积公式:
。
⑷角度制与弧度制的相互转化:
。
⑸填写表格
角度
0°
30°
45°
60°
90°
120°
135°
150°
210°
225°
弧度
3.⑴与角终边相同的角的集合是
;
角与角终边相同-=
。
⑵角的终边在x轴上=
;
角的终边在y轴上=
;
角的终边在坐标轴上=
;
角的终边在第一象限=
;
角的终边第二象限=
;
角的终边第三象限=
;
角的终边第四象限=
。
【应用点】
1.⑴(多选题)下列命题正确的是(
)
A.第四象限有一些角是锐角
B.任何一个象限都有负角
C.钝角是第二象限角
D.终边在坐标轴上的角的集合是{β|β=k·90°,kZ}
⑵(多选题)下列角的终边与角37°的终边在同一直线上的有(
)
A.-143°
B.-37°
C.379°
D.757°
⑶(多选题)下列结论正确的是(
)
A.-1485°=-10
B.-150°=-rad
C.rad=67°30/
D.长度等于其所在圆的内接正方形的边长的一段圆弧所对的圆心角为rad
⑷(多选题)下列结论正确的是(
)
A.β=k·360°+θ且α=m·360°-θ(k、mZ)β与α的终边关于y轴对称
B.β与α的终边关于y轴对称β+α=+2k(kZ)
C.β与α的终边相同β-α的终边在y轴的非负半轴上
D.α=k+(-1)k·(kZ),则α是第一象限或第二象限角
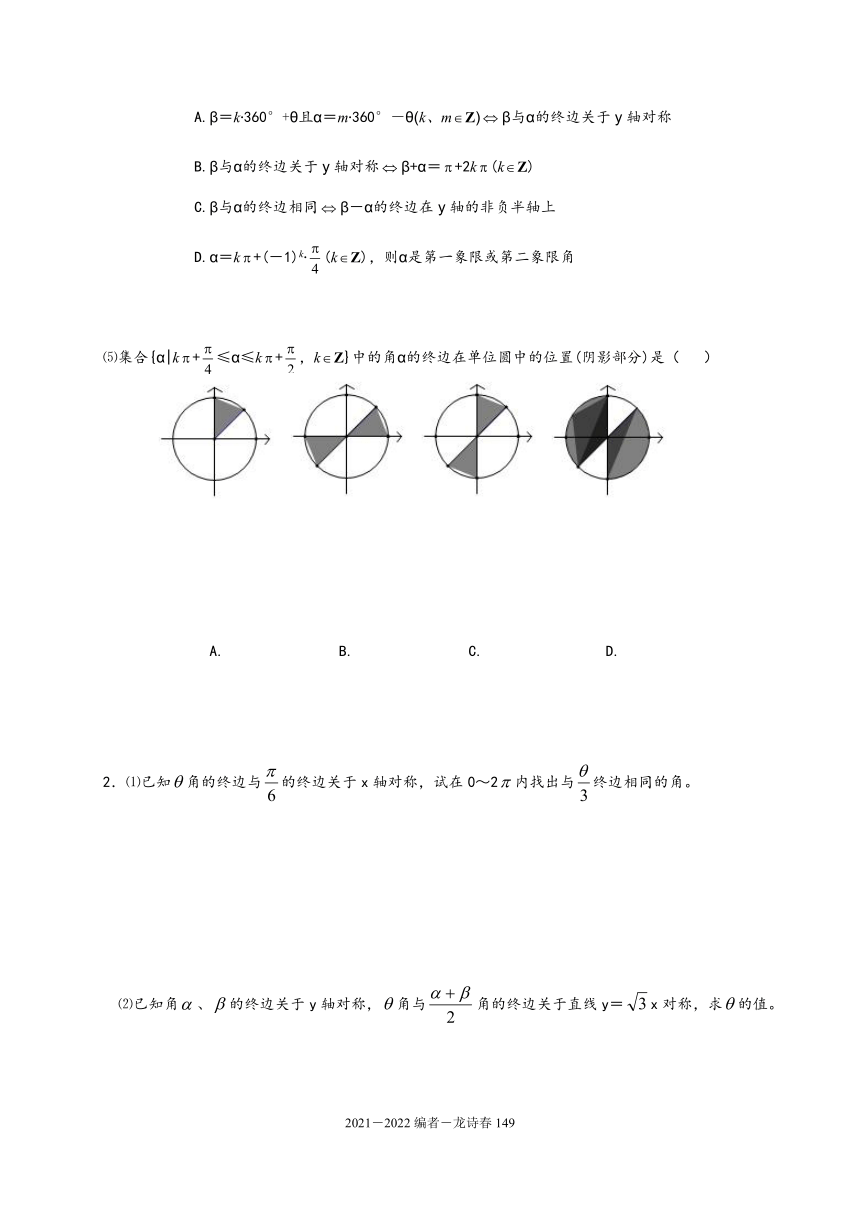
⑸集合{α|k+≤α≤k+,kZ}中的角α的终边在单位圆中的位置(阴影部分)是(
)
A.
B.
C.
D.
2.⑴已知角的终边与的终边关于x轴对称,试在0~2内找出与终边相同的角。
⑵已知角、的终边关于y轴对称,角与角的终边关于直线y=x对称,求的值。
⑶如果是第三象限的角,那么-、、2是第几象限的角?
3.已知一扇形的中心角是,所在圆的半径为R。
⑴若=60°,R=10
cm,求扇形的弧长及该弧所在的弓形面积;
⑵若扇形的周长是一定值C(C>0),当为多少时,该扇形有最大面积。
【核心点】
1.终边相同的角、象限角、角的两种度量制及转换;
2.扇形的弧长、面积的计算
9.2
任意角的三角函数定义
【知识点】
1.点P(a,b)是角终边上异于原点的任意一点,则点P到原点的距离r=
,
sin=
,cos=
,tan=
。
角x的终边与圆>0)的交点为P,则点P的坐标是(
)。
2.三角函数值的符号
3.填写表格
0
sin
cos
tan
【应用点】
1.⑴已知角α的终边过点P(-2m,8),且cosα=,则tanα的值为(
)
A.
B.
C.-
D.前三个选项都不对
⑵已知点P(sin,cos)落在角θ的终边上,且θ(0,2),则θ的值为(
)
A.
B.
C.
D.
⑶若α为第四象限角,则(
)
A.cos2α>0
B.
cos2α<0
C.sin2α>0
D.sin2α<0
⑷“θ为第一象限或第四象限角”是“cosθ>0”的(
)
A.充分不必要条件
B.
必要不充分条件
C.充要条件
D.不充分不必要条件
⑸设是第三象限角,且是( )
A.第一象限
B.第二象限 C.第三象限 D.第四象限
⑹如果是第一象限角,那么恒有(
)
A.
B.
C.
D.
2.已知P(4t,-3t)(t≠0)是角的终边上一点,求2sin+cos的值。
3.如果角的终边在直线5x+12y=0上,求sin、cos、tan的值。
4.借助于图形证明:若0<<,则sin<【核心点】
三角函数定义,三角函数值的符号与角的象限的关系
9.3
同角关系
【知识点】
同角关系
。
已知sin=m,求cos,tan:
已知tan=m,求sin,cos:
【应用点】
1.⑴(
)
A.第一象限
B.第二象限 C.第三象限 D.第四象限
⑵已知,且是第二象限角,则应满足的条件是(
)
A. B. C. D.
⑶若则=(
)
A.
B.2
C.
D.
⑷“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
2.若,求下列各式的值
⑴;
⑵。
3.若-<α<0,且,求tanα的值。
4.化简
⑴;
⑵cos4+sin2+sin2cos2-+tan4;
⑶;
⑷sinα+cosα(α为第三象限角)。
【核心点】
1.同角关系式及其变式;
2.正余弦成双的数(±,±)、(±,±)、(±,±)、(±,±)等等
9.4
诱导公式
【知识点】
1.sin(-)=
,cos(-)=
,tan(-)=
。
2.sin(-)=
,cos(-)=
,tan(-)=
。
3.sin(+)=
,cos(+)=
,tan(+)=
。
4.sin(2-)=
,cos(2-)=
,tan(2-)=
。
5.sin(2k+)=
,cos(2k+)=
,tan(2k+)=
。(k∈Z)
6.sin(-)=
,cos(-)=
,tan(-)=
。
7.sin(+)=
,cos(+)=
,tan(+)=
。
8.sin(-)=
,cos(-)=
,tan(-)=
。
9.sin(+)=
,cos(+)=
,tan(+)=
。
+(k∈Z)的三角函数值与角的三角函数值的关系是“
”。
诱导公式的作用是:
。
【应用点】
1.⑴sin585°的值为(
)
A.
B.
C.
D.
⑵等于(
)
A.sin2-cos2
B.cos2-sin2
C.±(sin2-cos2)
D.sin2+cos2
⑶已知cos(+α)=,且-<α<-,则cos(-α)等于(
)
A.
B.-
C.
D.-
⑷已知tan130°=m,则sin50°的值为(
)
A.-
B.
C.
D.-
⑸已知cos(-α)=-,且0<α<,则tan(+α)等于(
)
A.
B.±
C.±
D.前三个选项都不对
2.求下列三角函数的值
⑴;⑵sin420°cos330°+sin(-690°)cos(-660°)。
3.化简下列各式
⑴;
⑵tan(27°-)·tan(49°-)·tan(63°+)·tan(139°-)。
【核心点】
1.熟悉诱导公式,可正确运用诱导公式将任意角三角函数转化为[0,]内角的三角函数;
2.三看:一看角,二看名称,三看运算
9.5
和、差角公式
【知识点】
1.sin(+)=
,cos(+)=
,
tan(+)=
。
2.sin(-)=
,cos(-)=
,tan(-)=
。
变形:tan+tan=
;tan-tan=
。
3.a·sin+b·cos=
(其中a2+b2≠0)。
【应用点】
1.⑴sin163°sin223°+sin253°sin313°等于(
)
A.-
B.
C.-
D.
⑵化简等于
(
)
A.
B.
C.
D.
⑶的值是(
)
A.
B.
C.
D.
⑷若3sinx-cosx=2sin(x+φ),φ∈(-π,π),则φ等于(
)
A.-
B.
C.
D.-
⑸函数的最大值是(
)
A.
B.
C.7
D.8
⑹(
)
A.2
B.4
C.8
D.16
⑺已知x0是函数f(x)=sinx+2cosx的最大值点,则sinx0=(
)
A.
B.
C.
D.
2.⑴已知sin(-)sin(-+)+cos(-)sin(5-)=-,是第四象限角,求cos(-+)及tan(-)的值;
⑵已知cos(-)=,sin(+)=-,∈(,),∈(0,),求sin(+)的值;
⑶已知sin(+)+sin=-,-<<0,求sin的值;
⑷设cos(-)=-,sin(-β)=,且<<π,0<β<,求cos(+β)。
【核心点】
1.两角和与差的三角函数公式及其变式;
2.三看:一看角,二看名称,三看运算
9.6
倍角公式
【知识点】
1.sin2=
,cos2=
=
=
,
tan2=
。
2.变形:
⑴sin·cos=
,sin·cos=
。
⑵降幂:sin2=
,cos2=
;
sin2=
,cos2=
。
⑶升幂:1±sin=
,1+cos=
,
1-cos=
。
【应用点】
1.⑴若则θ是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
⑵下列各式中,值为的是
(
)
A.
sin15°cos15°
B.
C.
D.
⑶若270°<α<360°,化简的结果是(
)
A.sin
B.-sin
C.cos
D.-cos
⑷已知-<α<,且sin(α+)=,则cos(2α+)=(
)
A.-
B.
C.±
D.前三个选项都不对
⑸已知cos(α-)=-,则sin(2α-3)=(
)
A.-
B.
C.±
D.前三个选项都不对
2.⑴已知sin=-,180°<<270°,求sin2、cos的值;
⑵已知sin(-x)=,0<x<,求的值;
⑶求的值;
⑷已知,且、,求
的值。
3.化简⑴sin2+cos2(+)+sincos(+);
⑵。
【核心点】
1.二倍角公式及其变式;
2.三看:一看角,二看名称,三看运算
9.7
化简
【知识点】
三角式化简与求值常用思路
⑴角的变换:观察各角之间的和、差、倍、半关系,寻找已知角与未知角的联系,化异角为同角,化未知为已知,化非特殊角为特殊角。
⑵函数名称变换:观察条件与结论、数学式各函数名称之间的差异,化异名为同名,化切割为正余弦,化复杂为简单。
⑶运算结构变化:观察运算特点,或重新分组,或移项,或变除为乘,或求差和等,实现数学式向有关公式的运算形式转化。
⑷次数变化:升幂与降次,常用倍角公式:sin·cos=sin2,sin·cos=sin2,sin2=(1-cos2),cos2=(1+cos2),sin2=(1-cos),cos2=(1+cos)。1±sin=(sin±cos)2,1+cos=2
cos2,1-cos=2sin2。
⑸常数代换:1=sin2+cos2=cos0=sin=tan=-tan2。
三看原则:一看角,二看名称,三看运算
【应用点】
1.化简
⑴;
⑵cos8x-sin8x+sin2x·sin4x。
⑶tan+tan(+)+。
2.化简
⑴(tan10°-)·;
⑵--64cos210°;
⑶-4cos10°。
9.8
求值
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.求下列各式的值
⑴;
⑵+4sin210°。
2.已知sin(+)=,sin(-)=,求的值。
3.、为锐角,且3sin2+2sin2=1,3sin2-2sin2=0,求+2的值。
4.已知cosα=,cos(α-β)=,且0<β<α<,求tan2α的值以及β的值。
9.9
证明
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.
⑴证明-2cos(-)=-;
⑵已知+=1,求证tan2=tan·tan。
2.已知sin=m·sin(2+),其中m≠0,2+≠k,求证tan(+)=tan。
9.10
三角恒等变换综合
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.⑴αR,sinα+cosα=,则tanα=(
)
A.
B.-
C.
D.前三个选项都不对
⑵若x(0,),且+=2,则sin(2x+)=(
)
A.
B.-
C.
D.-
⑶若tanα=2tan,则=(
)
A.1
B.2
C.3
D.4
2.⑴△ABC中,B=60°,AC=,则AB+2BC的最大值是
。
⑵α、β(0,),且sinβ=2cos(α+β)sinα,若tan(α+β)=3,则tanα=
。
⑶已知tan(α+β)=4,tan(α-β)=2,则sin4α=
。
⑷已知α、β(0,),tan(α+β)=2tanα,则tanβ的最大值是
。
9.11
正弦定理
【知识点】
1.三角形中角的关系:A+B+C=
。
sin(A+B)=
,cos(A+B)=
,
sin=
,cos=
,
sin2(A+B)=
,cos2(A+B)=
。
2.正弦定理:
。
变式:
。
3.三角形的面积公式
⑴
;
⑵
。
【应用点】
1.⑴在△ABC中,A:B:C=4:1:1,则a:b:c等于(
)
A.4:1:1
B.3:1:1
C.2:1:1
D.:1:1
⑵在△ABC中,由已知条件解三角形,其中有两解的是(
)
A.
B.
C.
D.
⑶在△ABC中,内角A、B、C所对的边长分别为a、b、c,若a·sinBcosC+c·sinBcosA=b,且a>b,则B等于(
)
A.
B.
C.
D.
⑷在△ABC中,内角A、B、C所对的边长分别为a、b、c,且A=2B,a=b,则cosB等于(
)
A.
B.
C.
D.
⑸在△ABC中,内角A、B、C所对的边长分别为a、b、c,面积为S,若2S+a2=(b+c)2,则sinB等于(
)
A.
B.
C.
D.
⑹在△ABC中,若,则△ABC是(
)
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
⑺在△ABC中,内角A、B、C所对的边长分别为a、b、c,△ABC的面积为4,且2bcosA+a=2c,a+c=8,则其周长为(
)
A.10
B.12
C.8+
D.8+2
⑻△ABC的内角A、B、C所对的边长分别为a、b、c,若B=2A,cosAcosBcosC>0,则的取值范围是(
)
A.(,)
B.(,)
C.(,)
D.(,)
2.在△ABC中,已知=,求角A的值。
3.在△ABC中,内角A、B、C所对的边长分别为a、b、c。已知b·sinA=a·cos(B-)。
⑴求角B的大小;
⑵设a=2,c=3,求b和sin(2A-B)的值。
4.在△ABC中,求证=。
5.在△ABC中,内角A、B、C所对的边长分别为a、b、c,若a2+b2=6,cos(A-B)cosC=,求△ABC的外接圆半径。
【核心点】
正弦定理实现三角形的边、内角的正弦、外接圆半径的转换
9.12
余弦定理
【知识点】
余弦定理:
;
;
;
变式:
;
;
;
△ABC中角C为锐角充要条件是:
;
△ABC中角C为直角充要条件是:
;
△ABC中角C为钝角充要条件是:
。
【应用点】
1.⑴△ABC中,a、b、c分别为内角A、B、C的对边,如果a、b、c成等差数列,B=30°,△ABC的面积为,那么b等于( )
A.
B.1+
C.
D.2+
⑵△ABC中,a、b、c分别为内角A、B、C的对边,若a2+b2=2c2,则cosC的最小值为(
)
A.
B.
C.
D.-
⑶△ABC中,a、b、c分别为内角A、B、C的对边,若cosC=,b·cosA+a·cosB=2,则△ABC的外接圆面积为(
)
A.4
B.8
C.9
D.36
⑷△ABC中,a、b、c分别为内角A、B、C的对边,已知--=1,△ABC的外接圆半径为3,则a=(
)
A.2
B.3
C.3
D.2
⑸△ABC中,若AC=BC,C=,△ABC的面积S△ABC=sin2A,则S△ABC=(
)
A.
B.
C.
D.2
⑹△ABC中,a、b、c分别为内角A、B、C的对边,sinA+sinB=2sinC,b=3,当内角C最大时,△ABC的面积等于(
)
A.
B.
C.
D.
⑺△ABC内角A、B、C的对边分别为a、b、c,且=,若a+b=4,则c的取值范围是(
)
A.(0,4)
B.[2,4)
C.[1,4)
D.(2,4]
⑻△ABC中,D为边BC的中点,E为边BC上一点,且AE=AC=BE,DE=1,若cosC=,则△ABC的面积等于
。
2.△ABC内角A、B、C的对边分别为a、b、c,已知c=,△ABC的面积为,且tanA+tanB=tanA·tanB-.求a+b的值。
3.在△ABC中,AB=,cosB=,AC边上的中线BD=,求sinA的值。
【核心点】
余弦定理实现三角形的边、内角的余弦的转换
9.13
解三角形综合
【应用点】
1.⑴△ABC内角A、B、C满足sin2A+sin2B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
⑵在△ABC中,内角A的平分线交边BC于D,AB=4,AC=8,BD=2,则△ABD的面积是(
)
A.
B.3
C.1
D.3
⑶在△ABC中,已知+cosC=0,tanA=,则tanB=(
)
A.
B.2
C.
D.
⑷△ABC内角A、B、C的对边分别为a、b、c,=cosB+cosC,=8,则△ABC的周长的最小值是(
)
A.3
B.4
C.3+3
D.4+4
⑸锐角△ABC的内角A、B、C的对边分别为a、b、c,△ABC的面积是S,若sin(A+C)=,则tanC+的最小值为(
)
A.1
B.
C.2
D.2
⑹在平面四边形ABCD中,∠A=60°,∠C=∠B=75°,BC=,则AB的取值范围是
。
⑺锐角△ABC中,BC=2,sinB+sinC=2sinA,则中线AD长的取值范围是
。
⑻锐角△ABC的内角A、B、C的对边分别为a、b、c,+=6cosC,则+=
。
⑼锐角△ABC中,若sinA=2sinB·sinC,则tanA·tanB·tanC的最小值是
。
2.在△ABC中,a·tanA+b·tanB=(a+b)tan,判断△ABC的形状。
3.已知△ABC中,2(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为.
⑴求∠C;
⑵求△ABC面积的最大值。
4.△ABC内角A、B、C的对边分别为a、b、c,已知a=3,c=,B=45°.
⑴求sinC的值;
⑵在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值。
5.△ABC内角A、B、C的对边分别为a、b、c,已知a=4,ab·sinAsinC=c·sinB.
⑴若bc=16,求b2+c2的值;
⑵若B=2A,求b.
【核心点】
找边角关系,边角互化
9.14
三角形中三角函数问题
【知识点】
1.△ABC是等腰三角形的充要条件是
。
△ABC是直角三角形的充要条件是
。
2.解三角形通常运用正弦定理、余弦定理、三角形面积公式以及内角三角函数关系。
【应用点】
1.⑴在△ABC中,角A、B、C所对的边分别是、、,且BC边上的高为,则的最大值为(
)
A.
B
C
2
D
4
⑵、、分别是△ABC的三个内角A、B、C所对的边,则是A=2B的(
)
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.不充分不必要条件
⑶在锐角△ABC中,BC=1,B=2A,则的值等于
,AC的取值范围为
。
⑷△ABC中,BC=4,CA=5,AB=6,(将CA=5变为C
A边上的中线长为呢)则sin6+cos6=
。
3.设△ABC的内角A、B、C的对边长分别为a、b、c,且3+3-3=4bc
。
⑴求sinA的值;
⑵求的值。
4.△ABC的内角A、B、C的对边长分别为a、b、c,且cos(C+B)cos(C-B)=cos2A-sinCsinB.
⑴求A;
⑵若a=3,求b+2c的最大值。
5.△ABC的内角A、B、C的对边长分别为a、b、c,且=,B为锐角。
⑴求A;
⑵若a=3,c=1,△ABC内有一点M,∠AMB=∠BMC=∠CMA=,求MA+MB+MC的值。
【核心点】
寻找边角关系
9.15
正弦、余弦函数的图像与性质
【知识点】
正弦函数y=sinx
余弦函数y=cosx
图
像
定义域
值
域
最
值
周期性
奇偶性
单调性
对称轴
对称中心
【应用点】
1.⑴若,则下列命题中正确的是( )
A.
B.
C.
D.
⑵函数f(x)=sinx-cosx,x[-,0]的单调递增区间是( )
A.
B.
C.
D.
⑶若0≤α≤2,sinα>cosα,则α的取值范围是(
)
A.
B.
C.
D.
2.求定义域
⑴f(x)=log(1-2cosx)(2sinx+1);
⑵f(x)=.
3.设函数f(x)=sin(x+)(k∈N﹡),已知当x在任意两个整数间变化时(包括整数本身),至少存在一个x1和一个x2,使f(x1)=1,且f(x2)=-1,求k的最小值。
4.设函数f(x)=a·sinx+cosx,若存在x0∈(0,),使f(x0)=a成立,求实数a的取值范围。
5.已知函数f(x)=2sin(x+)-2cosx,x[,]。
⑴若sinx0=,求f(x0)的值;
⑵求函数f(x)的值域。
【核心点】
正弦、余弦函数的图像,注意限制图像的特征直线
9.16
正切函数的图像与性质
【知识点】
y=tanx
图
像
定义域
值
域
最
值
周期性
奇偶性
单调性
渐近线
对称中心
【应用点】
1.⑴函数f(x)=tan(x+)的单调增区间为(
)
A.(k-,k+)
B.(k,(k+1))
C.(k-,k+)
D.(k-,k+)(k∈Z)
⑵设α、β(-,),那么“α<β”是“tanαA.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑶若将函数y=tan(x+)(>0)的图像向右平移个单位长度后,与函数y=tan(x+)的图像重合,则的最小值为( )
A.
B.
C.
D.
⑷设,,,则( )
A.
B.
C.
D.
2.⑴若,则函数的最大值为
。
⑵若x∈(0,
),则2tanx+tan(-x)的最小值为
。
⑶已知函数f(x)=sinx+tanx,项数为27的等差数列{an}满足an∈(-,),且公差d≠0,若f(a1)+f(a2)+…+f(a27)=0,则当k=
时,f(ak)=0。
⑷函数f(x)=tan(x+)+tan(x-)的奇偶性是
。
【核心点】
正切函数的图像,注意图像的特征直线
9.17
三角函数值域问题
【知识点】
1.y=sinx,y=cosx的值域是
;y=a·sinx+b·cosx的值域是
。
2.y=tanx的值域是
。
3.y=a·sinx+b(或y=a·cosx+b)的值域是
。
4.y=a·sin2x+b·sinx+c(或y=a·cos2x+b·cosx+c)的值域转化为求
的值域。
【应用点】
1.求下列函数的最值
⑴y=;
⑵;
⑶y=3sin(x+20°)+5sin(x+80°);
⑷y=。
2.求下列函数的值域。
⑴f(x)=;
⑵f(x)=2cos(+x)+2cosx;
⑶f(x)=,x[,];
⑷f(x)=,x[,];
⑸f(x)=,x[0,2];
⑹f(x)=2cosx+cos2x;
⑺f(x)=3sin2x-2sin2x+2sinx-cosx,x[0,]。
3.△ABC中,sinA=,求cosB+cosC的取值范围。
【核心点】
等价转化思想
9.18
三角函数的周期性
【知识点】
1.y=sinx、y=cosx的最小正周期是
,周期是
。
f(x)=A·sin(x+)+B或f(x)=A·cos(x+)+B(≠0)的最小正周期是
,周期是
。
f(x)=A·|sin(x+)|+B或f(x)=A·|cos(x+)|+B(≠0)的最小正周期是
,周期是
。
2.y=tanx的最小正周期是
,周期是
。
f(x)=A·tan(x+)+B(≠0)的最小正周期是
,周期是
。
f(x)=A·|tan(x+)|+B(≠0)的最小正周期是
,周期是
。
3.一般地,若周期函数f(x)的周期为T,则函数a·f(x)+b(ab≠O)的周期是
,函数f(x+)(≠0)的周期是
。
【应用点】
1.求下列函数的最小正周期
⑴f(x)=sin(2x-)+2sin2(x-);
⑵f(x)=2+;
⑶;
⑷。
2.⑴已知函数f(x)=sin(x-)cos(x-)(>0)的一个单调递减区间是[-,0],则=(
)
A.1
B.2
C.4
D.6
⑵(多选题)已知函数f(x)=sin(x+)(>0)在区间[0,2]上有且仅有5个零点,则下列结论正确的有(
)
A.f(x)在区间(0,2)上有且仅有3个极大值点
B.f(x)在区间(0,2)上有且仅有2个极小值点
C.f(x)在区间(0,)上单调递增
D.的取值范围是[,)
⑶将函数f(x)=2sin(x+)的图像向右平移个单位长度后,所得图像与原图像重合,则正数的最小值为(
)
A.1
B.2
C.3
D.4
⑷数列{an}的通项为an=n2(cos2-sin2),其前n项和为Sn,则S30=(
)
A.470
B.490
C.495
D.510
⑸设函数f(x)=sin2x+b·sinx+c,则f(x)的最小正周期(
)
与b有关且与c有关
B.与b有关且与c无关
C.与b无关且与c无关
D.与b无关且与c有关
【核心点】
周期性在图像上体现为隔相同距离图像重复
9.19
三角函数对称性
【知识点】
填写表格
y=sinx
y=cosx
y=A·sin(x+)
y=tanx
对称轴
对称中心
递增区间
递减区间
【应用点】
1.⑴已知函数f(x)=a·sinx-b·cosx的最大值在x=处取到,则f(x+)是(
)
A.奇函数且关于点(,0)中心对称
B.偶函数且关于点(,0)中心对称
C.奇函数且关于点(,0)中心对称
D.偶函数且关于点(,0)中心对称
⑵函数y=3cos(2x+)的图像关于点(,0)对称,那么的最小值为(
)
A.
B.
C.
D.
⑶f(x)=sin(2x+φ)+cos(2x+φ)的图像关于原点对称的充要条件是( )
A.φ=2kπ-,k∈Z
B.φ=kπ-,k∈Z
C.φ=2kπ-,k∈Z
D.φ=kπ-,k∈Z
⑷函数y=的图像与y=1+2sinx(-4≤x≤2)的图像所有交点的横坐标之和等于(
)
A.-1
B.-2
C.-4
D.-6
⑸实数x、y满足,则x+y=(
)
A.0
B.2
C.4
D.6
⑹若函数f(x)=4cos(x+φ)对任意的xR都有f(-x)=f(+x),设函数g(x)=sin(x+φ)-2,则g()的值是(
)
A.1
B.-2
C.
D.-5或3
⑺若函数f(x)=a·sinx-cosx图像的一条对称轴为直线x=,且f(x1)·f(x2)=-4,则|x1+x2|的最小值为(
)
A.0
B.
C.
D.
⑻已知函数f(x)=3sin(x-)(>0)和g(x)=2cos(2x+)+1的图象的对称轴完全相同。若x[0,],则f(x)的取值范围是
。
⑼设f(x)=x3+3(x2+x+sinx),则f(1-)+f(-3)=
。
⑽已知函数f(x)=+x+sinx,若正实数a、b满足f(4a)+f(b-9)=0,则+的最小值为
。
2.已知函数,.若是函数图象的一条对称轴,求的值.
3.已知函数f(x)=为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为,求f()的值.
【核心点】
对称性的图像特征与数学式的关系
9.20
三角函数单调性
【应用点】
1.⑴已知函数f(x)=sinx+cosx(>0),y=f(x)的图像与直线y=2的两个相邻交点的距离等于,则f(x)的单调递增区间是(
)
A.
B.
C.
D.
⑵设函数,若,则下列不等式一定成立的是( )
A.
B.
C.
D.
⑶设是一个钝角三角形的两个锐角,则下列四个不等式中不正确的是(
)
A.
B.
C.
D.
⑷若f(x)=cosx-sinx在[-a,a]是减函数,则a的最大值是(
)
A.
B.
C.
D.
⑸设f/(x)是定义在(-,0)∪(0,)上的偶函数f(x)的导函数,且f/()=0,当x(0,)时,不等式f/(x)·sinx-f(x)·cosx>0恒成立。若a=-2f(-),b=2f(-),c=f(),则a、b、c的大小关系是(
)
A.cB.bC.aD.b⑹函数f(x)=2sinx(cosx-sinx)的单调递减区间是
。
⑺若函数f(x)=a·sinx+cos2x在区间(,)上是减函数,则a的取值范围是
。
⑻若函数f(x)=4sin(-x)sinx+cos(2-2x)在区间[-,]上单调递增,则正数的最大值为
。
2.比较下列各组值的大小
⑴sin、cos5;
⑵、。
3.设函数f(x)=sin(2x+φ)(-<φ<0),y=f(x)图象的一条对称轴是直线x=。
⑴求函数y=f(x)的单调增区间;
⑵证明直线5x-2y+c=0与函数y=f(x)的图象不相切。
4.已知函数f(x)=sin(x+φ)(>0,0≤φ≤)是R上的偶函数,其图象关于点M(,0)对称,且在区间[0,]上是单调函数,求和φ的值。
【核心点】
三角函数的单调性与周期性的关系
9.21
三角函数图像变换
【知识点】
1.y=A·sin(x+)的有关概念
y=A·sin(x+)(A>0,>0,x∈[0,+∞)
)表示一个振动量时,振幅是
,周期是
,频率是
,相位是
,初相是
。
2.作y=A·sin(x+)的图像
⑴五点法作简图
x+
x
y
⑵变换法作图:
振幅变换:y=sinx→y=A·sinx:
。
相位变换:y=A·sinx→y=A·sin(x+):
。
相位变换:y=A·sinx→y=A·sin(x+):
。
周期变换:y=A·sin(x+)→y=A·sin(x+):
。
【应用点】
1.⑴(多选题)为了得到函数y=sin(2x-)的图像,只需把函数y=sin(2x+)的图像(
)
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移最小个长度单位
D.向右平移最小个长度单位
⑵将函数y=sinx的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是(
)
A.y=sin(2x-)
B.y=sin(2x-)
C.y=sin(x-)
D.y=sin(x-)
⑶(多选题)为了得到函数y=sin(2x-)的图像,只需把函数y=cos2x的图像(
)
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移最小个长度单位
D.向右平移最小个长度单位
⑷将函数f(x)=2sinx·cosx-2cos2x+1的图像向左或向右平移a个单位后,得到函数g(x)的图像,若g(x)=g(-x),则实数a的最小值为(
)
A.
B.
C.
D.
⑸已知函数f(x)=2cossin(-)+sin2+sincos(>0)在[0
,]上单调,且f(0)+f()=0,若将函数f(x)的图像向左平移(>0)个单位长度后得到的函数是偶函数,则的最小值为(
)
A.
B.
C.
D.
2.已知函数f(x)=sin2x+sinx·cosx+2cos2x,xR。
⑴求函数f(x)的最小正周期和单调增区间;
⑵函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
【核心点】
三角形式函数的图像左右平移与周期性的关系
9.22
与三角函数相关的零点问题
【知识点】
y=sinx
y=cosx
y=A·sin(x+)
y=tanx
零点
【应用点】
1.函数f(x)=cos(3x+)在[0
,]内的零点个数为
。
2.定义在区间[0
,3]上的函数f(x)=sin2x-cosx的零点个数为
。
3.定义在区间[0
,2]上的函数f(x)=sin3x-sinx的所有零点之和为(
)
A.5
B.6
C.7
D.8
4.已知函数f(x)=cos2+sinx-(>0,xR),若在区间(
,2)上没有零点,则的取值范围是(
)
A.(0,)
B.(0,]
C.(0,]
D.(0,]∪[,]
5.已知函数f(x)=4sin(2x-),x[0
,],若函数F(x)=f(x)-3的所有零点依次记为x1、x2、x3、…、xn,且x1)
A.
B.445
C.455
D.
6.已知函数f(x)=sin(x+)(>0,[0
,])的图像经过点(0,),若关于x的方程f(x)=-1在[
,]上恰有一个实数解,则的取值范围是(
)
A.[,)
B.[,8]
C.[,20]
D.[,20]
7.已知函数f(x)=cosx,函数g(x)的图像可以由函数f(x)的图像先向右平移个单位长度,再将所得函数图像保持纵坐标不变,横坐标变为原来的(>0)倍得到,若函数在(,)上没有零点,则的取值范围是(
)
A.(0,]
B.[,]
C.(,]
D.(0,]
8.已知定义在R上的偶函数f(x)满足f(4-x)=f(x),且当x(-1,3]时f(x)=,则g(x)=f(x)-lg|x|的零点个数是(
)
A.9
B.10
C.18
D.20
9.已知函数f(x)=|sinx|-kx(x≥0,kR)有且只有3个零点,设此3个零点中的最大值为x0,则=
。
【核心点】
对称性、周期性对零点的影响
9.23
三角型函数解析式
【知识点】
求y=A·sin(x+)+B的解析式的步骤:求A、B:确定函数最大值M与最小值m,若A>0,则A+B=M,-A+B=m;若A<0,则-A+B=M,A+B=m→求:确定函数的最小正周期T,则=→求:由特定函数值确定。
【应用点】
1.如图,函数y=2cos(x+θ)(xR,0≤θ≤)的图象与y轴交于点(0,),且在该点处切线的斜率为-2。
(1)求θ和的值;
(2)已知点A(,0),点P是该函数图象上一点,Q(x0,y0)是PA的中点,当y0=,x0[,]时,求x0的值。
2.已知函数f(x)=A·sin(x+)(xR,A>0,>0,0<<)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为M(,-2)。
⑴求f(x)的解析式;
⑵当x[,],求f(x)的值域。
3.已知函数f(x)=其中,。
⑴若coscos-sinsin=0,求的值;
⑵在⑴的条件下,若函数f(x)的图像的相邻两条对称轴之间的距离等于,求函数f(x)的解析式;并求最小正实数,使得函数f(x)的图像象左平移个单位所对应的函数是偶函数。
4.已知函数的图象上有一个最低点(,1),将图象上每个点的纵坐标不变,横坐标缩小到原来的,然后将所得图象向左平移一个单位得到f(x)的图象,若方程f(x)=3的所有正根依次成为一个公差为3的等差数列,求f(x)的解析式。
5.函数f(x)=其中,,f(x)在一个周期内的图像经过A(-,0)、B(-,-01)、C(,0)、D(,1)四个点中的三个点,求f(x)的解析式。
【核心点】
注意求解的顺序
9.24
三角函数与导数结合问题
【应用点】
1.已知函数f(x)=ex-ax+sinx-1。
⑴当a=2时,求函数f(x)的单调区间;
⑵当1≤a<2时,证明函数f(x)有2个零点。
2.已知函数f(x)=sinx+aln(x+b),g(x)是f(x)的导函数。
⑴若a>0,当b=1时,函数g(x)在(,4)内有唯一的极小值,求a的取值范围;
⑵若a=-1,13.已知函数f(x)=ae-x+cosx(aR)。
⑴若函数f(x)在(-,0)上是单调函数,求a的取值范围;
⑵当时,x0为函数f(x)在(0,)上的零点,求证-x0<。
2021-2022编者-龙诗春76
角的概念与
【知识点】
1.任意角:一条射线绕着其
旋转形成角,
旋转形成的角称为零角,
旋转形成的角称为正角,
旋转形成的角称为负角。
2.角的度量
⑴角度制:圆周
,每一等分弧所对的
角的大小为1°。
⑵弧度制:
半径长的弧所对的
角的大小为1弧度,记为1rad。
⑶圆的弧长公式:
;扇形面积公式:
。
⑷角度制与弧度制的相互转化:
。
⑸填写表格
角度
0°
30°
45°
60°
90°
120°
135°
150°
210°
225°
弧度
3.⑴与角终边相同的角的集合是
;
角与角终边相同-=
。
⑵角的终边在x轴上=
;
角的终边在y轴上=
;
角的终边在坐标轴上=
;
角的终边在第一象限=
;
角的终边第二象限=
;
角的终边第三象限=
;
角的终边第四象限=
。
【应用点】
1.⑴(多选题)下列命题正确的是(
)
A.第四象限有一些角是锐角
B.任何一个象限都有负角
C.钝角是第二象限角
D.终边在坐标轴上的角的集合是{β|β=k·90°,kZ}
⑵(多选题)下列角的终边与角37°的终边在同一直线上的有(
)
A.-143°
B.-37°
C.379°
D.757°
⑶(多选题)下列结论正确的是(
)
A.-1485°=-10
B.-150°=-rad
C.rad=67°30/
D.长度等于其所在圆的内接正方形的边长的一段圆弧所对的圆心角为rad
⑷(多选题)下列结论正确的是(
)
A.β=k·360°+θ且α=m·360°-θ(k、mZ)β与α的终边关于y轴对称
B.β与α的终边关于y轴对称β+α=+2k(kZ)
C.β与α的终边相同β-α的终边在y轴的非负半轴上
D.α=k+(-1)k·(kZ),则α是第一象限或第二象限角
⑸集合{α|k+≤α≤k+,kZ}中的角α的终边在单位圆中的位置(阴影部分)是(
)
A.
B.
C.
D.
2.⑴已知角的终边与的终边关于x轴对称,试在0~2内找出与终边相同的角。
⑵已知角、的终边关于y轴对称,角与角的终边关于直线y=x对称,求的值。
⑶如果是第三象限的角,那么-、、2是第几象限的角?
3.已知一扇形的中心角是,所在圆的半径为R。
⑴若=60°,R=10
cm,求扇形的弧长及该弧所在的弓形面积;
⑵若扇形的周长是一定值C(C>0),当为多少时,该扇形有最大面积。
【核心点】
1.终边相同的角、象限角、角的两种度量制及转换;
2.扇形的弧长、面积的计算
9.2
任意角的三角函数定义
【知识点】
1.点P(a,b)是角终边上异于原点的任意一点,则点P到原点的距离r=
,
sin=
,cos=
,tan=
。
角x的终边与圆>0)的交点为P,则点P的坐标是(
)。
2.三角函数值的符号
3.填写表格
0
sin
cos
tan
【应用点】
1.⑴已知角α的终边过点P(-2m,8),且cosα=,则tanα的值为(
)
A.
B.
C.-
D.前三个选项都不对
⑵已知点P(sin,cos)落在角θ的终边上,且θ(0,2),则θ的值为(
)
A.
B.
C.
D.
⑶若α为第四象限角,则(
)
A.cos2α>0
B.
cos2α<0
C.sin2α>0
D.sin2α<0
⑷“θ为第一象限或第四象限角”是“cosθ>0”的(
)
A.充分不必要条件
B.
必要不充分条件
C.充要条件
D.不充分不必要条件
⑸设是第三象限角,且是( )
A.第一象限
B.第二象限 C.第三象限 D.第四象限
⑹如果是第一象限角,那么恒有(
)
A.
B.
C.
D.
2.已知P(4t,-3t)(t≠0)是角的终边上一点,求2sin+cos的值。
3.如果角的终边在直线5x+12y=0上,求sin、cos、tan的值。
4.借助于图形证明:若0<<,则sin<
三角函数定义,三角函数值的符号与角的象限的关系
9.3
同角关系
【知识点】
同角关系
。
已知sin=m,求cos,tan:
已知tan=m,求sin,cos:
【应用点】
1.⑴(
)
A.第一象限
B.第二象限 C.第三象限 D.第四象限
⑵已知,且是第二象限角,则应满足的条件是(
)
A. B. C. D.
⑶若则=(
)
A.
B.2
C.
D.
⑷“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
2.若,求下列各式的值
⑴;
⑵。
3.若-<α<0,且,求tanα的值。
4.化简
⑴;
⑵cos4+sin2+sin2cos2-+tan4;
⑶;
⑷sinα+cosα(α为第三象限角)。
【核心点】
1.同角关系式及其变式;
2.正余弦成双的数(±,±)、(±,±)、(±,±)、(±,±)等等
9.4
诱导公式
【知识点】
1.sin(-)=
,cos(-)=
,tan(-)=
。
2.sin(-)=
,cos(-)=
,tan(-)=
。
3.sin(+)=
,cos(+)=
,tan(+)=
。
4.sin(2-)=
,cos(2-)=
,tan(2-)=
。
5.sin(2k+)=
,cos(2k+)=
,tan(2k+)=
。(k∈Z)
6.sin(-)=
,cos(-)=
,tan(-)=
。
7.sin(+)=
,cos(+)=
,tan(+)=
。
8.sin(-)=
,cos(-)=
,tan(-)=
。
9.sin(+)=
,cos(+)=
,tan(+)=
。
+(k∈Z)的三角函数值与角的三角函数值的关系是“
”。
诱导公式的作用是:
。
【应用点】
1.⑴sin585°的值为(
)
A.
B.
C.
D.
⑵等于(
)
A.sin2-cos2
B.cos2-sin2
C.±(sin2-cos2)
D.sin2+cos2
⑶已知cos(+α)=,且-<α<-,则cos(-α)等于(
)
A.
B.-
C.
D.-
⑷已知tan130°=m,则sin50°的值为(
)
A.-
B.
C.
D.-
⑸已知cos(-α)=-,且0<α<,则tan(+α)等于(
)
A.
B.±
C.±
D.前三个选项都不对
2.求下列三角函数的值
⑴;⑵sin420°cos330°+sin(-690°)cos(-660°)。
3.化简下列各式
⑴;
⑵tan(27°-)·tan(49°-)·tan(63°+)·tan(139°-)。
【核心点】
1.熟悉诱导公式,可正确运用诱导公式将任意角三角函数转化为[0,]内角的三角函数;
2.三看:一看角,二看名称,三看运算
9.5
和、差角公式
【知识点】
1.sin(+)=
,cos(+)=
,
tan(+)=
。
2.sin(-)=
,cos(-)=
,tan(-)=
。
变形:tan+tan=
;tan-tan=
。
3.a·sin+b·cos=
(其中a2+b2≠0)。
【应用点】
1.⑴sin163°sin223°+sin253°sin313°等于(
)
A.-
B.
C.-
D.
⑵化简等于
(
)
A.
B.
C.
D.
⑶的值是(
)
A.
B.
C.
D.
⑷若3sinx-cosx=2sin(x+φ),φ∈(-π,π),则φ等于(
)
A.-
B.
C.
D.-
⑸函数的最大值是(
)
A.
B.
C.7
D.8
⑹(
)
A.2
B.4
C.8
D.16
⑺已知x0是函数f(x)=sinx+2cosx的最大值点,则sinx0=(
)
A.
B.
C.
D.
2.⑴已知sin(-)sin(-+)+cos(-)sin(5-)=-,是第四象限角,求cos(-+)及tan(-)的值;
⑵已知cos(-)=,sin(+)=-,∈(,),∈(0,),求sin(+)的值;
⑶已知sin(+)+sin=-,-<<0,求sin的值;
⑷设cos(-)=-,sin(-β)=,且<<π,0<β<,求cos(+β)。
【核心点】
1.两角和与差的三角函数公式及其变式;
2.三看:一看角,二看名称,三看运算
9.6
倍角公式
【知识点】
1.sin2=
,cos2=
=
=
,
tan2=
。
2.变形:
⑴sin·cos=
,sin·cos=
。
⑵降幂:sin2=
,cos2=
;
sin2=
,cos2=
。
⑶升幂:1±sin=
,1+cos=
,
1-cos=
。
【应用点】
1.⑴若则θ是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
⑵下列各式中,值为的是
(
)
A.
sin15°cos15°
B.
C.
D.
⑶若270°<α<360°,化简的结果是(
)
A.sin
B.-sin
C.cos
D.-cos
⑷已知-<α<,且sin(α+)=,则cos(2α+)=(
)
A.-
B.
C.±
D.前三个选项都不对
⑸已知cos(α-)=-,则sin(2α-3)=(
)
A.-
B.
C.±
D.前三个选项都不对
2.⑴已知sin=-,180°<<270°,求sin2、cos的值;
⑵已知sin(-x)=,0<x<,求的值;
⑶求的值;
⑷已知,且、,求
的值。
3.化简⑴sin2+cos2(+)+sincos(+);
⑵。
【核心点】
1.二倍角公式及其变式;
2.三看:一看角,二看名称,三看运算
9.7
化简
【知识点】
三角式化简与求值常用思路
⑴角的变换:观察各角之间的和、差、倍、半关系,寻找已知角与未知角的联系,化异角为同角,化未知为已知,化非特殊角为特殊角。
⑵函数名称变换:观察条件与结论、数学式各函数名称之间的差异,化异名为同名,化切割为正余弦,化复杂为简单。
⑶运算结构变化:观察运算特点,或重新分组,或移项,或变除为乘,或求差和等,实现数学式向有关公式的运算形式转化。
⑷次数变化:升幂与降次,常用倍角公式:sin·cos=sin2,sin·cos=sin2,sin2=(1-cos2),cos2=(1+cos2),sin2=(1-cos),cos2=(1+cos)。1±sin=(sin±cos)2,1+cos=2
cos2,1-cos=2sin2。
⑸常数代换:1=sin2+cos2=cos0=sin=tan=-tan2。
三看原则:一看角,二看名称,三看运算
【应用点】
1.化简
⑴;
⑵cos8x-sin8x+sin2x·sin4x。
⑶tan+tan(+)+。
2.化简
⑴(tan10°-)·;
⑵--64cos210°;
⑶-4cos10°。
9.8
求值
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.求下列各式的值
⑴;
⑵+4sin210°。
2.已知sin(+)=,sin(-)=,求的值。
3.、为锐角,且3sin2+2sin2=1,3sin2-2sin2=0,求+2的值。
4.已知cosα=,cos(α-β)=,且0<β<α<,求tan2α的值以及β的值。
9.9
证明
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.
⑴证明-2cos(-)=-;
⑵已知+=1,求证tan2=tan·tan。
2.已知sin=m·sin(2+),其中m≠0,2+≠k,求证tan(+)=tan。
9.10
三角恒等变换综合
【知识点】
三看:一看角,二看名称,三看运算
【应用点】
1.⑴αR,sinα+cosα=,则tanα=(
)
A.
B.-
C.
D.前三个选项都不对
⑵若x(0,),且+=2,则sin(2x+)=(
)
A.
B.-
C.
D.-
⑶若tanα=2tan,则=(
)
A.1
B.2
C.3
D.4
2.⑴△ABC中,B=60°,AC=,则AB+2BC的最大值是
。
⑵α、β(0,),且sinβ=2cos(α+β)sinα,若tan(α+β)=3,则tanα=
。
⑶已知tan(α+β)=4,tan(α-β)=2,则sin4α=
。
⑷已知α、β(0,),tan(α+β)=2tanα,则tanβ的最大值是
。
9.11
正弦定理
【知识点】
1.三角形中角的关系:A+B+C=
。
sin(A+B)=
,cos(A+B)=
,
sin=
,cos=
,
sin2(A+B)=
,cos2(A+B)=
。
2.正弦定理:
。
变式:
。
3.三角形的面积公式
⑴
;
⑵
。
【应用点】
1.⑴在△ABC中,A:B:C=4:1:1,则a:b:c等于(
)
A.4:1:1
B.3:1:1
C.2:1:1
D.:1:1
⑵在△ABC中,由已知条件解三角形,其中有两解的是(
)
A.
B.
C.
D.
⑶在△ABC中,内角A、B、C所对的边长分别为a、b、c,若a·sinBcosC+c·sinBcosA=b,且a>b,则B等于(
)
A.
B.
C.
D.
⑷在△ABC中,内角A、B、C所对的边长分别为a、b、c,且A=2B,a=b,则cosB等于(
)
A.
B.
C.
D.
⑸在△ABC中,内角A、B、C所对的边长分别为a、b、c,面积为S,若2S+a2=(b+c)2,则sinB等于(
)
A.
B.
C.
D.
⑹在△ABC中,若,则△ABC是(
)
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
⑺在△ABC中,内角A、B、C所对的边长分别为a、b、c,△ABC的面积为4,且2bcosA+a=2c,a+c=8,则其周长为(
)
A.10
B.12
C.8+
D.8+2
⑻△ABC的内角A、B、C所对的边长分别为a、b、c,若B=2A,cosAcosBcosC>0,则的取值范围是(
)
A.(,)
B.(,)
C.(,)
D.(,)
2.在△ABC中,已知=,求角A的值。
3.在△ABC中,内角A、B、C所对的边长分别为a、b、c。已知b·sinA=a·cos(B-)。
⑴求角B的大小;
⑵设a=2,c=3,求b和sin(2A-B)的值。
4.在△ABC中,求证=。
5.在△ABC中,内角A、B、C所对的边长分别为a、b、c,若a2+b2=6,cos(A-B)cosC=,求△ABC的外接圆半径。
【核心点】
正弦定理实现三角形的边、内角的正弦、外接圆半径的转换
9.12
余弦定理
【知识点】
余弦定理:
;
;
;
变式:
;
;
;
△ABC中角C为锐角充要条件是:
;
△ABC中角C为直角充要条件是:
;
△ABC中角C为钝角充要条件是:
。
【应用点】
1.⑴△ABC中,a、b、c分别为内角A、B、C的对边,如果a、b、c成等差数列,B=30°,△ABC的面积为,那么b等于( )
A.
B.1+
C.
D.2+
⑵△ABC中,a、b、c分别为内角A、B、C的对边,若a2+b2=2c2,则cosC的最小值为(
)
A.
B.
C.
D.-
⑶△ABC中,a、b、c分别为内角A、B、C的对边,若cosC=,b·cosA+a·cosB=2,则△ABC的外接圆面积为(
)
A.4
B.8
C.9
D.36
⑷△ABC中,a、b、c分别为内角A、B、C的对边,已知--=1,△ABC的外接圆半径为3,则a=(
)
A.2
B.3
C.3
D.2
⑸△ABC中,若AC=BC,C=,△ABC的面积S△ABC=sin2A,则S△ABC=(
)
A.
B.
C.
D.2
⑹△ABC中,a、b、c分别为内角A、B、C的对边,sinA+sinB=2sinC,b=3,当内角C最大时,△ABC的面积等于(
)
A.
B.
C.
D.
⑺△ABC内角A、B、C的对边分别为a、b、c,且=,若a+b=4,则c的取值范围是(
)
A.(0,4)
B.[2,4)
C.[1,4)
D.(2,4]
⑻△ABC中,D为边BC的中点,E为边BC上一点,且AE=AC=BE,DE=1,若cosC=,则△ABC的面积等于
。
2.△ABC内角A、B、C的对边分别为a、b、c,已知c=,△ABC的面积为,且tanA+tanB=tanA·tanB-.求a+b的值。
3.在△ABC中,AB=,cosB=,AC边上的中线BD=,求sinA的值。
【核心点】
余弦定理实现三角形的边、内角的余弦的转换
9.13
解三角形综合
【应用点】
1.⑴△ABC内角A、B、C满足sin2A+sin2B
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
⑵在△ABC中,内角A的平分线交边BC于D,AB=4,AC=8,BD=2,则△ABD的面积是(
)
A.
B.3
C.1
D.3
⑶在△ABC中,已知+cosC=0,tanA=,则tanB=(
)
A.
B.2
C.
D.
⑷△ABC内角A、B、C的对边分别为a、b、c,=cosB+cosC,=8,则△ABC的周长的最小值是(
)
A.3
B.4
C.3+3
D.4+4
⑸锐角△ABC的内角A、B、C的对边分别为a、b、c,△ABC的面积是S,若sin(A+C)=,则tanC+的最小值为(
)
A.1
B.
C.2
D.2
⑹在平面四边形ABCD中,∠A=60°,∠C=∠B=75°,BC=,则AB的取值范围是
。
⑺锐角△ABC中,BC=2,sinB+sinC=2sinA,则中线AD长的取值范围是
。
⑻锐角△ABC的内角A、B、C的对边分别为a、b、c,+=6cosC,则+=
。
⑼锐角△ABC中,若sinA=2sinB·sinC,则tanA·tanB·tanC的最小值是
。
2.在△ABC中,a·tanA+b·tanB=(a+b)tan,判断△ABC的形状。
3.已知△ABC中,2(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为.
⑴求∠C;
⑵求△ABC面积的最大值。
4.△ABC内角A、B、C的对边分别为a、b、c,已知a=3,c=,B=45°.
⑴求sinC的值;
⑵在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值。
5.△ABC内角A、B、C的对边分别为a、b、c,已知a=4,ab·sinAsinC=c·sinB.
⑴若bc=16,求b2+c2的值;
⑵若B=2A,求b.
【核心点】
找边角关系,边角互化
9.14
三角形中三角函数问题
【知识点】
1.△ABC是等腰三角形的充要条件是
。
△ABC是直角三角形的充要条件是
。
2.解三角形通常运用正弦定理、余弦定理、三角形面积公式以及内角三角函数关系。
【应用点】
1.⑴在△ABC中,角A、B、C所对的边分别是、、,且BC边上的高为,则的最大值为(
)
A.
B
C
2
D
4
⑵、、分别是△ABC的三个内角A、B、C所对的边,则是A=2B的(
)
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.不充分不必要条件
⑶在锐角△ABC中,BC=1,B=2A,则的值等于
,AC的取值范围为
。
⑷△ABC中,BC=4,CA=5,AB=6,(将CA=5变为C
A边上的中线长为呢)则sin6+cos6=
。
3.设△ABC的内角A、B、C的对边长分别为a、b、c,且3+3-3=4bc
。
⑴求sinA的值;
⑵求的值。
4.△ABC的内角A、B、C的对边长分别为a、b、c,且cos(C+B)cos(C-B)=cos2A-sinCsinB.
⑴求A;
⑵若a=3,求b+2c的最大值。
5.△ABC的内角A、B、C的对边长分别为a、b、c,且=,B为锐角。
⑴求A;
⑵若a=3,c=1,△ABC内有一点M,∠AMB=∠BMC=∠CMA=,求MA+MB+MC的值。
【核心点】
寻找边角关系
9.15
正弦、余弦函数的图像与性质
【知识点】
正弦函数y=sinx
余弦函数y=cosx
图
像
定义域
值
域
最
值
周期性
奇偶性
单调性
对称轴
对称中心
【应用点】
1.⑴若,则下列命题中正确的是( )
A.
B.
C.
D.
⑵函数f(x)=sinx-cosx,x[-,0]的单调递增区间是( )
A.
B.
C.
D.
⑶若0≤α≤2,sinα>cosα,则α的取值范围是(
)
A.
B.
C.
D.
2.求定义域
⑴f(x)=log(1-2cosx)(2sinx+1);
⑵f(x)=.
3.设函数f(x)=sin(x+)(k∈N﹡),已知当x在任意两个整数间变化时(包括整数本身),至少存在一个x1和一个x2,使f(x1)=1,且f(x2)=-1,求k的最小值。
4.设函数f(x)=a·sinx+cosx,若存在x0∈(0,),使f(x0)=a成立,求实数a的取值范围。
5.已知函数f(x)=2sin(x+)-2cosx,x[,]。
⑴若sinx0=,求f(x0)的值;
⑵求函数f(x)的值域。
【核心点】
正弦、余弦函数的图像,注意限制图像的特征直线
9.16
正切函数的图像与性质
【知识点】
y=tanx
图
像
定义域
值
域
最
值
周期性
奇偶性
单调性
渐近线
对称中心
【应用点】
1.⑴函数f(x)=tan(x+)的单调增区间为(
)
A.(k-,k+)
B.(k,(k+1))
C.(k-,k+)
D.(k-,k+)(k∈Z)
⑵设α、β(-,),那么“α<β”是“tanα
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑶若将函数y=tan(x+)(>0)的图像向右平移个单位长度后,与函数y=tan(x+)的图像重合,则的最小值为( )
A.
B.
C.
D.
⑷设,,,则( )
A.
B.
C.
D.
2.⑴若,则函数的最大值为
。
⑵若x∈(0,
),则2tanx+tan(-x)的最小值为
。
⑶已知函数f(x)=sinx+tanx,项数为27的等差数列{an}满足an∈(-,),且公差d≠0,若f(a1)+f(a2)+…+f(a27)=0,则当k=
时,f(ak)=0。
⑷函数f(x)=tan(x+)+tan(x-)的奇偶性是
。
【核心点】
正切函数的图像,注意图像的特征直线
9.17
三角函数值域问题
【知识点】
1.y=sinx,y=cosx的值域是
;y=a·sinx+b·cosx的值域是
。
2.y=tanx的值域是
。
3.y=a·sinx+b(或y=a·cosx+b)的值域是
。
4.y=a·sin2x+b·sinx+c(或y=a·cos2x+b·cosx+c)的值域转化为求
的值域。
【应用点】
1.求下列函数的最值
⑴y=;
⑵;
⑶y=3sin(x+20°)+5sin(x+80°);
⑷y=。
2.求下列函数的值域。
⑴f(x)=;
⑵f(x)=2cos(+x)+2cosx;
⑶f(x)=,x[,];
⑷f(x)=,x[,];
⑸f(x)=,x[0,2];
⑹f(x)=2cosx+cos2x;
⑺f(x)=3sin2x-2sin2x+2sinx-cosx,x[0,]。
3.△ABC中,sinA=,求cosB+cosC的取值范围。
【核心点】
等价转化思想
9.18
三角函数的周期性
【知识点】
1.y=sinx、y=cosx的最小正周期是
,周期是
。
f(x)=A·sin(x+)+B或f(x)=A·cos(x+)+B(≠0)的最小正周期是
,周期是
。
f(x)=A·|sin(x+)|+B或f(x)=A·|cos(x+)|+B(≠0)的最小正周期是
,周期是
。
2.y=tanx的最小正周期是
,周期是
。
f(x)=A·tan(x+)+B(≠0)的最小正周期是
,周期是
。
f(x)=A·|tan(x+)|+B(≠0)的最小正周期是
,周期是
。
3.一般地,若周期函数f(x)的周期为T,则函数a·f(x)+b(ab≠O)的周期是
,函数f(x+)(≠0)的周期是
。
【应用点】
1.求下列函数的最小正周期
⑴f(x)=sin(2x-)+2sin2(x-);
⑵f(x)=2+;
⑶;
⑷。
2.⑴已知函数f(x)=sin(x-)cos(x-)(>0)的一个单调递减区间是[-,0],则=(
)
A.1
B.2
C.4
D.6
⑵(多选题)已知函数f(x)=sin(x+)(>0)在区间[0,2]上有且仅有5个零点,则下列结论正确的有(
)
A.f(x)在区间(0,2)上有且仅有3个极大值点
B.f(x)在区间(0,2)上有且仅有2个极小值点
C.f(x)在区间(0,)上单调递增
D.的取值范围是[,)
⑶将函数f(x)=2sin(x+)的图像向右平移个单位长度后,所得图像与原图像重合,则正数的最小值为(
)
A.1
B.2
C.3
D.4
⑷数列{an}的通项为an=n2(cos2-sin2),其前n项和为Sn,则S30=(
)
A.470
B.490
C.495
D.510
⑸设函数f(x)=sin2x+b·sinx+c,则f(x)的最小正周期(
)
与b有关且与c有关
B.与b有关且与c无关
C.与b无关且与c无关
D.与b无关且与c有关
【核心点】
周期性在图像上体现为隔相同距离图像重复
9.19
三角函数对称性
【知识点】
填写表格
y=sinx
y=cosx
y=A·sin(x+)
y=tanx
对称轴
对称中心
递增区间
递减区间
【应用点】
1.⑴已知函数f(x)=a·sinx-b·cosx的最大值在x=处取到,则f(x+)是(
)
A.奇函数且关于点(,0)中心对称
B.偶函数且关于点(,0)中心对称
C.奇函数且关于点(,0)中心对称
D.偶函数且关于点(,0)中心对称
⑵函数y=3cos(2x+)的图像关于点(,0)对称,那么的最小值为(
)
A.
B.
C.
D.
⑶f(x)=sin(2x+φ)+cos(2x+φ)的图像关于原点对称的充要条件是( )
A.φ=2kπ-,k∈Z
B.φ=kπ-,k∈Z
C.φ=2kπ-,k∈Z
D.φ=kπ-,k∈Z
⑷函数y=的图像与y=1+2sinx(-4≤x≤2)的图像所有交点的横坐标之和等于(
)
A.-1
B.-2
C.-4
D.-6
⑸实数x、y满足,则x+y=(
)
A.0
B.2
C.4
D.6
⑹若函数f(x)=4cos(x+φ)对任意的xR都有f(-x)=f(+x),设函数g(x)=sin(x+φ)-2,则g()的值是(
)
A.1
B.-2
C.
D.-5或3
⑺若函数f(x)=a·sinx-cosx图像的一条对称轴为直线x=,且f(x1)·f(x2)=-4,则|x1+x2|的最小值为(
)
A.0
B.
C.
D.
⑻已知函数f(x)=3sin(x-)(>0)和g(x)=2cos(2x+)+1的图象的对称轴完全相同。若x[0,],则f(x)的取值范围是
。
⑼设f(x)=x3+3(x2+x+sinx),则f(1-)+f(-3)=
。
⑽已知函数f(x)=+x+sinx,若正实数a、b满足f(4a)+f(b-9)=0,则+的最小值为
。
2.已知函数,.若是函数图象的一条对称轴,求的值.
3.已知函数f(x)=为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为,求f()的值.
【核心点】
对称性的图像特征与数学式的关系
9.20
三角函数单调性
【应用点】
1.⑴已知函数f(x)=sinx+cosx(>0),y=f(x)的图像与直线y=2的两个相邻交点的距离等于,则f(x)的单调递增区间是(
)
A.
B.
C.
D.
⑵设函数,若,则下列不等式一定成立的是( )
A.
B.
C.
D.
⑶设是一个钝角三角形的两个锐角,则下列四个不等式中不正确的是(
)
A.
B.
C.
D.
⑷若f(x)=cosx-sinx在[-a,a]是减函数,则a的最大值是(
)
A.
B.
C.
D.
⑸设f/(x)是定义在(-,0)∪(0,)上的偶函数f(x)的导函数,且f/()=0,当x(0,)时,不等式f/(x)·sinx-f(x)·cosx>0恒成立。若a=-2f(-),b=2f(-),c=f(),则a、b、c的大小关系是(
)
A.c
。
⑺若函数f(x)=a·sinx+cos2x在区间(,)上是减函数,则a的取值范围是
。
⑻若函数f(x)=4sin(-x)sinx+cos(2-2x)在区间[-,]上单调递增,则正数的最大值为
。
2.比较下列各组值的大小
⑴sin、cos5;
⑵、。
3.设函数f(x)=sin(2x+φ)(-<φ<0),y=f(x)图象的一条对称轴是直线x=。
⑴求函数y=f(x)的单调增区间;
⑵证明直线5x-2y+c=0与函数y=f(x)的图象不相切。
4.已知函数f(x)=sin(x+φ)(>0,0≤φ≤)是R上的偶函数,其图象关于点M(,0)对称,且在区间[0,]上是单调函数,求和φ的值。
【核心点】
三角函数的单调性与周期性的关系
9.21
三角函数图像变换
【知识点】
1.y=A·sin(x+)的有关概念
y=A·sin(x+)(A>0,>0,x∈[0,+∞)
)表示一个振动量时,振幅是
,周期是
,频率是
,相位是
,初相是
。
2.作y=A·sin(x+)的图像
⑴五点法作简图
x+
x
y
⑵变换法作图:
振幅变换:y=sinx→y=A·sinx:
。
相位变换:y=A·sinx→y=A·sin(x+):
。
相位变换:y=A·sinx→y=A·sin(x+):
。
周期变换:y=A·sin(x+)→y=A·sin(x+):
。
【应用点】
1.⑴(多选题)为了得到函数y=sin(2x-)的图像,只需把函数y=sin(2x+)的图像(
)
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移最小个长度单位
D.向右平移最小个长度单位
⑵将函数y=sinx的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是(
)
A.y=sin(2x-)
B.y=sin(2x-)
C.y=sin(x-)
D.y=sin(x-)
⑶(多选题)为了得到函数y=sin(2x-)的图像,只需把函数y=cos2x的图像(
)
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移最小个长度单位
D.向右平移最小个长度单位
⑷将函数f(x)=2sinx·cosx-2cos2x+1的图像向左或向右平移a个单位后,得到函数g(x)的图像,若g(x)=g(-x),则实数a的最小值为(
)
A.
B.
C.
D.
⑸已知函数f(x)=2cossin(-)+sin2+sincos(>0)在[0
,]上单调,且f(0)+f()=0,若将函数f(x)的图像向左平移(>0)个单位长度后得到的函数是偶函数,则的最小值为(
)
A.
B.
C.
D.
2.已知函数f(x)=sin2x+sinx·cosx+2cos2x,xR。
⑴求函数f(x)的最小正周期和单调增区间;
⑵函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
【核心点】
三角形式函数的图像左右平移与周期性的关系
9.22
与三角函数相关的零点问题
【知识点】
y=sinx
y=cosx
y=A·sin(x+)
y=tanx
零点
【应用点】
1.函数f(x)=cos(3x+)在[0
,]内的零点个数为
。
2.定义在区间[0
,3]上的函数f(x)=sin2x-cosx的零点个数为
。
3.定义在区间[0
,2]上的函数f(x)=sin3x-sinx的所有零点之和为(
)
A.5
B.6
C.7
D.8
4.已知函数f(x)=cos2+sinx-(>0,xR),若在区间(
,2)上没有零点,则的取值范围是(
)
A.(0,)
B.(0,]
C.(0,]
D.(0,]∪[,]
5.已知函数f(x)=4sin(2x-),x[0
,],若函数F(x)=f(x)-3的所有零点依次记为x1、x2、x3、…、xn,且x1
A.
B.445
C.455
D.
6.已知函数f(x)=sin(x+)(>0,[0
,])的图像经过点(0,),若关于x的方程f(x)=-1在[
,]上恰有一个实数解,则的取值范围是(
)
A.[,)
B.[,8]
C.[,20]
D.[,20]
7.已知函数f(x)=cosx,函数g(x)的图像可以由函数f(x)的图像先向右平移个单位长度,再将所得函数图像保持纵坐标不变,横坐标变为原来的(>0)倍得到,若函数在(,)上没有零点,则的取值范围是(
)
A.(0,]
B.[,]
C.(,]
D.(0,]
8.已知定义在R上的偶函数f(x)满足f(4-x)=f(x),且当x(-1,3]时f(x)=,则g(x)=f(x)-lg|x|的零点个数是(
)
A.9
B.10
C.18
D.20
9.已知函数f(x)=|sinx|-kx(x≥0,kR)有且只有3个零点,设此3个零点中的最大值为x0,则=
。
【核心点】
对称性、周期性对零点的影响
9.23
三角型函数解析式
【知识点】
求y=A·sin(x+)+B的解析式的步骤:求A、B:确定函数最大值M与最小值m,若A>0,则A+B=M,-A+B=m;若A<0,则-A+B=M,A+B=m→求:确定函数的最小正周期T,则=→求:由特定函数值确定。
【应用点】
1.如图,函数y=2cos(x+θ)(xR,0≤θ≤)的图象与y轴交于点(0,),且在该点处切线的斜率为-2。
(1)求θ和的值;
(2)已知点A(,0),点P是该函数图象上一点,Q(x0,y0)是PA的中点,当y0=,x0[,]时,求x0的值。
2.已知函数f(x)=A·sin(x+)(xR,A>0,>0,0<<)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为M(,-2)。
⑴求f(x)的解析式;
⑵当x[,],求f(x)的值域。
3.已知函数f(x)=其中,。
⑴若coscos-sinsin=0,求的值;
⑵在⑴的条件下,若函数f(x)的图像的相邻两条对称轴之间的距离等于,求函数f(x)的解析式;并求最小正实数,使得函数f(x)的图像象左平移个单位所对应的函数是偶函数。
4.已知函数的图象上有一个最低点(,1),将图象上每个点的纵坐标不变,横坐标缩小到原来的,然后将所得图象向左平移一个单位得到f(x)的图象,若方程f(x)=3的所有正根依次成为一个公差为3的等差数列,求f(x)的解析式。
5.函数f(x)=其中,,f(x)在一个周期内的图像经过A(-,0)、B(-,-01)、C(,0)、D(,1)四个点中的三个点,求f(x)的解析式。
【核心点】
注意求解的顺序
9.24
三角函数与导数结合问题
【应用点】
1.已知函数f(x)=ex-ax+sinx-1。
⑴当a=2时,求函数f(x)的单调区间;
⑵当1≤a<2时,证明函数f(x)有2个零点。
2.已知函数f(x)=sinx+aln(x+b),g(x)是f(x)的导函数。
⑴若a>0,当b=1时,函数g(x)在(,4)内有唯一的极小值,求a的取值范围;
⑵若a=-1,1
⑴若函数f(x)在(-,0)上是单调函数,求a的取值范围;
⑵当时,x0为函数f(x)在(0,)上的零点,求证-x0<。
2021-2022编者-龙诗春76
同课章节目录
