2022届高考数学一轮复习-立体几何讲义(Word无答案)
文档属性
| 名称 | 2022届高考数学一轮复习-立体几何讲义(Word无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 20:01:51 | ||
图片预览




文档简介
11.1
空间简单几何体的直观图、三视图
【知识点】
1.柱、锥、台、球的结构特征
⑴画一个三棱柱、四棱柱、五棱柱
由此可得棱柱的结构特征是:
⑵画一个三棱锥、四棱锥、五棱锥
由此可得棱锥的结构特征是:
⑶画一个三棱台、四棱台、五棱台
由此可得棱台的结构特征是:
画一个正四面体、正六面体以及正六面体各面中心连线构成的几何体(说明该几何体是什么几何体?)
⑷画一个圆柱及它的侧面展开图
圆柱的结构特征是
⑸画一个圆锥及它的侧面展开图
圆锥的结构特征是
⑹画一个圆台及它的侧面展开图
圆台的结构特征是
⑺画一个球
球的结构特征是
2.三视图与直观图
(1)把光由一点向外散射形成的投影,叫做
;
在一束平行光照射下形成的投影,叫做
.在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影。
(2)空间几何体的三视图:
。
画三视图的基本要求
高度一样,
长度一样,
宽度一样。
(3)斜二测画法的规则
①在已知图中建立直角坐标系xOy,画直观图时,它们分别对应x′轴和y′轴,两轴交于点O′,使∠x′O′y′=45°(或135°),它们确定的平面表示水平面。
②已知图形中平行于x轴或y轴的线段在直观图中分别画成
。
③已知图形中平行于x轴的线段的长度,在直观图中
;平行于y轴的线段的长度,在直观图中,长度为
。
【应用点】
1.⑴某几何体的直观图如图所示,画出该几何体的三视图.
⑵已知一几何体ABCD—A′B′C′D′的正视图、侧视图和俯视图分别为图中的①②③所示.图①中的四边形DCC′D′是面积为80的矩形;图②中的四边形ABCD是一直角梯形,AB=2AD且BC=CD;且原图中CC′=2BC.
请画出该几何体的直观图。
2.⑴如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的体积为
。
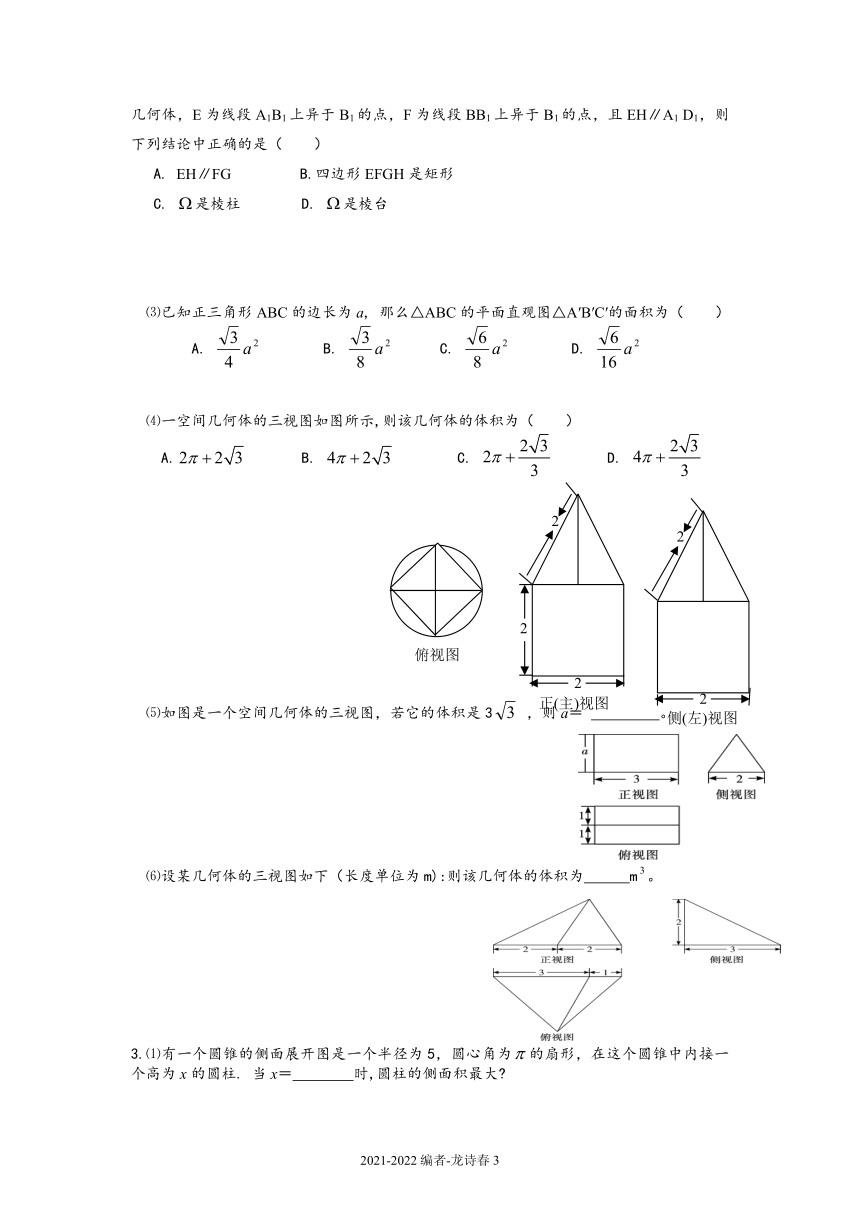
⑵(多选题)是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1
D1,则下列结论中正确的是(
)
A.
EH∥FG
B.四边形EFGH是矩形
C.
是棱柱
D.
是棱台
⑶已知正三角形ABC的边长为a,
那么△ABC的平面直观图△A′B′C′的面积为(
)
A.
B.
C.
D.
⑷一空间几何体的三视图如图所示,则该几何体的体积为(
)
A.
B.
C.
D.
⑸如图是一个空间几何体的三视图,若它的体积是3
,则a=
。
⑹设某几何体的三视图如下(长度单位为m):则该几何体的体积为
m。
3.⑴有一个圆锥的侧面展开图是一个半径为5,圆心角为的扇形,在这个圆锥中内接一个高为x的圆柱.
当x=
时,圆柱的侧面积最大?
⑵侧棱长为2a的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为(
)
A.6a
B.
4a
C.
2a
D.12a
⑶已知一圆锥底面圆的直径和母线长均为3,在该圆锥内放一个棱长为a的正四面体,并且正四面体可以在该圆锥内任意转动,则a的最大值是(
)
A.1
B.
C.
D.2
⑷(多选题)棱长为1的正方体ABCD-A1B1C1D1中,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是(
)
A.当0B.当CQ=时,S为等腰梯形
C.当D.当CQ=1时,S的面积为
⑸在四棱锥P-ABCD中,底面ABCD是矩形,侧棱AP⊥平面ABCD,AB=1,AP=,点M在线段BC上,且AM⊥MD,则当△PMD面积最小时,线段BC的长度为(
)
A.
B.
3
C.
D.2
⑹棱长均为2的正三棱柱ABC-A1B1C1中,E、F分别为棱BB1、A1C1的中点,若过A、E、F作一截面,则截面的周长为(
)
A.2+
B.
2+
C.2+
D.2+
3.⑴一个正方体内接于高为40
cm,底面半径为30
cm的圆锥中,求正方体的棱长。
⑵有一根长为3π
cm,底面半径为1
cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少?
【核心点】
1.画图、识图
2.多面体、旋转体的结构特征,三视图
11.2
空间几何体的表面积与体积
【知识点】
1.体积指的是
。面积指的是
。
柱体体积:
;锥体体积:
;台体体积:
;球体体积:
。
2.几何体的表面积指的是:
。
多面体的表面积
;圆柱侧面积:
;
圆锥侧面积:
;圆台侧面积:
;
球的表面积:
。
【应用点】
1.⑴用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为(
)
A.
B.
C.8
D.
⑵已知一个球与一个正三棱柱的三个侧面和两个底面相切,若这个球的体积是,则这个三棱柱的体积是(
)
A.
96
B.16
C.24
D.48
⑶直三棱柱ABC—A1B1C1的各顶点都在同一球面上.
若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于
。
⑷如图,棱长为2的正方体ABCD-A1B1C1D1中,E、F是线段B1D1上的动点,且EF=1,则几何体EABF的体积为
。
⑸棱长为1的正方体ABCD-A1B1C1D1中,ACB1D1与BDA1C1公共部分的体积为
。
⑹如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是
。
2.⑴一球与边长为2的正方体的各棱相切,则球的表面积是
,体积是
。
⑵已知圆台的上、下底面半径分别为r,R(r<R),一个平行于底面的截面将圆台的侧面分成面积相等的两部分,则这个截面圆的面积是
。
⑶如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,则该几何体的表面积(其中∠BAC=30°)是
。
⑷如图所示,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点,当底面ABC水平放置时,液面高为
。
⑸如图,边长为1的正方形网格中粗线画出的是某几何体的三视图,则该几何体的体积为
。
正方体的8个顶点中,有4个恰是正四面体的顶点,
则正方体与正四面体的表面积之比为________.
【核心点】
1.画图、识图
2.面积、体积计算
11.3
平面的基本性质、等角定理
【知识点】
1.平面的基本性质
自然语言
符号语言
图语言形
公理1
公理2
推论1
推论2
推论3
公理3
公理4
2.等角定理:空间中,两个角的对应边所在直线互相
,则这两个角
或
。
【应用点】
1.⑴已知E、F、G、H是空间中的四个点,设命题M:点E、F、G、H不共面;命题N:直线EF和GH不相交。那么M是N的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑵过正方体ABCD-A1B1C1D1的顶点A作直线L,使L与棱AB,AD,AA1所成的角都相等,这样的直线L可以作(
)
A.1条
B.2条
C.3条
D.4条
⑶(多选题)以下命题中为真命题的有(
)
A.点A、B、C∈直线a,A、B∈平面α,则C∈平面α
B.点A∈直线a,a平面α,则Aα
C.三条直线两两相交,则这三条直线共面
D.空间有四点不共面,则这四点中无三点共线
⑷平面六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3
B.4
C.5
D.6
⑸(多选题)设A、B、C、D是空间四个不同的点,下列命题中正确的是( )
A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD=BC
D.若AB=AC,DB=DC,则ADBC
⑹(多选题)在长方体中,D,E,F分别为所在棱的中点或体对角线的中点,则∠DEF=∠BAC的图形是(
)
A
B
C
D
2.如图,四面体A-BCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.判断直线EF、GH、BD是否相交于一点,并证明您的判断。
3.在长方体ABCDA1B1C1D1中
⑴如图,E是△BDC1的重心,判断A1、E、C三点是否共线,并证明您的判断;
⑵如图,E、F、G、H分别是所在棱的中点,判断E、F、G、H四点是否共面。并证明您的结论;
⑶如图,E、F、G、H分别是所在棱的中点,判断E、F、G、H四点是否共面。并证明您的结论;
【核心点】
1.画图、识图,
2.四个公理、三个推论、一个定理
11.4
直线与直线、直线与平面、平面与平面的位置关系
【知识点】
1.空间中两条直线的位置关系
自然语言
符号语言
图形语言
共面直线
相交
异面直线
2.空间中直线与平面的位置关系
自然语言
符号语言
图形语言
直线在平面内
直线在平面外
相交
3.空间中两个平面的位置关系
自然语言
符号语言
图形语言
相交
平行
【应用点】
1.⑴给出下列命题:
①若平面α上的直线a与平面β上的直线b为异面直线,直线c是α与β的交线,那么c至多与a、b中的一条相交;
②若直线a与b异面,直线b与c异面,则直线a与c异面;
③一定存在平面α同时和异面直线a、b都平行.
其中正确的命题为(
)
A.①
B.②
C.③
D.①③
⑵平面的斜线AB交于点B,过定点A的动直线与AB垂直,且交于点C,则动点C的轨迹是( )
A.一条直线
B.一个圆
C.一个椭圆
D.双曲线的一支
⑶已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是( )
A.平面ABC必平行于α
B.平面ABC必与α相交
C.平面ABC必不垂直于α
D.存在△ABC的一条中位线平行于α或在α内
⑷已知一条直线a和一个平面α,则在平面α内一定存在一条直线与直线a(
)
A.相交
B.平行
C.异面
D.垂直
⑸若P是两条异面直线外的任意一点,则( )
A.过点P有且仅有一条直线与都平行
B.过点P有且仅有一条直线与都垂直
C.过点P有且仅有一条直线与都相交
D.过点P有且仅有一条直线与都异面
⑹在正方体ABCDA1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线(
)
A.不存在
B.有且只有两条
C.有且只有三条
D.有无数条
2.⑴
对于平面和共面的直线m、n,下列命题中真命题是(
)
A.若m⊥,m⊥n,则n∥
B.若m∥,n∥,则m∥n
C.若m,n∥,则m∥n
D.若m、n与所成的角相等,则n∥m
⑵对于不重合的两个平面,给定下列条件:
①存在直线,使;
②存在平面使;
③内有不共线三点到的距离相等;
④存在异面直线,使∥,∥,∥,∥。
其中可以判定∥的有(
)个
A.
1
B.
2
C.
3
D.
4
⑶平面外有两条直线和,若和在平面内的射影分别是和,给出下列四个命题:
①;
②;
③与相交与相交或重合;
④与平行与平行或重合.
其中不正确的命题个数是(
)
A.1
B.2
C.3
D.4
⑷二面角,直线,,且与不垂直,与不垂直,那么(
)
A.与可能垂直,但不可能平行
B.与可能垂直,也可能平行
C.
与不可能垂直,但可能平行
D.
与不可能垂直,也不可能平行
【核心点】
1.画图、识图;
2.空间中,直线与直线、直线与平面、平面与平面的位置关系
11.6
直线、平面的平行关系
【知识点】
1.直线与直线平行的判定
①平行于同一条直线的两条直线平行。符号表示:
;图形表示:
②如果一条直线与一个平面平行,那么经过该直线的任何一个平面与此平面的交线和该直线平行。符号表示:
;图形表示:
③如果两个平行平面同时和第三个平面相交,那么它们的交线互相平行。
符号表示:
;图形表示:
④垂直于同一个平面的两条直线平行。
符号表示:
;图形表示:
⑤两条不重合直线的方向向量共线,则这两条直线平行。
符号表示:
;图形表示:
2.直线与平面平行的判定
①如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
符号表示:
;图形表示:
②如果两个平面平行,那么其中一个平面内的任意一条直线都平行于另一平面。
符号表示:
;图形表示:
③如果平面外一条直线的方向向量与该平面的法向量垂直,那么这条直线与这个平面平行。
符号表示:
;图形表示:
④如果平面外一条直线的方向向量与该平面内的两个不共线向量共面,那么这条直线与这个平面平行。
符号表示:
;图形表示:
3.平面与平面平行的判定
①如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行。
符号表示:
;图形表示:
②如果一个平面内的两条相交直线与另一个平面内的两条直线分别平行,那么这两个平面平行。
符号表示:
;图形表示:
③垂直于同一条直线的两个平面平行。
符号表示:
;图形表示:
④如果两个不重合平面的法向量共线,那么这两个平面平行。
符号表示:
;图形表示:
4.判断平行的方法:①几何法:线线平行线面平行面面平行;②向量法。
总的思路:由结论想判断方法,由条件想相关性质。
【应用点】
1.⑴过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )
A.4条
B.6条
C.8条
D.12条
⑵平面平面的一个充分条件是( )
A.存在一条直线
B.存在一条直线
C.存在两条平行直线
D.存在两条异面直线
⑶下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是(
)
A.
①、③
B.
①、④
C.
②、③
D.
②、④
⑷已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若mα,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是(
)
A.0
B.1
C.2
D.3
⑸m,n表示不同的直线,表示不同的平面,且,则“”是“(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
2.已知平面∩平面=,m∥,m∥,求证:m∥。
3.⑴设a、b为异面直线,为平面,若a⊥b,a⊥,b,求证:b∥。
⑵在斜三棱柱ABC-A1B1C1中,底面△ABC的重心为G点,E是线段BC1上一点,且BE=BC1,求证:GE∥侧面AA1B1B。
⑶如图,在四棱锥P-ABCD中,△PAD是边长为2的等边三角形,△ABC为等腰三角形,AB⊥BC,AC=1,∠DAC=90°,平面PAD⊥平面ABCD,棱PD上是否存在一点E,使得AE∥平面PBC?若存在,求出的值;若不存在,请说明理由。
4.⑴在正方体ABCD-A1B1C1D1中,M、N、P分别为AD1、BD、B1C上的点,且AM=BN=B1P,求证:平面MNP∥平面CC1D1D。
⑵设a、b为异面直线,、为平面,若a,b,a∥,b∥,求证:∥。
【核心点】
1.画图、识图;
2.空间中平行的判断与证明
11.7
直线、平面的垂直关系
【知识点】
1.直线与直线垂直的判定
①对于同一平面上的图形而言,平面几何中的垂直有关判定结论。
②一条直线垂直于一个平面,那么这条直线垂直于这个平面内的任意一条直线。
符号表示:
;图形表示:
③平面内的一条直线如果与平面的一条斜线在该平面内的射影垂直,则这条直线与斜线垂直。反之也成立。(三垂线定理及其逆定理)
符号表示:
;图形表示:
④如果两条直线的方向向量垂直,则这两条直线垂直。
符号表示:
;图形表示:
2.直线与平面垂直的判定结论:
①如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直。
符号表示:
;图形表示:
②如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直。
符号表示:
;图形表示:
③两平行直线中有一条与一个平面垂直,那么另一条也与这个平面垂直。
符号表示:
;图形表示:
④如果一条直线的方向向量与一个平面的法向量共线,那么这条直线与这个平面垂直。
符号表示:
;图形表示:
⑤如果一条直线的方向向量与一个平面内的两个不共线向量都垂直,那么这条直线与这个平面垂直。
符号表示:
;图形表示:
3.平面与平面垂直的判定结论:
①如果两个平面相交成的二面角是直二面角,则这两个平面互相垂直。
符号表示:
;图形表示:
②如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直。
符号表示:
;图形表示:
③如果两个平面的法向量互相垂直,那么这两个平面互相垂直。
符号表示:
;图形表示:
4.判断垂直的方法:①几何法:线线垂直线面垂直面面垂直;②向量法。
总的思路:由结论想判断方法,由条件想相关性质。
【应用点】
1.⑴若P是平面外一点,则下列命题正确的是(
)
A.过P只能作一条直线与平面相交
B.过P可作无数条直线与平面垂直
C.过P只能作一条直线与平面平行
D.过P可作无数条直线与平面平行
⑵设均为直线,其中在平面内,则“”是“且”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑶正方体ABCD—A1B1C1D1的棱上到异面直线AB,CC1的距离相等的点的个数为(
)
A.2
B.3
C.
4
D.
5
⑷设、是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是(
)
A.
B.
C.
D.
⑸若为一条直线,为三个互不重合的平面,给出下面三个命题:
①;②;③.
其中正确的命题有(
)
A.0个
B.1个
C.2个
D.3个
⑹(多选题)如图,三棱锥A—BCD中,AB⊥平面BCD,BD⊥CD,则下列结论正确的有(
)
A.平面ABC⊥平面ABD
B.平面ABC⊥平面ACD
C.平面ACD⊥平面ABD
D.平面BCD⊥平面ABD
⑺如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是
。
2.⑴如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD。
(I)求证:PA⊥BD
;(II)求证:平面PAD⊥平面PAB。
⑵在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(I)若D是BC的中点,求证:AD⊥CC1;
(II)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(III)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请说明判断的理由。
3.⑴已知:平面α⊥平面γ,平面β⊥平面γ,α∩β=l,求证:l⊥γ.
⑵如图,已知平行六面体ABCD-A1B1C1D1的底面是菱形,且∠C1CB=∠C1CD=∠BCD。
(I)求证:C1C⊥BD;
(II)当的值为多少时,能使A1C⊥平面C1BD?请给出证明。
【核心点】
1.画图、识图;
2.空间中,垂直的判断与证明
11.8
两异面直线成的角
【知识点】
1.图示两异面直线所成的角的意义:
⑴两异面直线a、b所成的角为90°a⊥b;
⑵两异面直线a、b所成的角的范围是
。
2.两异面直线a、b所成的角的求法:
⑴平移法:
。
⑵向量法:两异面直线a、b的方向向量分别为、,所成的角为,则
cos=|cos<,>|=
=
。
【应用点】
1.⑴如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点。那么异面直线OE和FD1所成的角的余弦值等于(
)
A.
B.
C.
D.
⑵已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影为BC的中点,则异面直线AB与CC1所成的角的余弦值为(
)
A.
B.
C.
D.
⑶正方体ABCD-A1B1C1D1中,M为AD1的中点,N为B1C的中点,则异面直线CM与D1N的夹角的余弦值是(
)
A.
B.
C.
D.前三个答案都不对
2.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,求异面直线PB与CD所成角的正弦值。
3.如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC,求异面直线AB和PC所成角的大小。
4.如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
⑴求证:PB∥面EFG;
⑵求异面直线EG与BD所成的角。
5.如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上。
⑴求证:平面COD⊥平面AOB;
⑵当D为AB的中点时,求异面直线AO与CD所成角的正切值。
【核心点】
1.画图、识图;
2.两条异面直线所成的角的求法:几何法、代数法。
11.9
直线与平面所的角
【知识点】
1.图示直线与平面所成的角
⑴直线与平面所成的角的范围是
;
⑵直线与平面垂直直线与平面成的角=
。
2.斜线与平面所成的角的求法:
①几何法:作角(由斜线上异于斜足的点向平面作垂线,得到斜线在平面上的射影)→证明(证明所作的符合线面角定义)→求角(构建直角三角形求之)。
②几何法:求出斜线上异于斜足的某点到斜足的距离d→求出该点到平面的距离h(等体积法、向量法等)→sin=。
③向量法:求斜线的一个方向向量→求平面的一个法向量→sin=|cos<,>|。
【应用点】
1.⑴如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60?,O为球心,则直线OA与截面ABC所成的角的余弦值是(
)
A.
B.
C.
D.
⑵把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为(
)
A.90°
B.60°
C.45°
D.30°
⑶设直线平面,过平面外一点A与都成30°角的直线有且只有(
)
A.1条
B.2条
C.3条
D.4条
⑷已知直线与平面成45°角,直线,若直线在内的射影与直线也成45°角,则与所成的角是(
)
A.30°
B.45°
C.60°
D.90°
⑸若一条直线与一个正四棱柱各个面所成的角都为,则=______。
2.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,求AB1与底面ABC所成角的正弦值。
3.如图,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点,求直线PC与平面PDE所成的角。
4.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m。
⑴试确定m,使直线AP与平面BDD1B1所成角的正切值为3;
⑵在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论。
5.如图,在正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,求A1B与平面BDE所成角的正弦值。
【核心点】
1.画图、识图;
2.平面的斜线与平面所成的角的求法:几何法、代数法。
11.10
二面角
【知识点】
1.二面角:从一条直线出发的两个半平面构成的图形。这条直线称为二面角的棱,两个半平面称为二面角的面。记为:-m-。
⑴图形表示二面角
⑵二面角的范围
。
2.二面角的平面角:二面角棱上任取一点,过这一点分别在两个半平面内
于棱的射线构成的角,图形表示如下
二面角的大小
二面角的平面角的大小。
3.二面角的求法:
①几何法:作二面角的平面角(垂面法,三垂线法。平面角的两边应在二面角两个面内且都与二面角的棱垂直)→证明(证明所作的角符合平面角定义)→求角(构建三角形求之)。
②向量法:求二面角的两个面的法向量,(设法向量坐标→通过法向量与平面上两个不共线向量的数量积为0列方程组→解方程组)→计算cos<,>→利用坐标系判断二面角是锐角还是钝角→二面角=<,>,或者二面角=-<,>
。
③面积法:作(找)出二面角的一个面上的特殊图形(如三角形)(称之为斜面)在另一个面上的射影面(称之为射影面)——求出斜面面积S斜与射影面的面积S射——cos<锐二面角>=S射/S斜。
【应用点】
1.⑴在正三棱柱ABC-A1B1C1中,D为AC的中点,AB1⊥BC1,则二面角D-BC1-C的大小为(
)
A.45°
B.60°
C.90°
D.135°
⑵已知平面α与β所成的二面角为80°,P为α、β外一定点,过点P的一条直线与α、β所成的角都是30°,则这样的直线有且仅有(
)
A.1条
B.2条
C.3条
D.4条
⑶二面角为,直线,直线,则直线与所成的角取值范围是(
)
A.
B.
C.
D.
2.如图,在直三棱柱ABC-A1B1C1中,AB=BC,D为BB1的中点。设AA1=AC=AB,求二面角A1-AD-C1的大小。
3.如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点。若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值。
4.四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2。求平面PAD和平面PBE所成二面角(锐角)的大小。
5.如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,∠BCF=∠CEF=90°,AD=,EF=2。当AB的长为何值时,二面角A-EF-C的大小为60°?
6.如图,在几何体P-ABCD中,面ABCD为矩形,PA⊥面ABCD,AB=PA=2,当≤AD≤时,求二面角B-PD-C的取值范围。
【核心点】
1.画图、识图;
2.二面角的求法:几何法、代数法。
11.11
距离
【知识点】
1.⑴点点间距离:
⑵点到直线的距离:
⑶点到平面的距离:
2.⑴两条平行直线间距离:
⑵两条异面直线间的距离:
⑶一条直线与一个平面平行,这条直线与这个平面间的距离:
3.两个平行平面间的距离:
【应用点】
1.⑴某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长棱的棱长是( )
A.
B.
C.
D.3
⑵已知二面角α-l-β为60°,动点P、Q分别在α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为(
)
A.
B.1
C.
D.2
⑶正方体ABCD?A1B1C1D1的棱长为2,点M为CC1的中点,点N为线段DD1上靠近D1的三等分点,平面BMN交AA1于点Q,则线段AQ的长为( )
A.
B.
C.
D.
⑷用六个完全相同的正方形围成的立体图形叫正六面体。已知正六面体ABCD-A1B1C1D1的棱长为4,则平面AB1D1与平面BC1D间的距离为(
)
A.
B.
C.
D.2
⑸在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=1,则点B到平面D1AC的距离等于________.
2.如图,已知四棱锥P?ABCD,底面ABCD为正方形,且PA⊥底面ABCD,过AB的平面ABFE与侧面PCD的交线为EF,且满足S△PEF∶S四边形CDEF=1∶3.
(1)证明:PB∥平面ACE;
(2)当PA=2AD=2时,求点F到平面ACE的距离.
3.如图,多面体ABCD-A1B1C1D1中,AA1、BB1、CC1、DD1均垂直于平面ABCD,AD∥BC,AB=BC=CD=AA1=CC1=2,BB1=1,AD=DD1=4。
⑴求直线AC与平面A1B1C1的距离;
⑵求直线BC1与平面A1B1C1所成角的正切值。
4.正方体ABCD?A1B1C1D1的棱长为2,点E为B1C1的中点.
⑴求证平面BDE与平面A1B1C1D1的交线过C1D1的中点;
⑵求点C1到平面BDE的距离。
【核心点】
1.画图、识图;
2.两个平行平面间的距离,直线与平面间的距离→点到平面的距离;直线与直线的距离、点到直线的距离→点点间的距离。
11.12
体积
【知识点】
柱体体积:
锥体体积:
台体体积:
球体体积:
【应用点】
1.⑴设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D?ABC体积的最大值为( )
A.12 B.18
C.24
D.54
⑵在棱长为1的正方体ABCD?A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F将点B1所在的几何体削去,则剩余几何体的体积为( )
A.
B.
C.
D.
⑶已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________.
⑷已知三棱锥S?ABC的顶点都在球O的球面上,△ABC是边长为3的正三角形,SC为球O的直径,且SC=4,则此三棱锥的体积为________.
⑸如图,圆形纸片的圆心为O,半径为5
cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为________.
2.在四面体P?ABC中,AB=BC=2,∠ABC=120°,PA=PB=PC=4,求四面体P?ABC的体积.
3.在四面体ABCD中,若有5条棱长均为3,只有一条棱长为4,求此四面体的体积.
4.在四面体D?ABC中,三组对棱分别相等,且依次为2,2,2,求此四面体的体积.
5.三棱锥的三条侧棱两两垂直,3个侧面与底面所成的角分别为30°,45°,60°,底面面积为,求三棱锥的体积.
6.如图多面体ABCDEF中,四边形ABCD是边长为2的菱形,∠DAB=60°.EF∥AC,EA=ED=EF=.
(1)求AD与BE所成的角;
(2)若BE=,求三棱锥B?CDF的体积.
【核心点】
1.画图、识图;
2.体积的求法:直接法、分割法、补形法。
11.13
球
【知识点】
1.球的截口是一个圆,该圆半径的平方=球的半径的平方-
的平方
2.球心的确定:
多面体的外接球球心到多面体各顶点距离相等,内切球球心到多面体各面的距离相等。
⑴正方体的外接球、内切球球心均是体对角线的
;长方体的外接球球心是体对角线的
,长方体不一定有内切球;
⑵正棱柱的外接球球心是上下底面中心的连线的
,正棱柱不一定有内切球;
⑶直三棱柱的外接球球心是上下底面的
心的连线的
,但不一定有内切球;
⑷正棱锥的外接球、内切球球心都在该棱锥的
上;
⑸若多面体中有三条共点且两两互相垂直的线段,可借助这三条线段构建长方体确定球心;
⑹通过构建三角形找球心
3.研究透彻六个球:正方体的外接球、棱切球、内切球,正四面体的外接球、棱切球、内切球。
【应用点】
1.⑴已知球O与棱长为4的正四面体的各棱相切,则球O的体积为( )
A.π B.π
C.π
D.π
⑵如图,一个三棱锥的三视图均为直角三角形.若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )
A.4π
B.16π
C.24π
D.25π
⑶把一个皮球放入如图所示的由8根长均为20
cm的铁丝接成的四棱锥形骨架中,使皮球的表面与8根铁丝都有接触点(皮球不变形),则皮球的半径为( )
A.10
cm
B.10
cm
C.10
cm
D.30
cm
⑷三棱锥P?ABC的四个顶点都在体积为的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
A.4
B.6
C.8
D.10
⑸已知圆柱的高为2,底面半径为,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于( )
A.4π
B.π
C.π
D.16π
⑹已知底面半径为1,高为的圆锥的顶点和底面圆周都在球O的球面上,则球O的表面积为( )
A.
B.4π
C.
D.12π
2.⑴已知三棱柱A1B1C1?ABC内接于球O,AB=AC=24,∠BAC=120°,AA1⊥平面ABC,AA1=14,则球O的表面积是________.
⑵在三棱锥V?ABC的四个面中,有两个面都是直角边为1的等腰直角三角形,另两个面都是直角边分别为1和的直角三角形,则该三棱锥的外接球的体积为________.
⑶在正四棱锥P-ABCD中,底面ABCD是边长为4的正方形,E、F分别是AB、CD的中点,cos∠PEF=,若A、B、C、D、P在同一球面上,则此球的体积为
。
⑷三棱台ABC-A1B1C1中,A1A=B1B=C1C=A1B1=2,AB=4,侧面A1B1BA⊥底面ABC,则该三棱台的外接球的表面积是
。
【核心点】
1.画图、识图;
2.解与球相关的组合体问题的策略:
(1)过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题.
(2)利用平面几何知识寻找几何体中元素间的关系,或通过画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
11.14
折叠问题
【应用点】
1.⑴已知矩形ABCD,AB=4,AD=2,E为AB的中点,沿直线DE将△ADE翻折成△PDE,直线PB与平面BCDE所成角最大时PB的长是(
)
A.
B.
C.
D.
⑵已知C为Rt△ABD斜边BD上一点,且△ACD为正三角形,将△ABC沿AC翻折到△AB/C,若在三棱锥B/—ACD中,直线CB/、AB/与平面ACD所成的角分别为α、β,则(
)
A.0<α<β
B.β<α≤2β
C.2β≤α≤3β
D.3β≤α
⑶在矩形ABCD中,AB=2,BC=1,E、N分别为边AB、BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为A1D、A1C的中点,则在△ADE折起的过程中(
)
A.DE可以与A1C垂直
B.不可能同时做到MN∥平面A1BE且BK∥平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.
直线A1E、BK与平面BCDE所成的角能够同时取得最大值
⑷(多选题)如图,在正方形ABCD中,AC为对角线,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H.下列说法错误的是(
)
A.AG⊥△EFH所在平面
B.AH⊥△EFH所在平面
C.HF⊥△AEF所在平面
D.HG⊥△AEF所在平面
⑸如图,在矩形ABCD中,2AB=BC=2,AE=CF=1,将A、C分别沿BE、DF向上翻折至A/、C/,则A/C/取最小值时,二面角A/-EF-C/的余弦值是
。
2.如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
3.如图①,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图②所示的四棱锥D1?ABCE,其中平面D1AE⊥平面ABCE.
(1)设F为CD1的中点,试在AB上找一点M,使得MF∥平面D1AE;
(2)求直线BD1与平面CD1E所成的角的正弦值.
4.已知直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AD=,AB=1,如图①所示,将△ABD沿BD折起到△PBD的位置得三棱锥P?BCD,如图②所示.
(1)求证:BD⊥PC;
(2)当平面PBD⊥平面PBC时,求二面角P?DC?B的大小.
【核心点】
1.画图、识图;
2.注意折叠前后变化的量与不变化的量。
11.15
存在性问题
【应用点】
1.如图,在四棱锥P?ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.
(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M?AC?D的大小为45°?若存在,求BM与平面MAC所成角的正弦值;若不存在,请说明理由.
2.如图,在四棱锥E?ABCD中,底面ABCD为直角梯形,其中CD∥AB,BC⊥AB,侧面ABE⊥平面ABCD,且AB=AE=BE=2BC=2CD=2,动点F在棱AE,且EF=λFA.
(1)试探究λ的值,使CE∥平面BDF,并给予证明;
(2)当λ=1时,求直线CE与平面BDF所成角的正弦值.
3.边长为4的正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点,现将△ABC沿CD翻折成直二面角A-DC-B。
⑴求二面角E-DF-C的余弦值;
⑵在线段BC上是否存在点P,使AP⊥DE?若存在,试指出点P的位置;若不存在,请说明理由。
4.在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,△PAD是边长为2的正三角形,PC=,E为线段AD的中点。
⑴求证:平面PBC⊥平面PBE;
⑵是否存在满足=(>0)的点F,使得VB-PAE=VD-PFB?若存在,则求出的值;若不存在,请说明理由。
5.棱柱ABCD?A1B1C1D1的所有棱长都等于2,平面AA1C1C⊥平面ABCD,∠ABC=∠A1AC=60°。
⑴求二面角D-A1A-C的余弦值;
⑵在直线CC1上是否存在点P,使得BP平面DA1C1?
若存在,求出点P的位置;若不存在,请说明理由。
6.四边形ABCD是圆柱OO1的轴截面,点P是底面圆周上异于A、B的一点,若圆柱的侧面积为2,体积为,点Q是DP上靠近点D的三等分点,是否存在点P,使得直线AQ与平面BDP所成的角正弦值最大?若存在,求出相应的正弦值,并指出点P的位置;若不存在,请说明理由。
7.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,M是线段EF的中点,AB=,AF=t。
⑴若t=1,求二面角A-DF-B的大小;
⑵若线段AC上总存在一点P,使得PF⊥BE,求t的最大值。
【核心点】
1.画图、识图;
2.解决问题的方法:几何法、向量法
11.16
截面、展开
【应用点】
1.已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )
A.
B.
C.
D.
2.侧棱长为2a的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为(
)
A.
2a
B.6a
C.4a
D.12a
3.在棱长均为2的正四面体ABCD中,M为AC的中点,E为AB的中点,P是DM上的动点,Q是平面ECD上的动点,则AP+PQ的最小值是(
)
A.
2
B.
C.+
D.
4.在正方体ABCD?A1B1C1D1中,平面α垂直于对角线AC且截正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则(
)
A.S为定值,l不为定值
B.S不为定值,l为定值
C.S、l均为定值
D.S、l均不为定值
5.(多选题)直三棱柱ABC-A1B1C1的所有棱长都是4,P、Q、R分别是AA1、AB、B1C1上的点,AP=AQ=2,B1R=3,过P、Q、R三点的平面将三棱柱分为两部分,下列说法正确的是(
)
A.截面是五边形
B.截面面积为3
C.截面将三棱柱体积平分
D.截面与底面所成锐二面角的大小为60°
6.过棱长为1的正方体的一条体对角线作截面,则截得正方体的截面面积的最小值是(
)
A.
1
B.
C.
D.
7.某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A.2
B.2
C.3
D.2
8.正四面体ABCD的外接球半径为2,过棱AB作该球的截面,则截面面积的最小值为________.
【核心点】
画图、识图;
11.17
综合问题
【知识点】
1.转化思想:空间问题平面化,几何问题向量化,几何问题代数化(建立空间坐标系)。
2.平行与垂直的证明:由条件想性质,由结论想判定。
3.空间三种角的求法:①几何法:作——证——求。②向量法。
4.距离求法:各种距离转化为两点间距离或点到平面的距离(等体积法)。
【应用点】
1.已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为。
⑴证明BF∥平面ADE;
⑵△ACD为正三角形,判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结
论,并求角的余弦值。
2.如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA、PB、AC的中点,AC=16,PA=PC=10。
⑴设G是OC的中点,证明:FG∥平面BOE;
⑵证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离。
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°.点D,E分别在棱PB,PC上,且DE∥BC.
⑴求证:BC⊥平面PAC;
⑵当D为PB的中点时,求AD与平面PAC所成的角的大小;
⑶是否存在点E使得二面角A-DE-P为直二面角?并说明理由。
4.四棱锥P?ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M?AB?D的余弦值.
5.如图,在四棱锥P?ABCD中,E,F分别是PC,PD的中点,底面ABCD是边长为2的正方形,PA=PD=2,且平面PAD⊥平面ABCD.
(1)求证:平面AEF⊥平面PCD;
(2)求平面AEF与平面ACE所成锐二面角的余弦值.
6.如图,三棱柱ABC?A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
(1)当为何值时,平面CDG⊥平面A1DE?
(2)求平面A1BF与平面A1DE所成的锐二面角的余弦值.
7.如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
(1)求证:AC⊥平面BDEF;
(2)求直线DH与平面BDEF所成角的正弦值;
(3)求二面角H?BD?C的大小.
8.如图,在四棱锥P?ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB.
(1)求证:BE∥平面PAD;
(2)若二面角P?CD?A的正切值为2,求直线PB与平面PCD所成角的正弦值.
9.如图,已知平行四边形ABCD与△EMN所在的平面都与矩形BDEF所在的平面垂直,且∠BAD=60°,AB=MN=2AD=2,EM=EN,F为MN的中点.
(1)求证:MN∥AD;
(2)若直线AE与平面ABCD所成的角为60°,求二面角M?AB?C的余弦值.
10.如图,在三棱锥P?ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M?PA?C为30°,求PC与平面PAM所成角的正弦值.
11.如图,在四棱锥P?ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD,E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P?AC?E的余弦值为,求直线PA与平面EAC所成角的正弦值.
12.如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1。
⑴证明AB=AC
;
⑵设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小。
13.在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2。以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N。
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;
(3)求点N到平面ACM的距离。
14.如图,四棱锥S—ABCD的底面是正方形,SD平面ABCD,SD=2a,AD=a,点E是SD上的点,且DE=a(0<≤2)。
⑴求证:对任意的0<≤2,都有AC⊥BE;
⑵设二面角C—AE—D的大小为,直线BE与平面ABCD所成的角为,若,求的值
。
15.如图,在五面体ABCDEF中,FA
平面ABCD,AD//BC//FE,ABAD,M为EC的中点,AF=AB=BC=FE=AD。
⑴求异面直线BF与DE所成的角的大小;
⑵证明平面AMD平面CDE;
⑶求二面角A-CD-E的余弦值。
【核心点】
识图、画图;
两种方法:几何法、向量法。2021-2022编者-龙诗春215
空间简单几何体的直观图、三视图
【知识点】
1.柱、锥、台、球的结构特征
⑴画一个三棱柱、四棱柱、五棱柱
由此可得棱柱的结构特征是:
⑵画一个三棱锥、四棱锥、五棱锥
由此可得棱锥的结构特征是:
⑶画一个三棱台、四棱台、五棱台
由此可得棱台的结构特征是:
画一个正四面体、正六面体以及正六面体各面中心连线构成的几何体(说明该几何体是什么几何体?)
⑷画一个圆柱及它的侧面展开图
圆柱的结构特征是
⑸画一个圆锥及它的侧面展开图
圆锥的结构特征是
⑹画一个圆台及它的侧面展开图
圆台的结构特征是
⑺画一个球
球的结构特征是
2.三视图与直观图
(1)把光由一点向外散射形成的投影,叫做
;
在一束平行光照射下形成的投影,叫做
.在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影。
(2)空间几何体的三视图:
。
画三视图的基本要求
高度一样,
长度一样,
宽度一样。
(3)斜二测画法的规则
①在已知图中建立直角坐标系xOy,画直观图时,它们分别对应x′轴和y′轴,两轴交于点O′,使∠x′O′y′=45°(或135°),它们确定的平面表示水平面。
②已知图形中平行于x轴或y轴的线段在直观图中分别画成
。
③已知图形中平行于x轴的线段的长度,在直观图中
;平行于y轴的线段的长度,在直观图中,长度为
。
【应用点】
1.⑴某几何体的直观图如图所示,画出该几何体的三视图.
⑵已知一几何体ABCD—A′B′C′D′的正视图、侧视图和俯视图分别为图中的①②③所示.图①中的四边形DCC′D′是面积为80的矩形;图②中的四边形ABCD是一直角梯形,AB=2AD且BC=CD;且原图中CC′=2BC.
请画出该几何体的直观图。
2.⑴如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的体积为
。
⑵(多选题)是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1
D1,则下列结论中正确的是(
)
A.
EH∥FG
B.四边形EFGH是矩形
C.
是棱柱
D.
是棱台
⑶已知正三角形ABC的边长为a,
那么△ABC的平面直观图△A′B′C′的面积为(
)
A.
B.
C.
D.
⑷一空间几何体的三视图如图所示,则该几何体的体积为(
)
A.
B.
C.
D.
⑸如图是一个空间几何体的三视图,若它的体积是3
,则a=
。
⑹设某几何体的三视图如下(长度单位为m):则该几何体的体积为
m。
3.⑴有一个圆锥的侧面展开图是一个半径为5,圆心角为的扇形,在这个圆锥中内接一个高为x的圆柱.
当x=
时,圆柱的侧面积最大?
⑵侧棱长为2a的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为(
)
A.6a
B.
4a
C.
2a
D.12a
⑶已知一圆锥底面圆的直径和母线长均为3,在该圆锥内放一个棱长为a的正四面体,并且正四面体可以在该圆锥内任意转动,则a的最大值是(
)
A.1
B.
C.
D.2
⑷(多选题)棱长为1的正方体ABCD-A1B1C1D1中,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是(
)
A.当0
C.当
⑸在四棱锥P-ABCD中,底面ABCD是矩形,侧棱AP⊥平面ABCD,AB=1,AP=,点M在线段BC上,且AM⊥MD,则当△PMD面积最小时,线段BC的长度为(
)
A.
B.
3
C.
D.2
⑹棱长均为2的正三棱柱ABC-A1B1C1中,E、F分别为棱BB1、A1C1的中点,若过A、E、F作一截面,则截面的周长为(
)
A.2+
B.
2+
C.2+
D.2+
3.⑴一个正方体内接于高为40
cm,底面半径为30
cm的圆锥中,求正方体的棱长。
⑵有一根长为3π
cm,底面半径为1
cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少?
【核心点】
1.画图、识图
2.多面体、旋转体的结构特征,三视图
11.2
空间几何体的表面积与体积
【知识点】
1.体积指的是
。面积指的是
。
柱体体积:
;锥体体积:
;台体体积:
;球体体积:
。
2.几何体的表面积指的是:
。
多面体的表面积
;圆柱侧面积:
;
圆锥侧面积:
;圆台侧面积:
;
球的表面积:
。
【应用点】
1.⑴用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为(
)
A.
B.
C.8
D.
⑵已知一个球与一个正三棱柱的三个侧面和两个底面相切,若这个球的体积是,则这个三棱柱的体积是(
)
A.
96
B.16
C.24
D.48
⑶直三棱柱ABC—A1B1C1的各顶点都在同一球面上.
若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于
。
⑷如图,棱长为2的正方体ABCD-A1B1C1D1中,E、F是线段B1D1上的动点,且EF=1,则几何体EABF的体积为
。
⑸棱长为1的正方体ABCD-A1B1C1D1中,ACB1D1与BDA1C1公共部分的体积为
。
⑹如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是
。
2.⑴一球与边长为2的正方体的各棱相切,则球的表面积是
,体积是
。
⑵已知圆台的上、下底面半径分别为r,R(r<R),一个平行于底面的截面将圆台的侧面分成面积相等的两部分,则这个截面圆的面积是
。
⑶如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,则该几何体的表面积(其中∠BAC=30°)是
。
⑷如图所示,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点,当底面ABC水平放置时,液面高为
。
⑸如图,边长为1的正方形网格中粗线画出的是某几何体的三视图,则该几何体的体积为
。
正方体的8个顶点中,有4个恰是正四面体的顶点,
则正方体与正四面体的表面积之比为________.
【核心点】
1.画图、识图
2.面积、体积计算
11.3
平面的基本性质、等角定理
【知识点】
1.平面的基本性质
自然语言
符号语言
图语言形
公理1
公理2
推论1
推论2
推论3
公理3
公理4
2.等角定理:空间中,两个角的对应边所在直线互相
,则这两个角
或
。
【应用点】
1.⑴已知E、F、G、H是空间中的四个点,设命题M:点E、F、G、H不共面;命题N:直线EF和GH不相交。那么M是N的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑵过正方体ABCD-A1B1C1D1的顶点A作直线L,使L与棱AB,AD,AA1所成的角都相等,这样的直线L可以作(
)
A.1条
B.2条
C.3条
D.4条
⑶(多选题)以下命题中为真命题的有(
)
A.点A、B、C∈直线a,A、B∈平面α,则C∈平面α
B.点A∈直线a,a平面α,则Aα
C.三条直线两两相交,则这三条直线共面
D.空间有四点不共面,则这四点中无三点共线
⑷平面六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3
B.4
C.5
D.6
⑸(多选题)设A、B、C、D是空间四个不同的点,下列命题中正确的是( )
A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD=BC
D.若AB=AC,DB=DC,则ADBC
⑹(多选题)在长方体中,D,E,F分别为所在棱的中点或体对角线的中点,则∠DEF=∠BAC的图形是(
)
A
B
C
D
2.如图,四面体A-BCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.判断直线EF、GH、BD是否相交于一点,并证明您的判断。
3.在长方体ABCDA1B1C1D1中
⑴如图,E是△BDC1的重心,判断A1、E、C三点是否共线,并证明您的判断;
⑵如图,E、F、G、H分别是所在棱的中点,判断E、F、G、H四点是否共面。并证明您的结论;
⑶如图,E、F、G、H分别是所在棱的中点,判断E、F、G、H四点是否共面。并证明您的结论;
【核心点】
1.画图、识图,
2.四个公理、三个推论、一个定理
11.4
直线与直线、直线与平面、平面与平面的位置关系
【知识点】
1.空间中两条直线的位置关系
自然语言
符号语言
图形语言
共面直线
相交
异面直线
2.空间中直线与平面的位置关系
自然语言
符号语言
图形语言
直线在平面内
直线在平面外
相交
3.空间中两个平面的位置关系
自然语言
符号语言
图形语言
相交
平行
【应用点】
1.⑴给出下列命题:
①若平面α上的直线a与平面β上的直线b为异面直线,直线c是α与β的交线,那么c至多与a、b中的一条相交;
②若直线a与b异面,直线b与c异面,则直线a与c异面;
③一定存在平面α同时和异面直线a、b都平行.
其中正确的命题为(
)
A.①
B.②
C.③
D.①③
⑵平面的斜线AB交于点B,过定点A的动直线与AB垂直,且交于点C,则动点C的轨迹是( )
A.一条直线
B.一个圆
C.一个椭圆
D.双曲线的一支
⑶已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是( )
A.平面ABC必平行于α
B.平面ABC必与α相交
C.平面ABC必不垂直于α
D.存在△ABC的一条中位线平行于α或在α内
⑷已知一条直线a和一个平面α,则在平面α内一定存在一条直线与直线a(
)
A.相交
B.平行
C.异面
D.垂直
⑸若P是两条异面直线外的任意一点,则( )
A.过点P有且仅有一条直线与都平行
B.过点P有且仅有一条直线与都垂直
C.过点P有且仅有一条直线与都相交
D.过点P有且仅有一条直线与都异面
⑹在正方体ABCDA1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线(
)
A.不存在
B.有且只有两条
C.有且只有三条
D.有无数条
2.⑴
对于平面和共面的直线m、n,下列命题中真命题是(
)
A.若m⊥,m⊥n,则n∥
B.若m∥,n∥,则m∥n
C.若m,n∥,则m∥n
D.若m、n与所成的角相等,则n∥m
⑵对于不重合的两个平面,给定下列条件:
①存在直线,使;
②存在平面使;
③内有不共线三点到的距离相等;
④存在异面直线,使∥,∥,∥,∥。
其中可以判定∥的有(
)个
A.
1
B.
2
C.
3
D.
4
⑶平面外有两条直线和,若和在平面内的射影分别是和,给出下列四个命题:
①;
②;
③与相交与相交或重合;
④与平行与平行或重合.
其中不正确的命题个数是(
)
A.1
B.2
C.3
D.4
⑷二面角,直线,,且与不垂直,与不垂直,那么(
)
A.与可能垂直,但不可能平行
B.与可能垂直,也可能平行
C.
与不可能垂直,但可能平行
D.
与不可能垂直,也不可能平行
【核心点】
1.画图、识图;
2.空间中,直线与直线、直线与平面、平面与平面的位置关系
11.6
直线、平面的平行关系
【知识点】
1.直线与直线平行的判定
①平行于同一条直线的两条直线平行。符号表示:
;图形表示:
②如果一条直线与一个平面平行,那么经过该直线的任何一个平面与此平面的交线和该直线平行。符号表示:
;图形表示:
③如果两个平行平面同时和第三个平面相交,那么它们的交线互相平行。
符号表示:
;图形表示:
④垂直于同一个平面的两条直线平行。
符号表示:
;图形表示:
⑤两条不重合直线的方向向量共线,则这两条直线平行。
符号表示:
;图形表示:
2.直线与平面平行的判定
①如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
符号表示:
;图形表示:
②如果两个平面平行,那么其中一个平面内的任意一条直线都平行于另一平面。
符号表示:
;图形表示:
③如果平面外一条直线的方向向量与该平面的法向量垂直,那么这条直线与这个平面平行。
符号表示:
;图形表示:
④如果平面外一条直线的方向向量与该平面内的两个不共线向量共面,那么这条直线与这个平面平行。
符号表示:
;图形表示:
3.平面与平面平行的判定
①如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行。
符号表示:
;图形表示:
②如果一个平面内的两条相交直线与另一个平面内的两条直线分别平行,那么这两个平面平行。
符号表示:
;图形表示:
③垂直于同一条直线的两个平面平行。
符号表示:
;图形表示:
④如果两个不重合平面的法向量共线,那么这两个平面平行。
符号表示:
;图形表示:
4.判断平行的方法:①几何法:线线平行线面平行面面平行;②向量法。
总的思路:由结论想判断方法,由条件想相关性质。
【应用点】
1.⑴过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )
A.4条
B.6条
C.8条
D.12条
⑵平面平面的一个充分条件是( )
A.存在一条直线
B.存在一条直线
C.存在两条平行直线
D.存在两条异面直线
⑶下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是(
)
A.
①、③
B.
①、④
C.
②、③
D.
②、④
⑷已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若mα,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是(
)
A.0
B.1
C.2
D.3
⑸m,n表示不同的直线,表示不同的平面,且,则“”是“(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
2.已知平面∩平面=,m∥,m∥,求证:m∥。
3.⑴设a、b为异面直线,为平面,若a⊥b,a⊥,b,求证:b∥。
⑵在斜三棱柱ABC-A1B1C1中,底面△ABC的重心为G点,E是线段BC1上一点,且BE=BC1,求证:GE∥侧面AA1B1B。
⑶如图,在四棱锥P-ABCD中,△PAD是边长为2的等边三角形,△ABC为等腰三角形,AB⊥BC,AC=1,∠DAC=90°,平面PAD⊥平面ABCD,棱PD上是否存在一点E,使得AE∥平面PBC?若存在,求出的值;若不存在,请说明理由。
4.⑴在正方体ABCD-A1B1C1D1中,M、N、P分别为AD1、BD、B1C上的点,且AM=BN=B1P,求证:平面MNP∥平面CC1D1D。
⑵设a、b为异面直线,、为平面,若a,b,a∥,b∥,求证:∥。
【核心点】
1.画图、识图;
2.空间中平行的判断与证明
11.7
直线、平面的垂直关系
【知识点】
1.直线与直线垂直的判定
①对于同一平面上的图形而言,平面几何中的垂直有关判定结论。
②一条直线垂直于一个平面,那么这条直线垂直于这个平面内的任意一条直线。
符号表示:
;图形表示:
③平面内的一条直线如果与平面的一条斜线在该平面内的射影垂直,则这条直线与斜线垂直。反之也成立。(三垂线定理及其逆定理)
符号表示:
;图形表示:
④如果两条直线的方向向量垂直,则这两条直线垂直。
符号表示:
;图形表示:
2.直线与平面垂直的判定结论:
①如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直。
符号表示:
;图形表示:
②如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直。
符号表示:
;图形表示:
③两平行直线中有一条与一个平面垂直,那么另一条也与这个平面垂直。
符号表示:
;图形表示:
④如果一条直线的方向向量与一个平面的法向量共线,那么这条直线与这个平面垂直。
符号表示:
;图形表示:
⑤如果一条直线的方向向量与一个平面内的两个不共线向量都垂直,那么这条直线与这个平面垂直。
符号表示:
;图形表示:
3.平面与平面垂直的判定结论:
①如果两个平面相交成的二面角是直二面角,则这两个平面互相垂直。
符号表示:
;图形表示:
②如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直。
符号表示:
;图形表示:
③如果两个平面的法向量互相垂直,那么这两个平面互相垂直。
符号表示:
;图形表示:
4.判断垂直的方法:①几何法:线线垂直线面垂直面面垂直;②向量法。
总的思路:由结论想判断方法,由条件想相关性质。
【应用点】
1.⑴若P是平面外一点,则下列命题正确的是(
)
A.过P只能作一条直线与平面相交
B.过P可作无数条直线与平面垂直
C.过P只能作一条直线与平面平行
D.过P可作无数条直线与平面平行
⑵设均为直线,其中在平面内,则“”是“且”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件
⑶正方体ABCD—A1B1C1D1的棱上到异面直线AB,CC1的距离相等的点的个数为(
)
A.2
B.3
C.
4
D.
5
⑷设、是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是(
)
A.
B.
C.
D.
⑸若为一条直线,为三个互不重合的平面,给出下面三个命题:
①;②;③.
其中正确的命题有(
)
A.0个
B.1个
C.2个
D.3个
⑹(多选题)如图,三棱锥A—BCD中,AB⊥平面BCD,BD⊥CD,则下列结论正确的有(
)
A.平面ABC⊥平面ABD
B.平面ABC⊥平面ACD
C.平面ACD⊥平面ABD
D.平面BCD⊥平面ABD
⑺如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是
。
2.⑴如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD。
(I)求证:PA⊥BD
;(II)求证:平面PAD⊥平面PAB。
⑵在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(I)若D是BC的中点,求证:AD⊥CC1;
(II)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(III)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请说明判断的理由。
3.⑴已知:平面α⊥平面γ,平面β⊥平面γ,α∩β=l,求证:l⊥γ.
⑵如图,已知平行六面体ABCD-A1B1C1D1的底面是菱形,且∠C1CB=∠C1CD=∠BCD。
(I)求证:C1C⊥BD;
(II)当的值为多少时,能使A1C⊥平面C1BD?请给出证明。
【核心点】
1.画图、识图;
2.空间中,垂直的判断与证明
11.8
两异面直线成的角
【知识点】
1.图示两异面直线所成的角的意义:
⑴两异面直线a、b所成的角为90°a⊥b;
⑵两异面直线a、b所成的角的范围是
。
2.两异面直线a、b所成的角的求法:
⑴平移法:
。
⑵向量法:两异面直线a、b的方向向量分别为、,所成的角为,则
cos=|cos<,>|=
=
。
【应用点】
1.⑴如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点。那么异面直线OE和FD1所成的角的余弦值等于(
)
A.
B.
C.
D.
⑵已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影为BC的中点,则异面直线AB与CC1所成的角的余弦值为(
)
A.
B.
C.
D.
⑶正方体ABCD-A1B1C1D1中,M为AD1的中点,N为B1C的中点,则异面直线CM与D1N的夹角的余弦值是(
)
A.
B.
C.
D.前三个答案都不对
2.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,求异面直线PB与CD所成角的正弦值。
3.如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC,求异面直线AB和PC所成角的大小。
4.如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
⑴求证:PB∥面EFG;
⑵求异面直线EG与BD所成的角。
5.如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上。
⑴求证:平面COD⊥平面AOB;
⑵当D为AB的中点时,求异面直线AO与CD所成角的正切值。
【核心点】
1.画图、识图;
2.两条异面直线所成的角的求法:几何法、代数法。
11.9
直线与平面所的角
【知识点】
1.图示直线与平面所成的角
⑴直线与平面所成的角的范围是
;
⑵直线与平面垂直直线与平面成的角=
。
2.斜线与平面所成的角的求法:
①几何法:作角(由斜线上异于斜足的点向平面作垂线,得到斜线在平面上的射影)→证明(证明所作的符合线面角定义)→求角(构建直角三角形求之)。
②几何法:求出斜线上异于斜足的某点到斜足的距离d→求出该点到平面的距离h(等体积法、向量法等)→sin=。
③向量法:求斜线的一个方向向量→求平面的一个法向量→sin=|cos<,>|。
【应用点】
1.⑴如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60?,O为球心,则直线OA与截面ABC所成的角的余弦值是(
)
A.
B.
C.
D.
⑵把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为(
)
A.90°
B.60°
C.45°
D.30°
⑶设直线平面,过平面外一点A与都成30°角的直线有且只有(
)
A.1条
B.2条
C.3条
D.4条
⑷已知直线与平面成45°角,直线,若直线在内的射影与直线也成45°角,则与所成的角是(
)
A.30°
B.45°
C.60°
D.90°
⑸若一条直线与一个正四棱柱各个面所成的角都为,则=______。
2.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,求AB1与底面ABC所成角的正弦值。
3.如图,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点,求直线PC与平面PDE所成的角。
4.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m。
⑴试确定m,使直线AP与平面BDD1B1所成角的正切值为3;
⑵在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论。
5.如图,在正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,求A1B与平面BDE所成角的正弦值。
【核心点】
1.画图、识图;
2.平面的斜线与平面所成的角的求法:几何法、代数法。
11.10
二面角
【知识点】
1.二面角:从一条直线出发的两个半平面构成的图形。这条直线称为二面角的棱,两个半平面称为二面角的面。记为:-m-。
⑴图形表示二面角
⑵二面角的范围
。
2.二面角的平面角:二面角棱上任取一点,过这一点分别在两个半平面内
于棱的射线构成的角,图形表示如下
二面角的大小
二面角的平面角的大小。
3.二面角的求法:
①几何法:作二面角的平面角(垂面法,三垂线法。平面角的两边应在二面角两个面内且都与二面角的棱垂直)→证明(证明所作的角符合平面角定义)→求角(构建三角形求之)。
②向量法:求二面角的两个面的法向量,(设法向量坐标→通过法向量与平面上两个不共线向量的数量积为0列方程组→解方程组)→计算cos<,>→利用坐标系判断二面角是锐角还是钝角→二面角=<,>,或者二面角=-<,>
。
③面积法:作(找)出二面角的一个面上的特殊图形(如三角形)(称之为斜面)在另一个面上的射影面(称之为射影面)——求出斜面面积S斜与射影面的面积S射——cos<锐二面角>=S射/S斜。
【应用点】
1.⑴在正三棱柱ABC-A1B1C1中,D为AC的中点,AB1⊥BC1,则二面角D-BC1-C的大小为(
)
A.45°
B.60°
C.90°
D.135°
⑵已知平面α与β所成的二面角为80°,P为α、β外一定点,过点P的一条直线与α、β所成的角都是30°,则这样的直线有且仅有(
)
A.1条
B.2条
C.3条
D.4条
⑶二面角为,直线,直线,则直线与所成的角取值范围是(
)
A.
B.
C.
D.
2.如图,在直三棱柱ABC-A1B1C1中,AB=BC,D为BB1的中点。设AA1=AC=AB,求二面角A1-AD-C1的大小。
3.如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点。若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值。
4.四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2。求平面PAD和平面PBE所成二面角(锐角)的大小。
5.如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,∠BCF=∠CEF=90°,AD=,EF=2。当AB的长为何值时,二面角A-EF-C的大小为60°?
6.如图,在几何体P-ABCD中,面ABCD为矩形,PA⊥面ABCD,AB=PA=2,当≤AD≤时,求二面角B-PD-C的取值范围。
【核心点】
1.画图、识图;
2.二面角的求法:几何法、代数法。
11.11
距离
【知识点】
1.⑴点点间距离:
⑵点到直线的距离:
⑶点到平面的距离:
2.⑴两条平行直线间距离:
⑵两条异面直线间的距离:
⑶一条直线与一个平面平行,这条直线与这个平面间的距离:
3.两个平行平面间的距离:
【应用点】
1.⑴某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长棱的棱长是( )
A.
B.
C.
D.3
⑵已知二面角α-l-β为60°,动点P、Q分别在α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为(
)
A.
B.1
C.
D.2
⑶正方体ABCD?A1B1C1D1的棱长为2,点M为CC1的中点,点N为线段DD1上靠近D1的三等分点,平面BMN交AA1于点Q,则线段AQ的长为( )
A.
B.
C.
D.
⑷用六个完全相同的正方形围成的立体图形叫正六面体。已知正六面体ABCD-A1B1C1D1的棱长为4,则平面AB1D1与平面BC1D间的距离为(
)
A.
B.
C.
D.2
⑸在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=1,则点B到平面D1AC的距离等于________.
2.如图,已知四棱锥P?ABCD,底面ABCD为正方形,且PA⊥底面ABCD,过AB的平面ABFE与侧面PCD的交线为EF,且满足S△PEF∶S四边形CDEF=1∶3.
(1)证明:PB∥平面ACE;
(2)当PA=2AD=2时,求点F到平面ACE的距离.
3.如图,多面体ABCD-A1B1C1D1中,AA1、BB1、CC1、DD1均垂直于平面ABCD,AD∥BC,AB=BC=CD=AA1=CC1=2,BB1=1,AD=DD1=4。
⑴求直线AC与平面A1B1C1的距离;
⑵求直线BC1与平面A1B1C1所成角的正切值。
4.正方体ABCD?A1B1C1D1的棱长为2,点E为B1C1的中点.
⑴求证平面BDE与平面A1B1C1D1的交线过C1D1的中点;
⑵求点C1到平面BDE的距离。
【核心点】
1.画图、识图;
2.两个平行平面间的距离,直线与平面间的距离→点到平面的距离;直线与直线的距离、点到直线的距离→点点间的距离。
11.12
体积
【知识点】
柱体体积:
锥体体积:
台体体积:
球体体积:
【应用点】
1.⑴设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D?ABC体积的最大值为( )
A.12 B.18
C.24
D.54
⑵在棱长为1的正方体ABCD?A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F将点B1所在的几何体削去,则剩余几何体的体积为( )
A.
B.
C.
D.
⑶已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________.
⑷已知三棱锥S?ABC的顶点都在球O的球面上,△ABC是边长为3的正三角形,SC为球O的直径,且SC=4,则此三棱锥的体积为________.
⑸如图,圆形纸片的圆心为O,半径为5
cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为________.
2.在四面体P?ABC中,AB=BC=2,∠ABC=120°,PA=PB=PC=4,求四面体P?ABC的体积.
3.在四面体ABCD中,若有5条棱长均为3,只有一条棱长为4,求此四面体的体积.
4.在四面体D?ABC中,三组对棱分别相等,且依次为2,2,2,求此四面体的体积.
5.三棱锥的三条侧棱两两垂直,3个侧面与底面所成的角分别为30°,45°,60°,底面面积为,求三棱锥的体积.
6.如图多面体ABCDEF中,四边形ABCD是边长为2的菱形,∠DAB=60°.EF∥AC,EA=ED=EF=.
(1)求AD与BE所成的角;
(2)若BE=,求三棱锥B?CDF的体积.
【核心点】
1.画图、识图;
2.体积的求法:直接法、分割法、补形法。
11.13
球
【知识点】
1.球的截口是一个圆,该圆半径的平方=球的半径的平方-
的平方
2.球心的确定:
多面体的外接球球心到多面体各顶点距离相等,内切球球心到多面体各面的距离相等。
⑴正方体的外接球、内切球球心均是体对角线的
;长方体的外接球球心是体对角线的
,长方体不一定有内切球;
⑵正棱柱的外接球球心是上下底面中心的连线的
,正棱柱不一定有内切球;
⑶直三棱柱的外接球球心是上下底面的
心的连线的
,但不一定有内切球;
⑷正棱锥的外接球、内切球球心都在该棱锥的
上;
⑸若多面体中有三条共点且两两互相垂直的线段,可借助这三条线段构建长方体确定球心;
⑹通过构建三角形找球心
3.研究透彻六个球:正方体的外接球、棱切球、内切球,正四面体的外接球、棱切球、内切球。
【应用点】
1.⑴已知球O与棱长为4的正四面体的各棱相切,则球O的体积为( )
A.π B.π
C.π
D.π
⑵如图,一个三棱锥的三视图均为直角三角形.若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )
A.4π
B.16π
C.24π
D.25π
⑶把一个皮球放入如图所示的由8根长均为20
cm的铁丝接成的四棱锥形骨架中,使皮球的表面与8根铁丝都有接触点(皮球不变形),则皮球的半径为( )
A.10
cm
B.10
cm
C.10
cm
D.30
cm
⑷三棱锥P?ABC的四个顶点都在体积为的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
A.4
B.6
C.8
D.10
⑸已知圆柱的高为2,底面半径为,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于( )
A.4π
B.π
C.π
D.16π
⑹已知底面半径为1,高为的圆锥的顶点和底面圆周都在球O的球面上,则球O的表面积为( )
A.
B.4π
C.
D.12π
2.⑴已知三棱柱A1B1C1?ABC内接于球O,AB=AC=24,∠BAC=120°,AA1⊥平面ABC,AA1=14,则球O的表面积是________.
⑵在三棱锥V?ABC的四个面中,有两个面都是直角边为1的等腰直角三角形,另两个面都是直角边分别为1和的直角三角形,则该三棱锥的外接球的体积为________.
⑶在正四棱锥P-ABCD中,底面ABCD是边长为4的正方形,E、F分别是AB、CD的中点,cos∠PEF=,若A、B、C、D、P在同一球面上,则此球的体积为
。
⑷三棱台ABC-A1B1C1中,A1A=B1B=C1C=A1B1=2,AB=4,侧面A1B1BA⊥底面ABC,则该三棱台的外接球的表面积是
。
【核心点】
1.画图、识图;
2.解与球相关的组合体问题的策略:
(1)过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题.
(2)利用平面几何知识寻找几何体中元素间的关系,或通过画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
11.14
折叠问题
【应用点】
1.⑴已知矩形ABCD,AB=4,AD=2,E为AB的中点,沿直线DE将△ADE翻折成△PDE,直线PB与平面BCDE所成角最大时PB的长是(
)
A.
B.
C.
D.
⑵已知C为Rt△ABD斜边BD上一点,且△ACD为正三角形,将△ABC沿AC翻折到△AB/C,若在三棱锥B/—ACD中,直线CB/、AB/与平面ACD所成的角分别为α、β,则(
)
A.0<α<β
B.β<α≤2β
C.2β≤α≤3β
D.3β≤α
⑶在矩形ABCD中,AB=2,BC=1,E、N分别为边AB、BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为A1D、A1C的中点,则在△ADE折起的过程中(
)
A.DE可以与A1C垂直
B.不可能同时做到MN∥平面A1BE且BK∥平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.
直线A1E、BK与平面BCDE所成的角能够同时取得最大值
⑷(多选题)如图,在正方形ABCD中,AC为对角线,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H.下列说法错误的是(
)
A.AG⊥△EFH所在平面
B.AH⊥△EFH所在平面
C.HF⊥△AEF所在平面
D.HG⊥△AEF所在平面
⑸如图,在矩形ABCD中,2AB=BC=2,AE=CF=1,将A、C分别沿BE、DF向上翻折至A/、C/,则A/C/取最小值时,二面角A/-EF-C/的余弦值是
。
2.如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
3.如图①,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图②所示的四棱锥D1?ABCE,其中平面D1AE⊥平面ABCE.
(1)设F为CD1的中点,试在AB上找一点M,使得MF∥平面D1AE;
(2)求直线BD1与平面CD1E所成的角的正弦值.
4.已知直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AD=,AB=1,如图①所示,将△ABD沿BD折起到△PBD的位置得三棱锥P?BCD,如图②所示.
(1)求证:BD⊥PC;
(2)当平面PBD⊥平面PBC时,求二面角P?DC?B的大小.
【核心点】
1.画图、识图;
2.注意折叠前后变化的量与不变化的量。
11.15
存在性问题
【应用点】
1.如图,在四棱锥P?ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.
(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M?AC?D的大小为45°?若存在,求BM与平面MAC所成角的正弦值;若不存在,请说明理由.
2.如图,在四棱锥E?ABCD中,底面ABCD为直角梯形,其中CD∥AB,BC⊥AB,侧面ABE⊥平面ABCD,且AB=AE=BE=2BC=2CD=2,动点F在棱AE,且EF=λFA.
(1)试探究λ的值,使CE∥平面BDF,并给予证明;
(2)当λ=1时,求直线CE与平面BDF所成角的正弦值.
3.边长为4的正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点,现将△ABC沿CD翻折成直二面角A-DC-B。
⑴求二面角E-DF-C的余弦值;
⑵在线段BC上是否存在点P,使AP⊥DE?若存在,试指出点P的位置;若不存在,请说明理由。
4.在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,△PAD是边长为2的正三角形,PC=,E为线段AD的中点。
⑴求证:平面PBC⊥平面PBE;
⑵是否存在满足=(>0)的点F,使得VB-PAE=VD-PFB?若存在,则求出的值;若不存在,请说明理由。
5.棱柱ABCD?A1B1C1D1的所有棱长都等于2,平面AA1C1C⊥平面ABCD,∠ABC=∠A1AC=60°。
⑴求二面角D-A1A-C的余弦值;
⑵在直线CC1上是否存在点P,使得BP平面DA1C1?
若存在,求出点P的位置;若不存在,请说明理由。
6.四边形ABCD是圆柱OO1的轴截面,点P是底面圆周上异于A、B的一点,若圆柱的侧面积为2,体积为,点Q是DP上靠近点D的三等分点,是否存在点P,使得直线AQ与平面BDP所成的角正弦值最大?若存在,求出相应的正弦值,并指出点P的位置;若不存在,请说明理由。
7.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,M是线段EF的中点,AB=,AF=t。
⑴若t=1,求二面角A-DF-B的大小;
⑵若线段AC上总存在一点P,使得PF⊥BE,求t的最大值。
【核心点】
1.画图、识图;
2.解决问题的方法:几何法、向量法
11.16
截面、展开
【应用点】
1.已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )
A.
B.
C.
D.
2.侧棱长为2a的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为(
)
A.
2a
B.6a
C.4a
D.12a
3.在棱长均为2的正四面体ABCD中,M为AC的中点,E为AB的中点,P是DM上的动点,Q是平面ECD上的动点,则AP+PQ的最小值是(
)
A.
2
B.
C.+
D.
4.在正方体ABCD?A1B1C1D1中,平面α垂直于对角线AC且截正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则(
)
A.S为定值,l不为定值
B.S不为定值,l为定值
C.S、l均为定值
D.S、l均不为定值
5.(多选题)直三棱柱ABC-A1B1C1的所有棱长都是4,P、Q、R分别是AA1、AB、B1C1上的点,AP=AQ=2,B1R=3,过P、Q、R三点的平面将三棱柱分为两部分,下列说法正确的是(
)
A.截面是五边形
B.截面面积为3
C.截面将三棱柱体积平分
D.截面与底面所成锐二面角的大小为60°
6.过棱长为1的正方体的一条体对角线作截面,则截得正方体的截面面积的最小值是(
)
A.
1
B.
C.
D.
7.某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A.2
B.2
C.3
D.2
8.正四面体ABCD的外接球半径为2,过棱AB作该球的截面,则截面面积的最小值为________.
【核心点】
画图、识图;
11.17
综合问题
【知识点】
1.转化思想:空间问题平面化,几何问题向量化,几何问题代数化(建立空间坐标系)。
2.平行与垂直的证明:由条件想性质,由结论想判定。
3.空间三种角的求法:①几何法:作——证——求。②向量法。
4.距离求法:各种距离转化为两点间距离或点到平面的距离(等体积法)。
【应用点】
1.已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为。
⑴证明BF∥平面ADE;
⑵△ACD为正三角形,判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结
论,并求角的余弦值。
2.如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA、PB、AC的中点,AC=16,PA=PC=10。
⑴设G是OC的中点,证明:FG∥平面BOE;
⑵证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离。
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°.点D,E分别在棱PB,PC上,且DE∥BC.
⑴求证:BC⊥平面PAC;
⑵当D为PB的中点时,求AD与平面PAC所成的角的大小;
⑶是否存在点E使得二面角A-DE-P为直二面角?并说明理由。
4.四棱锥P?ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M?AB?D的余弦值.
5.如图,在四棱锥P?ABCD中,E,F分别是PC,PD的中点,底面ABCD是边长为2的正方形,PA=PD=2,且平面PAD⊥平面ABCD.
(1)求证:平面AEF⊥平面PCD;
(2)求平面AEF与平面ACE所成锐二面角的余弦值.
6.如图,三棱柱ABC?A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
(1)当为何值时,平面CDG⊥平面A1DE?
(2)求平面A1BF与平面A1DE所成的锐二面角的余弦值.
7.如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
(1)求证:AC⊥平面BDEF;
(2)求直线DH与平面BDEF所成角的正弦值;
(3)求二面角H?BD?C的大小.
8.如图,在四棱锥P?ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB.
(1)求证:BE∥平面PAD;
(2)若二面角P?CD?A的正切值为2,求直线PB与平面PCD所成角的正弦值.
9.如图,已知平行四边形ABCD与△EMN所在的平面都与矩形BDEF所在的平面垂直,且∠BAD=60°,AB=MN=2AD=2,EM=EN,F为MN的中点.
(1)求证:MN∥AD;
(2)若直线AE与平面ABCD所成的角为60°,求二面角M?AB?C的余弦值.
10.如图,在三棱锥P?ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M?PA?C为30°,求PC与平面PAM所成角的正弦值.
11.如图,在四棱锥P?ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD,E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P?AC?E的余弦值为,求直线PA与平面EAC所成角的正弦值.
12.如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1。
⑴证明AB=AC
;
⑵设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小。
13.在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2。以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N。
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;
(3)求点N到平面ACM的距离。
14.如图,四棱锥S—ABCD的底面是正方形,SD平面ABCD,SD=2a,AD=a,点E是SD上的点,且DE=a(0<≤2)。
⑴求证:对任意的0<≤2,都有AC⊥BE;
⑵设二面角C—AE—D的大小为,直线BE与平面ABCD所成的角为,若,求的值
。
15.如图,在五面体ABCDEF中,FA
平面ABCD,AD//BC//FE,ABAD,M为EC的中点,AF=AB=BC=FE=AD。
⑴求异面直线BF与DE所成的角的大小;
⑵证明平面AMD平面CDE;
⑶求二面角A-CD-E的余弦值。
【核心点】
识图、画图;
两种方法:几何法、向量法。2021-2022编者-龙诗春215
同课章节目录
