集合与常用逻辑用语 教案 2022届高三数学一轮复习(Word无答案)
文档属性
| 名称 | 集合与常用逻辑用语 教案 2022届高三数学一轮复习(Word无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 20:00:12 | ||
图片预览




文档简介
1.1
集合、集与集的关系
【知识点】
1.集合:一些
的总体,其中的各个
统称为元素.集合中的元素可以是数、点、物品、图形、人、植物、动物等.
⑴元素的特点①确定性,②
,③
.
⑵元素与集合的关系:a是集A的元素a A;a不是集A的元素a A.
集合的表示
⑴字母表示:①A、B、C、…;
②特殊数集:自然数集
、正整数集 、整数集 、有理数集 、实数集 、复数集 .
⑵列举法:把集合的元素
出来,并用“ ”括起来.
⑶描述法:
.
⑷图形表示:
①任何一个集合都可用平面上
的内部表示;
②一些实数构成的集合可以用
表示;
③一些形如(x,y)的元素构成的集合可通过所满足的条件画出具体的曲线或平面区域.
⑸区间表示:{x|a≤x≤b}=
,{x|a<x<b}=
,{x|a<x≤b}=
,{x|a≤x<b}=
,{x|x≤b}=
,{x|a≤x
}=
,{x|x<b}=
,{x|a<x}=
,{x|x<a,或x>b}=
.
3.空集:不含 的集合,记为 .
4.集合间的基本关系
(1)A是B的子集A中的 元素都是B的元素a∈A,a
BA B;
(2)A不是B的子集A中 元素不是B的元素a∈A,a
BA B;
(3)A=BA的元素与B的元素 A B,且B A;
(4)A是B的真子集A中的 元素都是B的元素,且B中 元素不在A中 a∈A,a
B,且 b∈B,b
AA B;
(5)结论:A,
A.
含有n个元素的集合的子集有
个,真子集有
个.
5.全集:含有研究问题中涉及的所有元素的集合;.
【应用点】
1.下列用列举法表示集合{(x,y)|2x+y=6且x-y=3}正确的是( )
A.{x=3,y=0}
B.{0,3}
C.{(0,3)}
D.{(3,0)}
2.若集合中的元素是的三边长,则△一定不是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.集M={x|x=+,kZ},N={x|x=+,kZ},则( )
A.MN
B.M=N
C.NM
D.2022MN
4.集M={x||x|≤1},N={y|y=x2,xM},则( )
A.MN
B.M=N
C.NM
D.MN=
5.集A={xR|x2+x-6=0},B={xR|ax-1=0},BA,则实数a取值的集合是( )
A.{-,} B.{-,} C.{-,0,} D.{-,0,}
6.集A={xR|2≤x≤4},B={xR|2a≤x≤a+3},BA,则实数a取值的集合是( )
A.[1,3]
B.{1}∪(3,+∞)
C.{1}
D.(3,+∞)
7.集A={1,2,3,4,5},B={(x,y)|xA,yA,x-yA},则B的非空真子集的个数是( )
A.6
B.62
C.254
D.1022
8.集A={(x,y)|y≥x,xN+,yN+},B={(x,y)|x+y=8},则A∩B的子集的个数是( )
A.4
B.8
C.16
D.64
9.有限集合P中元素的个数记为card(P).已知card(M)=10,AM,BM,A∩B=,且card(A)=2,card(B)=3.若集X满足XM,且AX,BX,则集X的个数是( )
A.672
B.640
C.384
D.352
10.已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A?B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A?B中元素的个数为( )
A.77
B.49
C.45
D.30
11.集A={(x,y)|x2+y2≤3,xZ,yZ},B={(x,y)|y2=x},C=A∩B,从集A中任取一个元素,则所取元素是C的元素的概率是 .
【核心点】
1.构成集合的是元素;
2.判断两个集合之间的关系,关键是弄清楚集合中的元素.
1.2
集合的运算
【知识点】
1.交集:A∩B=A与B的
元素构成的集合
={x|x A, x B}=如图阴影部分 .
2.并集:A∪B=A的元素与B的元素
构成的集合
={x|x A, x B}=如图阴影部分 .
3.补集:AU,则CUA=U中
A的元素 的元素构成的集合
={x|x U, x A}=如图阴影部分 .
【应用点】
1.集A={1,2,3,4},B={y|y=3x-2,xA},则集合A∩B=( )
A.{1}
B.{4}
C.{1,3}
D.{1,4}
2.集A={x|x2-3x-4<0},B={1,5,3,-4},则集合A∩B=( )
A.{-4,1}
B.{1,5}
C.{5,3}
D.{1,3}
3.集U={-2,-1,0,1,2,3},A={-1,0,1},B={2,1},则集合CU(A∪B)=( )
A.{-2,3}
B.{-2,3,2}
C.{-2,-1,0,3}
D.{-2,-1,0,2,3}
4.集A={xR|-1<x<1},B={xR|0<x<2},则集合A∪B=( )
A.(-1,2)
B.(0,1)
C.(-1,0)
D.(1,2)
5.集A={xR|x2-4≤0},B={xR|2x+a≤0},且A∩B={xR|-2≤x≤1},则a=( )
A.-4
B.-2
C.2
D.4
6.集A={1,2,4},B={xR|x2-4x+m=0},若A∩B={1},则集合B=( )
A.{-3,1}
B.{1,0}
C.{1,3}
D.{1,5}
7.集A={1,3,},B={1,},A∪B=A,则=( )
A.0,或3
B.1,或3
C.0,或
D.1,或
8.常数aR,集A={xR|(x-1)(x-a)≥0},B={xR|x≥a-1},且A∪B=R,则实数a取值范
围是( )
A.(-∞,2)
B.(-∞,2]
C.(2,+∞)
D.[2,+∞)
9.全集为R,集A={xR|->0},B={xR|<-1},则下列关系中正确的是( )
A.A∪B=R
B.A∩B=A
C.(CRA)∪B=R
D.CRACRB
10.集A={a-1,a+1},B={1,2},C={2,3},若A∩B=,且A∩C≠,则a=( )
A.2,或4
B.1,或3
C.0
D.4
11.集M={(x,y)|y=x+b},N={(x,y)|y=3-},M∩N≠,则实数b取值范围是
.
【核心点】
1.进行集合运算首先必须弄清集合的元素;
2.集合的并、交、补对应的逻辑联结词分别是“或,且,非”;
3.树立集合观,将要研究的对象置于一个系统内即集合内,然后在这个集合内进行研究.
1.3
命题及其关系、简单的逻辑联结词
【知识点】
1.命题:可以判断
的
句;判断为
的命题称为真命题,判断为
的命题称为假命题;命题的构成形式: ,即“条件+结论”.
2.对于两个命题
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互逆命题,一个命题叫
,另一个命题称为
.
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互否命题,一个命题叫
,另一个命题称为
.
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互为逆否命题,一个命题叫
,另一个命题称为
.
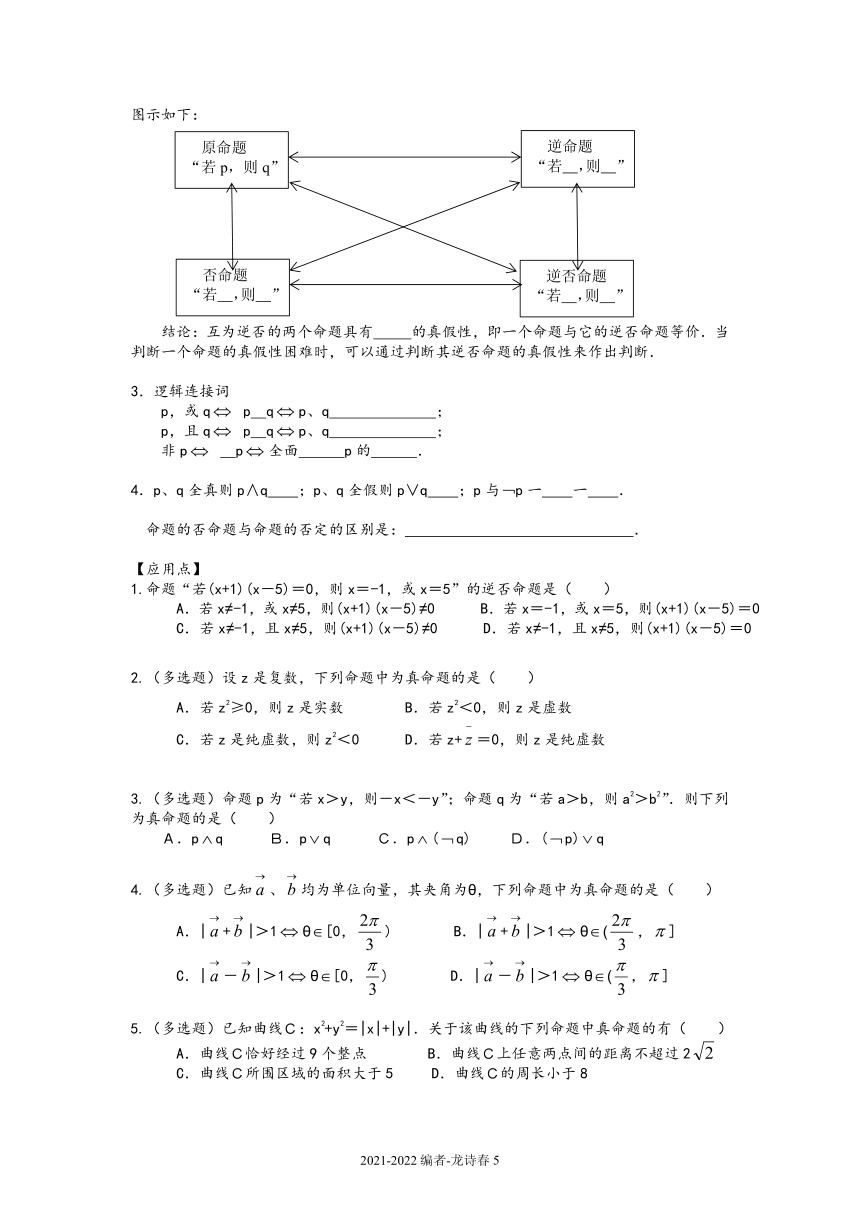
图示如下:
结论:互为逆否的两个命题具有
的真假性,即一个命题与它的逆否命题等价.当判断一个命题的真假性困难时,可以通过判断其逆否命题的真假性来作出判断.
3.逻辑连接词
p,或q
p
qp、q ;
p,且q
p
qp、q ;
非p
p全面 p的 .
4.p、q全真则p∧q
;p、q全假则p∨q
;p与﹁p一
一
.
命题的否命题与命题的否定的区别是:
.
【应用点】
1.命题“若(x+1)(x-5)=0,则x=-1,或x=5”的逆否命题是( )
A.若x≠-1,或x≠5,则(x+1)(x-5)≠0
B.若x=-1,或x=5,则(x+1)(x-5)=0
C.若x≠-1,且x≠5,则(x+1)(x-5)≠0
D.若x≠-1,且x≠5,则(x+1)(x-5)=0
2.(多选题)设z是复数,下列命题中为真命题的是( )
A.若z2≥0,则z是实数
B.若z2<0,则z是虚数
C.若z是纯虚数,则z2<0
D.若z+=0,则z是纯虚数
3.(多选题)命题p为“若x>y,则-x<-y”;命题q为“若a>b,则a2>b2”.则下列为真命题的是( )
A.pq
B.pq
C.p(q)
D.(p)q
4.(多选题)已知、均为单位向量,其夹角为θ,下列命题中为真命题的是( )
A.|+|>1θ[0,)
B.|+|>1θ(,]
C.|-|>1θ[0,)
D.|-|>1θ(,]
5.(多选题)已知曲线C:x2+y2=|x|+|y|.关于该曲线的下列命题中真命题的有( )
A.曲线C恰好经过9个整点
B.曲线C上任意两点间的距离不超过2
C.曲线C所围区域的面积大于5
D.曲线C的周长小于8
6.命题“若z1、z2是共轭复数,则|z1|=|z2|”的逆命题、否命题、逆否命题的真假性的判断依次如下,正确的是( )
A.真、假、真
B.假、假、真
C.真、真、假
D.假、假、假
7.设集合S、T,SN
,TN
,S、T中至少有2个元素,且S、T满足:①对于任意x、yS,若x≠y,则xyT;②对于任意x、yT,若x<y,则S;
下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
8.命题p:函数f(x)=的定义域为R;命题q:xR满足ax≤lnx;若pq为真,则实数a取值范围是( )
A.[-2,]
B.[,2]
C.(-∞,-2]
D.[2,+∞)
【核心点】
1.
对于带“或”、“且”命题的否定,“不或即且,不且即或”.
2.一个命题的真假难作判断,可转化为对它的逆否命题的判断.
3.一个命题的真假难作判断,可转化为对它的否定的判断.
1.4充分条件、必要条件
【知识点】
1.p是q的充分不必要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的必要不充分条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的充要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的不充分不必要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”.
等价语言:p是q的充分不必要条件q的充分不必要条件是p
p是q的必要不充分条件q的必要不充分条件是p
p是q的充要条件q的充要条件是p
p是q的不充分不必要条件q的不充分不必要条件是p
2.若满足条件p的元素构成的集合是A,满足条件q的元素构成的集合是B,则
p是q的充分非必要条件A
B;
p是q的必要非充分条件A
B;
p是q的充分必要条件A
B;
p是q的非充分非必要条件A
B且A
B.
【应用点】
1.下列表格中的前提条件下p是q的什么条件,请选“充分不必要条件、必要不充分条件、充要条件、不充分不必要条件”其中之一填写:
前提条件
p
q
p是q的什么条件
xR
|x+1|≤2
5x-6≤x2
a≠1,或b≠2
a+b≠3
ABC是斜三角形
A>B
|tanA|>|tanB|
≠,≠
<0
<0,使得=
i是虚数单位,a、bR
a=b=1
(a+bi)2=2i
直线a、b分别在两个不
同的平面、内
a和b相交
和相交
{an}是首项为正数、公比
为q的等比数列
q<0
nN+,a2n-1+a2n<0
2.函数f(x)=|x-a|在区间[5,+∞)上为增函数的
⑴一个充要条件是实数a取值范围为 ;
⑵一个必要非充分条件是实数a取值范围为 ;
⑶一个充分非必要条件是实数a取值范围为 .
3.⑴x>1是2x>a-x的充要条件,则a的值为
;
⑵x>1是2x>a-x的充分不必要条件,则a的最大整数值为
;
⑶x>1是2x>a-x的必要不充分条件,则a的最小整数值为
;
4.A(x1,y1)、B(c,)、C(x2,y2)是右焦点为F(c,0)的椭圆+=1上三个不同的点,求|AF|、|BF|、|CF|成等差数列的充要条件.
5.数列{an}的前n项和为Sn,求证:数列{an}为等差数列的充要条件是Sn=.
【核心点】
1.怎样判断两个条件间的关系?
2.等价关系(等价转化思想)即为充要条件关系.
1.5
全称量词与存在量词
【知识点】
1.一些常见对应词
肯定词
是(一定是)
都是(全是)
>(<)
至少有一个
至多有一个
=
存在
否定词
2.全称量词:“所有的”“任意一个”“一切”“每一个”“任给”等,常用“”表示.含有全称量词的命题叫全称命题(或全称量词命题).
存在量词:“存在一个”“至少有一个”“有些”“有一个”“有的”
“对某个”等,常用“”表示.含有存在量词的命题叫特称命题(或存在量词命题).
3.含有量词、逻辑联结词的命题的否定
全称命题p:x∈M,p(x),则﹁p:
;
特称命题p:x0∈M,p(x0),则﹁p:
;
“p或q”的否定:
; “p且q”的否定:
.
4.常用结论
xD,f(x)≥aa≤ ; xD,f(x)≥aa≤ ;
xD,f(x)≤aa≥ ; xD,f(x)≤aa≥ .
【应用点】
在下列表格中写出命题p的否定
p
p
nN,n2>2n
xR,x2≠x
n0N+,使f(n0)N+且f(n0)≤n0
对于集A、B,xA∪B,xA或xB
xR,n0N+,使n>x2
2.若命题“x0R,x02+(a-1)x0+1<0”的否定是假命题,则实数a取值范围为 .
3.已知x2+4x+2≤2kex(x+1)对x[-2,+∞)都成立,求k的取值范围.
4.已知函数f(x)=(x+1)2-ln(x+1)2,g(x)=x2+x+a.若存在x[0,2]使得f(x)≥g(x)成立,求a的取值范围.
5.已知函数
⑴当≤时,讨论的单调性;
⑵设当时,若对任意,存在,使f(x1)≥g(x2),求实数取值范围.
【核心点】
1.对于带量词的命题的否定,“全称量词与存在量词要互换”.
2.带量词的含参命题可相互转化
aU,“‘xD,f(x)≥a成立’aA”“‘xD,f(x)”,这里用的是集合的
思想.
3.x1A,x2B,使f(x1)≥g(x2)f(x)min≥g(x)min;x1A,x2B,使f(x1)≥g(x2)成立f(x)min≥g(x)max。2021-2022编者-龙诗春1
集合、集与集的关系
【知识点】
1.集合:一些
的总体,其中的各个
统称为元素.集合中的元素可以是数、点、物品、图形、人、植物、动物等.
⑴元素的特点①确定性,②
,③
.
⑵元素与集合的关系:a是集A的元素a A;a不是集A的元素a A.
集合的表示
⑴字母表示:①A、B、C、…;
②特殊数集:自然数集
、正整数集 、整数集 、有理数集 、实数集 、复数集 .
⑵列举法:把集合的元素
出来,并用“ ”括起来.
⑶描述法:
.
⑷图形表示:
①任何一个集合都可用平面上
的内部表示;
②一些实数构成的集合可以用
表示;
③一些形如(x,y)的元素构成的集合可通过所满足的条件画出具体的曲线或平面区域.
⑸区间表示:{x|a≤x≤b}=
,{x|a<x<b}=
,{x|a<x≤b}=
,{x|a≤x<b}=
,{x|x≤b}=
,{x|a≤x
}=
,{x|x<b}=
,{x|a<x}=
,{x|x<a,或x>b}=
.
3.空集:不含 的集合,记为 .
4.集合间的基本关系
(1)A是B的子集A中的 元素都是B的元素a∈A,a
BA B;
(2)A不是B的子集A中 元素不是B的元素a∈A,a
BA B;
(3)A=BA的元素与B的元素 A B,且B A;
(4)A是B的真子集A中的 元素都是B的元素,且B中 元素不在A中 a∈A,a
B,且 b∈B,b
AA B;
(5)结论:A,
A.
含有n个元素的集合的子集有
个,真子集有
个.
5.全集:含有研究问题中涉及的所有元素的集合;.
【应用点】
1.下列用列举法表示集合{(x,y)|2x+y=6且x-y=3}正确的是( )
A.{x=3,y=0}
B.{0,3}
C.{(0,3)}
D.{(3,0)}
2.若集合中的元素是的三边长,则△一定不是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.集M={x|x=+,kZ},N={x|x=+,kZ},则( )
A.MN
B.M=N
C.NM
D.2022MN
4.集M={x||x|≤1},N={y|y=x2,xM},则( )
A.MN
B.M=N
C.NM
D.MN=
5.集A={xR|x2+x-6=0},B={xR|ax-1=0},BA,则实数a取值的集合是( )
A.{-,} B.{-,} C.{-,0,} D.{-,0,}
6.集A={xR|2≤x≤4},B={xR|2a≤x≤a+3},BA,则实数a取值的集合是( )
A.[1,3]
B.{1}∪(3,+∞)
C.{1}
D.(3,+∞)
7.集A={1,2,3,4,5},B={(x,y)|xA,yA,x-yA},则B的非空真子集的个数是( )
A.6
B.62
C.254
D.1022
8.集A={(x,y)|y≥x,xN+,yN+},B={(x,y)|x+y=8},则A∩B的子集的个数是( )
A.4
B.8
C.16
D.64
9.有限集合P中元素的个数记为card(P).已知card(M)=10,AM,BM,A∩B=,且card(A)=2,card(B)=3.若集X满足XM,且AX,BX,则集X的个数是( )
A.672
B.640
C.384
D.352
10.已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A?B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A?B中元素的个数为( )
A.77
B.49
C.45
D.30
11.集A={(x,y)|x2+y2≤3,xZ,yZ},B={(x,y)|y2=x},C=A∩B,从集A中任取一个元素,则所取元素是C的元素的概率是 .
【核心点】
1.构成集合的是元素;
2.判断两个集合之间的关系,关键是弄清楚集合中的元素.
1.2
集合的运算
【知识点】
1.交集:A∩B=A与B的
元素构成的集合
={x|x A, x B}=如图阴影部分 .
2.并集:A∪B=A的元素与B的元素
构成的集合
={x|x A, x B}=如图阴影部分 .
3.补集:AU,则CUA=U中
A的元素 的元素构成的集合
={x|x U, x A}=如图阴影部分 .
【应用点】
1.集A={1,2,3,4},B={y|y=3x-2,xA},则集合A∩B=( )
A.{1}
B.{4}
C.{1,3}
D.{1,4}
2.集A={x|x2-3x-4<0},B={1,5,3,-4},则集合A∩B=( )
A.{-4,1}
B.{1,5}
C.{5,3}
D.{1,3}
3.集U={-2,-1,0,1,2,3},A={-1,0,1},B={2,1},则集合CU(A∪B)=( )
A.{-2,3}
B.{-2,3,2}
C.{-2,-1,0,3}
D.{-2,-1,0,2,3}
4.集A={xR|-1<x<1},B={xR|0<x<2},则集合A∪B=( )
A.(-1,2)
B.(0,1)
C.(-1,0)
D.(1,2)
5.集A={xR|x2-4≤0},B={xR|2x+a≤0},且A∩B={xR|-2≤x≤1},则a=( )
A.-4
B.-2
C.2
D.4
6.集A={1,2,4},B={xR|x2-4x+m=0},若A∩B={1},则集合B=( )
A.{-3,1}
B.{1,0}
C.{1,3}
D.{1,5}
7.集A={1,3,},B={1,},A∪B=A,则=( )
A.0,或3
B.1,或3
C.0,或
D.1,或
8.常数aR,集A={xR|(x-1)(x-a)≥0},B={xR|x≥a-1},且A∪B=R,则实数a取值范
围是( )
A.(-∞,2)
B.(-∞,2]
C.(2,+∞)
D.[2,+∞)
9.全集为R,集A={xR|->0},B={xR|<-1},则下列关系中正确的是( )
A.A∪B=R
B.A∩B=A
C.(CRA)∪B=R
D.CRACRB
10.集A={a-1,a+1},B={1,2},C={2,3},若A∩B=,且A∩C≠,则a=( )
A.2,或4
B.1,或3
C.0
D.4
11.集M={(x,y)|y=x+b},N={(x,y)|y=3-},M∩N≠,则实数b取值范围是
.
【核心点】
1.进行集合运算首先必须弄清集合的元素;
2.集合的并、交、补对应的逻辑联结词分别是“或,且,非”;
3.树立集合观,将要研究的对象置于一个系统内即集合内,然后在这个集合内进行研究.
1.3
命题及其关系、简单的逻辑联结词
【知识点】
1.命题:可以判断
的
句;判断为
的命题称为真命题,判断为
的命题称为假命题;命题的构成形式: ,即“条件+结论”.
2.对于两个命题
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互逆命题,一个命题叫
,另一个命题称为
.
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互否命题,一个命题叫
,另一个命题称为
.
一个命题的
和
分别是另一个命题的
和
,这两个命题称为互为逆否命题,一个命题叫
,另一个命题称为
.
图示如下:
结论:互为逆否的两个命题具有
的真假性,即一个命题与它的逆否命题等价.当判断一个命题的真假性困难时,可以通过判断其逆否命题的真假性来作出判断.
3.逻辑连接词
p,或q
p
qp、q ;
p,且q
p
qp、q ;
非p
p全面 p的 .
4.p、q全真则p∧q
;p、q全假则p∨q
;p与﹁p一
一
.
命题的否命题与命题的否定的区别是:
.
【应用点】
1.命题“若(x+1)(x-5)=0,则x=-1,或x=5”的逆否命题是( )
A.若x≠-1,或x≠5,则(x+1)(x-5)≠0
B.若x=-1,或x=5,则(x+1)(x-5)=0
C.若x≠-1,且x≠5,则(x+1)(x-5)≠0
D.若x≠-1,且x≠5,则(x+1)(x-5)=0
2.(多选题)设z是复数,下列命题中为真命题的是( )
A.若z2≥0,则z是实数
B.若z2<0,则z是虚数
C.若z是纯虚数,则z2<0
D.若z+=0,则z是纯虚数
3.(多选题)命题p为“若x>y,则-x<-y”;命题q为“若a>b,则a2>b2”.则下列为真命题的是( )
A.pq
B.pq
C.p(q)
D.(p)q
4.(多选题)已知、均为单位向量,其夹角为θ,下列命题中为真命题的是( )
A.|+|>1θ[0,)
B.|+|>1θ(,]
C.|-|>1θ[0,)
D.|-|>1θ(,]
5.(多选题)已知曲线C:x2+y2=|x|+|y|.关于该曲线的下列命题中真命题的有( )
A.曲线C恰好经过9个整点
B.曲线C上任意两点间的距离不超过2
C.曲线C所围区域的面积大于5
D.曲线C的周长小于8
6.命题“若z1、z2是共轭复数,则|z1|=|z2|”的逆命题、否命题、逆否命题的真假性的判断依次如下,正确的是( )
A.真、假、真
B.假、假、真
C.真、真、假
D.假、假、假
7.设集合S、T,SN
,TN
,S、T中至少有2个元素,且S、T满足:①对于任意x、yS,若x≠y,则xyT;②对于任意x、yT,若x<y,则S;
下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
8.命题p:函数f(x)=的定义域为R;命题q:xR满足ax≤lnx;若pq为真,则实数a取值范围是( )
A.[-2,]
B.[,2]
C.(-∞,-2]
D.[2,+∞)
【核心点】
1.
对于带“或”、“且”命题的否定,“不或即且,不且即或”.
2.一个命题的真假难作判断,可转化为对它的逆否命题的判断.
3.一个命题的真假难作判断,可转化为对它的否定的判断.
1.4充分条件、必要条件
【知识点】
1.p是q的充分不必要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的必要不充分条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的充要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”;
p是q的不充分不必要条件命题“若p,则q是 ,且若q,则p是 ,”“p
q且q p”.
等价语言:p是q的充分不必要条件q的充分不必要条件是p
p是q的必要不充分条件q的必要不充分条件是p
p是q的充要条件q的充要条件是p
p是q的不充分不必要条件q的不充分不必要条件是p
2.若满足条件p的元素构成的集合是A,满足条件q的元素构成的集合是B,则
p是q的充分非必要条件A
B;
p是q的必要非充分条件A
B;
p是q的充分必要条件A
B;
p是q的非充分非必要条件A
B且A
B.
【应用点】
1.下列表格中的前提条件下p是q的什么条件,请选“充分不必要条件、必要不充分条件、充要条件、不充分不必要条件”其中之一填写:
前提条件
p
q
p是q的什么条件
xR
|x+1|≤2
5x-6≤x2
a≠1,或b≠2
a+b≠3
ABC是斜三角形
A>B
|tanA|>|tanB|
≠,≠
<0
<0,使得=
i是虚数单位,a、bR
a=b=1
(a+bi)2=2i
直线a、b分别在两个不
同的平面、内
a和b相交
和相交
{an}是首项为正数、公比
为q的等比数列
q<0
nN+,a2n-1+a2n<0
2.函数f(x)=|x-a|在区间[5,+∞)上为增函数的
⑴一个充要条件是实数a取值范围为 ;
⑵一个必要非充分条件是实数a取值范围为 ;
⑶一个充分非必要条件是实数a取值范围为 .
3.⑴x>1是2x>a-x的充要条件,则a的值为
;
⑵x>1是2x>a-x的充分不必要条件,则a的最大整数值为
;
⑶x>1是2x>a-x的必要不充分条件,则a的最小整数值为
;
4.A(x1,y1)、B(c,)、C(x2,y2)是右焦点为F(c,0)的椭圆+=1上三个不同的点,求|AF|、|BF|、|CF|成等差数列的充要条件.
5.数列{an}的前n项和为Sn,求证:数列{an}为等差数列的充要条件是Sn=.
【核心点】
1.怎样判断两个条件间的关系?
2.等价关系(等价转化思想)即为充要条件关系.
1.5
全称量词与存在量词
【知识点】
1.一些常见对应词
肯定词
是(一定是)
都是(全是)
>(<)
至少有一个
至多有一个
=
存在
否定词
2.全称量词:“所有的”“任意一个”“一切”“每一个”“任给”等,常用“”表示.含有全称量词的命题叫全称命题(或全称量词命题).
存在量词:“存在一个”“至少有一个”“有些”“有一个”“有的”
“对某个”等,常用“”表示.含有存在量词的命题叫特称命题(或存在量词命题).
3.含有量词、逻辑联结词的命题的否定
全称命题p:x∈M,p(x),则﹁p:
;
特称命题p:x0∈M,p(x0),则﹁p:
;
“p或q”的否定:
; “p且q”的否定:
.
4.常用结论
xD,f(x)≥aa≤ ; xD,f(x)≥aa≤ ;
xD,f(x)≤aa≥ ; xD,f(x)≤aa≥ .
【应用点】
在下列表格中写出命题p的否定
p
p
nN,n2>2n
xR,x2≠x
n0N+,使f(n0)N+且f(n0)≤n0
对于集A、B,xA∪B,xA或xB
xR,n0N+,使n>x2
2.若命题“x0R,x02+(a-1)x0+1<0”的否定是假命题,则实数a取值范围为 .
3.已知x2+4x+2≤2kex(x+1)对x[-2,+∞)都成立,求k的取值范围.
4.已知函数f(x)=(x+1)2-ln(x+1)2,g(x)=x2+x+a.若存在x[0,2]使得f(x)≥g(x)成立,求a的取值范围.
5.已知函数
⑴当≤时,讨论的单调性;
⑵设当时,若对任意,存在,使f(x1)≥g(x2),求实数取值范围.
【核心点】
1.对于带量词的命题的否定,“全称量词与存在量词要互换”.
2.带量词的含参命题可相互转化
aU,“‘xD,f(x)≥a成立’aA”“‘xD,f(x)
思想.
3.x1A,x2B,使f(x1)≥g(x2)f(x)min≥g(x)min;x1A,x2B,使f(x1)≥g(x2)成立f(x)min≥g(x)max。2021-2022编者-龙诗春1
同课章节目录
