小学数学北师大版五年级上数学好玩 3课时 课件(共36张PPT)
文档属性
| 名称 | 小学数学北师大版五年级上数学好玩 3课时 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-25 14:46:01 | ||
图片预览






文档简介
(共36张PPT)
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
学习新知
第1课时
设计秋游方案
学
习
新
知
学校要组织61名学生到故宫和北海公园参观。
活动任务
请帮助他们设计一个合理的秋游方案。
我们这些人需
要多少门票钱?
游玩时间
怎么安排?
1.想一想,设计方案前,先要做哪些方面的准备?
设计方案
2.你想采取怎样的方式设计活动方案?如果是小
组合作,你想怎样进行分工?
3.根据前面的讨论,把要做的准备工作、分工与
要求写下来。
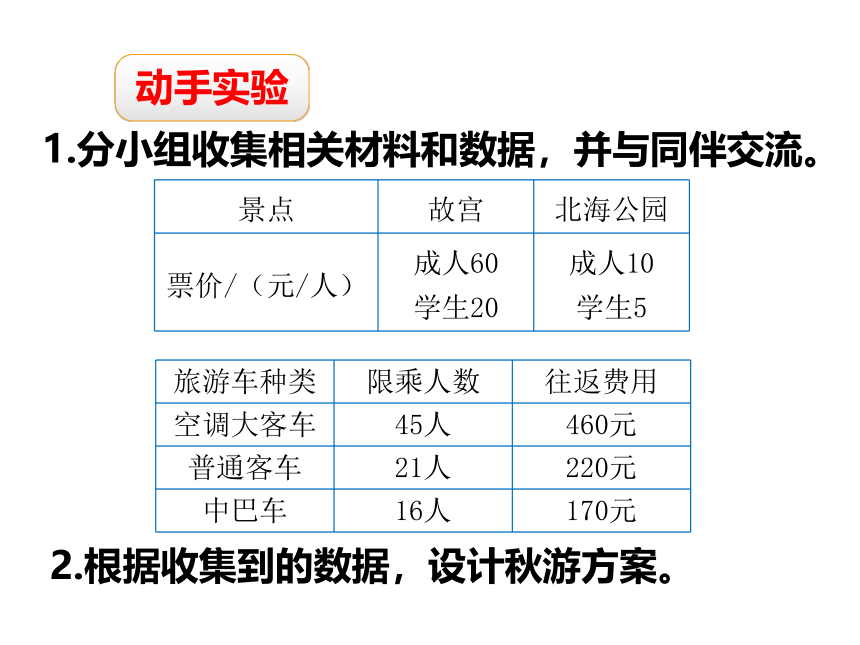
动手实验
景点
故宫
北海公园
票价/(元/人)
成人60
学生20
成人10
学生5
旅游车种类
限乘人数
往返费用
空调大客车
45人
460元
普通客车
21人
220元
中巴车
16人
170元
1.分小组收集相关材料和数据,并与同伴交流。
2.根据收集到的数据,设计秋游方案。
1.全班交流设计的秋游方案,选出合理方案。
交流反思
2.在设计秋游方案的过程中,你用到了哪些数
学知识和方法?
3.下面是某个小组设计的秋游方案,你有什么建议?
返回目录
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
第2课时
图形中的规律
学习新知
随堂练习
复习准备
复
习
准
备
返回目录
摆一个独立的三角形需要几根小棒?两个呢?三个呢?
三根小棒
六根小棒
九根小棒
学
习
新
知
我们来用小棒
摆三角形吧……
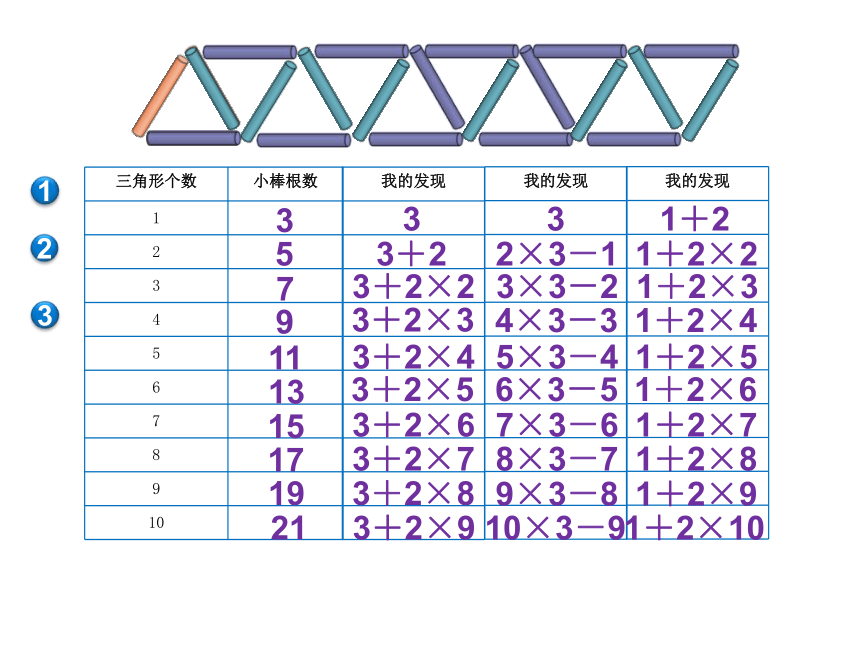
三角形个数和小棒根数
之间总是存在着3倍的
关系。
这是我摆的!
三角形个数
小棒根数
1
2
3
4
5
6
7
8
9
10
3
5
7
9
我的发现
1
2
3
11
13
15
17
19
21
3
3+2
3+2×2
3+2×3
3+2×4
3+2×5
3+2×6
3+2×7
3+2×8
3+2×9
我的发现
3
2×3-1
3×3-2
4×3-3
5×3-4
6×3-5
7×3-6
8×3-7
9×3-8
10×3-9
我的发现
1+2
1+2×2
1+2×3
1+2×4
1+2×5
1+2×6
1+2×7
1+2×8
1+2×9
1+2×10
笑笑接着摆下去,一共用了37根小棒,你知道她摆了多少个三角形吗?
37-3=34
34÷2=17
17+1=18
37-1=36
36÷2=18
观察每个点阵中点的个数,你发现了什么?
1×1
1
2
3
2×2
3×3
4×4
5×5
1+3
1+3+5
1+3+5+7
1
1+2+1
1+2+3+2+1
1+2+3+4+3+2+1
1
返回目录
随堂练习
1.摆图形。小明用小正方形摆“十”
一个
两个
三个
……
摆一个“十”字形需要 个小正方形,摆两个“十”字形需要 个小正方形,摆x个“十”字形需要 个小正方形。
5
10
5x
2.按下图方式摆正方形。
……
摆20个正方形需要多少根小棒?
3×20+1=61(根)
答:摆20个正方形需要61根小棒。
返回目录
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
第3课时
尝试与猜测
学习新知
随堂练习
作业设计
学
习
新
知
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
——我国古代数学名著
《孙子算经》
鸡兔同笼,有9个头,26条腿。鸡、兔各有几只?
列表法
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
…
…
…
画图法
假如9只全是鸡:
一共有2×9=18条腿
还剩26-18=8条腿
4只兔子
5只鸡
砍腿法
如果每只鸡和兔子都先砍去1条腿,那么一共砍去9条腿。再各砍去1条腿,这时鸡就没有腿了,两轮共砍去18条腿,剩下的腿的数量是兔子的,每只兔子剩2条腿,用8条腿除以2条腿就等于兔子只数。
假设法
(1)假设笼子中全是鸡。
腿共有:2×9=18(条)
比实际少了:26-18=8(条)
1只鸡比1只兔子少了:4-2=2(条)
兔子的只数:8÷2=4(只)
鸡的只数:9-4=5(只)
(2)假设笼子中全是兔子。
腿共有:4×9=36(条)
比实际多了:36-26=10(条)
1只兔子比1只鸡多了:4-2=2(条)
鸡的只数:10÷2=5(只)
兔子的只数:9-5=4(只)
跳跃列表法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只
兔有几只
腿有多少条
判断
1
34
2+34×4=138
×
10
25
20+25×4=120
×
20
15
40+15×4=100
×
23
12
46+12×4=94
√
取中列表法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只
兔有几只
腿有多少条
判断
17
18
34+18×4=106
×
20
15
40+15×4=100
×
23
12
46+12×4=94
√
乐乐的储蓄罐里有1角和5角的硬币共27枚,总共是5.1元,1角和5角的硬币各有多少枚?
1角/枚
5角/枚
总值/元
判断
13
14
1.3+14×0.5=8.3
17
10
1.7+10×0.5=6.7
21
6
2.1+6×0.5=5.1
×
×
√
答:1角的硬币有21枚,5角的硬币有6枚。
返回目录
随堂练习
1.停车场里有三轮车和自行车共22辆,
有59个轮子,自行车、三轮车各几辆?
假设停车场里全是自行车。
三轮车:(59-22×2)÷(3-2)
=(59-44)÷1
=15÷1
=15(辆)
自行车:22-15=7(辆)
答:自行车7辆,三轮车15辆。
2.小明的储蓄罐里有1角和5角的硬币共13枚,
总共是2.1元,1角和5角的硬币各有多少枚?
返回目录
假设储蓄罐里全是1角硬币。
5角硬币:(2.1-13×0.1)÷(0.5-0.1)
=(2.1-1.3)÷0.4
=0.8÷0.4
=2(枚)
1角硬币:13-2=11(枚)
答:1角硬币有11枚,5角硬币有2枚。
作业设计
作业1
作业2
要努力哟!
返回目录
作业1
鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只。
假设笼子里全是鸡。
兔:(88-30×2)÷(4-2)
=(88-60)÷2
=28÷2
=14(只)
鸡:30-14=16(只)
答:鸡有16只,兔有14只。
2.鸡兔同笼,共有头48个,脚132只,求鸡和兔各有
多少只。
假设笼子里全是鸡。
兔:(132-48×2)÷(4-2)
=(132-96)÷2
=36÷2
=18(只)
鸡:48-18=30(只)
答:鸡有30只,兔有18只。
3.
一个饲养组一共养鸡、兔78只,共有200只脚,
求饲养组养鸡和兔各多少只。
返回作业设计
假设笼子里全是鸡。
兔:(200-78×2)÷(4-2)
=(200-156)÷2
=44÷2
=22(只)
鸡:78-22=56(只)
答:鸡有56只,兔有22只。
鸡兔同笼不知数,三十六头笼中露。数清脚共五十双,各有多少鸡和兔?
作业2
假设笼子里全是鸡。
兔:(50×2-36×2)÷(4-2)
=(100-72)÷2
=28÷2
=14(只)
鸡:36-14=22(只)
答:鸡有22只,兔有14只。
2.小明用10元钱正好买了20分和50分的邮票共35张,求这两种邮票各买了多少张。
假设小明买的全是20分的邮票。
50分的邮票:(10-35×0.2)÷(0.5-0.2)
=(10-7)÷0.3
=3÷0.3
=10(张)
20分的邮票:35-10=25(张)
答:20分的邮票买了25张,50分的邮票买了10张。
3.小红用13元6角正好买了50分和80分的邮票共20张,求两种邮票各买了多少张。
假设小红买的全是50分的邮票。
80分的邮票:(13.6-20×0.5)÷(0.8-0.5)
=(13.6-10)÷0.3
=3.6÷0.3
=12(张)
50分的邮票:20-12=8(张)
答:50分的邮票买了8张,80分的邮票买了12张。
返回作业设计
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
学习新知
第1课时
设计秋游方案
学
习
新
知
学校要组织61名学生到故宫和北海公园参观。
活动任务
请帮助他们设计一个合理的秋游方案。
我们这些人需
要多少门票钱?
游玩时间
怎么安排?
1.想一想,设计方案前,先要做哪些方面的准备?
设计方案
2.你想采取怎样的方式设计活动方案?如果是小
组合作,你想怎样进行分工?
3.根据前面的讨论,把要做的准备工作、分工与
要求写下来。
动手实验
景点
故宫
北海公园
票价/(元/人)
成人60
学生20
成人10
学生5
旅游车种类
限乘人数
往返费用
空调大客车
45人
460元
普通客车
21人
220元
中巴车
16人
170元
1.分小组收集相关材料和数据,并与同伴交流。
2.根据收集到的数据,设计秋游方案。
1.全班交流设计的秋游方案,选出合理方案。
交流反思
2.在设计秋游方案的过程中,你用到了哪些数
学知识和方法?
3.下面是某个小组设计的秋游方案,你有什么建议?
返回目录
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
第2课时
图形中的规律
学习新知
随堂练习
复习准备
复
习
准
备
返回目录
摆一个独立的三角形需要几根小棒?两个呢?三个呢?
三根小棒
六根小棒
九根小棒
学
习
新
知
我们来用小棒
摆三角形吧……
三角形个数和小棒根数
之间总是存在着3倍的
关系。
这是我摆的!
三角形个数
小棒根数
1
2
3
4
5
6
7
8
9
10
3
5
7
9
我的发现
1
2
3
11
13
15
17
19
21
3
3+2
3+2×2
3+2×3
3+2×4
3+2×5
3+2×6
3+2×7
3+2×8
3+2×9
我的发现
3
2×3-1
3×3-2
4×3-3
5×3-4
6×3-5
7×3-6
8×3-7
9×3-8
10×3-9
我的发现
1+2
1+2×2
1+2×3
1+2×4
1+2×5
1+2×6
1+2×7
1+2×8
1+2×9
1+2×10
笑笑接着摆下去,一共用了37根小棒,你知道她摆了多少个三角形吗?
37-3=34
34÷2=17
17+1=18
37-1=36
36÷2=18
观察每个点阵中点的个数,你发现了什么?
1×1
1
2
3
2×2
3×3
4×4
5×5
1+3
1+3+5
1+3+5+7
1
1+2+1
1+2+3+2+1
1+2+3+4+3+2+1
1
返回目录
随堂练习
1.摆图形。小明用小正方形摆“十”
一个
两个
三个
……
摆一个“十”字形需要 个小正方形,摆两个“十”字形需要 个小正方形,摆x个“十”字形需要 个小正方形。
5
10
5x
2.按下图方式摆正方形。
……
摆20个正方形需要多少根小棒?
3×20+1=61(根)
答:摆20个正方形需要61根小棒。
返回目录
五年级数学·上
新课标[北师]
第6单元
组合图形的面积
数学好玩
第3课时
尝试与猜测
学习新知
随堂练习
作业设计
学
习
新
知
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
——我国古代数学名著
《孙子算经》
鸡兔同笼,有9个头,26条腿。鸡、兔各有几只?
列表法
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
…
…
…
画图法
假如9只全是鸡:
一共有2×9=18条腿
还剩26-18=8条腿
4只兔子
5只鸡
砍腿法
如果每只鸡和兔子都先砍去1条腿,那么一共砍去9条腿。再各砍去1条腿,这时鸡就没有腿了,两轮共砍去18条腿,剩下的腿的数量是兔子的,每只兔子剩2条腿,用8条腿除以2条腿就等于兔子只数。
假设法
(1)假设笼子中全是鸡。
腿共有:2×9=18(条)
比实际少了:26-18=8(条)
1只鸡比1只兔子少了:4-2=2(条)
兔子的只数:8÷2=4(只)
鸡的只数:9-4=5(只)
(2)假设笼子中全是兔子。
腿共有:4×9=36(条)
比实际多了:36-26=10(条)
1只兔子比1只鸡多了:4-2=2(条)
鸡的只数:10÷2=5(只)
兔子的只数:9-5=4(只)
跳跃列表法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只
兔有几只
腿有多少条
判断
1
34
2+34×4=138
×
10
25
20+25×4=120
×
20
15
40+15×4=100
×
23
12
46+12×4=94
√
取中列表法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只
兔有几只
腿有多少条
判断
17
18
34+18×4=106
×
20
15
40+15×4=100
×
23
12
46+12×4=94
√
乐乐的储蓄罐里有1角和5角的硬币共27枚,总共是5.1元,1角和5角的硬币各有多少枚?
1角/枚
5角/枚
总值/元
判断
13
14
1.3+14×0.5=8.3
17
10
1.7+10×0.5=6.7
21
6
2.1+6×0.5=5.1
×
×
√
答:1角的硬币有21枚,5角的硬币有6枚。
返回目录
随堂练习
1.停车场里有三轮车和自行车共22辆,
有59个轮子,自行车、三轮车各几辆?
假设停车场里全是自行车。
三轮车:(59-22×2)÷(3-2)
=(59-44)÷1
=15÷1
=15(辆)
自行车:22-15=7(辆)
答:自行车7辆,三轮车15辆。
2.小明的储蓄罐里有1角和5角的硬币共13枚,
总共是2.1元,1角和5角的硬币各有多少枚?
返回目录
假设储蓄罐里全是1角硬币。
5角硬币:(2.1-13×0.1)÷(0.5-0.1)
=(2.1-1.3)÷0.4
=0.8÷0.4
=2(枚)
1角硬币:13-2=11(枚)
答:1角硬币有11枚,5角硬币有2枚。
作业设计
作业1
作业2
要努力哟!
返回目录
作业1
鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只。
假设笼子里全是鸡。
兔:(88-30×2)÷(4-2)
=(88-60)÷2
=28÷2
=14(只)
鸡:30-14=16(只)
答:鸡有16只,兔有14只。
2.鸡兔同笼,共有头48个,脚132只,求鸡和兔各有
多少只。
假设笼子里全是鸡。
兔:(132-48×2)÷(4-2)
=(132-96)÷2
=36÷2
=18(只)
鸡:48-18=30(只)
答:鸡有30只,兔有18只。
3.
一个饲养组一共养鸡、兔78只,共有200只脚,
求饲养组养鸡和兔各多少只。
返回作业设计
假设笼子里全是鸡。
兔:(200-78×2)÷(4-2)
=(200-156)÷2
=44÷2
=22(只)
鸡:78-22=56(只)
答:鸡有56只,兔有22只。
鸡兔同笼不知数,三十六头笼中露。数清脚共五十双,各有多少鸡和兔?
作业2
假设笼子里全是鸡。
兔:(50×2-36×2)÷(4-2)
=(100-72)÷2
=28÷2
=14(只)
鸡:36-14=22(只)
答:鸡有22只,兔有14只。
2.小明用10元钱正好买了20分和50分的邮票共35张,求这两种邮票各买了多少张。
假设小明买的全是20分的邮票。
50分的邮票:(10-35×0.2)÷(0.5-0.2)
=(10-7)÷0.3
=3÷0.3
=10(张)
20分的邮票:35-10=25(张)
答:20分的邮票买了25张,50分的邮票买了10张。
3.小红用13元6角正好买了50分和80分的邮票共20张,求两种邮票各买了多少张。
假设小红买的全是50分的邮票。
80分的邮票:(13.6-20×0.5)÷(0.8-0.5)
=(13.6-10)÷0.3
=3.6÷0.3
=12(张)
50分的邮票:20-12=8(张)
答:50分的邮票买了8张,80分的邮票买了12张。
返回作业设计
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
