3.3 轴对称与坐标变化 课件(共27张PPT)
文档属性
| 名称 | 3.3 轴对称与坐标变化 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 20:34:18 | ||
图片预览







文档简介
(共27张PPT)
新课导入
你能说出如图所示图案上各个“顶点”的坐标吗?
你还有更简单的方法吗?
3.3
轴对称与坐标变化
学习目标
1.探索图形坐标变化的过程.(重点)
2.掌握图形坐标变化与图形轴对称之间的关系.(难点)
自主发现
(1)两面小旗之间有怎样的位置关系?
关于y轴对称.
(2)写出对应点A、A1及B、B1的坐标,观察有何特点?
纵坐标相同,横坐标互为相反数.
(3)其他对应的点也有这个特点吗?
结论
关于y轴对称的两个点的坐标,它们的纵坐标相同,横坐标互为相反数.
关于x轴对称的两点,坐标有什么特点呢?
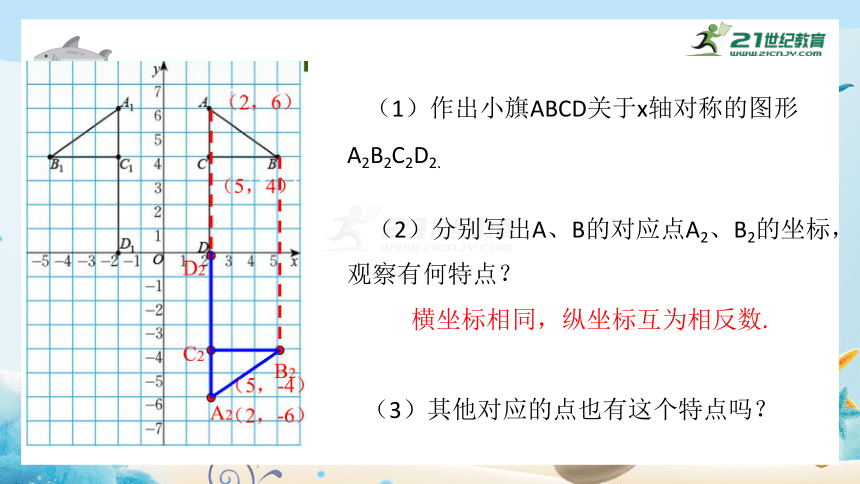
(1)作出小旗ABCD关于x轴对称的图形A2B2C2D2.
(2)分别写出A、B的对应点A2、B2的坐标,观察有何特点?
横坐标相同,纵坐标互为相反数.
(3)其他对应的点也有这个特点吗?
结论
关于x轴对称的两个点的坐标,它们的横坐标相同,纵坐标互为相反数.
结论
关于y轴对称的两个点的坐标,它们的纵坐标相同,横坐标互为相反数.
关于x轴对称的两个点的坐标,它们的横坐标相同,纵坐标互为相反数.
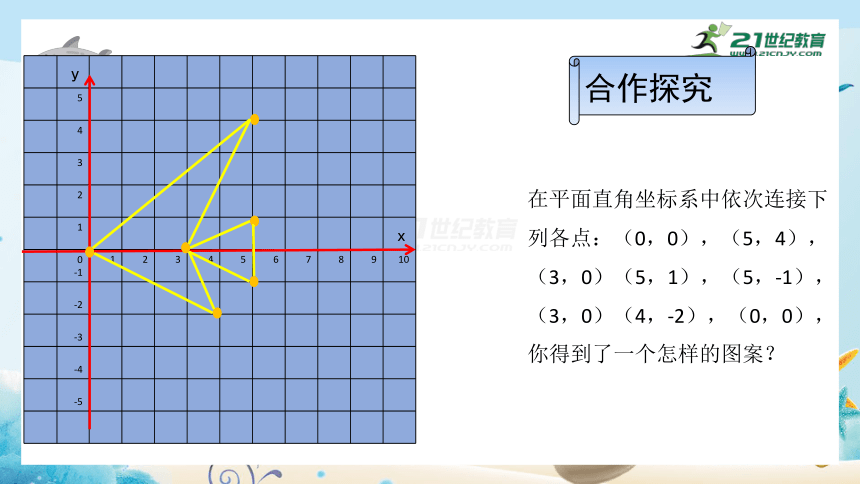
合作探究
5
4
3
2
1
0
-1
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
x
y
在平面直角坐标系中依次连接下列各点:(0,0),(5,4),(3,0)(5,1),(5,-1),(3,0)(4,-2),(0,0),你得到了一个怎样的图案?
5
4
3
2
1
-5
-4
-3
-2
-1
0
-1
1
2
3
4
5
-2
-3
-4
-5
将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
x
y
两个图案关于y轴对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-x,y)
(0,0)
(-5,4)
(-3,0)
(-5,1)
(-5,-1)
(-3,0)
(-4,-2)
(0,0)
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
合作探究
5
4
3
2
1
0
-1
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
x
y
将原图案的各“顶点”的横坐标保持不变,纵坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
两个图案关于x轴对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(x,-y)
(0,0)
(5,-4)
(3,0)
(5,-1)
(5,1)
(3,0)
(4,2)
(0,0)
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
2、关于x轴对称的两个图形上点的坐标特征:
(x,y)→(x,-y)
1.点A(2,-3)关于y轴对称的点的坐标是
.
2.点A(-2,-5)关于x轴对称的点的坐标是
.
3.已知点A的坐标为(-7,2),点B的坐标为(-7,-2),则点A与点B关于
对称.
4.已知点A的坐标为(8,-6),点B的坐标为(-8,-6),则点A与点B关于
对称.
5.点(m,-1)和点(2,n)关于x轴对称,则mn等于
.
(-2,-3)
(-2,5)
x轴
y轴
2
5
4
3
2
1
-5
-4
-3
-2
-1
0
-1
1
2
3
4
5
-2
-3
-4
-5
将所得图案的各个“顶点”的纵坐标保持不变,横、纵坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
x
y
两个图案关于原点对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-x,-y)
(0,0)
(-5,-4)
(-3,0)
(-5,-1)
(-5,1)
(-3,0)
(-4,2)
(0,0)
猜想
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
2、关于x轴对称的两个图形上点的坐标特征:
(x,y)→(x,-y)
3、关于原点对称的两个图形上点的坐标特征:
(x,y)→(-x,-y)
你能尽快说出如图所示图案上各个“顶点”的坐标吗?
归纳总结
1.关于y轴对称的两个图形上点的坐标特征:
(x
,
y)
(-x
,
y)
2.关于x轴对称的两个图形上点的坐标特征:
(x
,
y)
(x
,
-y)
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于
________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于
______成轴对称.
x轴
y轴
想一想
1.点A(2,-
3)关于x轴对称的点的坐标是
.
2.点B(
-
2,1)关于y轴对称的点的坐标是
.
3.点(4,3)与点(4,-
3)的关系是(
)
A.关于原点对称
B.关于
x轴对称
C.关于
y轴对称
D.不能构成对称关系
4.点(m,-
1)和点(2,n)关于x轴对称,
则m
n等于(
)
A.-
2
B.2
C.1
D.-
1
(2,3)
(2,1)
B
B
当堂练习
5.
已知A、B两点的坐标分别是(-2,3)和(2,3),
则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
6.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是(
)
A.4
B.5
C.6
D.7
B
B
7.点P到x轴的距离是2.5;到y轴的距离是4.5.
求点P的坐标.
(4.5,2.5)或(-4.5,2.5)或(-4.5,-2.5)或(4.5,-2.5)
(1)点A的坐标为
,点B的坐标为
;
(2)在x轴上有一条河,现准备在河流边上建一个抽水站P,使得抽水站P到A、B两个村庄的距离之和最小,请作出点P的位置,并求此时距离之和的最小值.
已知:A,B两个村庄在如图所示的直角坐标系中,那么:
拓展提升:
作出点B关于x轴的对称点B1,连接AB1,与x轴的交点就是抽水站P的位置,理由如下:
连接PB,则PB=PB1,有AP+PB=AB+PB1;
根据两点之间线段最短知:AP+PB的最小值即为线段AB1的长度。于是,问题转化为求线段AB1的长度.
分别过点A、B1作x轴、y轴的垂线,交点为C,得到Rt△AB1C.
显然AC=3,B1C=4,根据勾股定理可得AB1=5.
于是,AP+PB的最小值为5.
课堂总结
轴对称与坐标变换
关于坐标轴对称
作图——关于轴对称变化
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
新课导入
你能说出如图所示图案上各个“顶点”的坐标吗?
你还有更简单的方法吗?
3.3
轴对称与坐标变化
学习目标
1.探索图形坐标变化的过程.(重点)
2.掌握图形坐标变化与图形轴对称之间的关系.(难点)
自主发现
(1)两面小旗之间有怎样的位置关系?
关于y轴对称.
(2)写出对应点A、A1及B、B1的坐标,观察有何特点?
纵坐标相同,横坐标互为相反数.
(3)其他对应的点也有这个特点吗?
结论
关于y轴对称的两个点的坐标,它们的纵坐标相同,横坐标互为相反数.
关于x轴对称的两点,坐标有什么特点呢?
(1)作出小旗ABCD关于x轴对称的图形A2B2C2D2.
(2)分别写出A、B的对应点A2、B2的坐标,观察有何特点?
横坐标相同,纵坐标互为相反数.
(3)其他对应的点也有这个特点吗?
结论
关于x轴对称的两个点的坐标,它们的横坐标相同,纵坐标互为相反数.
结论
关于y轴对称的两个点的坐标,它们的纵坐标相同,横坐标互为相反数.
关于x轴对称的两个点的坐标,它们的横坐标相同,纵坐标互为相反数.
合作探究
5
4
3
2
1
0
-1
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
x
y
在平面直角坐标系中依次连接下列各点:(0,0),(5,4),(3,0)(5,1),(5,-1),(3,0)(4,-2),(0,0),你得到了一个怎样的图案?
5
4
3
2
1
-5
-4
-3
-2
-1
0
-1
1
2
3
4
5
-2
-3
-4
-5
将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
x
y
两个图案关于y轴对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-x,y)
(0,0)
(-5,4)
(-3,0)
(-5,1)
(-5,-1)
(-3,0)
(-4,-2)
(0,0)
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
合作探究
5
4
3
2
1
0
-1
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
x
y
将原图案的各“顶点”的横坐标保持不变,纵坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
两个图案关于x轴对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(x,-y)
(0,0)
(5,-4)
(3,0)
(5,-1)
(5,1)
(3,0)
(4,2)
(0,0)
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
2、关于x轴对称的两个图形上点的坐标特征:
(x,y)→(x,-y)
1.点A(2,-3)关于y轴对称的点的坐标是
.
2.点A(-2,-5)关于x轴对称的点的坐标是
.
3.已知点A的坐标为(-7,2),点B的坐标为(-7,-2),则点A与点B关于
对称.
4.已知点A的坐标为(8,-6),点B的坐标为(-8,-6),则点A与点B关于
对称.
5.点(m,-1)和点(2,n)关于x轴对称,则mn等于
.
(-2,-3)
(-2,5)
x轴
y轴
2
5
4
3
2
1
-5
-4
-3
-2
-1
0
-1
1
2
3
4
5
-2
-3
-4
-5
将所得图案的各个“顶点”的纵坐标保持不变,横、纵坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案有怎样的位置关系呢?
x
y
两个图案关于原点对称
顶点坐标变化为:
(x,y)
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-x,-y)
(0,0)
(-5,-4)
(-3,0)
(-5,-1)
(-5,1)
(-3,0)
(-4,2)
(0,0)
猜想
1、关于y轴对称的两个图形上点的坐标特征:
(x,y)→(-x,y)
2、关于x轴对称的两个图形上点的坐标特征:
(x,y)→(x,-y)
3、关于原点对称的两个图形上点的坐标特征:
(x,y)→(-x,-y)
你能尽快说出如图所示图案上各个“顶点”的坐标吗?
归纳总结
1.关于y轴对称的两个图形上点的坐标特征:
(x
,
y)
(-x
,
y)
2.关于x轴对称的两个图形上点的坐标特征:
(x
,
y)
(x
,
-y)
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于
________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于
______成轴对称.
x轴
y轴
想一想
1.点A(2,-
3)关于x轴对称的点的坐标是
.
2.点B(
-
2,1)关于y轴对称的点的坐标是
.
3.点(4,3)与点(4,-
3)的关系是(
)
A.关于原点对称
B.关于
x轴对称
C.关于
y轴对称
D.不能构成对称关系
4.点(m,-
1)和点(2,n)关于x轴对称,
则m
n等于(
)
A.-
2
B.2
C.1
D.-
1
(2,3)
(2,1)
B
B
当堂练习
5.
已知A、B两点的坐标分别是(-2,3)和(2,3),
则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
6.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是(
)
A.4
B.5
C.6
D.7
B
B
7.点P到x轴的距离是2.5;到y轴的距离是4.5.
求点P的坐标.
(4.5,2.5)或(-4.5,2.5)或(-4.5,-2.5)或(4.5,-2.5)
(1)点A的坐标为
,点B的坐标为
;
(2)在x轴上有一条河,现准备在河流边上建一个抽水站P,使得抽水站P到A、B两个村庄的距离之和最小,请作出点P的位置,并求此时距离之和的最小值.
已知:A,B两个村庄在如图所示的直角坐标系中,那么:
拓展提升:
作出点B关于x轴的对称点B1,连接AB1,与x轴的交点就是抽水站P的位置,理由如下:
连接PB,则PB=PB1,有AP+PB=AB+PB1;
根据两点之间线段最短知:AP+PB的最小值即为线段AB1的长度。于是,问题转化为求线段AB1的长度.
分别过点A、B1作x轴、y轴的垂线,交点为C,得到Rt△AB1C.
显然AC=3,B1C=4,根据勾股定理可得AB1=5.
于是,AP+PB的最小值为5.
课堂总结
轴对称与坐标变换
关于坐标轴对称
作图——关于轴对称变化
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
