12.1-12.2 同步练习2021-2022学年八年级数学人教版上册(Word版含答案)
文档属性
| 名称 | 12.1-12.2 同步练习2021-2022学年八年级数学人教版上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 597.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 13:38:55 | ||
图片预览

文档简介
第十二章全等三角形12.1-12.2
同步练习2021-2022学年上学期八年级人教版上册
考试时间:100分钟;满分:120分命题人
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共12题36分)
1.在下列各组图形中,是全等图形的是(
)
A.
B.
C.
D.
2.如图,,若,则的对应角(
)
A.
B.
C.
D.
3.如图,,则等于(
)
A.
B.
C.
D.
4.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47°
B.49°
C.84°
D.96°
5.下列说法中正确的是(
)
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指大小相同的两个三角形
C.全等三角形是指周长相等的两个三角形
D.全等三角形的形状、大小完全相同
6.如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是(
)
A.6cm
B.5cm
C.4cm
D.无法确定
7.如图,在中,D,E分别是边,上的点,若,则的度数为(
)
A.
B.
C.
D.
8.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要测量出AB′的长,就知道AB的长,那么判定△ABC≌△AB′C的理由是(
)
A.
B.
C.
D.
9.如图,,欲证,则补充的条件中不正确的是(
)
A.
B.
C.
D.
10.如图,∠A=∠D,AB=DC,下列条件中,不能使△EAC与△FDB全等的条件是( )
A.
B.
C.
D.
11.如图,,,垂足分别为、,且,则直接判定与全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,在△ABC中,∠ABC=90°,AB=BC,AE是中线,过点B作BF⊥AE于点F,过点C作CD⊥BC交BF的延长线于点D.下列结论:①BE=CE;②AE=BD;③∠BAE=∠CBD;④∠EAC=∠BAE;⑤BC=2CD.正确的个数是( )
A.2个
B.3个
C.4个
D.5个
第II卷(非选择题)
二、填空题(共16分)
13.(本题4分)如图,CD=CB,那么添加条件
能根据SAS判定△ABC≌△ADC.
14.(本题4分)如图,在ABF和DEC中,∠A=∠D,AB=DE,若再添加条件________,则可根据SAS证得ABF
≌DEC.
15.(本题4分)如图,中,,则点B的坐标为________.
16.(本题4分)如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
三、解答题(共68分)
17.(本题10分)如图,已知在中,求证:.
18.(本题10分)如图,,,,.
(1)试说明:;
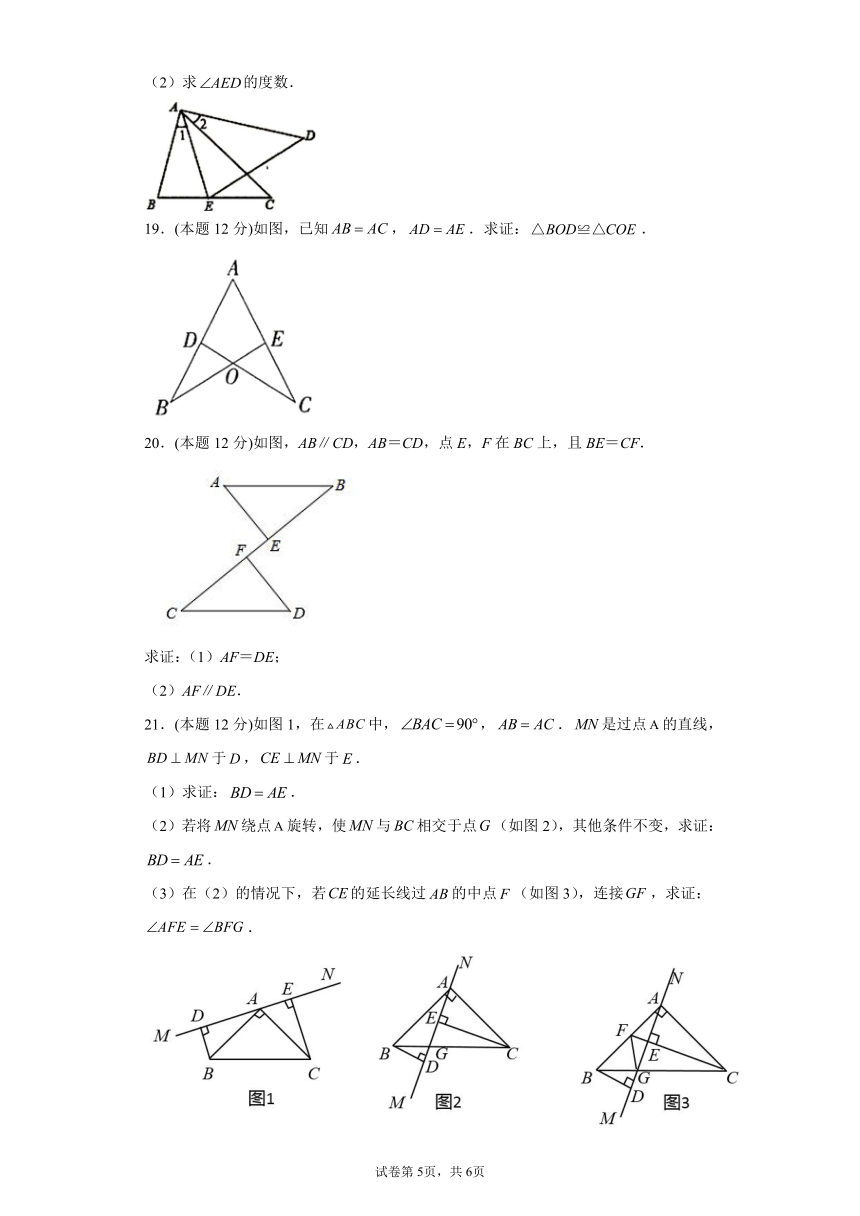
(2)求的度数.
19.(本题12分)如图,已知,.求证:.
20.(本题12分)如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
求证:(1)AF=DE;
(2)AF∥DE.
21.(本题12分)如图1,在中,,.是过点的直线,于,于.
(1)求证:.
(2)若将绕点旋转,使与相交于点(如图2),其他条件不变,求证:.
(3)在(2)的情况下,若的延长线过的中点(如图3),连接,求证:.
22.(本题12分)如图,CE、CB分别是与的中线,且,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.C
3.C
4.C
5.D
6.B
7.D
8.A
9.C
10.A
11.D
12.C
13.∠DCA=∠BCA
【解析】
∵已经知道CD=CB,AC=AC(公共边),
∴要根据“SAS”判定△ABC≌△ADC,需添加的条件是:∠DCA=∠BCA.
14.AF=DC
解:∵∠A=∠D,AB=DE,
若添加AF=DC,可利用SAS证得ABF
≌DEC
故答案为:AF=DC.
15.(4,1)
【详解】
如图,过点B作BD⊥x轴于D,
∵A(0,3),C(1,0),
∴OA=3,OC=1,
∵∠ACB=90°,
∴∠OCA+∠DCB=90°,
∵∠OAC+∠OCA=90°,
∴∠OAC=∠DCB,
在△OAC和△DCB中,,
∴△OAC≌△DCB,
∴BD=OC=1,CD=OA=3,
∴OD=OC+CD=4,
∴点B坐标为(4,1).
故答案为:(4,1)
16.
【详解】
过点作交于点,如图,
,
,
,
,
,
,
,
,
,
(ASA),
,,
,
,
,
,
故答案为:.
17.
【详解】
证明:在和中,
∴.
∴.
又∵,即,
∴,
∴.
18.(1)见解析;(2)60°
【详解】
解:(1)证明:∵,
∴,即.
∵在和中,
,
∴.
(2)由(1)证得,
∵
∴.
19.见解析
解析:本题主要考查全等三角形的判定和性质,要证明三角形全等,需要先从三角形中确定相等的对应元素,再根据相等的对应元素选择合适的方法进行证明.
答案:证明:在和中,
∴(SAS).
∴,∵,,
∴,即.
在和中,
20.
【详解】
证明:∵BE=CF,
∴BE-EF=CF-EF,
∴BF=CE.
∵AB∥CD,
∴∠B=∠C.
在△ABF和△DCE中
∵,
∴△ABF≌△DCE(SAS),
∴AF=DE;
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
21.
解:(1)∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB
+∠EAC=90°,
∴∠DBA=∠EAC,
∵AB
=
AC,
∴△ADB≌△CEA(AAS),
∴BD=AE;
(2)∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB
+∠EAC=90°,
∴∠DBA=∠EAC,
∵AB
=
AC,
∴△ADB≌△CEA(AAS),
∴BD=AE,
(3)过B作BP//AC交MN于P,如图所示
∵BP//AC,
∴∠PBA+∠BAC=90°,
∵∠BAC=90°,
∴∠PBA=∠BAC=90°
由(2)得:△ADB≌△CEA,
∴∠BAP=∠ACF,
∵AB=AC,
∴△ACF≌△ABP(ASA),
∴∠1=∠3,
∴AF=BP,
∵AB的中点F,
∵BF=AF,
∴BF=BP,
∵∠ABC=45°,
又∵∠PBA=90°,
∴∠PBG=∠PBA-∠ABC
=45°,
∴∠ABC=∠PBG,
∵BG=BG,
∴△BFG≌△BPG(SAS),
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2即∠AFE=∠BFG.
22.
解析:过点B作交CE的延长线于点F,由点E为AB中点,得到,再由BF与AC平行,得到两对内错角相等,利用AAS得到与全等,利用全等三角形的对应边相等得到,,即,再由,根据点B为AD中点,得到,利用外角性质及等量代换得到,利用SAS得到与全等,利用全等三角形对应边相等得到,等量代换即可得证.
答案:证明:如图,过点B作交CE的延长线于点F.
∵CE是的中线,,
∴,,,
在和中,
∵
∴(AAS),
∴,,
∴,
又∵,CB是的中线,
∴,
∵,
∵,
∴,
在和中,
∵
∴(SAS),
∴.
易错:证明:在和中,
∴(ASA)..答案第1页,共2页
答案第1页,共2页
同步练习2021-2022学年上学期八年级人教版上册
考试时间:100分钟;满分:120分命题人
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共12题36分)
1.在下列各组图形中,是全等图形的是(
)
A.
B.
C.
D.
2.如图,,若,则的对应角(
)
A.
B.
C.
D.
3.如图,,则等于(
)
A.
B.
C.
D.
4.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47°
B.49°
C.84°
D.96°
5.下列说法中正确的是(
)
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指大小相同的两个三角形
C.全等三角形是指周长相等的两个三角形
D.全等三角形的形状、大小完全相同
6.如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是(
)
A.6cm
B.5cm
C.4cm
D.无法确定
7.如图,在中,D,E分别是边,上的点,若,则的度数为(
)
A.
B.
C.
D.
8.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要测量出AB′的长,就知道AB的长,那么判定△ABC≌△AB′C的理由是(
)
A.
B.
C.
D.
9.如图,,欲证,则补充的条件中不正确的是(
)
A.
B.
C.
D.
10.如图,∠A=∠D,AB=DC,下列条件中,不能使△EAC与△FDB全等的条件是( )
A.
B.
C.
D.
11.如图,,,垂足分别为、,且,则直接判定与全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,在△ABC中,∠ABC=90°,AB=BC,AE是中线,过点B作BF⊥AE于点F,过点C作CD⊥BC交BF的延长线于点D.下列结论:①BE=CE;②AE=BD;③∠BAE=∠CBD;④∠EAC=∠BAE;⑤BC=2CD.正确的个数是( )
A.2个
B.3个
C.4个
D.5个
第II卷(非选择题)
二、填空题(共16分)
13.(本题4分)如图,CD=CB,那么添加条件
能根据SAS判定△ABC≌△ADC.
14.(本题4分)如图,在ABF和DEC中,∠A=∠D,AB=DE,若再添加条件________,则可根据SAS证得ABF
≌DEC.
15.(本题4分)如图,中,,则点B的坐标为________.
16.(本题4分)如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
三、解答题(共68分)
17.(本题10分)如图,已知在中,求证:.
18.(本题10分)如图,,,,.
(1)试说明:;
(2)求的度数.
19.(本题12分)如图,已知,.求证:.
20.(本题12分)如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
求证:(1)AF=DE;
(2)AF∥DE.
21.(本题12分)如图1,在中,,.是过点的直线,于,于.
(1)求证:.
(2)若将绕点旋转,使与相交于点(如图2),其他条件不变,求证:.
(3)在(2)的情况下,若的延长线过的中点(如图3),连接,求证:.
22.(本题12分)如图,CE、CB分别是与的中线,且,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.C
3.C
4.C
5.D
6.B
7.D
8.A
9.C
10.A
11.D
12.C
13.∠DCA=∠BCA
【解析】
∵已经知道CD=CB,AC=AC(公共边),
∴要根据“SAS”判定△ABC≌△ADC,需添加的条件是:∠DCA=∠BCA.
14.AF=DC
解:∵∠A=∠D,AB=DE,
若添加AF=DC,可利用SAS证得ABF
≌DEC
故答案为:AF=DC.
15.(4,1)
【详解】
如图,过点B作BD⊥x轴于D,
∵A(0,3),C(1,0),
∴OA=3,OC=1,
∵∠ACB=90°,
∴∠OCA+∠DCB=90°,
∵∠OAC+∠OCA=90°,
∴∠OAC=∠DCB,
在△OAC和△DCB中,,
∴△OAC≌△DCB,
∴BD=OC=1,CD=OA=3,
∴OD=OC+CD=4,
∴点B坐标为(4,1).
故答案为:(4,1)
16.
【详解】
过点作交于点,如图,
,
,
,
,
,
,
,
,
,
(ASA),
,,
,
,
,
,
故答案为:.
17.
【详解】
证明:在和中,
∴.
∴.
又∵,即,
∴,
∴.
18.(1)见解析;(2)60°
【详解】
解:(1)证明:∵,
∴,即.
∵在和中,
,
∴.
(2)由(1)证得,
∵
∴.
19.见解析
解析:本题主要考查全等三角形的判定和性质,要证明三角形全等,需要先从三角形中确定相等的对应元素,再根据相等的对应元素选择合适的方法进行证明.
答案:证明:在和中,
∴(SAS).
∴,∵,,
∴,即.
在和中,
20.
【详解】
证明:∵BE=CF,
∴BE-EF=CF-EF,
∴BF=CE.
∵AB∥CD,
∴∠B=∠C.
在△ABF和△DCE中
∵,
∴△ABF≌△DCE(SAS),
∴AF=DE;
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
21.
解:(1)∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB
+∠EAC=90°,
∴∠DBA=∠EAC,
∵AB
=
AC,
∴△ADB≌△CEA(AAS),
∴BD=AE;
(2)∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB
+∠EAC=90°,
∴∠DBA=∠EAC,
∵AB
=
AC,
∴△ADB≌△CEA(AAS),
∴BD=AE,
(3)过B作BP//AC交MN于P,如图所示
∵BP//AC,
∴∠PBA+∠BAC=90°,
∵∠BAC=90°,
∴∠PBA=∠BAC=90°
由(2)得:△ADB≌△CEA,
∴∠BAP=∠ACF,
∵AB=AC,
∴△ACF≌△ABP(ASA),
∴∠1=∠3,
∴AF=BP,
∵AB的中点F,
∵BF=AF,
∴BF=BP,
∵∠ABC=45°,
又∵∠PBA=90°,
∴∠PBG=∠PBA-∠ABC
=45°,
∴∠ABC=∠PBG,
∵BG=BG,
∴△BFG≌△BPG(SAS),
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2即∠AFE=∠BFG.
22.
解析:过点B作交CE的延长线于点F,由点E为AB中点,得到,再由BF与AC平行,得到两对内错角相等,利用AAS得到与全等,利用全等三角形的对应边相等得到,,即,再由,根据点B为AD中点,得到,利用外角性质及等量代换得到,利用SAS得到与全等,利用全等三角形对应边相等得到,等量代换即可得证.
答案:证明:如图,过点B作交CE的延长线于点F.
∵CE是的中线,,
∴,,,
在和中,
∵
∴(AAS),
∴,,
∴,
又∵,CB是的中线,
∴,
∵,
∵,
∴,
在和中,
∵
∴(SAS),
∴.
易错:证明:在和中,
∴(ASA)..答案第1页,共2页
答案第1页,共2页
