二次函数中有关平行四边形四边形的存在性问题
文档属性
| 名称 | 二次函数中有关平行四边形四边形的存在性问题 | 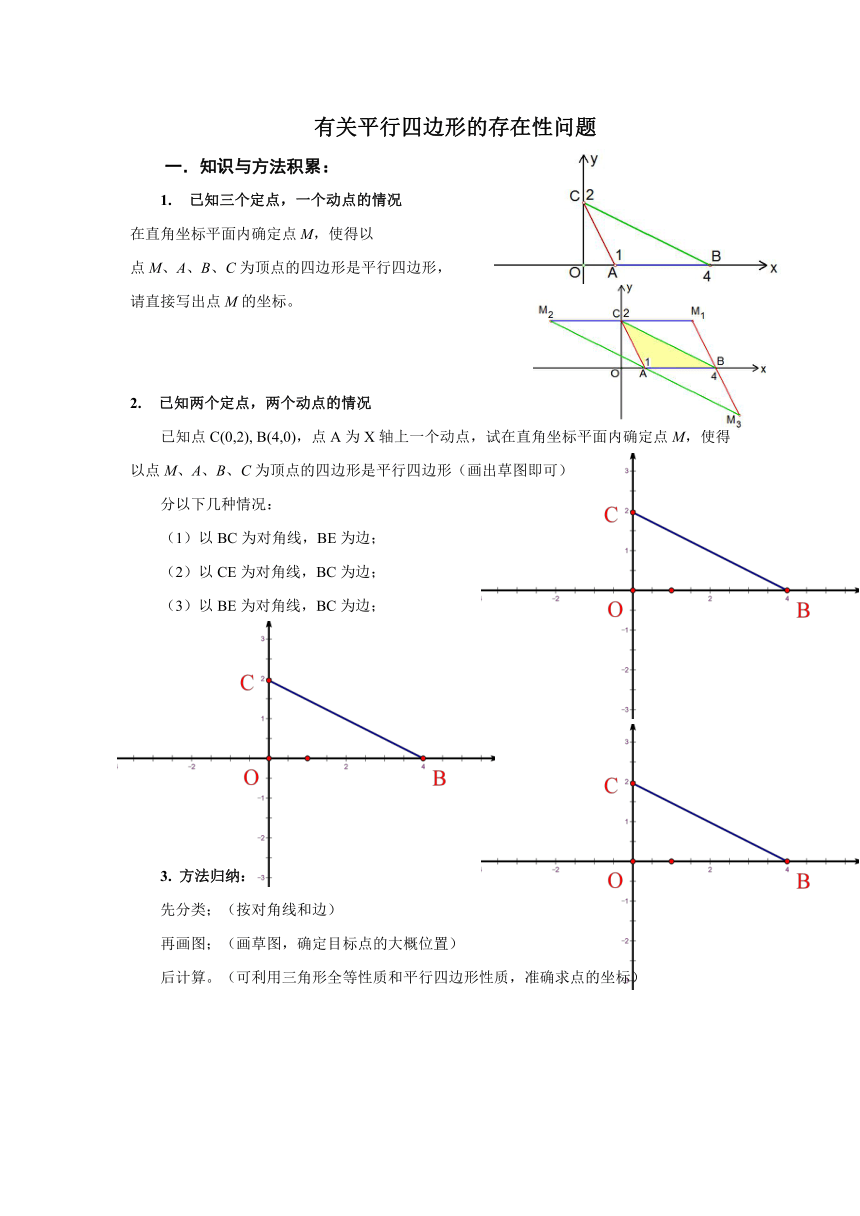 | |
| 格式 | zip | ||
| 文件大小 | 360.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-16 12:17:56 | ||
图片预览


文档简介
有关平行四边形的存在性问题
一.知识与方法积累:
1. 已知三个定点,一个动点的情况
在直角坐标平面内确定点M,使得以
点M、A、B、C为顶点的四边形是平行四边形,
请直接写出点M的坐标。
2. 已知两个定点,两个动点的情况
已知点C(0,2), B(4,0),点A为X轴上一个动点,试在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形(画出草图即可)
分以下几种情况:
(1)以BC为对角线,BE为边;
(2)以CE为对角线,BC为边;
(3)以BE为对角线,BC为边;
3. 方法归纳:
先分类;(按对角线和边)
再画图;(画草图,确定目标点的大概位置)
后计算。(可利用三角形全等性质和平行四边形性质,准确求点的坐标)
二.例题解析:
如图,抛物线与轴交于点C,与轴交于A、B两点,,.
(1)求点B的坐标; (2)求抛物线的解析式及顶点坐标;
(3)设点E在轴上,点F在抛物线上,如果A、C、E、F构成平行四边形,请求出点E的坐标.
巩固练习:
1. 已知抛物线与轴的一个交点为 A(-1,0),与y轴的正半轴交于点C. 问坐标平面内是否存在点,使得以点M和抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2. 若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点E在y轴上,写出点P的坐标.
3.如图,抛物线与轴相交于、两点(点在点的左侧),与 轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;并求出当为何值时,四边形为平行四边形?
4. 已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
5.如图,已知抛物线的顶点坐标为Q,且与轴交于点C,与轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
6. 如图,抛物线与轴交于两点A(-1,0),B(1,0),与轴交于点C.
(1)求抛物线的解析式;( )
(2)过点B作BD∥CA与抛物线交于点D,求四边形ACBD的面积;
四边形ACBD的面积=AB OC +AB DE
(也可直接求直角梯形ACBD的面积为4)
(3)在轴下方的抛物线上是否存在一点M,过M作MN⊥轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.
C
A
B
O
y
x
一.知识与方法积累:
1. 已知三个定点,一个动点的情况
在直角坐标平面内确定点M,使得以
点M、A、B、C为顶点的四边形是平行四边形,
请直接写出点M的坐标。
2. 已知两个定点,两个动点的情况
已知点C(0,2), B(4,0),点A为X轴上一个动点,试在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形(画出草图即可)
分以下几种情况:
(1)以BC为对角线,BE为边;
(2)以CE为对角线,BC为边;
(3)以BE为对角线,BC为边;
3. 方法归纳:
先分类;(按对角线和边)
再画图;(画草图,确定目标点的大概位置)
后计算。(可利用三角形全等性质和平行四边形性质,准确求点的坐标)
二.例题解析:
如图,抛物线与轴交于点C,与轴交于A、B两点,,.
(1)求点B的坐标; (2)求抛物线的解析式及顶点坐标;
(3)设点E在轴上,点F在抛物线上,如果A、C、E、F构成平行四边形,请求出点E的坐标.
巩固练习:
1. 已知抛物线与轴的一个交点为 A(-1,0),与y轴的正半轴交于点C. 问坐标平面内是否存在点,使得以点M和抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2. 若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点E在y轴上,写出点P的坐标.
3.如图,抛物线与轴相交于、两点(点在点的左侧),与 轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;并求出当为何值时,四边形为平行四边形?
4. 已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
5.如图,已知抛物线的顶点坐标为Q,且与轴交于点C,与轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
6. 如图,抛物线与轴交于两点A(-1,0),B(1,0),与轴交于点C.
(1)求抛物线的解析式;( )
(2)过点B作BD∥CA与抛物线交于点D,求四边形ACBD的面积;
四边形ACBD的面积=AB OC +AB DE
(也可直接求直角梯形ACBD的面积为4)
(3)在轴下方的抛物线上是否存在一点M,过M作MN⊥轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.
C
A
B
O
y
x
