2021-2022学年华东师大版数学九年级上册23.3 相似三角形 第1 课时 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册23.3 相似三角形 第1 课时 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 19:55:30 | ||
图片预览



文档简介
(共19张PPT)
23.3
相似三角形
第1课时
相似三角形
(华东师大版)2021-2022年度九年级数学上期
问题1
相似多边形的主要特征是什么?
导入新课
回顾与思考
问题2
相似比的定义是什么?
相似多边形的对应边成比例,对应角相等。
相似比就是对应边的比。
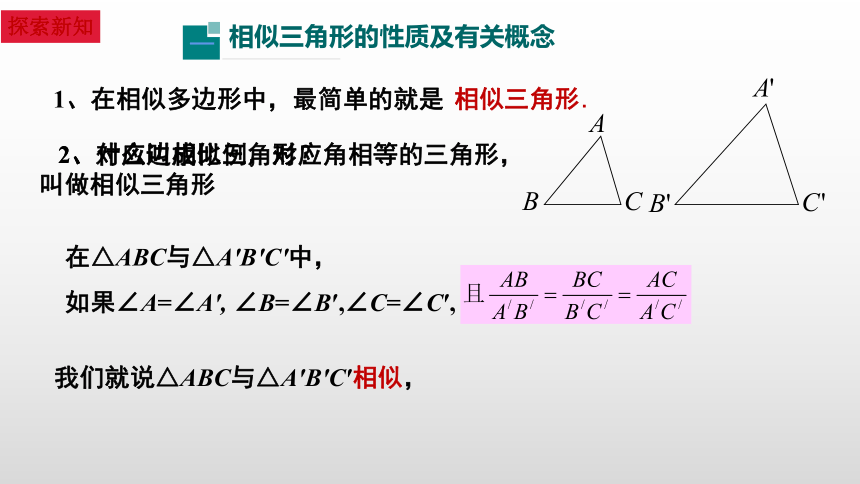
我们就说△ABC与△A′B′C′相似,
1、在相似多边形中,最简单的就是
探索新知
相似三角形的性质及有关概念
一
在△ABC与△A′B′C′中,
如果∠A=∠A′,
∠B=∠B′,∠C=∠C′,
相似三角形.
2、什么叫相似三角形?
2、对应边成比例,对应角相等的三角形,
叫做相似三角形
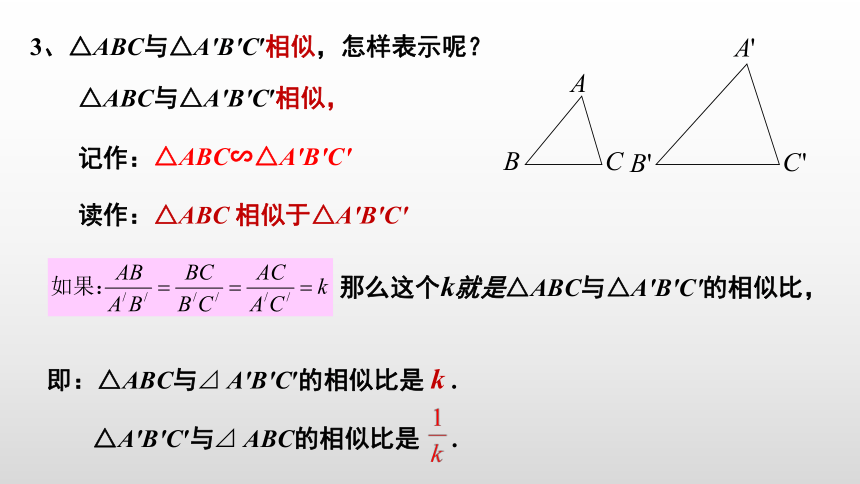
3、△ABC与△A′B′C′相似,怎样表示呢?
△ABC与△A′B′C′相似,
记作:
△ABC∽△A′B′C′
读作:△ABC
相似于△A′B′C′
那么这个k就是△ABC与△A′B′C′的相似比,
即:△ABC与⊿
A′B′C′的相似比是
k
.
△A′B′C′与⊿
ABC的相似比是
.
∵△ABC∽△A′B′C′,
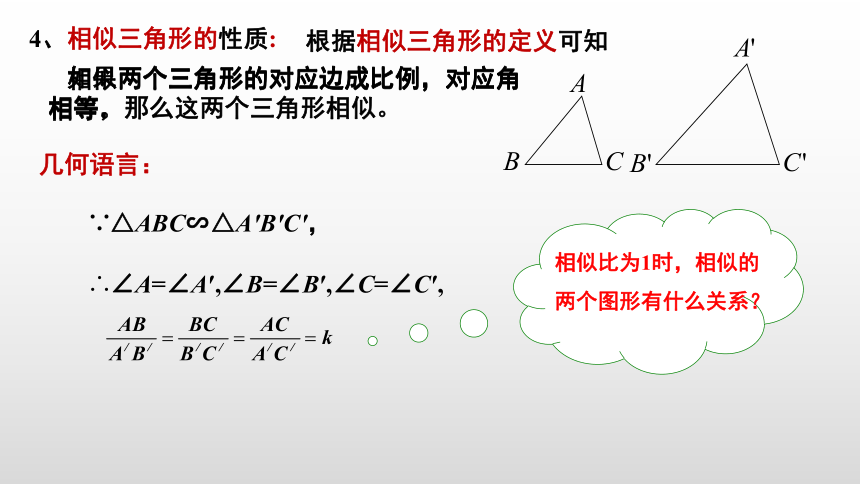
相似比为1时,相似的
两个图形有什么关系?
4、相似三角形的性质:
如果两个三角形的对应边成比例,对应角相等,那么这两个三角形相似。
根据相似三角形的定义可知
相似两个三角形的对应边成比例,对应角相等。
几何语言:
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
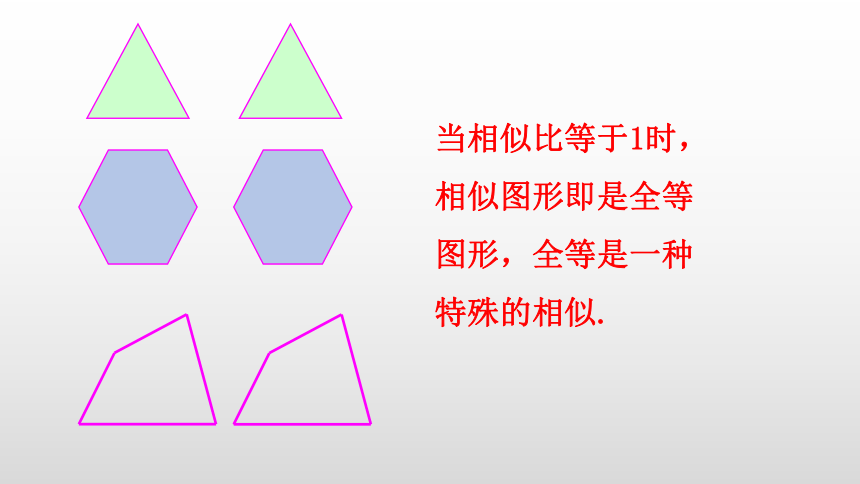
当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似.
应用
例1、已知⊿ABC的三边分别为20㎝、50㎝、60㎝。现要利用长度分别
为30㎝和60㎝的细木条各一根,做一个三角形与⊿ABC相似,要求:以
其中一根为边,另一根截成两段(允许有余料)作为另两边。求另两边
长。
解:
设将60㎝的细木条分成两段作的另两边长分别为
㎝和
㎝。
∵
所做的三角形与⊿ABC相似
∴
①、若30㎝为最长边,
分3种情况
则
,
解得:
②、若30㎝为较长边,
则
,
解得:
③、若30㎝为最短边,
则
,
解得:
不合题意,舍去
跟进练习
1、小明做两个形状相同的三角形框架,其中一个框架的三边分别为30㎝、
40㎝、50㎝,另一个三角形框架现在只有一条60㎝的木条,小明应该再
两根多长的木条?
2、如果一个直角三角形的两条边分别为6和8,与它相似的另一个三角形的三边分别是3、4和
,则
的值是
如图,DE//BC,
△ADE与△ABC有什么关系?说明理由.
A
B
C
D
解:相似,在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,∠AED=∠C,
过E作EF//AB交BC于F
F
E
由平行线判定两个三角形相似
二
探究归纳
∴四边形BDEF是平行四边形,
∴DE=BF
∴△ADE∽△ABC
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
“A”型
“X”型
(图2)
D
E
A
B
C
A
B
C
D
E
(图1)
归纳
平行线分得的三角形与原三角形相似
简言之
几何语言:
∵
DE//BC,
∴⊿ADE∽⊿ABC
∵
DE//BC,
∴⊿ADE∽⊿ACB
例2、
如图,在⊿ABC中,点D是边AB的三等分点,DE//BC,DE=5,求BC的长。
A
B
C
D
E
解:
∵
DE//BC,
∴⊿ADE∽⊿ABC
∵在⊿ABC中,点D是边AB的三等分点
1.如果两个三角形的相似比为1,那么这两个三角形_____.
2.若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=
4
cm,那么△A′B′C′与△ABC的相似比是____
.
3.若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么△
A′B′C′的最大边长是_____.
全等
4︰3
24cm
当堂练习
4.若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
5.把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,
下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
C
C
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
课堂小结
1.相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
拓展
1、如图在
ABCD中,G为BC延长线上一点,AG与AD交于点E,于
DC交于点F,则相似三角形有
个,分别是
。
2、如图P为
中,斜边AB上任意一点,过点P做一条直线,使截得的
三角形与
相似,这样的直线可以做
条。
3、已知在
中,AB=7,AC=8,E是AB上任意一点,且AE:AB=3:5,
F为AC上一点,且
与原三角形相似,则AF=
。
4、如图在
ABCD中,E为AB上一点,CE与BD交于点F,若AE:BE=4:3,
且BF=2,则DF=
。
5、已知如图AB//GH//CD,点H在BC上,AC与BD交于点G,AB=2,CD=3.
则GH=
。
6、在梯形ABCD中,AD//BC,E为AD的中点,连结BE交AC于点F,BE的
延长线交CD于点G。(1)、求证:
(2)、若GE=2,EF=3,求EF的长。
7、如图,在平面直角坐标系中,OA=12,OB=6,点P从点O开始沿OA边,向
点A以1㎝/s的速度移动。如果P、Q同时出发,用t秒表示移动时间。
①、写出⊿POQ的面积y与时间t的函数关系,并求出是t在取值范围。
②、当t为何值时,⊿POQ与⊿AOB相似。
23.3
相似三角形
第1课时
相似三角形
(华东师大版)2021-2022年度九年级数学上期
问题1
相似多边形的主要特征是什么?
导入新课
回顾与思考
问题2
相似比的定义是什么?
相似多边形的对应边成比例,对应角相等。
相似比就是对应边的比。
我们就说△ABC与△A′B′C′相似,
1、在相似多边形中,最简单的就是
探索新知
相似三角形的性质及有关概念
一
在△ABC与△A′B′C′中,
如果∠A=∠A′,
∠B=∠B′,∠C=∠C′,
相似三角形.
2、什么叫相似三角形?
2、对应边成比例,对应角相等的三角形,
叫做相似三角形
3、△ABC与△A′B′C′相似,怎样表示呢?
△ABC与△A′B′C′相似,
记作:
△ABC∽△A′B′C′
读作:△ABC
相似于△A′B′C′
那么这个k就是△ABC与△A′B′C′的相似比,
即:△ABC与⊿
A′B′C′的相似比是
k
.
△A′B′C′与⊿
ABC的相似比是
.
∵△ABC∽△A′B′C′,
相似比为1时,相似的
两个图形有什么关系?
4、相似三角形的性质:
如果两个三角形的对应边成比例,对应角相等,那么这两个三角形相似。
根据相似三角形的定义可知
相似两个三角形的对应边成比例,对应角相等。
几何语言:
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似.
应用
例1、已知⊿ABC的三边分别为20㎝、50㎝、60㎝。现要利用长度分别
为30㎝和60㎝的细木条各一根,做一个三角形与⊿ABC相似,要求:以
其中一根为边,另一根截成两段(允许有余料)作为另两边。求另两边
长。
解:
设将60㎝的细木条分成两段作的另两边长分别为
㎝和
㎝。
∵
所做的三角形与⊿ABC相似
∴
①、若30㎝为最长边,
分3种情况
则
,
解得:
②、若30㎝为较长边,
则
,
解得:
③、若30㎝为最短边,
则
,
解得:
不合题意,舍去
跟进练习
1、小明做两个形状相同的三角形框架,其中一个框架的三边分别为30㎝、
40㎝、50㎝,另一个三角形框架现在只有一条60㎝的木条,小明应该再
两根多长的木条?
2、如果一个直角三角形的两条边分别为6和8,与它相似的另一个三角形的三边分别是3、4和
,则
的值是
如图,DE//BC,
△ADE与△ABC有什么关系?说明理由.
A
B
C
D
解:相似,在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,∠AED=∠C,
过E作EF//AB交BC于F
F
E
由平行线判定两个三角形相似
二
探究归纳
∴四边形BDEF是平行四边形,
∴DE=BF
∴△ADE∽△ABC
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
“A”型
“X”型
(图2)
D
E
A
B
C
A
B
C
D
E
(图1)
归纳
平行线分得的三角形与原三角形相似
简言之
几何语言:
∵
DE//BC,
∴⊿ADE∽⊿ABC
∵
DE//BC,
∴⊿ADE∽⊿ACB
例2、
如图,在⊿ABC中,点D是边AB的三等分点,DE//BC,DE=5,求BC的长。
A
B
C
D
E
解:
∵
DE//BC,
∴⊿ADE∽⊿ABC
∵在⊿ABC中,点D是边AB的三等分点
1.如果两个三角形的相似比为1,那么这两个三角形_____.
2.若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=
4
cm,那么△A′B′C′与△ABC的相似比是____
.
3.若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么△
A′B′C′的最大边长是_____.
全等
4︰3
24cm
当堂练习
4.若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
5.把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,
下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
C
C
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
课堂小结
1.相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
拓展
1、如图在
ABCD中,G为BC延长线上一点,AG与AD交于点E,于
DC交于点F,则相似三角形有
个,分别是
。
2、如图P为
中,斜边AB上任意一点,过点P做一条直线,使截得的
三角形与
相似,这样的直线可以做
条。
3、已知在
中,AB=7,AC=8,E是AB上任意一点,且AE:AB=3:5,
F为AC上一点,且
与原三角形相似,则AF=
。
4、如图在
ABCD中,E为AB上一点,CE与BD交于点F,若AE:BE=4:3,
且BF=2,则DF=
。
5、已知如图AB//GH//CD,点H在BC上,AC与BD交于点G,AB=2,CD=3.
则GH=
。
6、在梯形ABCD中,AD//BC,E为AD的中点,连结BE交AC于点F,BE的
延长线交CD于点G。(1)、求证:
(2)、若GE=2,EF=3,求EF的长。
7、如图,在平面直角坐标系中,OA=12,OB=6,点P从点O开始沿OA边,向
点A以1㎝/s的速度移动。如果P、Q同时出发,用t秒表示移动时间。
①、写出⊿POQ的面积y与时间t的函数关系,并求出是t在取值范围。
②、当t为何值时,⊿POQ与⊿AOB相似。
