等腰三角形水平测试卷
图片预览



文档简介
等腰三角形同步测试题
时间:90分钟 分值:120分
一、选择题(每题3分,共30分)
1.等腰三角形的对称轴是( )
A.顶角的平分线 B.底边上的高
C.底边上的中线 D.底边上的高所在的直线
2.三角形内有一点,它到三角形三边的距离都相等,同时与三角形三顶点的距离也都相等,则这个三角形一定是( )
A.等腰三角形 B.等腰直角三角形 C.非等腰三角形 D.等边三角形
3.下列说法中,正确的有 ( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
4.等腰三角形(不等边)的角平分线、中线和高的条数总和是( )
A.3 B.5 C.7 D.9
5. 如图,把一张对边平行的纸条如图折叠,重合部分是 ( )
A. 等边三角形 B.等腰三角形
C. 直角三角形 D.无法确定
6.等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )
A.40° B.50° C.60° D.30°
7.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
8.已知三角形的三边长分别是;若的值为偶数,则的值有( )
A.个 B.个 C.个 D.个
9.等腰三角形的一个外角是80°,则其底角是( )
A.100° B.100°或40° C.40° D.80
10.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是( )
A.17cm B.22cm C.17cm或22cm D.18cm
二、填空题(每题3分,共30分)
11.已知:如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,不添辅助线,请你写出三个正确结论(1)______________;(2)______________;(3)______________.
12.如图(3),在△ABC中,∠ABC=70°,∠ACB=50°,D、C、B、E在一条直线上,且DB=AB,CE=AC,则∠E= ,∠D= ,∠DAE= .
13.如图,在ΔABC中,AC=DC=DB,∠ACD=100°,则∠B=__________。
14.三角形三内角的度数之比为1∶2∶3,最大边的长是8cm,则最小边的长是_______cm.
15.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
16.等腰三角形一底角为,底边上的高为9cm,则等腰三角形的腰长是_____cm,顶角是_________。
17.△ABC中,AB=AC,∠A+∠B=115°,则∠A= ,∠B= .
18.如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是_________.
19. △ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B=_______.
20. 等腰三角形一腰上的中线把周长分为6和9两个部分,则该等腰三角形腰长为 .
三、解答题
21.(8分)如图,△ABC 中,BE⊥AC于E,CF⊥AB于F,H是BE、CF的交点,且CF=BE.求证:AB=AC.
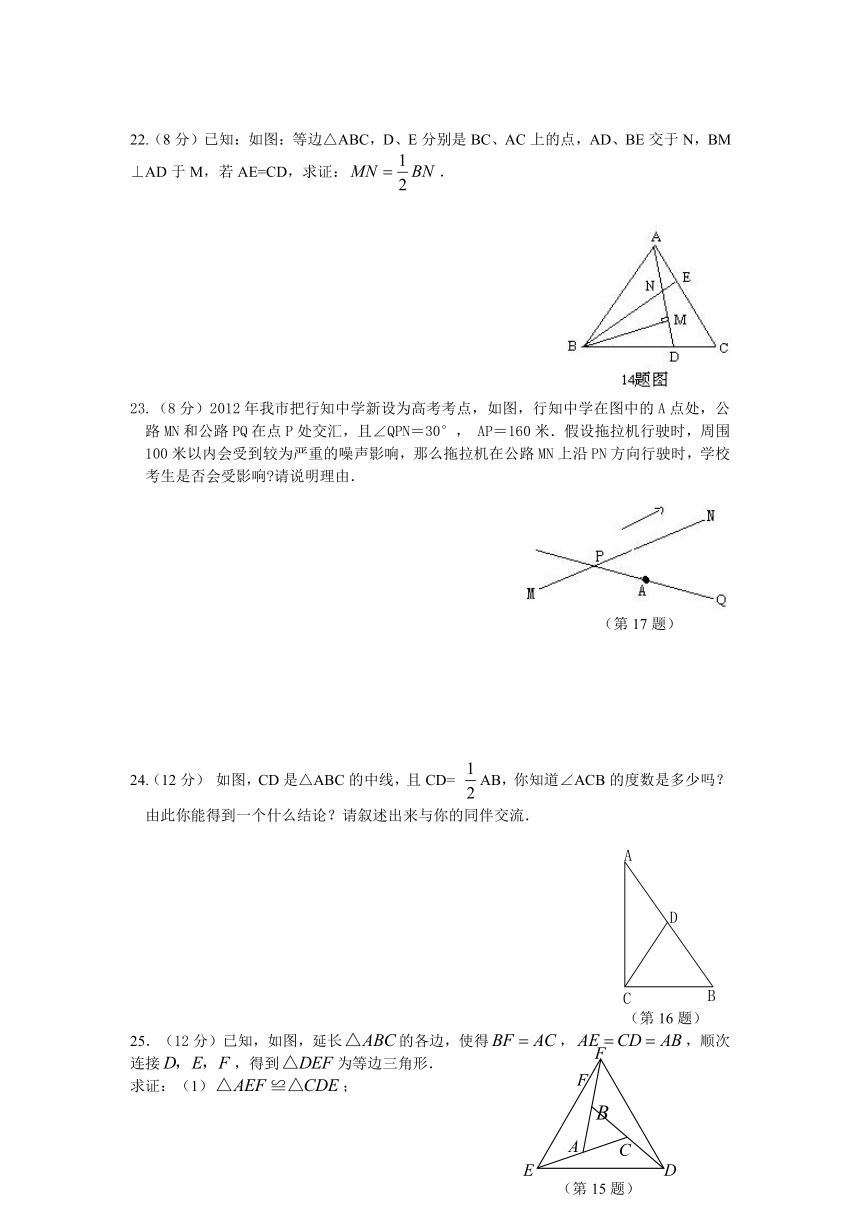
22.(8分)已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:.
23.(8分)2012年我市把行知中学新设为高考考点,如图,行知中学在图中的A点处,公路MN和公路PQ在点P处交汇,且∠QPN=30°, AP=160米.假设拖拉机行驶时,周围100米以内会受到较为严重的噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校考生是否会受影响 请说明理由.
24.(12分) 如图,CD是△ABC的中线,且CD= AB,你知道∠ACB的度数是多少吗?由此你能得到一个什么结论?请叙述出来与你的同伴交流.
25.(12分)已知,如图,延长的各边,使得,,顺次连接,得到为等边三角形.
求证:(1);
(2)为等边三角形.
26.(12分)(1)如图①所示,AD为的平分线,E为AD上一点,EF∥AC交AB于F,求证:为等腰三角形。
(2)如图②,中,的平分线与的平分线交于点D,过点D作BC的平行线交AB于点E,交AC于点F。
求证:EF=BD+CF
参考答案
一、选择题
1.D 2.D 3.D 4.C 5.B 6.A 7.D 8.D 9.C 10.B
二、填空题
11.(1)BD⊥AC; (2)∠ABD=∠CBD;(3)AB=BC=2CD;(4) ∠CBD=30°(或其它合理答案)
12.25° 35° 110°
13. 20°
14.4
15. 30海里
16.18cm 120°
17. 50°;65°
18. BD=CE(或∠BAD=∠CAE, ∠ADB=∠AEC, ∠BAE=∠CAD,BE=CD)
19. 20°或70°
20. 4或6
三.解答题
21. .证明:∵BE⊥AC,CF⊥AB
∴∠BEC=∠CFB=90°
在Rt△BCF和Rt△CBE中
BC=BC
CF=BE
∴Rt△BCF≌Rt△CBE(HL)
∴∠ABC=∠ACB
∴AB=AC
22.证明:∵等边△ABC,∴AC=BA,∠C=∠BAC=60°
在△ABE和△CAD中,∵BA=AC,∠BAC=∠C,AE=CD,∴△ABE≌△CAD(SAS)
∴∠2=∠1
∵∠BNM=∠3+∠2,∴∠BNM=∠3+∠1=∠BAC=60°
∵BM⊥AD,∴∠4+∠BNM=90°,∴∠4=30°
∵BM⊥AD,∴(直角三角形中,30°角所对直角边等于斜边的一半)
23. (1)如右图,过A点做MN的垂线,垂足为D,
∵在直角三角形PAD中,∠QPN=30°, AP=160米,
∴AD=
∴学校考生会受到影响.(考试期间要禁止拖拉机通行)
24.∠ACB=90°.结论:若一个三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形
25.证明:(1),,.
是等边三角形,.
又,.
(2)由,得,
,是等边三角形,
,,同理可得.
中,.
是等边三角形.
26. (1)证明: EF∥AC,∴∠AEF=∠CAE,∵AD为的平分线,∴∠EAF=∠CAE,∴∠EAF=∠AEF,∴AF=AE,即为等腰三角形。(2)EF∥BC,∴∠BDE=∠CBD,∵BD为的平分线,∴∠ABD=∠CBD,∴∠ABD=∠BDE,∴BE=DE,同理可得DF=FC,∴EF=ED+DF=BD+CF
备用:
(2009·黔东南)6、如图2,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A、30o B、40o C、45o D、36o
(2009·泰安)(本小题满分10分)
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD。
求证:BE=AD;
求证:AC是线段ED的垂直平分线;
△DBC是等腰三角形吗?并说明理由。
证明:(1)∵∠ABC=90°,BD⊥EC,
∴∠1与∠3互余,∠2与∠3互余,
∴∠1=∠2…………………………………………………1分
∵∠ABC=∠DAB=90°,AB=AC
∴△BAD≌△CBE…………………………………………2分
∴AD=BE……………………………………………………3分
(2)∵E是AB中点,
∴EB=EA
由(1)AD=BE得:AE=AD……………………………5分
∵AD∥BC
∴∠7=∠ACB=45°
∵∠6=45°
∴∠6=∠7
由等腰三角形的性质,得:EM=MD,AM⊥DE。
即,AC是线段ED的垂直平分线。……………………7分
(3)△DBC是等腰三角(CD=BD)……………………8分
理由如下:
由(2)得:CD=CE
由(1)得:CE=BD
∴CD=BD
∴△DBC是等腰三角形。…
2. 已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,用你学过的知识探索AC、CD、CE三条线段的长度有何关系 试写出探求过程.
证明:∵△ABC为正三角形,∴AB=AC,∠BAC=60°,
又∵△ADE为正三角形,∴AD=AE,∠DAE=60°,
∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∴
∴△ABD≌△ACE,
∴BD=CE,∵AC=BC, ∴BD=BC+CD=AC+CD, ∴CE=AC+CD
2.已知等腰三角形两腰上的高(或其延长线)相交所成的锐角是50°,求这个三角形的顶角的度数.
因高有在三角形内部和外部两种情况.
①高在三角形内部,如图3-1,两高相交所成的锐角∠BOE = 50°,由∠BOE+∠ABD = ∠A+∠ABD=90°得∠A = ∠BOE = 50°;
②高在三角形外部,如图3-2,等腰△ABC两腰上的高BE、CD的延长线相交与点O,由∠O+∠OBD = ∠EAB+∠ABE = 90°得∠EAB = ∠O = 50°,∠BAC = 130°.所以顶角度数为50°或130°.
3.(1)在等腰△ABC中,AB=AC,底边BC上任意一点P到两腰的距离之和等于一腰上的高,你能用面积法证明这个结论吗?
(2)若点P在直线BC上,上述结论是否成立?为什么?
(1)连接AP,由得:
∵AB=AC
∴CH=PE+PF
(2)同上.
4.如图,已知的中垂线交于点,交于点,有下面3个结论:
①射线是的角平分线;
②是等腰三角形;
③≌。
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明。
(1)正确的结论是①、②、③;(2)射线是的角平分线;证明:∵,∴,∵MN是AB的中垂线,∴AD=BD,∴,∴,∴射线是的角平分线.
5.有一个数学活动,其具体操作过程如下:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图(1));
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图(2)).
请解答在图(2)中,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论
△BMP是等边三角形.连结AN。∵EF垂直平分AB ∴AN = BN,由折叠知 AB = BN,∴AN = AB = BN ∴△ABN为等边三角形,∴∠ABN =60° ∴∠PBN =30°,又∵∠ABM =∠NBM =30°,∠BNM =∠A =90°,∴∠BPN =60°,∠MBP =∠MBN +∠PBN =60°∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°∴△BMP为等边三角形。
A
B
C
D
E
第10题图
A
B
C
F
E
13题图
H
(第17题)
(第16题)
(第15题)
时间:90分钟 分值:120分
一、选择题(每题3分,共30分)
1.等腰三角形的对称轴是( )
A.顶角的平分线 B.底边上的高
C.底边上的中线 D.底边上的高所在的直线
2.三角形内有一点,它到三角形三边的距离都相等,同时与三角形三顶点的距离也都相等,则这个三角形一定是( )
A.等腰三角形 B.等腰直角三角形 C.非等腰三角形 D.等边三角形
3.下列说法中,正确的有 ( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
4.等腰三角形(不等边)的角平分线、中线和高的条数总和是( )
A.3 B.5 C.7 D.9
5. 如图,把一张对边平行的纸条如图折叠,重合部分是 ( )
A. 等边三角形 B.等腰三角形
C. 直角三角形 D.无法确定
6.等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )
A.40° B.50° C.60° D.30°
7.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
8.已知三角形的三边长分别是;若的值为偶数,则的值有( )
A.个 B.个 C.个 D.个
9.等腰三角形的一个外角是80°,则其底角是( )
A.100° B.100°或40° C.40° D.80
10.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是( )
A.17cm B.22cm C.17cm或22cm D.18cm
二、填空题(每题3分,共30分)
11.已知:如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,不添辅助线,请你写出三个正确结论(1)______________;(2)______________;(3)______________.
12.如图(3),在△ABC中,∠ABC=70°,∠ACB=50°,D、C、B、E在一条直线上,且DB=AB,CE=AC,则∠E= ,∠D= ,∠DAE= .
13.如图,在ΔABC中,AC=DC=DB,∠ACD=100°,则∠B=__________。
14.三角形三内角的度数之比为1∶2∶3,最大边的长是8cm,则最小边的长是_______cm.
15.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
16.等腰三角形一底角为,底边上的高为9cm,则等腰三角形的腰长是_____cm,顶角是_________。
17.△ABC中,AB=AC,∠A+∠B=115°,则∠A= ,∠B= .
18.如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是_________.
19. △ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B=_______.
20. 等腰三角形一腰上的中线把周长分为6和9两个部分,则该等腰三角形腰长为 .
三、解答题
21.(8分)如图,△ABC 中,BE⊥AC于E,CF⊥AB于F,H是BE、CF的交点,且CF=BE.求证:AB=AC.
22.(8分)已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:.
23.(8分)2012年我市把行知中学新设为高考考点,如图,行知中学在图中的A点处,公路MN和公路PQ在点P处交汇,且∠QPN=30°, AP=160米.假设拖拉机行驶时,周围100米以内会受到较为严重的噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校考生是否会受影响 请说明理由.
24.(12分) 如图,CD是△ABC的中线,且CD= AB,你知道∠ACB的度数是多少吗?由此你能得到一个什么结论?请叙述出来与你的同伴交流.
25.(12分)已知,如图,延长的各边,使得,,顺次连接,得到为等边三角形.
求证:(1);
(2)为等边三角形.
26.(12分)(1)如图①所示,AD为的平分线,E为AD上一点,EF∥AC交AB于F,求证:为等腰三角形。
(2)如图②,中,的平分线与的平分线交于点D,过点D作BC的平行线交AB于点E,交AC于点F。
求证:EF=BD+CF
参考答案
一、选择题
1.D 2.D 3.D 4.C 5.B 6.A 7.D 8.D 9.C 10.B
二、填空题
11.(1)BD⊥AC; (2)∠ABD=∠CBD;(3)AB=BC=2CD;(4) ∠CBD=30°(或其它合理答案)
12.25° 35° 110°
13. 20°
14.4
15. 30海里
16.18cm 120°
17. 50°;65°
18. BD=CE(或∠BAD=∠CAE, ∠ADB=∠AEC, ∠BAE=∠CAD,BE=CD)
19. 20°或70°
20. 4或6
三.解答题
21. .证明:∵BE⊥AC,CF⊥AB
∴∠BEC=∠CFB=90°
在Rt△BCF和Rt△CBE中
BC=BC
CF=BE
∴Rt△BCF≌Rt△CBE(HL)
∴∠ABC=∠ACB
∴AB=AC
22.证明:∵等边△ABC,∴AC=BA,∠C=∠BAC=60°
在△ABE和△CAD中,∵BA=AC,∠BAC=∠C,AE=CD,∴△ABE≌△CAD(SAS)
∴∠2=∠1
∵∠BNM=∠3+∠2,∴∠BNM=∠3+∠1=∠BAC=60°
∵BM⊥AD,∴∠4+∠BNM=90°,∴∠4=30°
∵BM⊥AD,∴(直角三角形中,30°角所对直角边等于斜边的一半)
23. (1)如右图,过A点做MN的垂线,垂足为D,
∵在直角三角形PAD中,∠QPN=30°, AP=160米,
∴AD=
∴学校考生会受到影响.(考试期间要禁止拖拉机通行)
24.∠ACB=90°.结论:若一个三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形
25.证明:(1),,.
是等边三角形,.
又,.
(2)由,得,
,是等边三角形,
,,同理可得.
中,.
是等边三角形.
26. (1)证明: EF∥AC,∴∠AEF=∠CAE,∵AD为的平分线,∴∠EAF=∠CAE,∴∠EAF=∠AEF,∴AF=AE,即为等腰三角形。(2)EF∥BC,∴∠BDE=∠CBD,∵BD为的平分线,∴∠ABD=∠CBD,∴∠ABD=∠BDE,∴BE=DE,同理可得DF=FC,∴EF=ED+DF=BD+CF
备用:
(2009·黔东南)6、如图2,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A、30o B、40o C、45o D、36o
(2009·泰安)(本小题满分10分)
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD。
求证:BE=AD;
求证:AC是线段ED的垂直平分线;
△DBC是等腰三角形吗?并说明理由。
证明:(1)∵∠ABC=90°,BD⊥EC,
∴∠1与∠3互余,∠2与∠3互余,
∴∠1=∠2…………………………………………………1分
∵∠ABC=∠DAB=90°,AB=AC
∴△BAD≌△CBE…………………………………………2分
∴AD=BE……………………………………………………3分
(2)∵E是AB中点,
∴EB=EA
由(1)AD=BE得:AE=AD……………………………5分
∵AD∥BC
∴∠7=∠ACB=45°
∵∠6=45°
∴∠6=∠7
由等腰三角形的性质,得:EM=MD,AM⊥DE。
即,AC是线段ED的垂直平分线。……………………7分
(3)△DBC是等腰三角(CD=BD)……………………8分
理由如下:
由(2)得:CD=CE
由(1)得:CE=BD
∴CD=BD
∴△DBC是等腰三角形。…
2. 已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,用你学过的知识探索AC、CD、CE三条线段的长度有何关系 试写出探求过程.
证明:∵△ABC为正三角形,∴AB=AC,∠BAC=60°,
又∵△ADE为正三角形,∴AD=AE,∠DAE=60°,
∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∴
∴△ABD≌△ACE,
∴BD=CE,∵AC=BC, ∴BD=BC+CD=AC+CD, ∴CE=AC+CD
2.已知等腰三角形两腰上的高(或其延长线)相交所成的锐角是50°,求这个三角形的顶角的度数.
因高有在三角形内部和外部两种情况.
①高在三角形内部,如图3-1,两高相交所成的锐角∠BOE = 50°,由∠BOE+∠ABD = ∠A+∠ABD=90°得∠A = ∠BOE = 50°;
②高在三角形外部,如图3-2,等腰△ABC两腰上的高BE、CD的延长线相交与点O,由∠O+∠OBD = ∠EAB+∠ABE = 90°得∠EAB = ∠O = 50°,∠BAC = 130°.所以顶角度数为50°或130°.
3.(1)在等腰△ABC中,AB=AC,底边BC上任意一点P到两腰的距离之和等于一腰上的高,你能用面积法证明这个结论吗?
(2)若点P在直线BC上,上述结论是否成立?为什么?
(1)连接AP,由得:
∵AB=AC
∴CH=PE+PF
(2)同上.
4.如图,已知的中垂线交于点,交于点,有下面3个结论:
①射线是的角平分线;
②是等腰三角形;
③≌。
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明。
(1)正确的结论是①、②、③;(2)射线是的角平分线;证明:∵,∴,∵MN是AB的中垂线,∴AD=BD,∴,∴,∴射线是的角平分线.
5.有一个数学活动,其具体操作过程如下:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图(1));
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图(2)).
请解答在图(2)中,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论
△BMP是等边三角形.连结AN。∵EF垂直平分AB ∴AN = BN,由折叠知 AB = BN,∴AN = AB = BN ∴△ABN为等边三角形,∴∠ABN =60° ∴∠PBN =30°,又∵∠ABM =∠NBM =30°,∠BNM =∠A =90°,∴∠BPN =60°,∠MBP =∠MBN +∠PBN =60°∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°∴△BMP为等边三角形。
A
B
C
D
E
第10题图
A
B
C
F
E
13题图
H
(第17题)
(第16题)
(第15题)
