鲁教版五四制数学七年级上册第一章《三角形》单元综合练习—提高能力测试(word版含答案)
文档属性
| 名称 | 鲁教版五四制数学七年级上册第一章《三角形》单元综合练习—提高能力测试(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 563.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 00:00:00 | ||
图片预览


文档简介
第一章
三角形
【提高能力测试】
题型发散
1.选择题,把正确答案的代号填入题中括号内.
(1)下列各条件中,不能作出惟一直角三角形的是(
)
(A)已知两直角边
(B)已知两锐角
(C)已知一直角边和一锐角
(D)已知斜边和一直角边
(2)已知AM、AH、AD分别是△ABC的BC边上的中线、高线和∠A的平分线,AB≠AC,那么AM、AH、AD的位置关系为(
)
(A)AD在AM和AH之间
(B)AM在AD和AH之间
(C)AH在AD和AM之间
(D)不能确定
(3)已知三角形的两边长为2和7,第三边的数值是奇数,那么这个三角形的周长是(
)
(A)14
(B)15
(C)16
(D)17
(4)在△ABC中,若∠A=∠B=∠C,那么这个三角形是(
)
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)以上都不对
(5)已知线段m,n(m>n),用直尺和圆规作等腰△ABC,使AB=AC=m,BC=n,再分别以AB、AC为边向三角形外作等边△ABD和等边△ACE,连结BE、CD,那么(
)
(A)BE>CD
(U)BE=CD
(C)BE(D)BE≤CD
(6)在△ABC中,AB>AC,AD为BC边上的中线,则∠DAB与∠DAC的大小关系是(
)
(A)∠DAB>∠DAC
(B)∠DAB<∠DAC
(C)∠DAB=∠DAC
(D)不能确定
2.填空题.
(1)在△ABC中,AB=AC,BD平分∠ABC交AC于D,DE垂直平分AB,垂足为E,则∠C=______________
(2)在锐角△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC=___
_度.
(3)已知△ABC,D在AC上,∠A=,∠DBC=,∠C=,那么∠BDC=_________度,∠ABD=_________度,其中等腰三角形有__________
(4)边长为2,x-4,5的三根木条首尾相接组成三角形,则x的取值范围是______________.
(5)在△ABC中,如果,b=4n,则c=_______时,∠C=.
(6)在Rt△ABC中,AB=2AC,CD、CE分别是斜边上的中线和高,则∠DCE=____________.
解法发散
1.如图5—75,已知在△ABC中,AB=AC,延长AB到D,使
BD=AB,E为AB的中点,求证:CD=2CE.
(按原图与如下四个图(见图5-76(a)~(d))所作辅助线用五种方法证明)
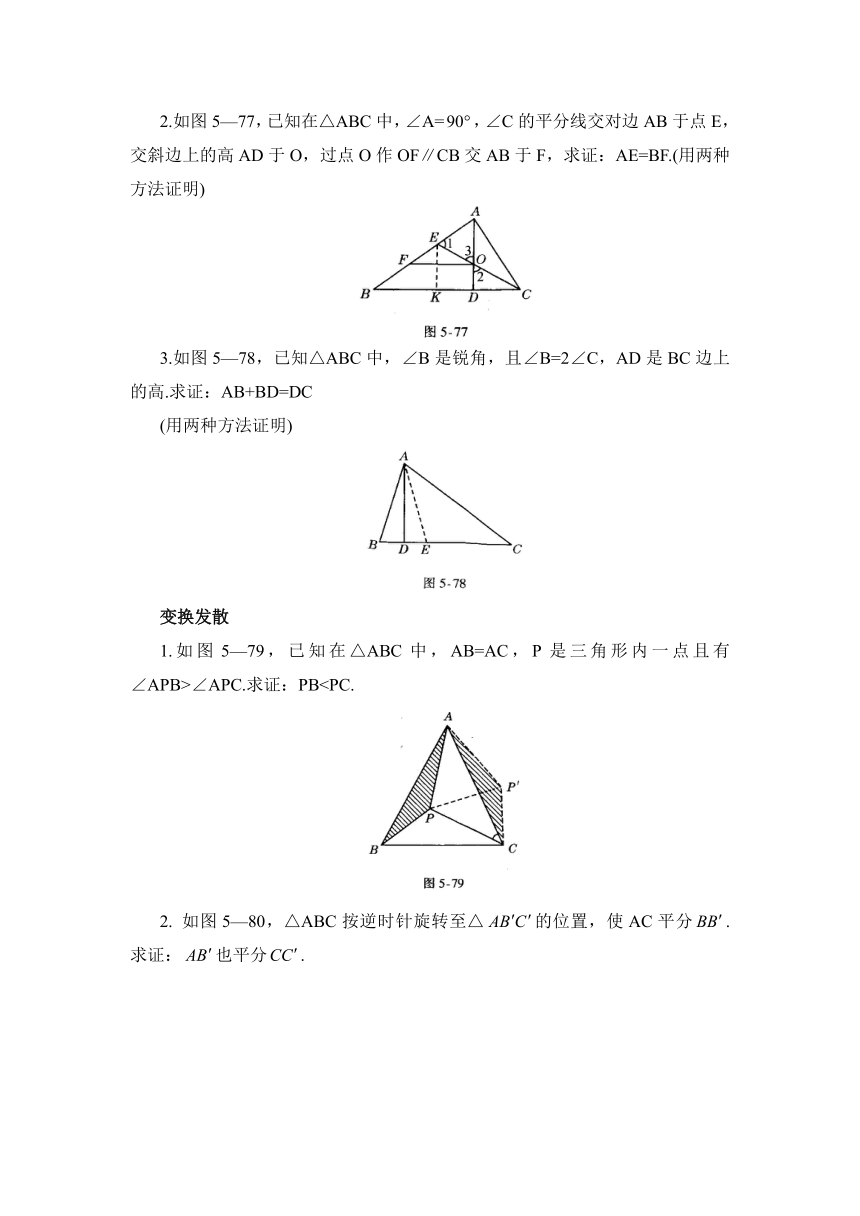
2.如图5—77,已知在△ABC中,∠A=,∠C的平分线交对边AB于点E,交斜边上的高AD于O,过点O作OF∥CB交AB于F,求证:AE=BF.(用两种方法证明)
3.如图5—78,已知△ABC中,∠B是锐角,且∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC
(用两种方法证明)
变换发散
1.如图5—79,已知在△ABC中,AB=AC,P是三角形内一点且有∠APB>∠APC.求证:PB2.
如图5—80,△ABC按逆时针旋转至△的位置,使AC平分.求证:也平分.
逆向发散
发散题
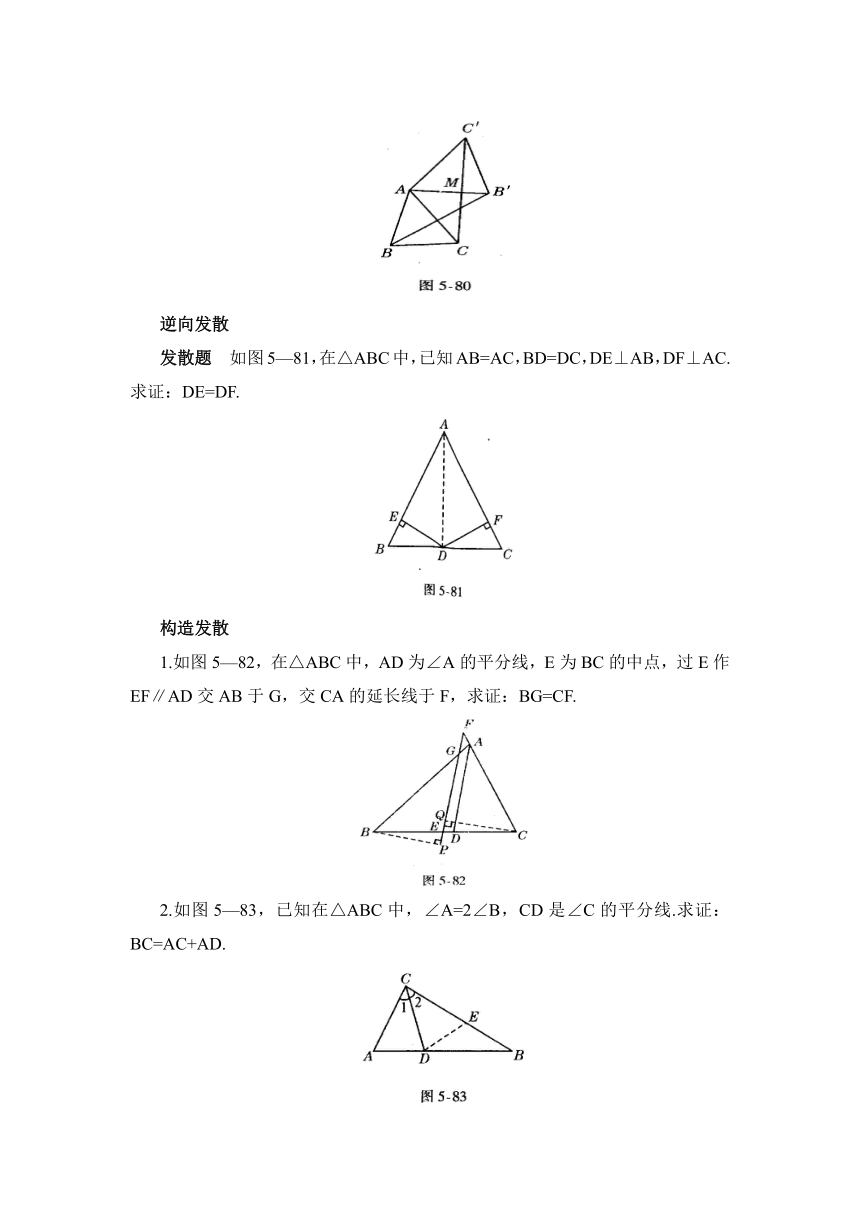
如图5—81,在△ABC中,已知AB=AC,BD=DC,DE⊥AB,DF⊥AC.求证:DE=DF.
构造发散
1.如图5—82,在△ABC中,AD为∠A的平分线,E为BC的中点,过E作EF∥AD交AB于G,交CA的延长线于F,求证:BG=CF.
2.如图5—83,已知在△ABC中,∠A=2∠B,CD是∠C的平分线.求证:BC=AC+AD.
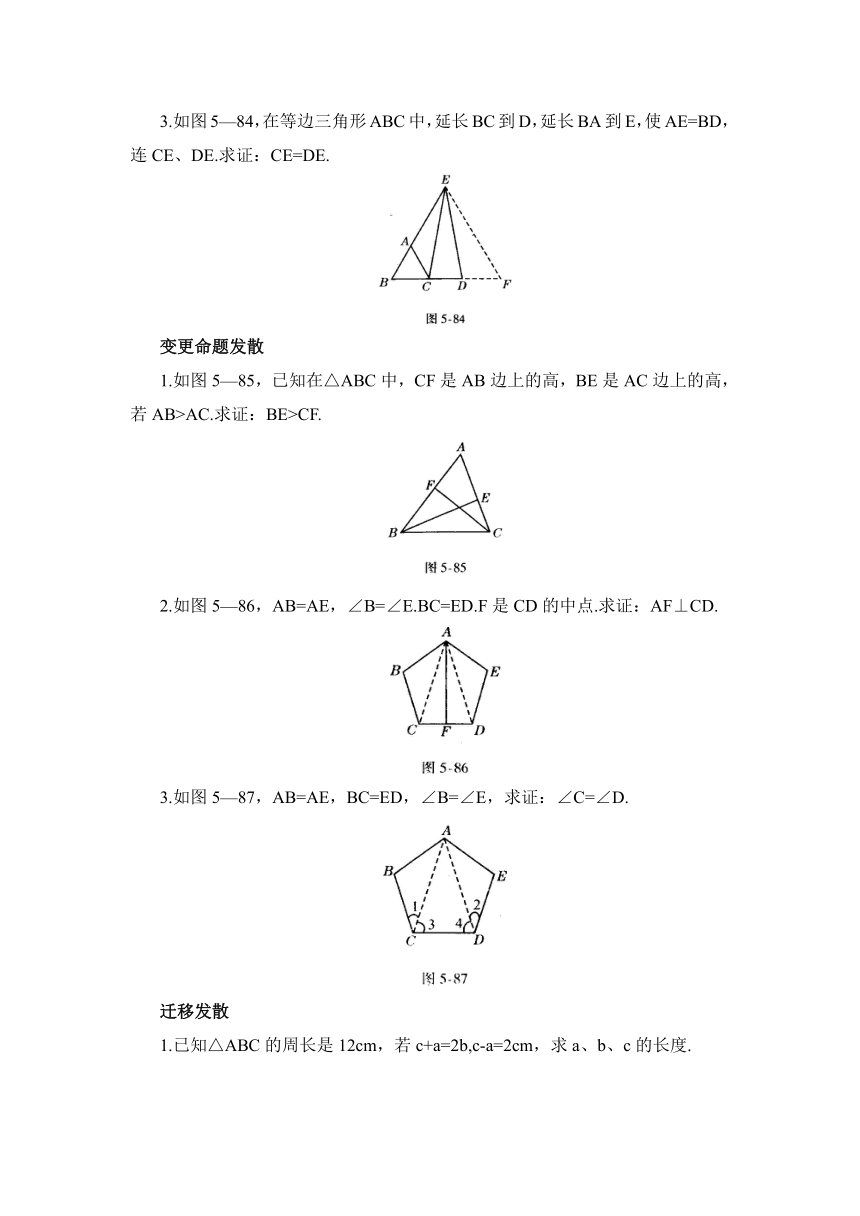
3.如图5—84,在等边三角形ABC中,延长BC到D,延长BA到E,使AE=BD,连CE、DE.求证:CE=DE.
变更命题发散
1.如图5—85,已知在△ABC中,CF是AB边上的高,BE是AC边上的高,若AB>AC.求证:BE>CF.
2.如图5—86,AB=AE,∠B=∠E.BC=ED.F是CD的中点.求证:AF⊥CD.
3.如图5—87,AB=AE,BC=ED,∠B=∠E,求证:∠C=∠D.
迁移发散
1.已知△ABC的周长是12cm,若c+a=2b,c-a=2cm,求a、b、c的长度.
2.如图5—88,已知△ABC中,AB=2CA,且CA为最小边.求证:(AB+BC+CA)综合发散
1.如图5—89,已知自Rt△ABC的直角顶点A作BC上的高AD.求证:AD+BC>AB+AC
2.如图5—90,C是线段AB上一点,分别以AC、CB为一边作等边三角形ACD和CBE,AE交CD于M,BD交CE于N.求证:
(1)△CMN是等边三角形;
(2)MN∥AB.
3.已知D是△ABC中∠BAC平分线AE上一点,AB>AC.求证:AB-AC>BD-DC.
4.在△ABC中,∠C=,AC=BC,过C在△ABC外作直线MN,使AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN;
(2)若过C在△ABC内作直线MN,当MN位于何位置时,AM、BN和MN之间满足关系式AM-BN=MN.并证明之.
5.如图5—91,已知:O是△ABC内一点.求证:(1)∠BOC>∠A;
(2)(BC+CA+AB)6.如图5—92,在等腰直角三角形ABC中,P为斜边BC的中点,D为BC上任一点,DE⊥AB,DF⊥AC.求证:PE=PF,PE⊥PF.
参考答案
【提高能力测试】
题型发散
1.(1)(B)
(2)(A)
(3)(C)
(4)(B)
(5)(B)
(6)(B)
2.(1)
(2)
(3),△ABC,△ABD,△BCD.
(4)7解法发散
1.证法1如图5—75,取CD的中点F,连结BF.
∵AB=BD,∴BF∥AC,且BF=AC.
∴∠2=∠ACB.∵AB=AC,
∴∠1=∠ACB.∴∠1=∠2
∵BE=AB,∴BE=BF.又∵BC=BC,
∴△BCE≌△BCF.∴CE=CF.∴CD=2CE.
以下四种证法省略.
2.证法1如图5—77,过点E作EK⊥BC,垂足为K.
∵E是∠C平分线,∠BAC=,
∴EK=EA.又∠1和∠2同是∠ACB的余角,
∴∠1=∠2,∠2=∠3,∠1=∠3.
∴AE=AO=EK,又FO∥BC,
∴∠AFO=∠EBK,∠AOF=∠EKB=,
∴Rt△AOF≌△EKB.
∴AF=EB.故AE=BF.
证法2如图过点O作OG∥AB交BC于G,则BGOF是平行四边形.
∴BF=GO.
∵∠AOE=∠1+∠3,∠AEO=∠B+∠2,
又∠BAC=,AD⊥BC,
∴∠B=∠1.∵CE是∠ACB的平分线,
∴∠2=∠3.∴∠AOE=∠AEO.
∴AE=AO.
在△AOC和△GOC中,
∵∠CGO=∠B=∠1,∠2=∠3,OC为公共边,
∴△AOC≌△GOC,AO=GO=AE=BF,故AE=BF.
3.证法1在DC上截取DE=DB,连结AE.
∵AD⊥DE,BD=DE.AB=AE.∴∠B=∠AEB.
∵∠B=2∠C.∴∠AEB=2∠C.
∴∠C=∠EAC.∴AE=EC=AB.
∵DC=DE+EC,∴AB+BD=DC.
证法2如图,延长CB到F,使BF=AB,连AF.
在△AFB中,
∵AB=BF.∴∠F=∠BAF.
∵∠ABC=∠F+∠BAF,即∠ABC=2∠F,
又∠ABC=2∠C,∠F=∠C.
∴AC=AF.又AD⊥FC,FD=DC.
∵FD=FB+BD,FD=AB+BD,即AB+BD=DC.
变换发散
1.分析:∵AB=AC,本题以等腰三角形ABC的顶点A为旋转中心,顶角(∠BAC)为旋转角,旋转到,的位置.
欲证,连,只须证.
∵,又
∴.∴.
问题得证.
证明:以A为顶点,以AC为边,在△ABC外作,在上取,连.
∵AB=AC.∴.
∴,连
∵,∴
∴.∴
∵.∴PC>PB.
2.证法1在△中,
∵,AC平分,∴AC是等腰的顶角平分线,
即,.
又在△AMC和中,
∵,,AM=AM,
∴.
∴.故平分.
证法2可通过证明,
从而得,可证得,平分.
逆向发散
提示连结AD,AD是等腰三角形的顶角平分线,本题应用角平分线的两个互逆定理证明.
构造发散
1.分析:因有∠BGE=∠F,欲证BG=CF可考虑证明其所在的三角形全等,而△GBE和△CFE明显不全等,故须构造含已知角和欲证线段为边的直角三角形,或使夹已知角的另一对边相等,又注意到条件中有BE=CE,若作BP⊥EF,CQ⊥EF,须证BP=CQ,然此易由Rt△BPE≌Rt△CQE得到.
证明:过B、C分别作BP⊥EF,CO⊥FE.
垂足分别为P、Q,则BP∥CQ阅.
∴∠PBE=∠QCE,而BE=CE,
∴Rt△QPE≌Rt△CAE.BP=CQ.
又EF∥DA,AD平分∠A,∠BGE=∠F.
∴Rt△BPG≌Rt△CQF.故BC=CF.
2.证明:在CB上截取CE=CA,连DE,构造新三角形△CDE.
在△ACD和△ECD中,
∵AC=EC,∠1=∠2,CD=CD,
∴△ACD≌△ECD.∴AD=DE,∠CED=∠A.
∵∠A=2∠B,∴∠CED=2∠B.
∴∠B=∠EDB.∴DE=EB=AD.
∵BC=CE+EB,∴BC=AC+AD.
3.分析:延长BD到F,使DF=BC连结EF,则BE=BF,构造△DEF,欲证△BCE≌△FDE.
证明:∵∠B=,BE=BF,∴△EFB是等边三角形.
∴∠B=∠F.∵BC=DF,BE=FE,
∴△BCE≌△FDE.∴CE=DE.
变更命题发散
1.∵,
∴.
∵AB>AC,∴BE>CF.
2.连结AC、AD.在△ABC和△AED中,
∵AB=AE,∠B=∠E,BC=ED,∴△ABC≌△AED.
∴AC=AD.在△ACF和△ADF中,
∵AC=AD,AF=AF,CF=DF,∴△ACF≌△ADF.
∴∠AFC=∠AFD.∵∠CFD=,
∴∠AFC=.∴AF⊥CD.
3.连结AC、AD.
∵AB=AE,∠B=∠E,BC=ED,∴△ABC≌△AED(SAS).
∴∠1=∠2,AC=AD(全等三角形的对应角、对应边相等).
∴在△ACD中,∠3=∠4.
∴∠1+∠3=∠2+∠4,即∠BCD=∠EDC.
迁移发散
1.解:依题意,得方程组:
解方程组,得:a=3(cm),b=4(cm),c=5(cm).
2.设AC=a,AB=2a,周长AB+BC+CA=l,则:
AB+BC+CA=2a+a+BC.
∵BC>a,∴AB+BC+CA>2a+a+a=4a.∴
又BC则l=AB+BC+CA<2a+3a+a=6a.
∴.综上.
∴即(AB+BC+CA)综合发散
1.分析:在BC上截取BE=AB,作EF⊥AC于F,连结AE,构造Rt△AEF和Rt△ADE,证明这两个直角三角形全等.
证明:如图,在BC上截取BE=AB,作EF⊥AC于F,连结AE.
∵BA⊥AC,EF⊥AC,
∴AB∥EF.∴∠BAE=∠2.
又∠BAE=∠1,∴∠1=∠2.
在Rt△ADE和Rt△AEF中,
∵AE=AE,∠1=∠2,
∴Rt△ADE≌Rt△AEF.
∴AD=AF.
∵BE=AB,EC>FC,
∴AD+BE+FC>AF+AB+FC,
即AD+BC>AB+AC.
2.(1)∵△ACD和△CBE是等边三角形,
∴AC=CD,CE=CB.
∵∠ACD=∠ECB=,∴∠BCE=.
∴∠ACE=∠DCB.
∴△ACE≌△DCB.(SAS).∴∠AEC=∠DBC.
在△MCE和△NCB中,
∵∠AEC=∠DBC,CE=CB,∠MCE=∠NCB=,
∴△MCE≌△NCB.
∴MC=NC.
又∠MCN=,∴△CMN是等边三角形.
(2)∵∠NMC=∠ACM=,∴MN∥AB.
3.∵AB>AC,在AB上截取AF=AC,连结DF,则△ADF≌△ADC,
∴DF=DC.
在△DBF中,BF>DB-DF,
∴BF>DB-DC.
∵BF=AB-AC.即有AB-AC>DB-DC.
4.(1)如图,
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠BNC=.
∵∠ACB=.
∴∠MCA+∠NCB=.
∴∠ACM=∠CBN.又AC=CB,
∴△ACM≌△CBN,MC=BN,AM=CN.
∴MN=AM+BN.
(2)若过C在△ABC内作直线MN,当MN经过等腰直角△ABC的底边AB的中点时,MN、AM、BN之间满足关系式MN=AM-BN.
证明略.
5.(1)如图延长BO交AC于点D.
∵∠BOC是△OCD的外角,
∴∠BOC>∠1.
同理可证∠1>∠A,
∴∠BOC>∠A.
(2)连结OA.在△ABO中,
∵AB同理BC∴BC+CA+AB<2(OA+OB+OC)
即(BC+CA+AB)6.连结AP.
∵AP=BP=PC,AF=ED=BE,∠PAF=∠PBE=,
∴△PAF≌△PBE.
∴∠APF=∠BPE.∴PE=PF.
∠APF+∠APE=∠BPE+∠APE.
又∠APF+∠APE+∠BPE+∠APE=,
∴∠EPA+∠APF=.即PE⊥PF.
三角形
【提高能力测试】
题型发散
1.选择题,把正确答案的代号填入题中括号内.
(1)下列各条件中,不能作出惟一直角三角形的是(
)
(A)已知两直角边
(B)已知两锐角
(C)已知一直角边和一锐角
(D)已知斜边和一直角边
(2)已知AM、AH、AD分别是△ABC的BC边上的中线、高线和∠A的平分线,AB≠AC,那么AM、AH、AD的位置关系为(
)
(A)AD在AM和AH之间
(B)AM在AD和AH之间
(C)AH在AD和AM之间
(D)不能确定
(3)已知三角形的两边长为2和7,第三边的数值是奇数,那么这个三角形的周长是(
)
(A)14
(B)15
(C)16
(D)17
(4)在△ABC中,若∠A=∠B=∠C,那么这个三角形是(
)
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)以上都不对
(5)已知线段m,n(m>n),用直尺和圆规作等腰△ABC,使AB=AC=m,BC=n,再分别以AB、AC为边向三角形外作等边△ABD和等边△ACE,连结BE、CD,那么(
)
(A)BE>CD
(U)BE=CD
(C)BE
(6)在△ABC中,AB>AC,AD为BC边上的中线,则∠DAB与∠DAC的大小关系是(
)
(A)∠DAB>∠DAC
(B)∠DAB<∠DAC
(C)∠DAB=∠DAC
(D)不能确定
2.填空题.
(1)在△ABC中,AB=AC,BD平分∠ABC交AC于D,DE垂直平分AB,垂足为E,则∠C=______________
(2)在锐角△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC=___
_度.
(3)已知△ABC,D在AC上,∠A=,∠DBC=,∠C=,那么∠BDC=_________度,∠ABD=_________度,其中等腰三角形有__________
(4)边长为2,x-4,5的三根木条首尾相接组成三角形,则x的取值范围是______________.
(5)在△ABC中,如果,b=4n,则c=_______时,∠C=.
(6)在Rt△ABC中,AB=2AC,CD、CE分别是斜边上的中线和高,则∠DCE=____________.
解法发散
1.如图5—75,已知在△ABC中,AB=AC,延长AB到D,使
BD=AB,E为AB的中点,求证:CD=2CE.
(按原图与如下四个图(见图5-76(a)~(d))所作辅助线用五种方法证明)
2.如图5—77,已知在△ABC中,∠A=,∠C的平分线交对边AB于点E,交斜边上的高AD于O,过点O作OF∥CB交AB于F,求证:AE=BF.(用两种方法证明)
3.如图5—78,已知△ABC中,∠B是锐角,且∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC
(用两种方法证明)
变换发散
1.如图5—79,已知在△ABC中,AB=AC,P是三角形内一点且有∠APB>∠APC.求证:PB
如图5—80,△ABC按逆时针旋转至△的位置,使AC平分.求证:也平分.
逆向发散
发散题
如图5—81,在△ABC中,已知AB=AC,BD=DC,DE⊥AB,DF⊥AC.求证:DE=DF.
构造发散
1.如图5—82,在△ABC中,AD为∠A的平分线,E为BC的中点,过E作EF∥AD交AB于G,交CA的延长线于F,求证:BG=CF.
2.如图5—83,已知在△ABC中,∠A=2∠B,CD是∠C的平分线.求证:BC=AC+AD.
3.如图5—84,在等边三角形ABC中,延长BC到D,延长BA到E,使AE=BD,连CE、DE.求证:CE=DE.
变更命题发散
1.如图5—85,已知在△ABC中,CF是AB边上的高,BE是AC边上的高,若AB>AC.求证:BE>CF.
2.如图5—86,AB=AE,∠B=∠E.BC=ED.F是CD的中点.求证:AF⊥CD.
3.如图5—87,AB=AE,BC=ED,∠B=∠E,求证:∠C=∠D.
迁移发散
1.已知△ABC的周长是12cm,若c+a=2b,c-a=2cm,求a、b、c的长度.
2.如图5—88,已知△ABC中,AB=2CA,且CA为最小边.求证:(AB+BC+CA)
1.如图5—89,已知自Rt△ABC的直角顶点A作BC上的高AD.求证:AD+BC>AB+AC
2.如图5—90,C是线段AB上一点,分别以AC、CB为一边作等边三角形ACD和CBE,AE交CD于M,BD交CE于N.求证:
(1)△CMN是等边三角形;
(2)MN∥AB.
3.已知D是△ABC中∠BAC平分线AE上一点,AB>AC.求证:AB-AC>BD-DC.
4.在△ABC中,∠C=,AC=BC,过C在△ABC外作直线MN,使AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN;
(2)若过C在△ABC内作直线MN,当MN位于何位置时,AM、BN和MN之间满足关系式AM-BN=MN.并证明之.
5.如图5—91,已知:O是△ABC内一点.求证:(1)∠BOC>∠A;
(2)(BC+CA+AB)
参考答案
【提高能力测试】
题型发散
1.(1)(B)
(2)(A)
(3)(C)
(4)(B)
(5)(B)
(6)(B)
2.(1)
(2)
(3),△ABC,△ABD,△BCD.
(4)7
1.证法1如图5—75,取CD的中点F,连结BF.
∵AB=BD,∴BF∥AC,且BF=AC.
∴∠2=∠ACB.∵AB=AC,
∴∠1=∠ACB.∴∠1=∠2
∵BE=AB,∴BE=BF.又∵BC=BC,
∴△BCE≌△BCF.∴CE=CF.∴CD=2CE.
以下四种证法省略.
2.证法1如图5—77,过点E作EK⊥BC,垂足为K.
∵E是∠C平分线,∠BAC=,
∴EK=EA.又∠1和∠2同是∠ACB的余角,
∴∠1=∠2,∠2=∠3,∠1=∠3.
∴AE=AO=EK,又FO∥BC,
∴∠AFO=∠EBK,∠AOF=∠EKB=,
∴Rt△AOF≌△EKB.
∴AF=EB.故AE=BF.
证法2如图过点O作OG∥AB交BC于G,则BGOF是平行四边形.
∴BF=GO.
∵∠AOE=∠1+∠3,∠AEO=∠B+∠2,
又∠BAC=,AD⊥BC,
∴∠B=∠1.∵CE是∠ACB的平分线,
∴∠2=∠3.∴∠AOE=∠AEO.
∴AE=AO.
在△AOC和△GOC中,
∵∠CGO=∠B=∠1,∠2=∠3,OC为公共边,
∴△AOC≌△GOC,AO=GO=AE=BF,故AE=BF.
3.证法1在DC上截取DE=DB,连结AE.
∵AD⊥DE,BD=DE.AB=AE.∴∠B=∠AEB.
∵∠B=2∠C.∴∠AEB=2∠C.
∴∠C=∠EAC.∴AE=EC=AB.
∵DC=DE+EC,∴AB+BD=DC.
证法2如图,延长CB到F,使BF=AB,连AF.
在△AFB中,
∵AB=BF.∴∠F=∠BAF.
∵∠ABC=∠F+∠BAF,即∠ABC=2∠F,
又∠ABC=2∠C,∠F=∠C.
∴AC=AF.又AD⊥FC,FD=DC.
∵FD=FB+BD,FD=AB+BD,即AB+BD=DC.
变换发散
1.分析:∵AB=AC,本题以等腰三角形ABC的顶点A为旋转中心,顶角(∠BAC)为旋转角,旋转到,的位置.
欲证,连,只须证.
∵,又
∴.∴.
问题得证.
证明:以A为顶点,以AC为边,在△ABC外作,在上取,连.
∵AB=AC.∴.
∴,连
∵,∴
∴.∴
∵.∴PC>PB.
2.证法1在△中,
∵,AC平分,∴AC是等腰的顶角平分线,
即,.
又在△AMC和中,
∵,,AM=AM,
∴.
∴.故平分.
证法2可通过证明,
从而得,可证得,平分.
逆向发散
提示连结AD,AD是等腰三角形的顶角平分线,本题应用角平分线的两个互逆定理证明.
构造发散
1.分析:因有∠BGE=∠F,欲证BG=CF可考虑证明其所在的三角形全等,而△GBE和△CFE明显不全等,故须构造含已知角和欲证线段为边的直角三角形,或使夹已知角的另一对边相等,又注意到条件中有BE=CE,若作BP⊥EF,CQ⊥EF,须证BP=CQ,然此易由Rt△BPE≌Rt△CQE得到.
证明:过B、C分别作BP⊥EF,CO⊥FE.
垂足分别为P、Q,则BP∥CQ阅.
∴∠PBE=∠QCE,而BE=CE,
∴Rt△QPE≌Rt△CAE.BP=CQ.
又EF∥DA,AD平分∠A,∠BGE=∠F.
∴Rt△BPG≌Rt△CQF.故BC=CF.
2.证明:在CB上截取CE=CA,连DE,构造新三角形△CDE.
在△ACD和△ECD中,
∵AC=EC,∠1=∠2,CD=CD,
∴△ACD≌△ECD.∴AD=DE,∠CED=∠A.
∵∠A=2∠B,∴∠CED=2∠B.
∴∠B=∠EDB.∴DE=EB=AD.
∵BC=CE+EB,∴BC=AC+AD.
3.分析:延长BD到F,使DF=BC连结EF,则BE=BF,构造△DEF,欲证△BCE≌△FDE.
证明:∵∠B=,BE=BF,∴△EFB是等边三角形.
∴∠B=∠F.∵BC=DF,BE=FE,
∴△BCE≌△FDE.∴CE=DE.
变更命题发散
1.∵,
∴.
∵AB>AC,∴BE>CF.
2.连结AC、AD.在△ABC和△AED中,
∵AB=AE,∠B=∠E,BC=ED,∴△ABC≌△AED.
∴AC=AD.在△ACF和△ADF中,
∵AC=AD,AF=AF,CF=DF,∴△ACF≌△ADF.
∴∠AFC=∠AFD.∵∠CFD=,
∴∠AFC=.∴AF⊥CD.
3.连结AC、AD.
∵AB=AE,∠B=∠E,BC=ED,∴△ABC≌△AED(SAS).
∴∠1=∠2,AC=AD(全等三角形的对应角、对应边相等).
∴在△ACD中,∠3=∠4.
∴∠1+∠3=∠2+∠4,即∠BCD=∠EDC.
迁移发散
1.解:依题意,得方程组:
解方程组,得:a=3(cm),b=4(cm),c=5(cm).
2.设AC=a,AB=2a,周长AB+BC+CA=l,则:
AB+BC+CA=2a+a+BC.
∵BC>a,∴AB+BC+CA>2a+a+a=4a.∴
又BC
∴.综上.
∴即(AB+BC+CA)
1.分析:在BC上截取BE=AB,作EF⊥AC于F,连结AE,构造Rt△AEF和Rt△ADE,证明这两个直角三角形全等.
证明:如图,在BC上截取BE=AB,作EF⊥AC于F,连结AE.
∵BA⊥AC,EF⊥AC,
∴AB∥EF.∴∠BAE=∠2.
又∠BAE=∠1,∴∠1=∠2.
在Rt△ADE和Rt△AEF中,
∵AE=AE,∠1=∠2,
∴Rt△ADE≌Rt△AEF.
∴AD=AF.
∵BE=AB,EC>FC,
∴AD+BE+FC>AF+AB+FC,
即AD+BC>AB+AC.
2.(1)∵△ACD和△CBE是等边三角形,
∴AC=CD,CE=CB.
∵∠ACD=∠ECB=,∴∠BCE=.
∴∠ACE=∠DCB.
∴△ACE≌△DCB.(SAS).∴∠AEC=∠DBC.
在△MCE和△NCB中,
∵∠AEC=∠DBC,CE=CB,∠MCE=∠NCB=,
∴△MCE≌△NCB.
∴MC=NC.
又∠MCN=,∴△CMN是等边三角形.
(2)∵∠NMC=∠ACM=,∴MN∥AB.
3.∵AB>AC,在AB上截取AF=AC,连结DF,则△ADF≌△ADC,
∴DF=DC.
在△DBF中,BF>DB-DF,
∴BF>DB-DC.
∵BF=AB-AC.即有AB-AC>DB-DC.
4.(1)如图,
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠BNC=.
∵∠ACB=.
∴∠MCA+∠NCB=.
∴∠ACM=∠CBN.又AC=CB,
∴△ACM≌△CBN,MC=BN,AM=CN.
∴MN=AM+BN.
(2)若过C在△ABC内作直线MN,当MN经过等腰直角△ABC的底边AB的中点时,MN、AM、BN之间满足关系式MN=AM-BN.
证明略.
5.(1)如图延长BO交AC于点D.
∵∠BOC是△OCD的外角,
∴∠BOC>∠1.
同理可证∠1>∠A,
∴∠BOC>∠A.
(2)连结OA.在△ABO中,
∵AB
即(BC+CA+AB)
∵AP=BP=PC,AF=ED=BE,∠PAF=∠PBE=,
∴△PAF≌△PBE.
∴∠APF=∠BPE.∴PE=PF.
∠APF+∠APE=∠BPE+∠APE.
又∠APF+∠APE+∠BPE+∠APE=,
∴∠EPA+∠APF=.即PE⊥PF.
