2021—2022学年人教版数学八年级上册13.1.1 轴对称 课件(26张)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册13.1.1 轴对称 课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 22:37:14 | ||
图片预览








文档简介
(共26张PPT)
第十三章
轴对称
13.1
轴对称
13.1.1
轴对称
教学目标
1.通过展示轴对称图形的图片,初步认识轴对称图形.
2.能够识别简单的轴对称图形及其对称轴.
3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称现象共同特征.
课前导入
1.做一做:把一张纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?它有什么特征?
观察
8
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线即折痕所在的直线就是它的对称轴.
嗨!对称轴在这儿呢!
9
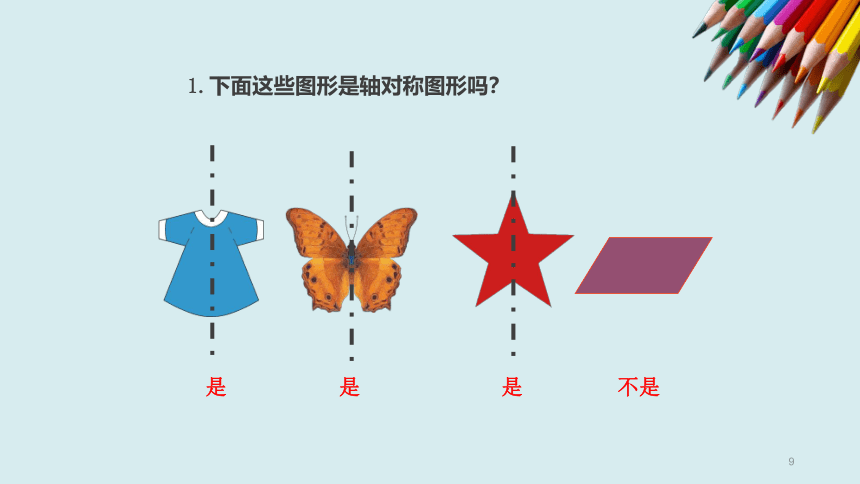
是
是
是
不是
1.下面这些图形是轴对称图形吗?
10
2.下面这些图形是轴对称图形吗?如果是,有几条对称轴?
11
12
1、有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
2、对称轴通常画成虚线,是直线,不能画成线段.
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
对称轴
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
例1.下列四组图片中有哪几组图形成轴对称?
B
D
C
A
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
轴对称的性质
思考:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质
知识要点
例2
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )A.130°
B.150°
C.40°
D.65°
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
A
20
全等
全等
对称
1.成轴对称的两个图形全等吗?(
)
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?(
)这两个图形对称吗?(
)
课堂练习
21
3.把一圆形纸片两次对折后,得到右图,然后沿虚线剪开,得到两部分,其中一部分展开后的平面图形是(
)
A
B
C
D
B
22
4.下面四个中文艺术字中,不是轴对称图形的是(
)
【解析】选C.只有“千”字不是轴对称图形,上面的撇不对称.
5.找出下面每个轴对称图形的对称轴.
6.找出下文中成轴对称的文字:
一;
三;
个;
八;
十;
来;
苦;
天;
中.
一叶孤舟,坐着两三个骚客,启用四桨五帆,经过六滩七湾,历尽八颠九簸,可叹十分来迟.十年寒窗,进了九八家书院,抛却七情六欲,苦读五经四书,考了三番两次,今天一定要中.
7.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
8.如图,Rt△ABC中,∠ACB=
90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
10°
课堂小结
通过本课时的学习,需要我们:
1.了解轴对称图形和两个图形关于某直线对称的概念.
3.了解轴对称图形与两个图形关于某直线对称的区别
和联系.
2.能识别简单的轴对称图形及其对称轴(直线),
能找出两个图形关于某直线对称的对称点.
第十三章
轴对称
13.1
轴对称
13.1.1
轴对称
教学目标
1.通过展示轴对称图形的图片,初步认识轴对称图形.
2.能够识别简单的轴对称图形及其对称轴.
3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称现象共同特征.
课前导入
1.做一做:把一张纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?它有什么特征?
观察
8
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线即折痕所在的直线就是它的对称轴.
嗨!对称轴在这儿呢!
9
是
是
是
不是
1.下面这些图形是轴对称图形吗?
10
2.下面这些图形是轴对称图形吗?如果是,有几条对称轴?
11
12
1、有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
2、对称轴通常画成虚线,是直线,不能画成线段.
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
对称轴
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
例1.下列四组图片中有哪几组图形成轴对称?
B
D
C
A
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
轴对称的性质
思考:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质
知识要点
例2
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )A.130°
B.150°
C.40°
D.65°
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
A
20
全等
全等
对称
1.成轴对称的两个图形全等吗?(
)
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?(
)这两个图形对称吗?(
)
课堂练习
21
3.把一圆形纸片两次对折后,得到右图,然后沿虚线剪开,得到两部分,其中一部分展开后的平面图形是(
)
A
B
C
D
B
22
4.下面四个中文艺术字中,不是轴对称图形的是(
)
【解析】选C.只有“千”字不是轴对称图形,上面的撇不对称.
5.找出下面每个轴对称图形的对称轴.
6.找出下文中成轴对称的文字:
一;
三;
个;
八;
十;
来;
苦;
天;
中.
一叶孤舟,坐着两三个骚客,启用四桨五帆,经过六滩七湾,历尽八颠九簸,可叹十分来迟.十年寒窗,进了九八家书院,抛却七情六欲,苦读五经四书,考了三番两次,今天一定要中.
7.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
8.如图,Rt△ABC中,∠ACB=
90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
10°
课堂小结
通过本课时的学习,需要我们:
1.了解轴对称图形和两个图形关于某直线对称的概念.
3.了解轴对称图形与两个图形关于某直线对称的区别
和联系.
2.能识别简单的轴对称图形及其对称轴(直线),
能找出两个图形关于某直线对称的对称点.
