2021-2022学年人教版数学八年级上册 12.2全等三角形的判定(四) H L课件(15张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 12.2全等三角形的判定(四) H L课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 117.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 22:40:26 | ||
图片预览

文档简介
(共15张PPT)
12.2全等三角形的判定(四)
H
L
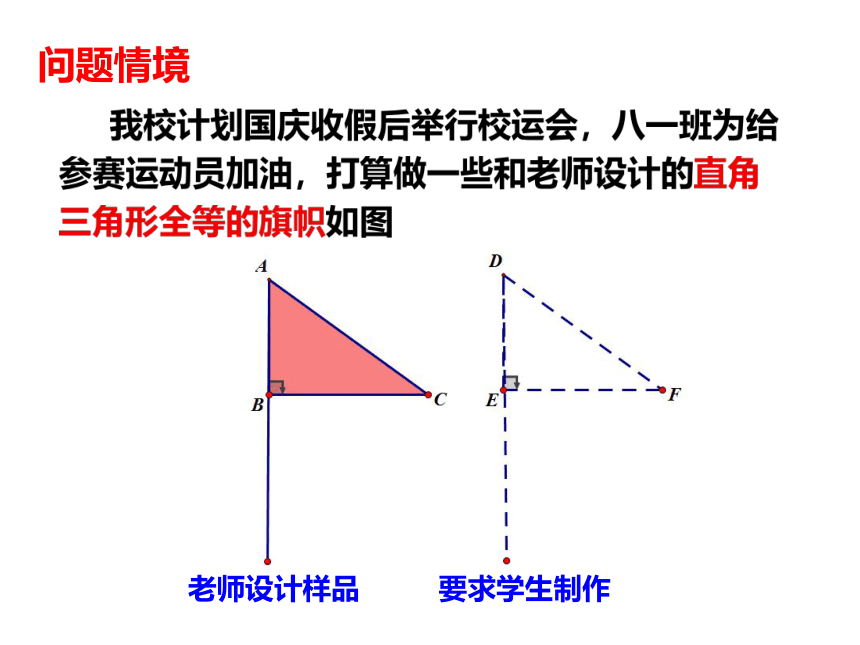
我校计划国庆收假后举行校运会,八一班为给参赛运动员加油,打算做一些和老师设计的直角三角形全等的旗帜如图
问题情境
老师设计样品
要求学生制作
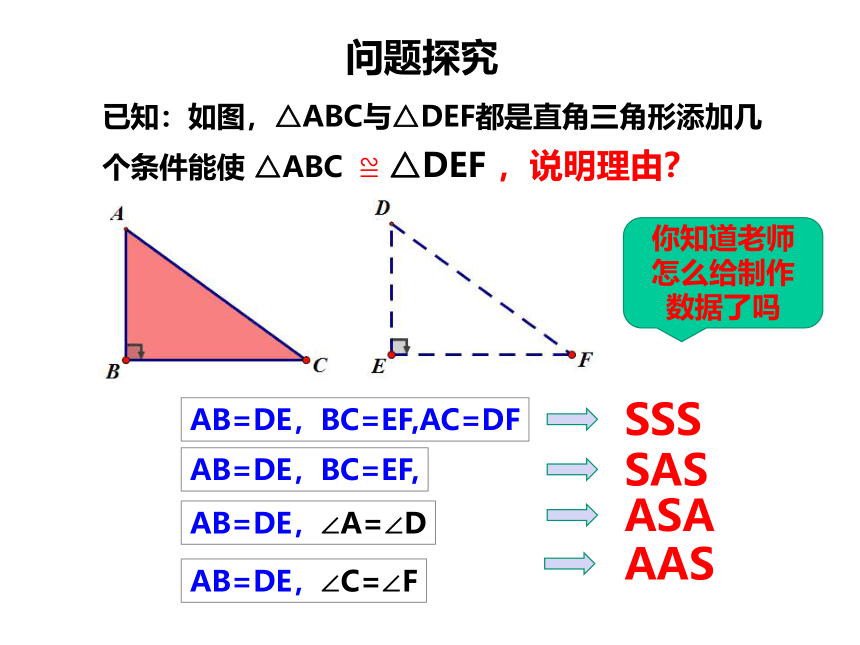
问题探究
已知:如图,△ABC与△DEF都是直角三角形添加几个条件能使
△ABC
≌
△DEF
,说明理由?
AB=DE,BC=EF,AC=DF
SSS
AB=DE,BC=EF,
AB=DE,∠A=∠D
AB=DE,∠C=∠F
SAS
ASA
AAS
你知道老师怎么给制作数据了吗
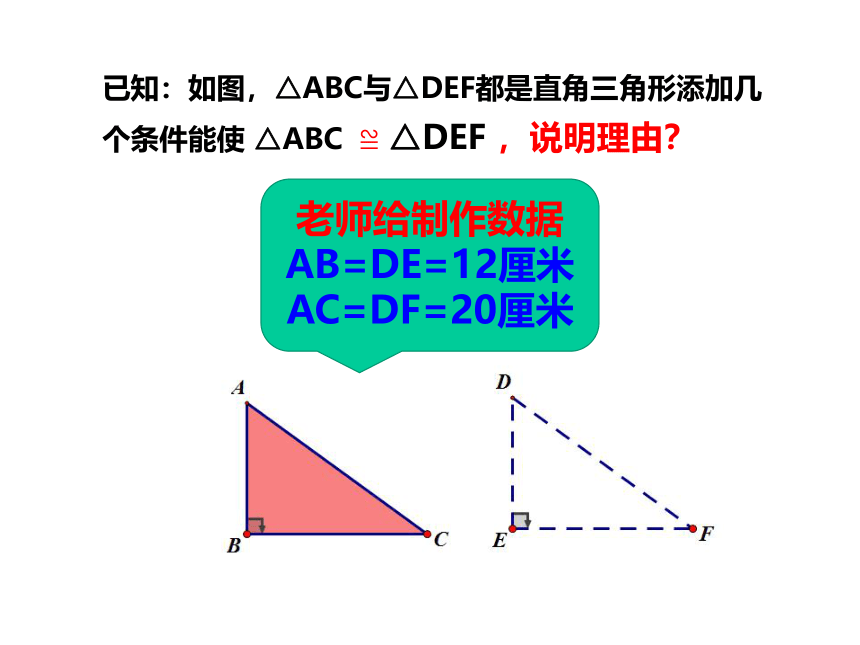
已知:如图,△ABC与△DEF都是直角三角形添加几个条件能使
△ABC
≌
△DEF
,说明理由?
老师给制作数据
AB=DE=12厘米AC=DF=20厘米
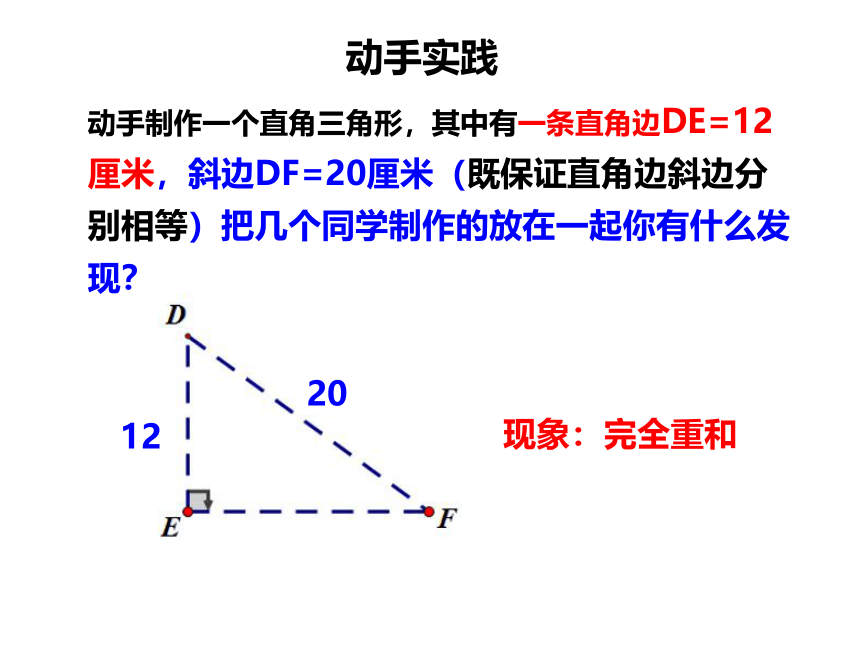
动手实践
动手制作一个直角三角形,其中有一条直角边DE=12厘米,斜边DF=20厘米(既保证直角边斜边分别相等)把几个同学制作的放在一起你有什么发现?
12
20
现象:完全重和
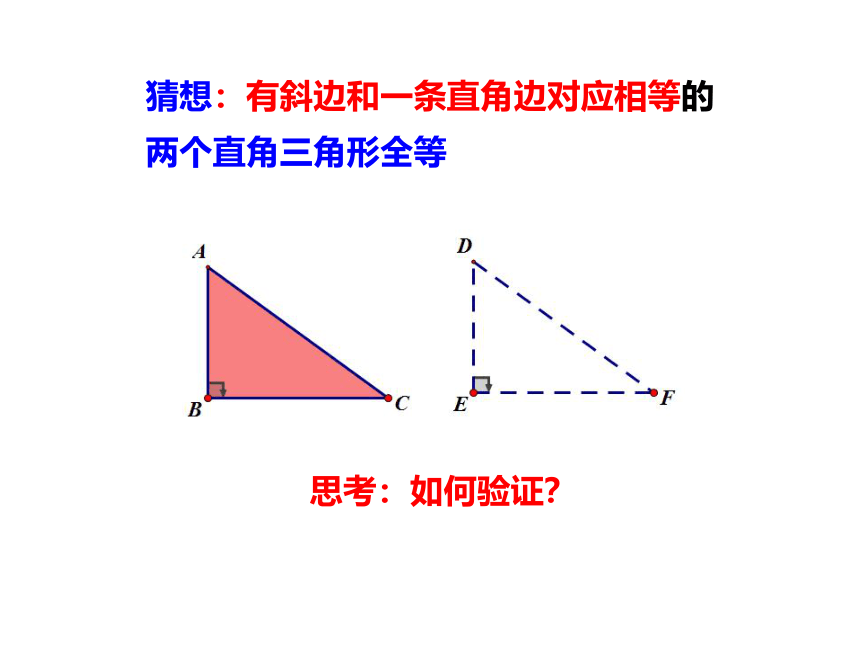
猜想:有斜边和一条直角边对应相等的
两个直角三角形全等
思考:如何验证?
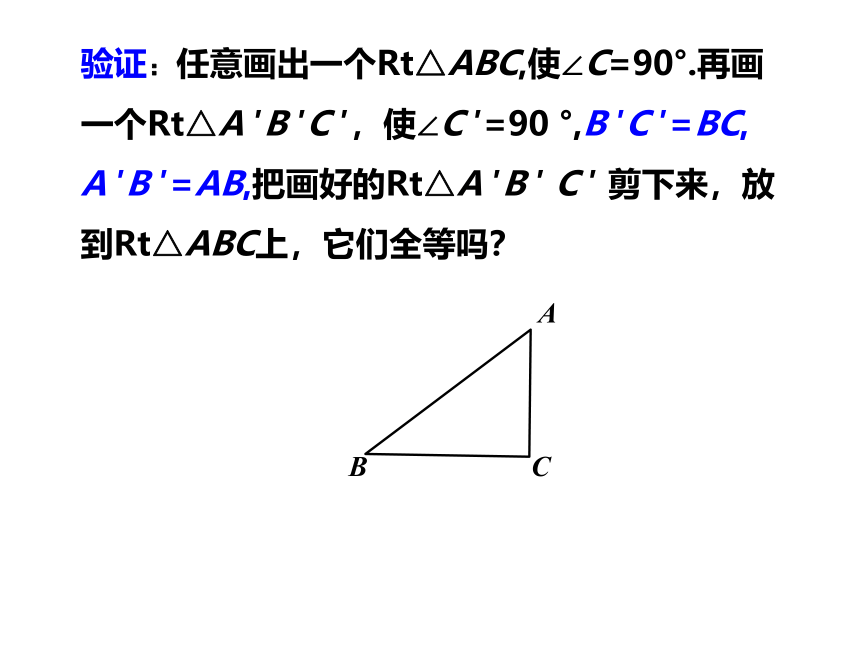
验证:任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A
′B
′C
′,使∠C
′=90
°,B
′C
′=BC,
A
′B
′=AB,把画好的Rt△A
′B
′
C
′
剪下来,放到Rt△ABC上,它们全等吗?
A
B
C
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'
为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
想一想:从中你能发现什么规律?
C
′
N
M
A
B
C
A
′
B
′
HL
“斜边、直角边”判定方法
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
A′B′C′
中,
∴Rt△ABC
≌
Rt△
A′B′C′
(HL).
∵∠C=∠C′=90°,
AB=A′B′,
BC=B′C′,
(1)
_______,∠A=∠D
(
ASA
)
(2)
AC=DF,________
(SAS)
(3)
AB=DE,BC=EF
(
)
(4)
AC=DF,
______
(
HL
)
(5)
∠A=∠D,
BC=EF
(
)
(6)
________,AC=DF
(
AAS
)
例1
把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
∠B=∠E
A
B
C
D
F
E
例2:如图,在△ABC和△DEF中,AP、DQ分别是高,并AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
思维拓展
变式一
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
BC=EF
变式二
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
AC=DF
A
F
C
E
D
B
如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
课后训练.
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“
ASA
”
“
AAS
”
“
SSS
”
“
SAS
”
“
ASA
”
“
AAS
”
“
HL
”
灵活运用各种方法证明直角三角形全等
“
SSS
”
课后小结
12.2全等三角形的判定(四)
H
L
我校计划国庆收假后举行校运会,八一班为给参赛运动员加油,打算做一些和老师设计的直角三角形全等的旗帜如图
问题情境
老师设计样品
要求学生制作
问题探究
已知:如图,△ABC与△DEF都是直角三角形添加几个条件能使
△ABC
≌
△DEF
,说明理由?
AB=DE,BC=EF,AC=DF
SSS
AB=DE,BC=EF,
AB=DE,∠A=∠D
AB=DE,∠C=∠F
SAS
ASA
AAS
你知道老师怎么给制作数据了吗
已知:如图,△ABC与△DEF都是直角三角形添加几个条件能使
△ABC
≌
△DEF
,说明理由?
老师给制作数据
AB=DE=12厘米AC=DF=20厘米
动手实践
动手制作一个直角三角形,其中有一条直角边DE=12厘米,斜边DF=20厘米(既保证直角边斜边分别相等)把几个同学制作的放在一起你有什么发现?
12
20
现象:完全重和
猜想:有斜边和一条直角边对应相等的
两个直角三角形全等
思考:如何验证?
验证:任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A
′B
′C
′,使∠C
′=90
°,B
′C
′=BC,
A
′B
′=AB,把画好的Rt△A
′B
′
C
′
剪下来,放到Rt△ABC上,它们全等吗?
A
B
C
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'
为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
想一想:从中你能发现什么规律?
C
′
N
M
A
B
C
A
′
B
′
HL
“斜边、直角边”判定方法
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
A′B′C′
中,
∴Rt△ABC
≌
Rt△
A′B′C′
(HL).
∵∠C=∠C′=90°,
AB=A′B′,
BC=B′C′,
(1)
_______,∠A=∠D
(
ASA
)
(2)
AC=DF,________
(SAS)
(3)
AB=DE,BC=EF
(
)
(4)
AC=DF,
______
(
HL
)
(5)
∠A=∠D,
BC=EF
(
)
(6)
________,AC=DF
(
AAS
)
例1
把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
∠B=∠E
A
B
C
D
F
E
例2:如图,在△ABC和△DEF中,AP、DQ分别是高,并AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
思维拓展
变式一
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
BC=EF
变式二
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
AC=DF
A
F
C
E
D
B
如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
课后训练.
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“
ASA
”
“
AAS
”
“
SSS
”
“
SAS
”
“
ASA
”
“
AAS
”
“
HL
”
灵活运用各种方法证明直角三角形全等
“
SSS
”
课后小结
