甘肃省兰州市第二十七中学2020-2021学年高二下学期期末考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 甘肃省兰州市第二十七中学2020-2021学年高二下学期期末考试数学(文)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 10:23:28 | ||
图片预览



文档简介
兰州二十七中2020——2021学年度第二学期期末试卷
高二数学(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.
满分150分,
考试时间为120分钟.
第Ⅰ卷(选择题
共60分)
一、选择题(下列各题只有一个选项符合要求,请将正确选项的代码填入答题卡中,每小题5分,共60分)
1.设集合A={x|1<x<4},集合B={x|x2-2x-3≤0},则A∩(?RB)=( )
A.(1,4)
B.(3,4)
C.(1,3)
D.(1,2)∪(3,4)
(
)
3.函数的最小正周期和最大值分别是(
)
A.和
B.和2
C.和
D.和2
4.若满足约束条件则的最小值为(
)
A.18
B.10
C.6
D.4
5.当时,在同一坐标系中,函数的图象是
(
)
.
A
B
C
D
6.生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取3只,则恰有2只测量过该指标的概率为
A.
B.
C.
D.
7.下列函数中最小值为4的是(
)
A.
B.
C.
D.
8.设f(x)为奇函数,且当x≥0时,f(x)=,则当x<0时,f(x)=(
)
A.
B.
C.
D.
9.在右图的正方体中,分别为棱和棱的中点,
则异面直线和所成的角为(
)
A.
B.
C.
D.
10.若圆C的半径为1,圆心在第一象限,且与直线和轴都相切,则该圆的标准方程是
(
)
A.
B.
C.
D.
11.程序框图(如图)的运算结果为
A.24
B.12
C.36
D.26
12.已知函数f(x)=g(x)=x2-2x,
设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数
a的取值范围为(
).
A.[-1,3]
B.(1,
2)
C.(1,3)
D.[-1,2]
第Ⅱ卷(非选择题
共90分)
2、填空题
(本大题共4小题,每小题5分,共20分。请把正确答案填在答题卡的横线上)
13.已知函数f(x)=x2+x+a在区间(0,1)上有零点,则实数a的取值范围是________.
14.若数列{an}的通项公式为an=2n+2n-1,则数列{an}的前n项和为________.
15.记的内角A,B,C的对边分别为a,b,c,面积为,,,则________.
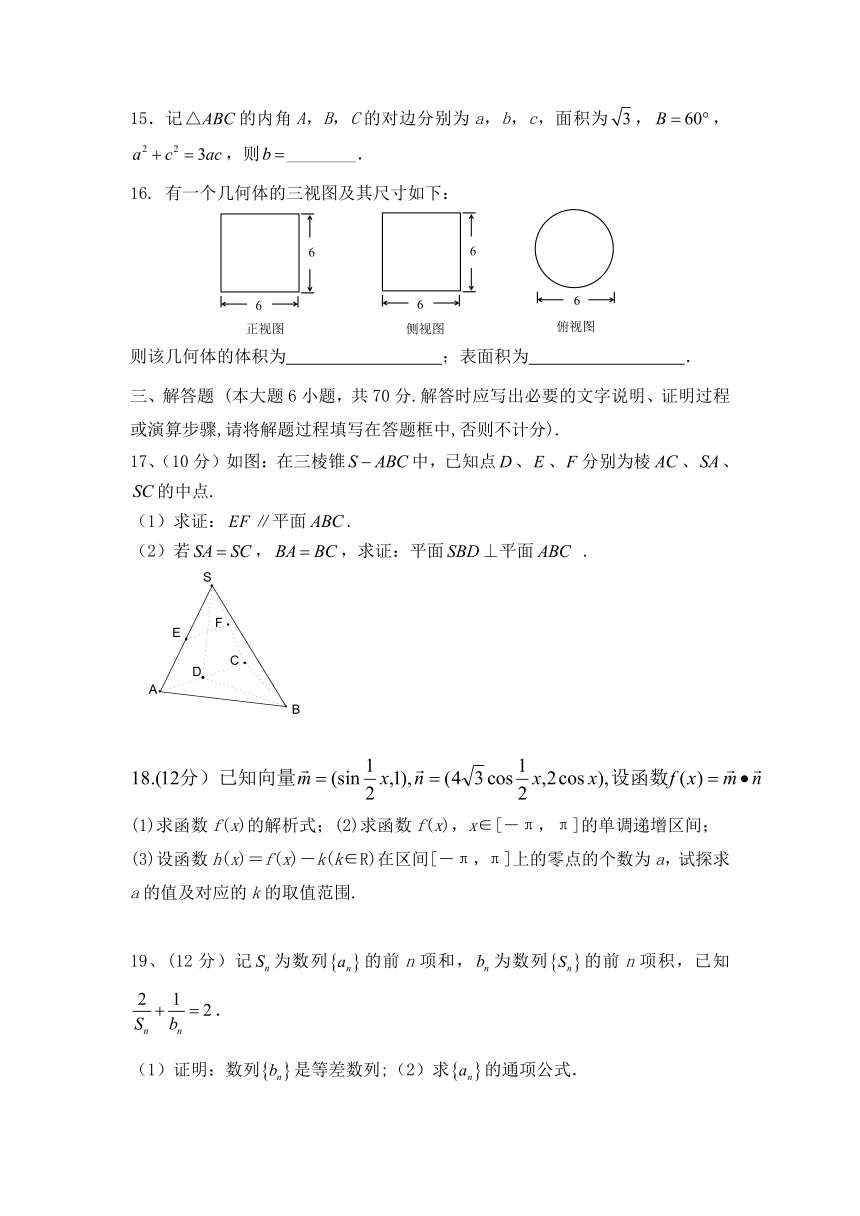
16.
有一个几何体的三视图及其尺寸如下:
则该几何体的体积为 ;表面积为 .
三、解答题
(本大题6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤,请将解题过程填写在答题框中,否则不计分).
17、(10分)如图:在三棱锥中,已知点、、分别为棱、、的中点.
(1)求证:∥平面.
(2)若,,求证:平面⊥平面
.
(1)求函数f(x)的解析式;(2)求函数f(x),x∈[-π,π]的单调递增区间;
(3)设函数h(x)=f(x)-k(k∈R)在区间[-π,π]上的零点的个数为a,试探求a的值及对应的k的取值范围.
19、(12分)记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;(2)求的通项公式.
20.某中学团委组织了一次知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率
21、(12分)已知圆.
(Ⅰ)此方程表示圆,求的取值范围;
(Ⅱ)若(1)中的圆与直线相交于、两点,且
(为坐标原点),求的值;
22.(12分)通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力(f(x)的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位:分),可以有以下公式:
f(x)=
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
兰州二十七中2020~2021第二学期期末考试参考答案
高二数学(文科)
一、选择题(12×5分=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
C
C
C
B
C
D
B
B
A
A
二、填空题(4×5分=20分)
13、(-2,0)
14、2n+1+n2-2
15、
16、54π
54π
三、解答题
17
证明:(1)∵是的中位线,
∴∥.
又∵平面,平面,
∴∥平面............5分
(2)∵,,∴.∵,,∴.
又∵平面,平面,,∴平面,
又∵平面,∴平面⊥平面5.。。。。。............5分
18.
.........................4分
(3)∵函数h(x)=f(x)-k(k∈R)在区间[-π,π]上的零点的个数为n,
即函数y=f(x)的图象和直线y=k在区间[-π,π]上的零点的个数为n,结合函数f(x)的图象可得:
当k>4,或
k<-4时,n=0;
当k=4,或
k=-4时,n=1;
当-4<k<-2,或-2<k<4时,n=2;
当k=-2时,n=3.................................................4分
19解:
20.解:(1)设分数在[70,80)内的频率为m,根据频率分布直方图
有(0.01
+
0.015×2
+
0.025
+
0.005)×10
+m?=
1,解得m=
0.3???
所以分数在[70,80)内的频率为0.3?
2分
???
4分
(2)10
(0.015+0.03+0.025+0.005)=0.75
所以及格率是75%。???????????????
.6分
45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.00?
9分
所以平均分是71.00??????
8分
21
解析:(1)方程,可化为(x-1)2+(y-2)2=5-m,
∵此方程表示圆,∴5-m>0,即m<5.
……………5分
(2)
消去x得(4-2y)2+y2-2×(4-2y)-4y+m=0,化简得5y2-16y+m+8=0.
设M(x1,y1),N(x2,y2),则
由OM⊥ON得y1y2+x1x2=0, 即y1y2+(4-2y1)(4-2y2)=0,
∴16-8(y1+y2)+5y1y2=0. 将①②两式代入上式得
16-8×+5×=0,解之得m=.
………12分
22、解析: (1)当0f(x)=-0.1x2+2.6x+43
=-0.1(x-13)2+59.9,
故f(x)在0当10当x>16时,f(x)为减函数,且f(x)<59.
因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.
(2)f(5)=-0.1(5-13)2+59.9=53.5,
f(20)=-320+107=47<53.5,
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
(3)当0解得x=6或x=20(舍),
当x>16时,令f(x)=55,
解得x=17.
因此学生达到(含超过)55的接受能力的时间为17-6=11<13,
所以老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.
x
y
1
1
o
o
y
x
1
1
x
y
o
1
1
o
y
x
1
1
6
6
6
6
6
正视图
侧视图
俯视图
高二数学(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.
满分150分,
考试时间为120分钟.
第Ⅰ卷(选择题
共60分)
一、选择题(下列各题只有一个选项符合要求,请将正确选项的代码填入答题卡中,每小题5分,共60分)
1.设集合A={x|1<x<4},集合B={x|x2-2x-3≤0},则A∩(?RB)=( )
A.(1,4)
B.(3,4)
C.(1,3)
D.(1,2)∪(3,4)
(
)
3.函数的最小正周期和最大值分别是(
)
A.和
B.和2
C.和
D.和2
4.若满足约束条件则的最小值为(
)
A.18
B.10
C.6
D.4
5.当时,在同一坐标系中,函数的图象是
(
)
.
A
B
C
D
6.生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取3只,则恰有2只测量过该指标的概率为
A.
B.
C.
D.
7.下列函数中最小值为4的是(
)
A.
B.
C.
D.
8.设f(x)为奇函数,且当x≥0时,f(x)=,则当x<0时,f(x)=(
)
A.
B.
C.
D.
9.在右图的正方体中,分别为棱和棱的中点,
则异面直线和所成的角为(
)
A.
B.
C.
D.
10.若圆C的半径为1,圆心在第一象限,且与直线和轴都相切,则该圆的标准方程是
(
)
A.
B.
C.
D.
11.程序框图(如图)的运算结果为
A.24
B.12
C.36
D.26
12.已知函数f(x)=g(x)=x2-2x,
设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数
a的取值范围为(
).
A.[-1,3]
B.(1,
2)
C.(1,3)
D.[-1,2]
第Ⅱ卷(非选择题
共90分)
2、填空题
(本大题共4小题,每小题5分,共20分。请把正确答案填在答题卡的横线上)
13.已知函数f(x)=x2+x+a在区间(0,1)上有零点,则实数a的取值范围是________.
14.若数列{an}的通项公式为an=2n+2n-1,则数列{an}的前n项和为________.
15.记的内角A,B,C的对边分别为a,b,c,面积为,,,则________.
16.
有一个几何体的三视图及其尺寸如下:
则该几何体的体积为 ;表面积为 .
三、解答题
(本大题6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤,请将解题过程填写在答题框中,否则不计分).
17、(10分)如图:在三棱锥中,已知点、、分别为棱、、的中点.
(1)求证:∥平面.
(2)若,,求证:平面⊥平面
.
(1)求函数f(x)的解析式;(2)求函数f(x),x∈[-π,π]的单调递增区间;
(3)设函数h(x)=f(x)-k(k∈R)在区间[-π,π]上的零点的个数为a,试探求a的值及对应的k的取值范围.
19、(12分)记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;(2)求的通项公式.
20.某中学团委组织了一次知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率
21、(12分)已知圆.
(Ⅰ)此方程表示圆,求的取值范围;
(Ⅱ)若(1)中的圆与直线相交于、两点,且
(为坐标原点),求的值;
22.(12分)通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力(f(x)的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位:分),可以有以下公式:
f(x)=
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
兰州二十七中2020~2021第二学期期末考试参考答案
高二数学(文科)
一、选择题(12×5分=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
C
C
C
B
C
D
B
B
A
A
二、填空题(4×5分=20分)
13、(-2,0)
14、2n+1+n2-2
15、
16、54π
54π
三、解答题
17
证明:(1)∵是的中位线,
∴∥.
又∵平面,平面,
∴∥平面............5分
(2)∵,,∴.∵,,∴.
又∵平面,平面,,∴平面,
又∵平面,∴平面⊥平面5.。。。。。............5分
18.
.........................4分
(3)∵函数h(x)=f(x)-k(k∈R)在区间[-π,π]上的零点的个数为n,
即函数y=f(x)的图象和直线y=k在区间[-π,π]上的零点的个数为n,结合函数f(x)的图象可得:
当k>4,或
k<-4时,n=0;
当k=4,或
k=-4时,n=1;
当-4<k<-2,或-2<k<4时,n=2;
当k=-2时,n=3.................................................4分
19解:
20.解:(1)设分数在[70,80)内的频率为m,根据频率分布直方图
有(0.01
+
0.015×2
+
0.025
+
0.005)×10
+m?=
1,解得m=
0.3???
所以分数在[70,80)内的频率为0.3?
2分
???
4分
(2)10
(0.015+0.03+0.025+0.005)=0.75
所以及格率是75%。???????????????
.6分
45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.00?
9分
所以平均分是71.00??????
8分
21
解析:(1)方程,可化为(x-1)2+(y-2)2=5-m,
∵此方程表示圆,∴5-m>0,即m<5.
……………5分
(2)
消去x得(4-2y)2+y2-2×(4-2y)-4y+m=0,化简得5y2-16y+m+8=0.
设M(x1,y1),N(x2,y2),则
由OM⊥ON得y1y2+x1x2=0, 即y1y2+(4-2y1)(4-2y2)=0,
∴16-8(y1+y2)+5y1y2=0. 将①②两式代入上式得
16-8×+5×=0,解之得m=.
………12分
22、解析: (1)当0
=-0.1(x-13)2+59.9,
故f(x)在0
因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.
(2)f(5)=-0.1(5-13)2+59.9=53.5,
f(20)=-320+107=47<53.5,
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
(3)当0
当x>16时,令f(x)=55,
解得x=17.
因此学生达到(含超过)55的接受能力的时间为17-6=11<13,
所以老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.
x
y
1
1
o
o
y
x
1
1
x
y
o
1
1
o
y
x
1
1
6
6
6
6
6
正视图
侧视图
俯视图
同课章节目录
