08浮力实验题 ---2021-2022学年上学期上海市沪教版九年级物理同步巩固复习作业(含答案解析)
文档属性
| 名称 | 08浮力实验题 ---2021-2022学年上学期上海市沪教版九年级物理同步巩固复习作业(含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 913.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(试用本) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-26 00:00:00 | ||
图片预览




文档简介
目录
TOC
\o
"1-1"
\h
\u
一.阿基米德原理的应用(共4小题)
1
二.浮力大小的计算(共2小题)
3
三.探究影响浮力大小因素的实验(共20小题)
4
四.物体的浮沉条件及其应用(共4小题)
24
参考答案
27
一.阿基米德原理的应用(共4小题)
27
二.浮力大小的计算(共2小题)
29
三.探究影响浮力大小因素的实验(共20小题)
30
四.物体的浮沉条件及其应用(共4小题)
43
一.阿基米德原理的应用(共4小题)
1.某小组同学想探究漂浮在液面上的实心物体露出液面的体积V露与什么因素有关。他们选用了若干不同的实心圆柱体漂浮在不同液体中进行实验,并将物体的密度ρ物,物体的体积V物、液体的密度ρ液,以及物体露出液面的体积V露记录在表中。
实验序号
ρ物(×103千克/米3)
V物(×10﹣6/米3)
ρ液(×103千克/米3)
V露(×10﹣6米3)
1
0.4
10
1.0
6
2
0.4
15
1.0
9
3
0.4
20
1.0
12
4
0.6
15
0.9
5
5
0.6
15
1.2
7.5
6
0.8
15
1.0
3
7
0.8
15
1.5
7
8
0.8
24
1.2
﹣﹣
①分析比较实验序号1与2与3的数据中V露随V物的变化关系及相关条件,可得出:漂浮在液面上的实心物体,当ρ液和ρ物相同时,
。
②分析比较实验序号
的数据中V露随ρ液的变化关系及相关条件,可得出的初步结论是:漂浮在不同液体中的实心物体,当ρ物和V物相同时,V露随ρ液的增大而增大。
③根据实验序号
的数据可以研究V露随ρ物的变化关系。
④实验小组同学又进一步分析了表中1~7的实验数据,发现漂浮在液面上的实心物块,V露与ρ物、V物、ρ液存在一定的定量关系,由此他们推断表中空缺的数据应该是
。
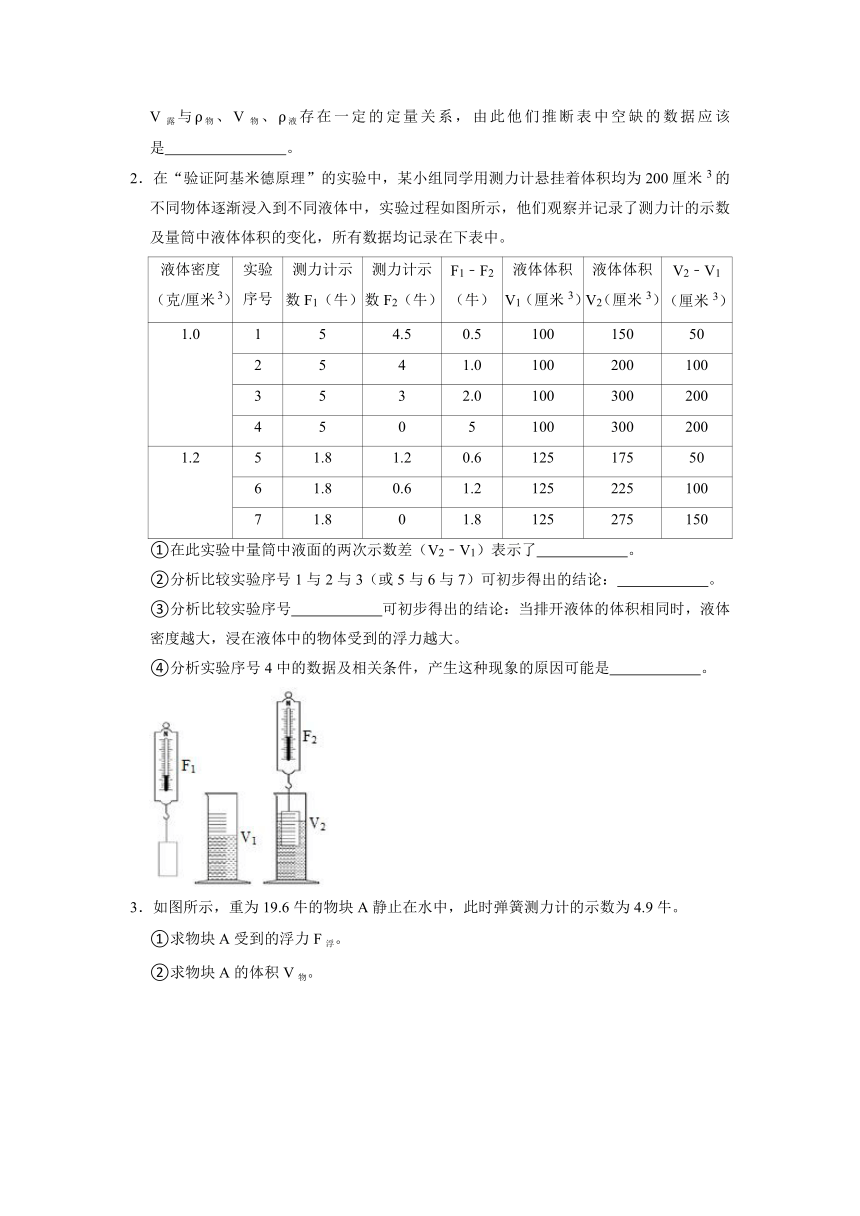
2.在“验证阿基米德原理”的实验中,某小组同学用测力计悬挂着体积均为200厘米3的不同物体逐渐浸入到不同液体中,实验过程如图所示,他们观察并记录了测力计的示数及量筒中液体体积的变化,所有数据均记录在下表中。
液体密度(克/厘米3)
实验序号
测力计示数F1(牛)
测力计示数F2(牛)
F1﹣F2(牛)
液体体积V1(厘米3)
液体体积V2(厘米3)
V2﹣V1(厘米3)
1.0
1
5
4.5
0.5
100
150
50
2
5
4
1.0
100
200
100
3
5
3
2.0
100
300
200
4
5
0
5
100
300
200
1.2
5
1.8
1.2
0.6
125
175
50
6
1.8
0.6
1.2
125
225
100
7
1.8
0
1.8
125
275
150
①在此实验中量筒中液面的两次示数差(V2﹣V1)表示了
。
②分析比较实验序号1与2与3(或5与6与7)可初步得出的结论:
。
③分析比较实验序号
可初步得出的结论:当排开液体的体积相同时,液体密度越大,浸在液体中的物体受到的浮力越大。
④分析实验序号4中的数据及相关条件,产生这种现象的原因可能是
。
3.如图所示,重为19.6牛的物块A静止在水中,此时弹簧测力计的示数为4.9牛。
①求物块A受到的浮力F浮。
②求物块A的体积V物。
4.小明同学想利用一组氮气球来提升货物(如图所示),已知他所用的轻质薄壁气球的总体积为10米3,其内部所充入的氦气密度都为0.18千克/米3
(1)求这组气球内的氮气质量m氮。
(2)求这组气球在空气中所受的浮力大小F浮(空气密度为1.29千克/米3)
(3)若忽略货物在空气中所受的浮力,求该组气球所能提升货物的最大重力Gm最大。
二.浮力大小的计算(共2小题)
5.某实心长方体在空气中称重弹簧测力计示数为24.5N,把它浸没在水中弹簧测力计示数为14.7N.求:
(1)该物体受到浮力。
(2)如该长方体的上下两表面和水面平行,它上表面受到压力为10N,求下表面所受压力。
(3)长方体的密度。
6.水平桌面上放置一轻质圆筒,筒内装有0.2米深的某液体,如图(a)所示。弹簧测力计悬挂底面积为10﹣2米2、高为0.1米的圆柱体,从液面逐渐浸入直到浸没,弹簧测力计示数F与圆柱体浸入液体深度h的关系如(b)所示。圆筒的厚度忽略不计,筒内液体没有溢出,圆柱体不碰到筒底。
①若F1=9.8牛,F2=1.96牛,求圆柱体浸没时所受浮力F浮;筒内液体的密度ρ液。
②圆柱体未浸入时筒底受到的液体压强p液。
③若轻质圆筒的底面积为2S,筒内液体深度为2h,液体密度为ρ,圆柱体底面积为S、高为h,求圆柱体浸没时,圆筒对桌面的压强p桌.(用字母表示)
三.探究影响浮力大小因素的实验(共20小题)
7.为了探究柱体A逐渐浸入柱形容器内的水中时(水没有溢出),弹簧测力计示数F的变化情况。现有底面积为100厘米2的薄壁柱形容器,容器内装有深度为20厘米的水,放在水平桌面上,实心柱体A高H为20厘米。如图所示,小明将柱体A通过细线挂在弹簧测力计下,从柱体A接触水面开始,将液面到柱体下表面的距离h、相应的弹簧测力计示数F、物体重力G与F的差值△F记录在表一中,(不计细线的重力)
表一
实验序号
1
2
3
4
5
6
7
8
h(cm)
0
2
4
6
8
10
12
14
F(N)
8
7
6
5
4
3
2
1
△F(N)
0
1
2
3
4
5
6
7
①分析比较实验序号1﹣8中F与h的变化关系及相关条件可得:同一柱体逐渐浸入柱形容器内的水中,当h小于H时,
。
②分析比较实验序号1﹣8中△F与h的变化关系及相关条件可得:同一柱体逐渐浸入柱形容器内的水中,
。
③柱体A的重力为
牛,实验序号6的实验时,A下表面所受液体压力为
牛。
④小红同学想在小明实验的基础上继续进行实验,她预设的数据如表二所示,小明看了以后认为这两次实验无法进行。
表二
实验序号
9
10
h(cm)
18
20
F(N)
﹣
﹣
△F(N)
﹣
﹣
你认为小明的观点是
的(选填“正确”或“错误”),理由是
。
8.为探究浸没在水中的物体对容器底的压力与哪些因素有关,某小组同学利用DIS数据采集系统及若干重力G和密度ρ已知的实心物体等器材进行实验。他们将实心物体放入盛水的平底容器中(如图所示),测出物体对容器底的压力F,并将实验数据记录在表一中。
表
一
实验序号
1
2
3
4
5
6
7
8
9
密度ρ(g/cm3)
2.0
2.5
3.0
重力G
(N)
4
8
12
4
8
12
3
6
9
压力F
(N)
2.0
4.0
6.0
2.4
4.8
7.2
2.0
4.0
6.0
表二
(ρ﹣ρ水):ρ
1:2
3:5
2:3
F:G
(1)分析表一中实验序号
中的数据及相关条件可初步得出:当物体的重力相同时,浸没在水中的物体对容器底的压力随物体密度的增大而增大。
(2)分析表一中实验序号1、2、3(或4、5、6,或7、8、9)中的数据及相关条件可初步得出:
。
(3)小组同学进一步综合分析表一中的数据有了新发现,他们将经计算得到的部分数据记录在表二中。
(a)表二中空缺的数据依次为
、
、
。
(b)按表二中数据反映的规律推理:若浸没在水中某实心物体的密度ρ=4g/cm3,重力G=12N,则物体对容器底的压力F=
N。
9.为了研究物体漂浮在水面上时的特点,某小组同学用甲、乙两种材料制成体积不同的若干块物块进行实验,甲材料的密度为ρ甲,乙材料的密度ρ乙,且ρ甲<ρ乙.如图所示,他们让物块漂浮在水面上,测量并记录了物块的总体积和露出水面的体积,并将实验数据记录在下表中。
材料
实验
物块体积
露出水面体积
材料
实验
物块体积
露出水面体积
序号
(10﹣6米3)
(10﹣6米3)
序号
(10﹣6米3)
(10﹣6米3)
甲
1
10
6
乙
6
8
1.6
2
20
12
7
10
2
3
30
18
8
30
6
4
40
24
9
35
7
5
50
30
10
45
9
①分析比较实验序号
数据,可得出的初步结论是:同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比。
②分析比较实验序号1与7、3与8的数据,可得出的初步结论是:
。
③他们分别分析了“露出水面的体积”和“物体体积”的比例关系,可以得出的进一步结论是:
(a)
。
(b)
。
10.为研究物体在液体中受到向上的力与哪些因素有关,小明设计了方案进行实验。小明用弹簧测力计将一圆柱体悬挂在空容器中,如图所示,此时弹簧测力计的示数为F0,然后逐次向容器中注入液体A,并将圆柱体下表面到液面的距离h、相应的弹簧测力计示数F、F0与F的差值△F记录在表一中。为进一步探究,小明换用液体B重复实验,并将数据记录在表二中。(液体A、B密度分别为ρA、ρB,且ρA>ρB)
表一(液体A)
表二(液体B)
实验序号
h(厘米)
F(牛)
△F(牛)
实验序号
h(厘米)
F(牛)
△F(牛)
1
3.0
8.5
1.5
5
3.0
8.8
1.2
2
6.0
7.0
3.0
6
6.0
7.6
2.4
3
9.0
5.5
4.5
7
9.0
6.4
3.6
4
12.0
5.0
5.0
8
12.0
6.0
4.0
①分析比较实验序号1、2与3(或5、6与7)数据中F和h的关系及相关条件,可得初步结论:
同一物体在同一种液体中,
。
②分析比较实验序号1、2与3(或5、6与7)数据中△F和h的关系及相关条件,可得初步结论:
同一物体在同一种液体中,
。
③分析比较实验序号1、5(或2、6,或3、7)数据中△F和h的关系及相关条件,可得初步结论是:
同一物体在
。
④实验中圆柱体重力为
牛,高度为
厘米。
11.小徐和小汇在学习“浮力”时,根据生活经验,对物体受到浮力的大小与哪些因素有关提出猜想并进行了研究。
①根据鸡蛋在水中沉底、在盐水中漂浮的现象,他们猜想浮力的大小可能与
有关。根据游泳时的感觉,他们猜想浮力的大小可能与物体浸入液体的深度,以及物体浸入液体的体积有关。
②为了验证猜想,他们用压力传感器将一长方体金属块悬挂在空量筒中,如图所示,然后逐次向容器中注入液体A,测出金属块下表面到液面的距离即金属块浸入液体的深度h,计算出金属块浸入液体的体积V和金属块受到的浮力F,把实验数据记录在表一中。为了进一步探究,他们还换用了液体B重复实验,并把实验数据记录在表二中。(液体A、B密度分别为ρA、ρB,ρA>ρB)
表一:将金属块浸入液体A中
实验序号
浸入的深度h(厘米)
浸入的体积V(厘米3)
浮力F(牛)
1
2.0
12
0.12
2
6.0
36
0.36
3
10.0
60
0.60
4
15.0
60
0.60
表二:将金属块浸入液体B中
实验序号
浸入的深度h(厘米)
浸入的体积V(厘米3)
浮力F(牛)
5
2.0
12
0.10
6
6.0
36
0.30
7
10.0
60
0.50
8
15.0
(a)小汇分析比较实验序号1、2、3的F和V、h的数据后,得出初步结论:同一物体浸入同一液体中,F与V成正比,而且F与h成正比。
小徐分析比较实验序号
的数据,认为小汇的结论存在问题,请写出小徐观点的依据
。
(b)请补全实验序号8中的数据。
、
。
(c)他们分析比较表一和表二中的数据,得出结论:同一物体浸入不同液体中:
。
③他们交流后,认为上述得出的结论还不够完善,需要增加一次实验进行论证,下列方案中你建议采用方案
。
A.仍用上述金属块,浸入密度不同的液体C中,重复实验
B.仍用上述金属块,增加金属块浸入液体A或B中的深度进行实验
C.换用其他物质(如其他材质的金属块),仍在液体A或B中进行实验
12.某小组同学研究当圆柱体浸入水中时,容器底部受到水压力的增加量和圆柱体所受浮力大小的变化情况。实验选用由上、下两个横截面积不同的圆柱形构成的容器,如图所示。实验时将重为8.0牛的圆柱体缓慢浸入水中,将圆柱体下表面到水面的距离h、弹簧测力计的示数F1、容器底部受到水的压力F2记录在如表中,并计算出相应的浮力F浮和水对容器底部压力的增加量△F水。
实验序号
h(厘米)
F1(牛)
F2(牛)
F浮(牛)
△F水(牛)
1
0
8.0
12.0
0
0
2
0.5
7.8
12.2
0.2
0.2
3
1.0
7.6
12.4
0.4
0.4
4
1.5
7.4
12.6
0.6
0.6
5
2.0
7.2
13.0
0.8
1.0
6
2.5
7.0
13.7
1.0
1.7
7
3.0
6.8
14.4
1.2
2.4
8
3.5
6.6
15.1
1.4
3.1
9
4.0
6.6
15.1
1.4
3.1
①分析比较实验序号2~7数据中△F水与h的变化关系,可得出的初步结论是:在圆柱体浸入水的过程中,
;
②分析比较实验序号2~7数据中F浮与h的变化关系,可得出的初步结论是:在圆柱体浸入水的过程中,
;
③分析比较实验序号8和9数据发现,△F水、F浮不再随h的变化而变化,其原因是
;
④该组同学分析实验序号2~4数据可得出的结论是:在圆柱体浸入水的过程中,△F水与F浮大小相等。但实验序号5~9数据与上述结论不符,其原因是
;
⑤请根据实验数据推断:组成容器的上、下两部分圆柱形的横截面积之比为
。
13.小华做“验证阿基米德原理”的实验中,用图(a)所示的溢杯和小桶收集石块排开的水,他的实验过程分别如图(b)、(c)、(d)、(e)所示。
(1)图(c)所示,是小华在使用
测量石块的
。
(2)若图中四个测量值F1、F2、F3、F4满足关系式
,该原理将得到验证。
(3)以下关于实验过程中的操作,会影响验证结果的是
。
A.图(a)中溢杯内未盛满水。
B.图(b)中小桶内有少量水。
C.图(d)中石块未浸没水中。
14.某兴趣小组在学习浮力时,将一底面积为0.01米2的轻质柱形溢水杯放置于台秤上,并在溢水杯内装入适量水。然后,用测力计悬挂一柱形合金块慢慢浸入水中,实验过程如图所示。他们记录了合金块下表面到溢水杯底部的距离h、测力计示数F1、台秤示数F2,实验数据如表所示。请根据表格中相关信息,回答下列问题。(本题g取10牛/千克)
实验序号
1
2
3
4
5
6
7
h
(米)
0.15
0.14
0.12
0.11
0.09
0.08
F1(牛)
11.5
10.5
8.5
8.0
7.5
7.5
6.5
F2
(牛)
17.0
18.0
20.0
20.0
20.0
20.0
21.0
(1)从实验序号
开始,溢水杯内水面不再上升;在整个实验过程中,共溢出水
牛。
(2)请完成序号7空缺数的填写。
(3)该合金块的密度是
千克/米3。
15.某小组同学用如图所示装置,研究圆柱体在水中下降的过程中弹簧测力计示数和台秤示数的变化情况。他们使圆柱体在水中缓慢下降,将圆柱体下表面到水面的距离h、弹簧测力计的示数F1、台秤的示数F2记录在下表中。
实验序号
h(厘米)
F1(牛)
F2(牛)
1
1.0
7.7
10.3
2
2.0
7.4
10.6
3
3.0
7.1
10.9
4
4.0
6.8
11.2
5
5.0
6.5
11.5
6
6.0
6.5
11.5
①分析比较实验序号1~4的数据中F1、F2的变化情况及相关条件,可得出的初步结论是:圆柱体在浸入水的过程中,F1
,F2
;
②表中实验序号
的数据表明,圆柱体在相应的位置已全部浸没在水中;
③表中两组数据间F1变化量的大小为△F1,相应的F2变化量的大小为△F2,分析比较实验序号1~6的数据,可得出的结论是:圆柱体在水中缓慢下降的过程中,△F1与△F2的关系是
。当圆柱体处于实验序号6的位置时,所受浮力的大小为
牛。
16.甲、乙、丙三个小组同学发现如图(a)所示的驳船底部设计得比较宽大。于是,他们想“探究驳船的底部到液面的深度与哪些因素有关”。实验时,他们用圆柱体来模拟驳船,并选取了密度不同的三种液体来模拟不同密度的水域,将质量和底面积大小不同的圆柱体分别放入液体中,每次都使圆柱体漂浮在液面上,如图(b)所示。实验过程中,他们测量了所用圆柱体的质量m、底面积S和它的底部到液面的深度h,所有数据均记录在下表中。
序号
小组
容器中液体的密度ρ(×103千克/米3)
圆柱体的质量m
(千克)
圆柱体的底面积S(10﹣2米2)
深度h(米)
1
甲
0.8
0.06
0.05
0.15
2
0.8
0.12
0.06
0.25
3
0.8
0.12
0.05
0.30
4
乙
1.0
0.12
0.06
0.20
5
1.0
0.25
0.10
0.25
6
1.0
0.30
0.10
0.30
7
丙
1.2
0.12
0.10
0.10
8
1.2
0.12
0.05
0.20
9
1.2
0.30
0.10
0.25
①分析比较实验序号1与3(或5与6或7与9)的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体底面积S和液体密度ρ相同时,
。
②分析比较实验序号2与3(或7与8)的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,
。
③分析比较实验序号
的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体的质量m和底面积S相同,液体密度ρ越大,圆柱体的底部到液面的深度h越小。
④三个小组的同学对表格中的数据计算之后,进一步综合归纳结论,
a.分析比较实验数据2、5与9或3与6或4与8可归纳得出的结论是:漂浮在液面上的圆柱体,
,圆柱体的底部到液面的深度h相同。
b.分析比较实验数据2、5与9和3与6和4与8可归纳得出的结论是:漂浮在液面上的圆柱体,
。
⑤通过上述研究的过程,同学们明白了驳船载重小并且底部设计比较宽大,主要是为了减少
,避免搁浅的发生。
17.小明将六个体积相同、重力G不同的正方体物块放入水中(ρ物<ρ水),研究浮在水中的物块浸入水中的体积V浸的情况。实验时,他将物块放入同一个盛有水的大容器中,然后对物块施加竖直向下的压力F,待物块静止后,观察物块浸入水中的体积V浸.相关实验数据和现象如下表所示。
实验序号
1
2
3
4
5
6
放入物块的重力G(牛)
3
6
3
6
3
6
竖直向下的压力F(牛)
3
3
6
6
9
9
实验现象
①观察序号1与2或3与4或5与6中的实验现象并分析V浸和G、F的关系,可初步归纳得出的结论是:浮在水面上的物块,
。观察序号
的实验现象并分析V浸和G、F的关系,可得出的初步结论是:浮在水面上的物块,当物块所受重力G相同时,F越大,V浸越大。
②综合分析表中的实验现象及相关数据,进一步归纳结论。
(a)观察实验序号2与3或4与5中的实验现象并分析V浸和G、F的关系,可得出:浮在水面上的物块,
,V浸相同。
(b)观察实验序号2与3和4与5中的实验现象并分析V浸和G、F的关系,可得出:浮在水面上的物块,
。
18.为了探究物体受到的浮力F浮与物体体积V物有关还是与物体浸入液体的体积V浸有关,某小组同学设计方案进行探究。
物体
A
B
C
体积
4V
2V
V
①现有可供选择的物体如下表所示,在研究F浮与V物的关系时应选择
物体(选题“一个”或“多个”),并控制其浸入水中的体积
(选填“相同”或“不同”),测出其受到的浮力。
②该小组同学经过讨论完善方案后继续实验,将体积不同的物体浸入水中,测出物体受到的浮力,实验现象和数据如下表所示。
实验序号
1
2
3
4
5
实验示意图
V物(米3)
0.4×10﹣3
0.2×10﹣3
V浸(米3)
0.1×10﹣3
0.2×10﹣3
0.4×10﹣3
0.1×10﹣3
0.2×10﹣3
F浮(牛)
1
2
4
1
2
根据序号
的实验示意图及数据,可得F浮与V物无关。
根据序号1和2和3中的实验示意图及是数据,可得出的初步结论是:同一物体浸入水中,
。
③他们尝试利用液体内部压强知识阐述浮力产生的原因,当物体浸没在液体中时,如图1所示:
F浮=F2﹣F1=p2S﹣p1S=p液gh2S﹣p液gh1S=p液g(h2﹣h1)S=p液gV物
当物体部分浸入液体中时,如图2所示,请利用液体内部压强知识推导出物体受到的浮力。
。
19.为了探究漂浮在液面上的物块露出液面的体积V露与物块密度ρ物、液体密度ρ液的关系,某小组同学选取体积V物相同、ρ物不同的物块进行实验,测出其漂浮在水和酒精液面上时露出液面的体积V露,相关数据记录在表一、表二中。
表一:水
ρ液(克/厘米3)
实验序号
ρ物(克/厘米3)
V浸(厘米3)
1.0
1
0.4
40
2
0.5
50
3
0.6
60
表二:酒精
ρ液(克/厘米3)
实验序号
ρ物(克/厘米3)
V浸(厘米3)
0.8
4
0.4
50
5
0.5
62.5
6
0.6
75
表三
第一组
ρ液=1.0克/厘米3ρ物=0.2克/厘米3
ρ液=1.5克/厘米3ρ物=
克/厘米3
第二组
ρ液=1.0克/厘米3ρ物=
克/厘米3
ρ液=1.5克/厘米3ρ物=0.6克/厘米3
①分析比较表一或表二中ρ物、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上的物块,
。
②分析比较实验序号
中,ρ液、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上的物块,当V物、ρ物相同时,ρ液越小,V露越小。
③由实验序号2与4的数据及相关条件,发现漂浮在液面上V物相同的物块,存在与ρ液均不同而V露相同的现象。若用V物相同的物块进一步实验,请在表三中填入拟进行实验的数据,使每一组实验均能研究上述现象。
20.在探究“影响浮力大小的因素”这一问题时,请你根据图中实验操作,从中选出一些图,针对某一个因素进行探究,并通过分析弹簧测力计的示数,说明你的探究结果。
(1)探究的因素是:浮力大小与物体排开液体体积;选用的图是:
(填图中序号);探究的结果是:物体排开液体体积越大,浮力越大。
(2)探究的因素是:
;选用的图是:(a)、(d)、(e);探究的结果是:
。
(3)上述所设计的方案,采用的科学方法是
法。
21.为了探究漂浮在液面上的均匀实心正方体物块露出液面的高度h与哪些因素有关,某小组同学进行了讨论并形成了两个猜想,猜想(一)认为h的大小可能与液体的密度有关猜想(二)认为h的大小可能与正方体物块的密度ρ物有关。为此,他们与老师一起设计了探究方案如下:
探究步骤(一):探究h与液体密度ρ液的关系
1.测出正方体物块的边长H。
2.将这个正方体物块分别漂浮于不同液体中,测出相应的h值。
3.记录数据并归纳总结结论。
探究步骤(二):探究h与
的关系
1.选用不同密度的若干正方体物块,要求它们的边长相等,测出边长H。
2.将不同密度的正方体物块分别漂浮于水面上,测出相应的h值。
3.设计记录数据表如表一所示:
表一
实验序号
物块的密度ρ物(千克/立方米)
水的密度ρ液(千克/立方米)
h(厘米)
H(厘米)
1
2
3
…
…
…
…
…
4.记录数据并归纳总结结论。
探究步骤(三):进一步综合分析并归纳总结结论。
①你认为探究步骤(一)中需要改进的地方是什么?答:
。
②请你填写完整“探究步骤(二):探究h与
的关系”。
③该小组同学在完善方案后进行了实验探究活动,其中实验步骤(二)收集到的数据如表二所示;
表二
实验序号
物块的密度(千克/立方米)
水的密度(千克/立方米)
h(厘米)
H(厘米)
1
400
1000
6
10
2
600
1000
4
10
3
800
1000
2
10
…
…
…
…
…
根据实验序号1与2与3,初步分析可得出的结论是:漂浮在水面上的物块,
。
④根据表二的数据可以推测:若露出水面的高度为零时,物块的密度ρ物与水的密度ρ水的比值等于
。
⑤关于正方体物块露出液面的高度h与它的边长H的比值,正确的是
。
A.
B.
C.
D.
22.小明和小华两位同学通过实验研究圆柱体浸入液体(足够深)的过程中测力计示数F的变化情况。如图所示,他们将高H为10厘米的圆柱体A挂在测力计下,逐步改变其下表面到液面的距离h,读出相应的测力计示数F,将h、F、及每一次实验中F的变化量△F记录在表一中。然后,他们变换液体重复实验,将数据记录在表二中。(已知ρ1<ρ2)
表一(液体密度为ρ1)
实验序号
h(厘米)
F(牛)
△F(牛)
1
0
22.0
0
2
1
21.2
0.8
3
4
18.8
3.2
4
8
15.6
6.4
5
10
14.0
8.0
6
14
14.0
8.0
表二(液体密度为ρ2)
实验序号
h(厘米)
F(牛)
△F(牛)
7
0
22.0
0
8
1
21.0
1.0
9
4
18.0
4.0
10
8
14.0
8.0
11
10
12.0
10.0
12
14
12.0
10.0
①分析比较实验序号2与3与4(或8与9与10)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入同种液体过程中,
。
②分析比较实验序号2与8(或3与9或4与10或5和11)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入不同液体过程中,
。
③小明和小华继续分析表一、表二数据中F和h的关系,并进行相关思考。
(a)分析比较实验序号1~5(或7~11)数据中F和h的关系及相关条件,可得出的初步结论是:
。
(b)分析比较实验序号5和6(或11和12)数据中F和h的关系及相关条件,小明认为:“当h满足一定条件时,F不再随h的变化而变化。”为验证该观点,他们换用高H为15厘米的圆柱体B继续实验,初步证明小明正确。表三记录了他们的部分实验数据,请将表三中的数据填写完整。
表三(液体密度为ρ1)
实验序号
h(厘米)
F(牛)
13
15
14
17
20.0
15
20
23.某小组同学通过实验探究盛有液体的容器在放入物体前、后容器底部受到液体压力的增加量△F液与哪些因素有关。
①他们猜想:△F液与放入物体的重力G物有关,于是选用重力不同而体积相同的物体和水进行实验。他们将物体先后放入同一盛有水的容器中,并测得容器底部受到水的压力增加量△F水.实验示意图及相应数据见表一。
表一
实验序号
1
2
3
实验示意图
G物(牛)
2.0
2.4
2.8
△F水(牛)
1.0
1.0
1.0
分析比较表一中△F水和相关条件,可得:△F水与G物
(选填“有关”或“无关”)。
②他们提出新的猜想:△F水与放入物体的体积V物有关,于是选择不同物体先后放入盛有相等质量水的相同容器中,待物体静止,测得△F水.实验示意图及相应数据见表二。
表二
实验序号
4
5
6
7
8
现象
V物(×10﹣4米3)
0
0.9
1.2
1.4
1.4
1.4
△F水(牛)
0
0.9
1.2
1.4
1.2
1.0
他们首先分析比较了实验序号4与5与6,得到:△F水与V物有关,且
。接着,他们全面分析后,比较了实验序号
,发现:△F水与V物无关。他们交流讨论后,分析比较了实验序号6与7与8,得到:影响△F水的因素可能是
,继续研究,还应选用
完成实验。
24.小同学选用弹簧测力计、
和系细绳的金属块各一个,及三种密度不同液体进行如图所示实验,设计的实验表格如下。小李同学将测得数据及根据数据计算得到的结果记录在表中(部分未显示)。
实验序号
ρ(×103千克/米3)
V1(×10﹣3米3)
V2(×10﹣3米3)
F1(牛)
F2(牛)
F1﹣F2(牛)
ρg(V2﹣V1)
1
1.2
4.0
2.8
1.2
2
1.0
4.0
3.0
1.0
3
0.8
4.0
3.2
0.8
①填写
所对应的器材,该金属块所受重力为
。
②分析实验数据并得出初步结论:
a.分析比较实验序号1与2中ρ和F2数据及相关条件可初步得出结论,对浸没在液体中的同一金属块而言,
。
b.分析比较实验序号1、2、3中ρ和F1﹣F2数据及相关条件可初步得出结论,对浸没在液体中的同一金属块而言,
。
③根据小李同学所设计的表格和实验步骤,该实验的实验目的应该是
(填写选项序号“A”“B”“C”或“D”)。
A.验证阿基米德原理
B.探究物体所受浮力与哪些因素有关
C.探究物体所受浮力与体积的关系
D.练习使用弹簧测力计测物体所受浮力
④为使实验结论更有普遍性,请提出补充设计建议
。
25.小明同学研究圆柱体在某种液体中下降的过程中,圆柱体上、下表面受到液体的压力大小F1和F2与圆柱体下表面浸没在液体中深度h的关系,如图所示。小明使高为0.2米的实心圆柱体在液体中缓慢下降,测量出圆柱体下表面到液面的深度h、利用仪器测出圆柱体上、下表面处液体的压强,利用公式求得圆柱体上、下表面受到液体的压力F1和F2,进一步计算圆柱体下表面与上表面受到液体的压力差△F,记录在下表中。
实验序号
h(米)
F1(牛)
F2(牛)
△F(牛)
1
0.18
a
18.0
2
0.20
b
20.0
3
0.22
2.0
22.0
20.0
4
0.24
4.0
24.0
20.0
5
0.26
6.0
26.0
20.0
①a、b分别为
和
。
②分析比较实验序号1~5数据中,F2与h的关系及相关条件,可得出的初步结论是:
。
③分析比较实验序号3与4与5数据中,△F与h关系及相关条件,可得出的初步结论是:
。
④如果进一步研究圆柱体浸没在液体中,圆柱体下表面受到液体的压力大小与液体密度的关系。实验方案中应该控制不变的物理量为:
(选填“圆柱体下表面在液体中的深度”或“液体密度”)
26.小林和小徐通过实验研究将物体浸入液体的过程中,容器对水平桌面压力的变化情况。如图18所示,他们将重力分别为30牛、40牛的甲、乙两个柱形物体,先后挂在弹簧测力计下,并将其逐渐浸入放在水平桌面上的同一柱形容器的液体中(液体不溢出)。他们读出测力计示数F,并测得容器对桌面的压力F桌,并根据相关物理量计算出物体所受浮力F浮,将数据记录在表一、表二中。
实验序号
F(N)
F浮(N)
F桌(N)
1
20
10
60
2
16
14
64
3
12
18
68
4
8
22
72
5
4
22
76
表二
物体乙的重为40N
实验序号
F(N)
F浮(N)
F桌(N)
6
30
10
60
7
25
15
65
8
18
22
72
9
10
30
80
10
8
30
①小林分析比较实验序号
后得出结论:不同柱形物体浸入同一柱形容器液体中时,物体所受浮力相同,容器对桌面压力相同。
②分析表一、表二中实验序号5与8的数据与小林得出结论不符的原因
。
③小徐分析比较实验序号1、2、3、4(或6、7、8、9)F桌变化量与F浮变化量的关系后得出初步结论:
。
④进一步分析表一和表二的数据,可得实验序号10的F桌的大小为
牛。
四.物体的浮沉条件及其应用(共4小题)
27.为了探究漂浮在液面上的物块露出液面的体积V露与物块密度ρ物、液体密度ρ液的关系,某小组同学选取体积相同、ρ物不同的物块进行实验,测出其漂浮在水和酒精液面上时露出液面的体积V露,相关数据记录在表一、表二中。
表一:水
实验序号
ρ液(克/厘米3)
ρ物(克/厘米3)
V露(厘米3)
1
1.0
0.4
60.0
2
0.5
50.0
3
0.6
40.0
表二:酒精
实验序号
ρ液(克/厘米3)
ρ物(克/厘米3)
V露(厘米3)
4
0.8
0.4
50.0
5
0.5
37.5
6
0.6
25.0
(1)分析比较表一或表二中ρ物、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上体积相同的物块,
。
(2)分析比较实验序号
中ρ液、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V露越小。
(3)由实验序号2与4的数据及相关条件,发现漂浮在液面上体积相同的物块,存在ρ物与ρ液均不同而V露相同的现象。若用其它体积相同的物块进一步实验,请在表三中填入拟进行实验的数据,使每一组实验均能研究上述现象。
表三:密度值(克/厘米)
第一组
ρ液=1.0ρ物=0.2
ρ液=1.5ρ物=
第三组
ρ液=1.0ρ物=
ρ液=1.5ρ物=0.6
28.把一个外观体积为17.8cm3的空心铜球放入水中,它恰好处于悬浮状态。已知铜的密度是8.9×103kg/m3,g取10N/kg,求:
(1)空心铜球的重力;
(2)铜球空心部分的体积。
29.抹香鲸是世界上最大的齿鲸,它在所有鲸中潜水最深且最久,号称“潜水冠军”,如图所示。一头体长19米,体积24米3的成年抹香鲸可轻松潜至1000米深的海底。
(1)求潜至此深度时,抹香鲸所受到的浮力大小F浮。
(2)若抹香鲸继续下潜至2000米深的海底,它受到的浮力会变化吗?为什么?
(假设海水密度为1×103千克/米3,且不随深度变化)
30.如图所示,装水的圆柱形玻璃容器汇总漂浮着质量为0.2千克的苹果,已知容器的底面积为0.01米2。
求:(1)苹果受到的浮力;
(2)苹果排开水的体积;
(3)若将苹果缓慢从容器中取出(苹果带出的水忽略不计),则容器底受到水的压强变化了多少?
参考答案
一.阿基米德原理的应用(共4小题)
1.【解答】解:①分析比较实验序号1与2与3的数据中V露随V物的变化关系及相关条件可知,物体的密度和液体的密度是相同的,物体都漂浮在液面上,物体的体积越大,物体漏在液面外的体积越大,所以结论为:漂浮在液面上的实心物体,当ρ液和ρ物相同时,露随V物的增大而增大;
②探究V露与ρ液的关系时需要控制物体都处于漂浮状态,物体的密度和物体的体积都相同,改变液体的密度,所以应该分析比较实验序号4与5或6和7的数据,根据数据可知,当ρ物和V物相同时,V露随ρ液的增大而增大;
③研究V露随ρ物的变化关系时,根据控制变量法可知,需要控制物体漂浮,液体的密度不变,物体的体积不变,改变物体的密度,所以需要对比2与6的实验数据;
④根据实验序号1可知:==;==;
根据实验序号2可知:==;==;
……
根据实验序号5可知:==;==;
……
根据实验序号7可知:==;==;
由此可知,=1﹣;
第8组数据中:=1﹣,代入数据得:=1﹣,解得:V露=8×10﹣6m3。
故答案为:①V露随V物的增大而增大;②4与5或6和7;③2与6;④8。
2.【解答】解:
(1)在验证阿基米德原理的实验中,根据称重法可知,(F1﹣F2)表示浸在液体里的物体所受浮力,(V2﹣V1)表示排开液体的体积;
(2)分析比较实验序号1与2与3(或5与6与7)的实验数据可初步得出的结论为:当液体密度相同时,物体受到的浮力与排开液体的体积成正比,排开液体的体积越大,物体受到的浮力越大;
(3)从表中数据可知,序号为1与5的实验中排开液体的体积都是50cm3,第5次实验中液体的密度大于第1次实验中液体的密度,第5次实验物体受到的浮力较大,符合题目要求,
同理,实验序号2和6的数据也符合要求;
(4)在第4次实验中,F2为0,说明弹簧测力计没有提起物体,可能是物体碰到了容器底部。
故答案为:(1)排开液体的体积;
(2)当液体密度相同时,物体受到的浮力与排开液体的体积成正比,排开液体的体积越大,物体受到的浮力越大;
(3)1与5(或2与6);
(4)物体碰到了量筒底部。
3.【解答】解:(1)该物体A受到的浮力:
F浮=G﹣F=19.6N﹣4.9N=14.7N;
(2)根据F浮=ρ液gV排可得排开水的体积:
V排===1.5×10﹣3m3;
由于物体处于浸没状态,则物块A的体积V物=V排=1.5×10﹣3m3。
答:①物块A受到的浮力F浮=14.7N。
②物块A的体积V物=1.5×10﹣3m3。
4.【解答】解:(1)由ρ=可得,这组气球内的氮气质量:
m氮=ρ氮V氮=ρ氮V气球=0.18kg/m3×10m3=1.8kg;
(2)这组气球在空气中所受的浮力:
F浮=ρ空气gV排=ρ空气gV气球=1.29kg/m3×10N/kg×10m3=129N;
(3)若忽略货物在空气中所受的浮力,且轻质气球本身的质量可忽略,
则该组气球所能提升货物的最大重力:
Gm最大=F浮﹣G氮=F浮﹣m氮g=129N﹣1.8kg×10N/kg=111N。
答:(1)这组气球内的氮气质量为1.8kg;
(2)这组气球在空气中所受的浮力为129N;
(3)若忽略货物在空气中所受的浮力,该组气球所能提开货物的最大重力为111N。
二.浮力大小的计算(共2小题)
5.【解答】解:(1)根据题意可知,长方体的重力G=24.5N,长方体浸没在水中时弹簧测力计示数F′=14.7N,
则该物体在水中受到的浮力:
F浮=G﹣F′=24.5N﹣14.7N=9.8N;
(2)根据F浮=F向上﹣F向下可知:
下表面所受压力F向上=F浮+F向下=9.8N+10N=19.8N;
(3)由于长方体浸没时排开液体的体积和本身的体积相等,
由F浮=ρgV排可得,该长方体的体积:
V=V排===1×10﹣3m3;
则长方体质量:
m===2.5kg,
长方体密度:
ρ===2.5×103kg/m3。
答:(1)该石块浸没在水中时受到的浮力为4.9N;
(2)下表面所受压力为19.8N;
(3)该长方体的密度为2.5×103kg/m3。
6.【解答】解:①由图象知,当h=0时,此时测力计的示数等于圆柱体的重力,所以G=F1=9.8N;
当深度为h时,测力计的示数不变,说明圆柱体完全浸没;F2=1.96N,
所以F浮=F1﹣F2=9.8N﹣1.96N=7.84N;
物体排开液体的体积V排=V物=10﹣2m3×0.1m=1×10﹣3m3
由F浮=ρ液gV排得,
ρ液===0.8×103kg/m3
②圆柱体未浸入时h液=0.2m,
筒底受到的液体压强p液=ρ液gh液=0.8×103kg/m3×9.8N/kg×0.2m=1568Pa;
③液体的质量m液=ρV液=ρ2S×2h=4ρSh,
G液=m液g=4ρShg,
圆柱体浸没时,F浮=ρ液gV排=ρgSh,
所以,对桌面的压力F桌=G液+F浮=4ρShg+ρgSh=5ρgSh,
∴压强p桌===2.5ρgh。
答:①圆柱体浸没时所受浮力F浮=7.84N;筒内液体的密度ρ液=0.8×103kg/m3;
②圆柱体未浸入时筒底受到的液体压强p液=1568Pa;
③圆筒对桌面的压强p桌=2.5ρgh。
三.探究影响浮力大小因素的实验(共20小题)
7.【解答】解:①实心柱体A高H为20cm,从柱体A接触水面开始到液面到柱体下表面深度为14cm时,弹簧测力计示数F逐渐变小,得到的结论:同一柱体逐渐浸入柱形容器内的水中,当h小于H时,液面到柱体下表面越深,弹簧测力计示数越小。
②由表一数据知,物体重力G与F的差值△F与液面到柱体下表面的距离h的比值是0.5N/cm,说明物体重力G与F的差值△F与液面到柱体下表面的距离h成正比。
③由第一次实验数据知,实心柱体刚刚接触水面,弹簧测力计测量柱体重力大小,重力大小是8N。
物体重力G与F的差值△F实际上是水对柱体的浮力,浮力大小等于水对柱体向上和向下的压力差,此时柱体没有浸没,水对柱体向下的压力为零,所以浮力大小等于水对柱体向上的压力,即F压=△F=5N。
④根据②中分析知,△F与液面到柱体下表面的距离h的比值是0.5N/cm,当h=16cm时,△F为8N,浮力等于重力,柱体在h=16cm时,柱体就漂浮在水面上,当h=18cm,h=20cm时,弹簧测力计是都没有示数,所以小明认为实验无法进行,小明的观点是正确的。
故答案为:①液面到柱体下表面越深,弹簧测力计示数越小;②重力和弹簧测力计的差值与液面到柱体下表面的距离成正比;③8;5;④正确;当h=16cm时,柱体已经漂浮在水面上,h>16cm时,弹簧测力计示数都为零。
8.【解答】解:(1)1与4、2与5、3与6的重力相同,物体的密度不同,且密度越大,压力越大,可得当物体的重力相同时,浸没在水中的物体对容器底的压力随物体密度的增大而增大;
(2)1、2、3(或4、5、6,或7、8、9)中的数据,压力与重力的比值相同,为一定值,可得当物体的密度相同时,浸没在水中的物体对容器底的压力与物体的重力成正比;
(3)(a)经计算得,第一组F与G的比值为1:2,第二组F与G的比值为3:5,第三组F与G的比值为2:3;
(b)ρ=4g/cm3,则(ρ﹣ρ水):ρ==3:4,
由表格中数据知,F:G=(ρ﹣ρ水):ρ,所以F:G=3:4,则F=×12N=9N。
故答案为:(1)1与4(或2与5,或3与6);(2)当物体的密度相同时,浸没在水中的物体对容器底的压力与物体的重力成正比;(3)(a)1:2;3:5;2:3;(b)9。
9.【解答】解:①1、2、3、4、5或6、7、8、9、10都是同种材料,由1、2、3、4、5数据可知,露出水面的体积与物块的体积比值总等于3:5,6、7、8、9、10的数据可知,露出水面的体积与物块的体积比值总等1:5,可得同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比;
②序号1与7、3与8的数据,物体的材料不同,体积相同,甲的密度较小,露出水面的体积较大,乙的密度较大,露出水面的体积较小,可得体积相同的不同材料的物块漂浮在水面上,材料密度小的物块,露出水面的体积大;
③(a)对于甲材料制成的物体,露出水面体积与物体体积的比值都是3:5,对于乙材料制成的物体,露出水面体积与物体体积的比值都是1:5,可得同种材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例相等;
(b)甲材料的密度小于乙材料的密度,但得出露出水面的体积与物体体积的比例大于乙材料露出水面的体积与物体体积的比例。
故答案为:①1、2、3、4、5或6、7、8、9、10;②体积相同的不同材料的物块漂浮在水面上,材料密度小的物块,露出水面的体积大;③(a)同种材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例相等;(b)不同材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例不相等,且材料密度大的比例小。
10.【解答】解:①根据实验序号1与2与3或5与6与7的数据,分析比较弹簧测力计的示数F与圆柱体的下表面到液面的深度h的大小关系,可得出的初步结论是:同一物体在同种液体中,弹簧测力计示数F随圆柱体的下表面到液面的深度增大而减小;
②纵向比较表一序号1与2与3或表二序号5与6与7的数据,可知,圆柱体的下表面到液面的深度h为原来的几倍,△F也为原来的几倍,可得出的初步结论是:同一物体在同种液体中,△F与圆柱体的下表面到液面的深度h成正比;
③ρA=1.0×103kg/m3>ρB=0.8×103kg/m3,
根据实验序号1与5或2与6或3与7的数据,可得出的初步结论是:同一物体在不同液体中,圆柱体的下表面到液面的深度h不变时,液体密度ρ越大,△F越大;
④F0=G,根据称重法测浮力,△F=F0﹣F,
故本实验中,圆柱体的重力为:G=△F+F=1.5N+8.5N=10.0N;
由②,比较表一序号1与2与3或表二序号5与6与7的数据,可知同一物体在同种液体中,△F与圆柱体的下表面到液面的深度h成正比;但序号4与8实验不符合这个规律;
根据阿基米德原理,F浮=ρ液gV排,在物体没有浸没时,F浮=ρ液gSh,故受到的浮力与圆柱体的下表面到液面的深度h成正比,
浸没在液体中的物体受到的浮力与深度无关,说明4与8这两种情况下,圆柱体已浸没在液体中了,
由阿基米德原理:
1、4两次实验受到的浮力之比为:=,则:h=×3cm=10cm。即圆柱体的高度为10.0厘米。
故答案为:①弹簧测力计示数F随圆柱体的下表面到液面的深度增大而减小;②△F与圆柱体的下表面到液面的深度h成正比;③同一物体在不同液体中,圆柱体的下表面到液面的深度h不变时,液体密度ρ越大,△F越大;④10.0;10。
11.【解答】解:①先使鸡蛋在两种液体中浸没,根据控制变量法,鸡蛋排开液体的体积不变,而水与盐水的密度不同,鸡蛋在盐水中上浮(后漂浮),在水中沉底,所以浮力大小与液体密度有关;
②(a)分析表一实验序号3、4的数据,同一物体浸入同一液体中,当浸入液体体积相同时,浮力F不变,与h不成正比;
(b)根据表一得出得结论:同一物体浸入同一液体中,当浸入液体体积相同时,浮力F不变,与h无关,所以对比表二实验序号7,得出实验序号8的数据:浸入体积V=60厘米3,浮力F=50N;
(c)分析比较表一和表二中的数据,实验序号1、5(或2、6,或3、7),得出结论:同一物体浸入不同液体中,浸入相同体积,所受浮力不同;
③为了使实验结论具有普遍性,防止偶然性,换用其他物质(如其他材质的金属块),仍在液体A或B中进行实验;
A选项变化的量是液体密度,在上述实验序号1、5(或2、6,或3、7)已经探究过,故不合题意;
B选项变化的量是浸入的深度,在表一实验序号3、4已经探究,故不合题意;
C选项变化的量是固体的密度,前面的实验中没有探究,所以实验有意义,符合题意;故选C。
故答案为:①液体的密度;
②(a)3、4;同一物体浸入同一液体中,当浸入液体体积相同时,F与h不成正比;(b)60;0.50;(c)浸入相同体积,所受浮力不同;
③C。
12.【解答】解:(1)比较实验序号2~7数据,随着圆柱体下表面到水面距离h的增大,水对容器底部压力的增加量△F水在逐渐变大,说明在底面积不变时,当圆柱体浸入水中的深度越深,则水对容器底部的压力越大;
(2)分析实验序号2~7数据数据,圆柱体受到的浮力F浮的值都等于圆柱体下表面到水面的距离h的4倍,说明物体所受浮力的大小与物体浸入液体的深度成正比关系;
(3)比较实验序号8~9数据发现,△F水、F浮不再随h的变化而变化,说明物体已完全浸入水中,物体浸入水中的体积不再发生变化;
(4)容器上半部分的圆柱横截面积小于下半部分的,当物体开始进入水中,液体具有流动性,对容器内壁压力不同,平衡了物体所受的力,因此,分析实验序号5~9数据得出的结论与分析实验序号2~4数据得出的结论不符;
(5)根据实验数据,△F水呈现的两种不同变化关系与容器的形状有关,容器是由上、下两个横截面积不同的圆柱形构成的,实验中第2~4组数据,△F水的变化比率为0.2,实验第5~9组数据,△F水的变化比率为0.7,则上下面积之比为2:7。
故答案为:(1)随着圆柱体浸入水中深度越深,水对容器底部压力越大;(2)随着圆柱体浸入水中深度越深,圆柱体受到水的浮力越大;(3)圆柱体全部浸入水中;(4)容器上下横截面积不同;(5)2:7。
13.【解答】解:
(1)由图c可知,弹簧测力计下竖直挂着石块,是用测力计测量石块的重力;
(2)由图可知,图c测出了石块的重力,图d测出了石块浸没在液体中时测力计的拉力,图b测出空桶的重力,图e测出桶和石块排开液体的重力;
则物体浸入液体时受到的浮力为F2﹣F3,物体排开液体的重力为F4﹣F1,
如果F2﹣F3=F4﹣F1时,即物体浸在液体中受到的浮力等于物体排开液体的重力,阿基米德原理就成立。
(3)A.图(a)中溢杯内未盛满水,则测得排开水的重力会偏小,会影响验证结果。
B.图(b)中小桶内有少量水,石块排开水后,小桶重力的两次示数之差仍为排开水的重力,不影响实验结果。
C.图(d)中石块未浸没水中,此时浮力小,排开的水的体积也小,不影响实验结果。
故答案为:(1)弹簧测力计;重力;(2)F2﹣F3=F4﹣F1;(3)A。
14.【解答】解:(1)对溢水杯整体受力分析知,整体受竖直向下的重力、竖直向上的支持力、竖直向上的拉力,即G=F1+F2,
当G不再变化时,则溢水杯不再溢水,由表可知1、2、3次实验F1+F2的和都是28.5N,第4次F1+F2的和是28N,说明有水溢出,从第5s开始F1+F2的和都是27.5N,
综合分析从实验序号3开始,溢水杯内水面不再上升;在整个实验过程中,共溢出水28.5N﹣27.5N=1N;
(2)由表格数据知从1~4次实验,弹簧测力计的示数逐渐减小,说明合金块没有全部浸没,
5、6两次弹簧测力计的示数保持7.5N不变,说明合金块全部浸没了,
到第7次弹簧测力计的示数又减小了,说明合金块已经碰到容器底且容器底对物体有支持力了,故第7次的合金块下表面到溢水杯底部的距离h=0cm;
(3)①由3~6次实验数据可知,此时溢水杯内水的体积加上合金块排开水的体积刚好到溢水口,
根据物体间力的作用是相互的,合金块受到浮力等于合金块对水的压力,由阿基米德原理原理可知,合金块受到的浮力等于排开水的重力,
因此此时溢水杯中水的重力和合金块对水的压力之和等于仅在溢水杯中装水至溢水口时水的重力,
由题意可知,不计溢水杯的重力,所以此时台称的示数F2等于仅在溢水杯中装水至溢水口时水的重力,由表中3~6次实验数据可知,仅在溢水杯中装水至溢水口时水的重力为20.0N;
则溢水杯对水平面的压强:p====2000Pa,
因为轻质薄壁柱形容器对水平面的压强与液体对容器底部的压强相等,所以此时水对容器底部的压强:p水=p=2000Pa,由p=ρ水gh可得,溢水杯溢口到杯底的深度:h===0.2m;
②由5~6两次实验数据可知,合金块浸没时弹簧测力计的示数为7.5N,
由3~4两次实验数据可知,合金块每下降0.01m,弹簧测力计的示数减少0.5N,则合金块从第3次实验开始下降到刚好浸没时,弹簧测力计的示数减小了8.5N﹣7.5N=1N,此时合金块下降的距离为0.02m,因此合金块刚好浸没时,合金块下表明到溢水杯底的距离为0.10m,所以合金块的高度:h金=0.20m﹣0.10m=0.10m;
由3~4两次实验可知,合金块从第3次实验下降到第4次实验下降的高度:Δh=0.12m﹣0.11m=0.01m,增加的浮力:ΔF浮=8.5N﹣8.0N=0.5N,
由F浮=ρ液gV排可知,此时合金块排开水的体积增加量:ΔV排===5×10﹣5m3,
所以合金块的横截面积:S金===5×10﹣3m2,
所以合金块的体积:V金=S金h金=5×10﹣3m2×0.10m=5×10﹣4m3;
③合金块浸没在水中时V排=V金=5×10﹣4m3,此时合金块受到的浮力:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N,
第5、6两次实验中,合金块浸没在水中,此时合金块受到竖直向下的重力、竖直向上的浮力和拉力,
所以合金块的重力:G金=F浮+F1=5N+7.5N=12.5N,
合金块的质量:m金===1.25kg,
则合金块的密度:ρ金===2.5×103kg/m3。
故答案为:(1)3;1;(2)0;(3)2.5×103kg/m3。
15.【解答】解:①分析比较表中实验序号1~4的数据可知,随着圆柱体下降的深度越深,弹簧测力计的示数F1越来越小,台秤的示数F2越来越大,因此可得初步结论:圆柱体在浸入水的过程中,F1减小,F2增大。
②由表可以看出,在序号5、6两次实验中,弹簧测力计的示数F1不变、台秤的示数F2也不变,说明圆柱体受到的浮力不变,根据F浮=ρ液gV排可知,物体排开水的体积不变,则说明物体已全部浸没在水中。
③由表中的实验数据可得,任意两次实验中F1的减小量等于对应F2的增加量,在5、6两次实验中F1没有发生改变,F2也没有发生改变,因此可得出的结论是:圆柱体在水中缓慢下降的过程中,△F1=△F2。
取序号3、4两次实验,可得弹簧测力计F1的变化量为△F1=7.1N﹣6.8N=0.3N
则可得圆柱体在这两次实验中受到浮力的变化量为△F浮=△F1=0.3N
圆柱体的底面积为S,圆柱体下降的深度变化量为△h=4.0cm﹣3.0cm=1cm=0.01m
由阿基米德原理可得:
△F浮=ρ液g△V排=ρ液gS△h=1.0×103kg/m3×10N/kg×S×0.01m=0.3N,
解得:S=0.003m2;
由表格可知,当物体下降的深度为5cm时,物体已经完全浸没在水中,则有V排=V=Sh
圆柱体所受到的浮力为:
F浮=ρ液gV排=ρ液gSh=1.0×103kg/m3×10N/kg×0.003m2×0.05m=1.5N,
此时物体继续下降,但是受到的浮力不变,因此当圆柱体处于实验序号6的位置时,圆柱体受到的浮力为1.5N。
故答案为:①减小;增大;
②5、6;③△F1=△F2;1.5。
16.【解答】解:
①分析比较实验序号1与3(或5与6或7与9)的实验数据及相关条件知:圆柱体底面积相同,质量m不同,且质量越大,圆柱体底部到液面的深度h越大;故得出的结论是:圆柱体底面积相同,质量m越大,圆柱体底部到液面的深度h越大。
②分析比较实验序号2与3(或7与8)的实验数据及相关条件知,圆柱体质量m和体液密度ρ都相同,圆柱体的底面积S不同,且S越小,圆柱体底部到液面的深度h越大,故他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体质量m和体液密度ρ相同时,圆柱体的底面积S越小,圆柱体底部到液面的深度h越大。
③研究圆柱体的底部到液面的深度h与液体密度ρ的关系时,要控制圆柱体的质量和圆柱体的底面积相同
,只改变液体的密度,故分析比较2
与
4(或
3
与
8
或
6
与
9)实验序号的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体的质量m和底面积S相同,液体密度ρ越大,圆柱体的底部到液面的深度h越小。
④a、三个小组的同学对表格中的数据计算之后,进一步综合归纳结论,
a.实验2中有:=0.25
m;
实验5中有:=0.25m;
实验9中有:=0.25m;
2、5、9实验液面的深度h均为0.25m,
即圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相同,
同理,3与6或4与8圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值分别为0.3m和0.2m,
即圆柱体的底部到液面的深度h相同;
分析比较实验数据2、5与9或3与6或4与8可归纳得出的结论是:漂浮在液面上的圆柱体,圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相,圆柱体的底部到液面的深度h相同;
b、而2、5、9圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值0.25m,2、5、9实验液面的深度h均为0.25m;
3与6或4与8圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值分别为0.3m和0.2m,
而3与6或4与8实验液面的深度h分别为0.30m和0.20m,
因0.3m<0.25m<0.2m,
0.30m<0.25m<0.20m,
故得出的结论是:圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大,圆柱体的底部到液面的深度h越大;
⑤因圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大(小),圆柱体的底部到液面的深度h越大(小),故驳船载重小并且底部设计比较宽大,主要是为了减少驳船底部到液面的深度,避免搁浅的发生。
故答案为:
①圆柱体底面积相同,质量m越大,圆柱体底部到液面的深度h越大;
②圆柱体质量m和液体密度ρ相同时,圆柱体的底面积S越小,圆柱体底部到液面的深度h越大
③2
与
4(或
3
与
8
或
6
与
9);
④a.圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相同;
b.圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大,圆柱体的底部到液面的深度h越大
⑤驳船底部到液面的深度。
17.【解答】解:①根据1与2或3与4或5与6中的实验数据,可知放入物块的重力G不相同,竖直向下的压力F相同,由实验现象可知,G越大,V浸越大;由此可知,浮在水面上的物块,F相同,G越大,V浸越大;
②由实验结论:浮在水面上的物块,当物块所受重力G相同时,F越大,V浸越大。可知,观察序号1、3、5或2、4、6的实验现象并分析V浸和G、F的关系得出的;
(a)观察实验序号2与3的实验现象,可知:浮在水面上的物块,当V浸相同时,6N+3N=3N+6N
同理,4与5中的实验现象,当V浸相同时,6N+6N=3N+9N;
由此可知:浮在水面上的物块,当V浸相同时,G+F相同(G与F之和相同)。
(b)实验序号2与3中G+F=6N+3N=3N+6N=9N;
4与5中G+F=6N+6N=3N+9N=12N,
观察实验现象可知,4与5中比序号2与3中V浸大。
因此观察实验序号2与3和4与5中的实验现象,分析V浸和G、F的关系,
由此可得:浮在水面上的物块,G+F越大(G与F之和越大),V浸越大。
故答案为:①F相同,G越大,V浸越大;1、3、5或2、4、6;
②(a)G+F相同(G与F之和相同);(b)G+F越大(G与F之和越大),V浸越大。
18.【解答】解:①在实验的过程中,为了获得普遍的规律,应选用不同体积的物体进行探究,故应选多个物体进行实验;根据控制变量法可知,实验中应控制应控制浸入水中的体积相同;
②由表格中的1和4或2和5中的数据可知,物体的体积不同,浸入水中的体积相同,浮力相同,故F浮与V物无关;
根据序号1和2和3中的实验示意图及数据可知,同一个物体,浸入水中的体积越大,受到的浮力越大,即结论是:同一物体浸入水中,物体浸入水中的体积越大,受到的浮力越大;
③由图可知,上表面没有浸入水中,则上表面受到的水的压力F上=0;
下表面受到的压强为:p下=ρgh3;下表面受到的压力为:F下=p下S=ρgh3S;
则物体受到的浮力为:F浮=F下﹣F上=ρgh3S﹣0=ρgh3S。
故答案为:①多个;相同;②1和4或2和5;物体浸入水中的体积越大,受到的浮力越大;③F浮=F下﹣F上=ρgh3S﹣0=ρgh3S。
19.【解答】解:①分析比较表一或表二中ρ物、V露的数据及相关条件,可以看出,物体的密度越大,其浸入液体中的体积也越大,V露的就越越小;故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物越大时,V露越小。
②分析比较实验序号1、4或2、5或3、6中ρ物、V浸的数据及相关条件,可以看出,当物体的密度相同时,液体的密度越小,物体排开液体的体积越大,故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V浸越大,V露越小;
③进一步分析实验序号2和4中的数据及相关条件,可以看出,物体密度与液体密度的比值都是1:2,这时它们在液体中排开液体的体积是相同的。因此,得出的合理猜想是:漂浮在液面上体积相同的物块,当ρ物与ρ液的比值相同时,V浸是相同的:
第一组:ρ物=×1.5克/厘米3=0.3克/厘米3。
第一组:ρ物=×1克/厘米3=0.4克/厘米3。
故答案为:(1)当ρ物越大时,V露越小;②1、4或2、5或3、6;③0.3;0.4。
20.【解答】解:
(1)探究物体所受浮力的大小和物体排开液体体积的关系时,需要控制液体的密度和物体所在的深度一定,排开液体的体积不同,故需要对比的是图(a)、(b)、(c);
(2)选用的图(a)、(d)、(e)对比时,物体排开的液体的体积相同,液体的密度不同,所以探究的是物体所受浮力的大小和液体密度的关系;根据图可知,液体的密度不同,浮力不同,液体密度越大,受到的浮力越大,故可以得出结论:物体排开液体体积一定时,液体的密度越大,浮力越大;
(3)本实验采用了控制变量法。
故答案为:(1)(a)、(b)、(c);(2)浮力大小与液体密度的关系;物体排开液体体积一定时,液体的密度越大,浮力越大;(3)控制变量。
21.【解答】解:由题意,探究步骤(二):探究h与正方体物块的密度ρ物的关系
4、①你认为探究步骤(一)中需要改进的地方是:缺少记录实验数据的表格。
②“探究步骤(二):
探究h与正方体物块的密度ρ物的关系;
③由表中数据知:物块的密度越大,露出液面的高度越小;
④由表中数据知:物块的密度每增大200kg/m3,露出高度就减小2cm;
所以,可以推测:物块的密度增大到1000kg/m3时,露出水面的高度减小为零,
即:若露出水面的高度为零时,物块的密度ρ物与水的密度ρ水的比值等于1:1。
⑤正方体的体积为H3;
正方体液面下的长度为H﹣h,排开液体的体积为V排=H2(H﹣h),
根据阿基米德原理,正方体受到的浮力:
F=ρ液gV排=ρ液gH2(H﹣h),
根据漂浮的特点,F=G=ρ物gH3;
即ρ液gH2(H﹣h)=ρ物gH3
故关于正方体物块露出液面的高度h与它的边长H的比值:
=,故选C。
故答案为:探究h与正方体物块的密度ρ物的关系;
(4)①缺少记录实验数据的表格;
②正方体物块的密度ρ物;
③物块的密度越大,露出液面的高度越小;
④1:1;
⑤C。
22.【解答】解:
①分析比较实验序号2与3与4(或8与9与10)数据中△F和h的数据知,除1、7处,圆柱体下表面到液面的距离h增大为原来的几倍,F的变化量△F也增大为原来的几倍,故可得出的初步结论是:同一圆柱体浸入同种液体过程中,△F和h成正比;
②ρ1<ρ2,分析比较实验序号2与8(或3与9或4与10或5和11)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入不同液体过程中,h相同时,液体密度越大,△F越大;
③小明和小华继续分析表一、表二数据中F和h的关系,并进行相关思考。
(a)分析比较实验序号1~5(或7~11)数据中F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入同种液体过程中,F随h的增大而减小;
(b)分析比较实验序号5和6(或11和12)数据中F和h的关系及相关条件可知,当h≥H时,F不再随h的变化而变化,为验证该观点,他们换用高H为15厘米的圆柱体B继续实验,初步证明小明正确,据此表完成表三中的数据,如下所示:
实验序号
h(厘米)
F(牛)
13
15
20.0
14
17
20.0
15
20
20.0
故答案为:
①△F和h成正比;
②h相同时,液体密度越大,△F越大;
③(a)同一圆柱体浸入同种液体过程中,F随h的增大而减小;如上表所示。
23.【解答】解:
①分析比较表一中△F水和相关条件,可以看出三次放入容器中的物重G不同,但△F水的增加量均为1.0N,因此可得:△F水与G物无关;
②分析比较表二中实验序号4与5与6的数据可知,物体的体积越大,容器底部受到水的压力增加量△F水越大,且△F水与V物成正比,即:△F水与V物有关;
要得出△F水与V物无关,即:V物不同时,而容器底部受到液体压力的增加量△F水相同,由表二数据可知,实验5与7符合要求;
分析比较实验序号6与7与8的数据可知,物体的体积相同,但排开水的体积不相同,容器底部受到液体压力的增加量△F水不相同,因此可以得到:影响△F水的因素可能是排开液体的体积;
为了得到普遍规律,需要换用不同密度的液体多次实验。
故答案为:
①无关;
②△F水与V物成正比;5与7;排开液体的体积;不同密度的液体。
24.【解答】解:
①在该实验中,需要测量金属块在不同液体中排开的液体的体积,所以需要用到量筒;由图可知,金属块在空气中的重力示数为F1,由表格中的数据可知,金属块的重力为4N;
②a.根据实验序号1与2中ρ和F2数据及相关条件可知,金属块相同,浸没在不同的液体中,弹簧测力计两次示数的差值F1﹣F2为浮力的大小;液体的密度越小,弹簧测力计示数F2越大,则金属块所受的浮力F1﹣F2越小,所以实验结论为:对浸没在液体中的同一金属块而言,液体密度越小,弹簧测力计示数F2越大,金属块所受的浮力F1﹣F2越小;
b.分析比较实验序号1、2、3中ρ和F1﹣F2数据及相关条件可知:液体的密度ρ越小,弹簧测力计示数之差F1﹣F2与越小,且弹簧测力计示数之差F1﹣F2与ρ成正比;故结论为:对浸没在液体中的同一金属块而言,弹簧测力计示数之差F1﹣F2与ρ成正比;
③实验的过程中,测量的是弹簧测力计示数之差F1﹣F2即浮力的大小;实验中还测量了金属块排开液体的重力【即G排=ρg(V2﹣V1)】,所以探究的是浮力与物体排开液体的重力的关系,即探究的是阿基米德原理;故选A;
④为了得出普遍结论,应该换用换用不同材料的金属块多次实验,从而得到正确的结论。
故答案为:①量筒;4N;
②液体密度越小,弹簧测力计示数F2越大,金属块所受的浮力F1﹣F2越小;弹簧测力计示数之差F1﹣F2与ρ成正比;
③A;
④换用不同材料的金属块多次实验。
25.【解答】解:①由题可知,圆柱体的高为0.2米,当圆柱体下表面到液面的深度h=0.18米时,圆柱体上表面在液面上方,液体对圆柱体上表面的压力F1=0,
当圆柱体下表面到液面的深度h=0.20米时,圆柱体上表面刚好处于液面的位置,液体对圆柱体上表面的压力F1=0;
②分析比较实验序号1~5数据可以看出,当一圆柱体浸入同一液体中时,深度h越大,下表面所受的压力F2越大,故可得:当一圆柱体浸入同一液体中时,F2与h成正比;
③分析实验序号3与4与5数据可以看出,当一圆柱体浸没同一液体中时,虽然深度增加,但上、下表面受到的压力差却是相等的,故可得:当一圆柱体浸没同一液体中时,△F与h无关;
④圆柱体下表面在液体中的深度、液体的密度对圆柱体下表面受到液体的压力均有影响,故圆柱体下表面受到液体的压力大小与液体密度的关系,应控制圆柱体下表面在液体中的深度不变。
故答案为:①0;0;
②当一圆柱体浸入同一液体中时,F2与h成正比;
③当一圆柱体浸没同一液体中时,△F与h无关;
④圆柱体下表面在液体中的深度。
26.【解答】解:①由表中数据1与6或4与8可知,柱形物体浸入液体中,物体所受浮力相同,容器对桌面压力相同;
②分析表一、表二中实验序号5与8的数据,物体接触到了容器底,同时又受到了容器底的支持力,故与小林得出结论不符;
③分析实验序号1、2、3、4或6、7、8、9可知,同一柱形物体浸入同一柱形容器的液体中,F桌的变化量等于F浮的变化量;
④进一步分析实验序号1~5或76~10数据可得,同一物体浸入液体中,测力计示数F与容器对桌面的压力F桌之和是相同的,
故当测力计示数F为8N时,F桌的大小为90N﹣8N=82N。
故答案为:①1、6或4、8;②容器底对物体有向上的支持力;③同一柱形物体浸入同一柱形容器的液体中,F桌的变化量等于F浮的变化量;④82。
四.物体的浮沉条件及其应用(共4小题)
27.【解答】解:
①分析比较表一或表二中ρ物、V露的数据及相关条件,可以看出:当ρ液相同时(即用同种液体做实验),物体的密度越大,露出液面的体积V露越小;故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ液相同时,ρ物越大时,V露越小。
②要得出结论“漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V露越小”,根据控制变量法,应控制物体的密度相同,由表格数据可知,应分析比较实验序号1、4或2、5或3、6中ρ物、V浸的数据及相关条件;
③进一步分析实验序号2和4中的数据及相关条件,可以看出:虽然ρ物与ρ液均不同,但物体密度与液体密度的比值相同(都是1:2),这时V露是相同的(都是50.0厘米3)。
因此,得出的合理猜想是:漂浮在液面上体积相同的物块,当ρ物与ρ液的比值相同时,V露是相同的:
表三中,第一组:=,则ρ物=×1.5g/cm3=0.3g/cm3。
同理可得第二组:ρ物′=×1g/cm3=0.4g/cm3。
故答案为:
(1)当ρ液相同时,ρ物越大时,V露越小;(2)1、4或2、5或3、6;(3)0.3;0.4。
28.【解答】解:(1)∵空心铜球悬浮在水中:
V排=v=17.8cm3=17.8×10﹣6m3,
∴F浮=ρ水gV排
=1.0×103kg/m3×10N/kg×17.8×10﹣6m3
=0.178N;
∵小球悬浮时,浮力等于其重力,
∴G=F浮=0.178N。
答:(1)空心铜球的重力为0.178N;
(2)∵,
∴铜球的实心部分的体积:
=2×10﹣6m3=2cm3。
铜球中空心部分的体积:
V空=V﹣V实=17.8cm3﹣2cm3=15.8cm3。
答:铜球空心部分的体积15.8cm3。
29.【解答】解:
(1)受到的浮力为:F浮=ρ海水gV排=1×103kg/m3×10N/kg×24m3=2.4×105N;
(2)由阿基米德原理F浮=ρ海水gV排可知,物体在液体中所受的浮力大小只与液体的密度和排开液体的体积有关,与其它因素都无关。当抹香鲸继续下潜至2000米深的海底时,因为水密度不变,排开水的体积不变,所以受到的浮力不变。
答:(1)潜至此深度时,抹香鲸所受到的浮力大小F浮=2.4×105N。
(2)若抹香鲸继续下潜至2000米深的海底,它受到的浮力不变。原因是水密度不变,排开水的体积不变,根据F浮=ρ海水gV排可知其受到的浮力不变。
30.【解答】解:(1)G=mg=0.2kg×10N/kg=2N;
因为苹果漂浮
所以F浮=G=2N;
(2)由F浮=ρ液V排g可得,苹果排开水的体积:
V排===2×10﹣4m3;
(3)水降低的高度△h===2×10﹣2m;
容器底受到水的压强减少:
△p=ρg△h=1.0×103kg/m3×10N/kg×2×10﹣2m=200Pa。
答:(1)苹果受到的浮力大小为2牛。
(2)苹果排开水的体积为2×10﹣4m3。
(3)若将苹果缓慢从容器中取出(苹果带出的水忽略不计),则容器底受到水的压强减少了200Pa。
TOC
\o
"1-1"
\h
\u
一.阿基米德原理的应用(共4小题)
1
二.浮力大小的计算(共2小题)
3
三.探究影响浮力大小因素的实验(共20小题)
4
四.物体的浮沉条件及其应用(共4小题)
24
参考答案
27
一.阿基米德原理的应用(共4小题)
27
二.浮力大小的计算(共2小题)
29
三.探究影响浮力大小因素的实验(共20小题)
30
四.物体的浮沉条件及其应用(共4小题)
43
一.阿基米德原理的应用(共4小题)
1.某小组同学想探究漂浮在液面上的实心物体露出液面的体积V露与什么因素有关。他们选用了若干不同的实心圆柱体漂浮在不同液体中进行实验,并将物体的密度ρ物,物体的体积V物、液体的密度ρ液,以及物体露出液面的体积V露记录在表中。
实验序号
ρ物(×103千克/米3)
V物(×10﹣6/米3)
ρ液(×103千克/米3)
V露(×10﹣6米3)
1
0.4
10
1.0
6
2
0.4
15
1.0
9
3
0.4
20
1.0
12
4
0.6
15
0.9
5
5
0.6
15
1.2
7.5
6
0.8
15
1.0
3
7
0.8
15
1.5
7
8
0.8
24
1.2
﹣﹣
①分析比较实验序号1与2与3的数据中V露随V物的变化关系及相关条件,可得出:漂浮在液面上的实心物体,当ρ液和ρ物相同时,
。
②分析比较实验序号
的数据中V露随ρ液的变化关系及相关条件,可得出的初步结论是:漂浮在不同液体中的实心物体,当ρ物和V物相同时,V露随ρ液的增大而增大。
③根据实验序号
的数据可以研究V露随ρ物的变化关系。
④实验小组同学又进一步分析了表中1~7的实验数据,发现漂浮在液面上的实心物块,V露与ρ物、V物、ρ液存在一定的定量关系,由此他们推断表中空缺的数据应该是
。
2.在“验证阿基米德原理”的实验中,某小组同学用测力计悬挂着体积均为200厘米3的不同物体逐渐浸入到不同液体中,实验过程如图所示,他们观察并记录了测力计的示数及量筒中液体体积的变化,所有数据均记录在下表中。
液体密度(克/厘米3)
实验序号
测力计示数F1(牛)
测力计示数F2(牛)
F1﹣F2(牛)
液体体积V1(厘米3)
液体体积V2(厘米3)
V2﹣V1(厘米3)
1.0
1
5
4.5
0.5
100
150
50
2
5
4
1.0
100
200
100
3
5
3
2.0
100
300
200
4
5
0
5
100
300
200
1.2
5
1.8
1.2
0.6
125
175
50
6
1.8
0.6
1.2
125
225
100
7
1.8
0
1.8
125
275
150
①在此实验中量筒中液面的两次示数差(V2﹣V1)表示了
。
②分析比较实验序号1与2与3(或5与6与7)可初步得出的结论:
。
③分析比较实验序号
可初步得出的结论:当排开液体的体积相同时,液体密度越大,浸在液体中的物体受到的浮力越大。
④分析实验序号4中的数据及相关条件,产生这种现象的原因可能是
。
3.如图所示,重为19.6牛的物块A静止在水中,此时弹簧测力计的示数为4.9牛。
①求物块A受到的浮力F浮。
②求物块A的体积V物。
4.小明同学想利用一组氮气球来提升货物(如图所示),已知他所用的轻质薄壁气球的总体积为10米3,其内部所充入的氦气密度都为0.18千克/米3
(1)求这组气球内的氮气质量m氮。
(2)求这组气球在空气中所受的浮力大小F浮(空气密度为1.29千克/米3)
(3)若忽略货物在空气中所受的浮力,求该组气球所能提升货物的最大重力Gm最大。
二.浮力大小的计算(共2小题)
5.某实心长方体在空气中称重弹簧测力计示数为24.5N,把它浸没在水中弹簧测力计示数为14.7N.求:
(1)该物体受到浮力。
(2)如该长方体的上下两表面和水面平行,它上表面受到压力为10N,求下表面所受压力。
(3)长方体的密度。
6.水平桌面上放置一轻质圆筒,筒内装有0.2米深的某液体,如图(a)所示。弹簧测力计悬挂底面积为10﹣2米2、高为0.1米的圆柱体,从液面逐渐浸入直到浸没,弹簧测力计示数F与圆柱体浸入液体深度h的关系如(b)所示。圆筒的厚度忽略不计,筒内液体没有溢出,圆柱体不碰到筒底。
①若F1=9.8牛,F2=1.96牛,求圆柱体浸没时所受浮力F浮;筒内液体的密度ρ液。
②圆柱体未浸入时筒底受到的液体压强p液。
③若轻质圆筒的底面积为2S,筒内液体深度为2h,液体密度为ρ,圆柱体底面积为S、高为h,求圆柱体浸没时,圆筒对桌面的压强p桌.(用字母表示)
三.探究影响浮力大小因素的实验(共20小题)
7.为了探究柱体A逐渐浸入柱形容器内的水中时(水没有溢出),弹簧测力计示数F的变化情况。现有底面积为100厘米2的薄壁柱形容器,容器内装有深度为20厘米的水,放在水平桌面上,实心柱体A高H为20厘米。如图所示,小明将柱体A通过细线挂在弹簧测力计下,从柱体A接触水面开始,将液面到柱体下表面的距离h、相应的弹簧测力计示数F、物体重力G与F的差值△F记录在表一中,(不计细线的重力)
表一
实验序号
1
2
3
4
5
6
7
8
h(cm)
0
2
4
6
8
10
12
14
F(N)
8
7
6
5
4
3
2
1
△F(N)
0
1
2
3
4
5
6
7
①分析比较实验序号1﹣8中F与h的变化关系及相关条件可得:同一柱体逐渐浸入柱形容器内的水中,当h小于H时,
。
②分析比较实验序号1﹣8中△F与h的变化关系及相关条件可得:同一柱体逐渐浸入柱形容器内的水中,
。
③柱体A的重力为
牛,实验序号6的实验时,A下表面所受液体压力为
牛。
④小红同学想在小明实验的基础上继续进行实验,她预设的数据如表二所示,小明看了以后认为这两次实验无法进行。
表二
实验序号
9
10
h(cm)
18
20
F(N)
﹣
﹣
△F(N)
﹣
﹣
你认为小明的观点是
的(选填“正确”或“错误”),理由是
。
8.为探究浸没在水中的物体对容器底的压力与哪些因素有关,某小组同学利用DIS数据采集系统及若干重力G和密度ρ已知的实心物体等器材进行实验。他们将实心物体放入盛水的平底容器中(如图所示),测出物体对容器底的压力F,并将实验数据记录在表一中。
表
一
实验序号
1
2
3
4
5
6
7
8
9
密度ρ(g/cm3)
2.0
2.5
3.0
重力G
(N)
4
8
12
4
8
12
3
6
9
压力F
(N)
2.0
4.0
6.0
2.4
4.8
7.2
2.0
4.0
6.0
表二
(ρ﹣ρ水):ρ
1:2
3:5
2:3
F:G
(1)分析表一中实验序号
中的数据及相关条件可初步得出:当物体的重力相同时,浸没在水中的物体对容器底的压力随物体密度的增大而增大。
(2)分析表一中实验序号1、2、3(或4、5、6,或7、8、9)中的数据及相关条件可初步得出:
。
(3)小组同学进一步综合分析表一中的数据有了新发现,他们将经计算得到的部分数据记录在表二中。
(a)表二中空缺的数据依次为
、
、
。
(b)按表二中数据反映的规律推理:若浸没在水中某实心物体的密度ρ=4g/cm3,重力G=12N,则物体对容器底的压力F=
N。
9.为了研究物体漂浮在水面上时的特点,某小组同学用甲、乙两种材料制成体积不同的若干块物块进行实验,甲材料的密度为ρ甲,乙材料的密度ρ乙,且ρ甲<ρ乙.如图所示,他们让物块漂浮在水面上,测量并记录了物块的总体积和露出水面的体积,并将实验数据记录在下表中。
材料
实验
物块体积
露出水面体积
材料
实验
物块体积
露出水面体积
序号
(10﹣6米3)
(10﹣6米3)
序号
(10﹣6米3)
(10﹣6米3)
甲
1
10
6
乙
6
8
1.6
2
20
12
7
10
2
3
30
18
8
30
6
4
40
24
9
35
7
5
50
30
10
45
9
①分析比较实验序号
数据,可得出的初步结论是:同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比。
②分析比较实验序号1与7、3与8的数据,可得出的初步结论是:
。
③他们分别分析了“露出水面的体积”和“物体体积”的比例关系,可以得出的进一步结论是:
(a)
。
(b)
。
10.为研究物体在液体中受到向上的力与哪些因素有关,小明设计了方案进行实验。小明用弹簧测力计将一圆柱体悬挂在空容器中,如图所示,此时弹簧测力计的示数为F0,然后逐次向容器中注入液体A,并将圆柱体下表面到液面的距离h、相应的弹簧测力计示数F、F0与F的差值△F记录在表一中。为进一步探究,小明换用液体B重复实验,并将数据记录在表二中。(液体A、B密度分别为ρA、ρB,且ρA>ρB)
表一(液体A)
表二(液体B)
实验序号
h(厘米)
F(牛)
△F(牛)
实验序号
h(厘米)
F(牛)
△F(牛)
1
3.0
8.5
1.5
5
3.0
8.8
1.2
2
6.0
7.0
3.0
6
6.0
7.6
2.4
3
9.0
5.5
4.5
7
9.0
6.4
3.6
4
12.0
5.0
5.0
8
12.0
6.0
4.0
①分析比较实验序号1、2与3(或5、6与7)数据中F和h的关系及相关条件,可得初步结论:
同一物体在同一种液体中,
。
②分析比较实验序号1、2与3(或5、6与7)数据中△F和h的关系及相关条件,可得初步结论:
同一物体在同一种液体中,
。
③分析比较实验序号1、5(或2、6,或3、7)数据中△F和h的关系及相关条件,可得初步结论是:
同一物体在
。
④实验中圆柱体重力为
牛,高度为
厘米。
11.小徐和小汇在学习“浮力”时,根据生活经验,对物体受到浮力的大小与哪些因素有关提出猜想并进行了研究。
①根据鸡蛋在水中沉底、在盐水中漂浮的现象,他们猜想浮力的大小可能与
有关。根据游泳时的感觉,他们猜想浮力的大小可能与物体浸入液体的深度,以及物体浸入液体的体积有关。
②为了验证猜想,他们用压力传感器将一长方体金属块悬挂在空量筒中,如图所示,然后逐次向容器中注入液体A,测出金属块下表面到液面的距离即金属块浸入液体的深度h,计算出金属块浸入液体的体积V和金属块受到的浮力F,把实验数据记录在表一中。为了进一步探究,他们还换用了液体B重复实验,并把实验数据记录在表二中。(液体A、B密度分别为ρA、ρB,ρA>ρB)
表一:将金属块浸入液体A中
实验序号
浸入的深度h(厘米)
浸入的体积V(厘米3)
浮力F(牛)
1
2.0
12
0.12
2
6.0
36
0.36
3
10.0
60
0.60
4
15.0
60
0.60
表二:将金属块浸入液体B中
实验序号
浸入的深度h(厘米)
浸入的体积V(厘米3)
浮力F(牛)
5
2.0
12
0.10
6
6.0
36
0.30
7
10.0
60
0.50
8
15.0
(a)小汇分析比较实验序号1、2、3的F和V、h的数据后,得出初步结论:同一物体浸入同一液体中,F与V成正比,而且F与h成正比。
小徐分析比较实验序号
的数据,认为小汇的结论存在问题,请写出小徐观点的依据
。
(b)请补全实验序号8中的数据。
、
。
(c)他们分析比较表一和表二中的数据,得出结论:同一物体浸入不同液体中:
。
③他们交流后,认为上述得出的结论还不够完善,需要增加一次实验进行论证,下列方案中你建议采用方案
。
A.仍用上述金属块,浸入密度不同的液体C中,重复实验
B.仍用上述金属块,增加金属块浸入液体A或B中的深度进行实验
C.换用其他物质(如其他材质的金属块),仍在液体A或B中进行实验
12.某小组同学研究当圆柱体浸入水中时,容器底部受到水压力的增加量和圆柱体所受浮力大小的变化情况。实验选用由上、下两个横截面积不同的圆柱形构成的容器,如图所示。实验时将重为8.0牛的圆柱体缓慢浸入水中,将圆柱体下表面到水面的距离h、弹簧测力计的示数F1、容器底部受到水的压力F2记录在如表中,并计算出相应的浮力F浮和水对容器底部压力的增加量△F水。
实验序号
h(厘米)
F1(牛)
F2(牛)
F浮(牛)
△F水(牛)
1
0
8.0
12.0
0
0
2
0.5
7.8
12.2
0.2
0.2
3
1.0
7.6
12.4
0.4
0.4
4
1.5
7.4
12.6
0.6
0.6
5
2.0
7.2
13.0
0.8
1.0
6
2.5
7.0
13.7
1.0
1.7
7
3.0
6.8
14.4
1.2
2.4
8
3.5
6.6
15.1
1.4
3.1
9
4.0
6.6
15.1
1.4
3.1
①分析比较实验序号2~7数据中△F水与h的变化关系,可得出的初步结论是:在圆柱体浸入水的过程中,
;
②分析比较实验序号2~7数据中F浮与h的变化关系,可得出的初步结论是:在圆柱体浸入水的过程中,
;
③分析比较实验序号8和9数据发现,△F水、F浮不再随h的变化而变化,其原因是
;
④该组同学分析实验序号2~4数据可得出的结论是:在圆柱体浸入水的过程中,△F水与F浮大小相等。但实验序号5~9数据与上述结论不符,其原因是
;
⑤请根据实验数据推断:组成容器的上、下两部分圆柱形的横截面积之比为
。
13.小华做“验证阿基米德原理”的实验中,用图(a)所示的溢杯和小桶收集石块排开的水,他的实验过程分别如图(b)、(c)、(d)、(e)所示。
(1)图(c)所示,是小华在使用
测量石块的
。
(2)若图中四个测量值F1、F2、F3、F4满足关系式
,该原理将得到验证。
(3)以下关于实验过程中的操作,会影响验证结果的是
。
A.图(a)中溢杯内未盛满水。
B.图(b)中小桶内有少量水。
C.图(d)中石块未浸没水中。
14.某兴趣小组在学习浮力时,将一底面积为0.01米2的轻质柱形溢水杯放置于台秤上,并在溢水杯内装入适量水。然后,用测力计悬挂一柱形合金块慢慢浸入水中,实验过程如图所示。他们记录了合金块下表面到溢水杯底部的距离h、测力计示数F1、台秤示数F2,实验数据如表所示。请根据表格中相关信息,回答下列问题。(本题g取10牛/千克)
实验序号
1
2
3
4
5
6
7
h
(米)
0.15
0.14
0.12
0.11
0.09
0.08
F1(牛)
11.5
10.5
8.5
8.0
7.5
7.5
6.5
F2
(牛)
17.0
18.0
20.0
20.0
20.0
20.0
21.0
(1)从实验序号
开始,溢水杯内水面不再上升;在整个实验过程中,共溢出水
牛。
(2)请完成序号7空缺数的填写。
(3)该合金块的密度是
千克/米3。
15.某小组同学用如图所示装置,研究圆柱体在水中下降的过程中弹簧测力计示数和台秤示数的变化情况。他们使圆柱体在水中缓慢下降,将圆柱体下表面到水面的距离h、弹簧测力计的示数F1、台秤的示数F2记录在下表中。
实验序号
h(厘米)
F1(牛)
F2(牛)
1
1.0
7.7
10.3
2
2.0
7.4
10.6
3
3.0
7.1
10.9
4
4.0
6.8
11.2
5
5.0
6.5
11.5
6
6.0
6.5
11.5
①分析比较实验序号1~4的数据中F1、F2的变化情况及相关条件,可得出的初步结论是:圆柱体在浸入水的过程中,F1
,F2
;
②表中实验序号
的数据表明,圆柱体在相应的位置已全部浸没在水中;
③表中两组数据间F1变化量的大小为△F1,相应的F2变化量的大小为△F2,分析比较实验序号1~6的数据,可得出的结论是:圆柱体在水中缓慢下降的过程中,△F1与△F2的关系是
。当圆柱体处于实验序号6的位置时,所受浮力的大小为
牛。
16.甲、乙、丙三个小组同学发现如图(a)所示的驳船底部设计得比较宽大。于是,他们想“探究驳船的底部到液面的深度与哪些因素有关”。实验时,他们用圆柱体来模拟驳船,并选取了密度不同的三种液体来模拟不同密度的水域,将质量和底面积大小不同的圆柱体分别放入液体中,每次都使圆柱体漂浮在液面上,如图(b)所示。实验过程中,他们测量了所用圆柱体的质量m、底面积S和它的底部到液面的深度h,所有数据均记录在下表中。
序号
小组
容器中液体的密度ρ(×103千克/米3)
圆柱体的质量m
(千克)
圆柱体的底面积S(10﹣2米2)
深度h(米)
1
甲
0.8
0.06
0.05
0.15
2
0.8
0.12
0.06
0.25
3
0.8
0.12
0.05
0.30
4
乙
1.0
0.12
0.06
0.20
5
1.0
0.25
0.10
0.25
6
1.0
0.30
0.10
0.30
7
丙
1.2
0.12
0.10
0.10
8
1.2
0.12
0.05
0.20
9
1.2
0.30
0.10
0.25
①分析比较实验序号1与3(或5与6或7与9)的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体底面积S和液体密度ρ相同时,
。
②分析比较实验序号2与3(或7与8)的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,
。
③分析比较实验序号
的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体的质量m和底面积S相同,液体密度ρ越大,圆柱体的底部到液面的深度h越小。
④三个小组的同学对表格中的数据计算之后,进一步综合归纳结论,
a.分析比较实验数据2、5与9或3与6或4与8可归纳得出的结论是:漂浮在液面上的圆柱体,
,圆柱体的底部到液面的深度h相同。
b.分析比较实验数据2、5与9和3与6和4与8可归纳得出的结论是:漂浮在液面上的圆柱体,
。
⑤通过上述研究的过程,同学们明白了驳船载重小并且底部设计比较宽大,主要是为了减少
,避免搁浅的发生。
17.小明将六个体积相同、重力G不同的正方体物块放入水中(ρ物<ρ水),研究浮在水中的物块浸入水中的体积V浸的情况。实验时,他将物块放入同一个盛有水的大容器中,然后对物块施加竖直向下的压力F,待物块静止后,观察物块浸入水中的体积V浸.相关实验数据和现象如下表所示。
实验序号
1
2
3
4
5
6
放入物块的重力G(牛)
3
6
3
6
3
6
竖直向下的压力F(牛)
3
3
6
6
9
9
实验现象
①观察序号1与2或3与4或5与6中的实验现象并分析V浸和G、F的关系,可初步归纳得出的结论是:浮在水面上的物块,
。观察序号
的实验现象并分析V浸和G、F的关系,可得出的初步结论是:浮在水面上的物块,当物块所受重力G相同时,F越大,V浸越大。
②综合分析表中的实验现象及相关数据,进一步归纳结论。
(a)观察实验序号2与3或4与5中的实验现象并分析V浸和G、F的关系,可得出:浮在水面上的物块,
,V浸相同。
(b)观察实验序号2与3和4与5中的实验现象并分析V浸和G、F的关系,可得出:浮在水面上的物块,
。
18.为了探究物体受到的浮力F浮与物体体积V物有关还是与物体浸入液体的体积V浸有关,某小组同学设计方案进行探究。
物体
A
B
C
体积
4V
2V
V
①现有可供选择的物体如下表所示,在研究F浮与V物的关系时应选择
物体(选题“一个”或“多个”),并控制其浸入水中的体积
(选填“相同”或“不同”),测出其受到的浮力。
②该小组同学经过讨论完善方案后继续实验,将体积不同的物体浸入水中,测出物体受到的浮力,实验现象和数据如下表所示。
实验序号
1
2
3
4
5
实验示意图
V物(米3)
0.4×10﹣3
0.2×10﹣3
V浸(米3)
0.1×10﹣3
0.2×10﹣3
0.4×10﹣3
0.1×10﹣3
0.2×10﹣3
F浮(牛)
1
2
4
1
2
根据序号
的实验示意图及数据,可得F浮与V物无关。
根据序号1和2和3中的实验示意图及是数据,可得出的初步结论是:同一物体浸入水中,
。
③他们尝试利用液体内部压强知识阐述浮力产生的原因,当物体浸没在液体中时,如图1所示:
F浮=F2﹣F1=p2S﹣p1S=p液gh2S﹣p液gh1S=p液g(h2﹣h1)S=p液gV物
当物体部分浸入液体中时,如图2所示,请利用液体内部压强知识推导出物体受到的浮力。
。
19.为了探究漂浮在液面上的物块露出液面的体积V露与物块密度ρ物、液体密度ρ液的关系,某小组同学选取体积V物相同、ρ物不同的物块进行实验,测出其漂浮在水和酒精液面上时露出液面的体积V露,相关数据记录在表一、表二中。
表一:水
ρ液(克/厘米3)
实验序号
ρ物(克/厘米3)
V浸(厘米3)
1.0
1
0.4
40
2
0.5
50
3
0.6
60
表二:酒精
ρ液(克/厘米3)
实验序号
ρ物(克/厘米3)
V浸(厘米3)
0.8
4
0.4
50
5
0.5
62.5
6
0.6
75
表三
第一组
ρ液=1.0克/厘米3ρ物=0.2克/厘米3
ρ液=1.5克/厘米3ρ物=
克/厘米3
第二组
ρ液=1.0克/厘米3ρ物=
克/厘米3
ρ液=1.5克/厘米3ρ物=0.6克/厘米3
①分析比较表一或表二中ρ物、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上的物块,
。
②分析比较实验序号
中,ρ液、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上的物块,当V物、ρ物相同时,ρ液越小,V露越小。
③由实验序号2与4的数据及相关条件,发现漂浮在液面上V物相同的物块,存在与ρ液均不同而V露相同的现象。若用V物相同的物块进一步实验,请在表三中填入拟进行实验的数据,使每一组实验均能研究上述现象。
20.在探究“影响浮力大小的因素”这一问题时,请你根据图中实验操作,从中选出一些图,针对某一个因素进行探究,并通过分析弹簧测力计的示数,说明你的探究结果。
(1)探究的因素是:浮力大小与物体排开液体体积;选用的图是:
(填图中序号);探究的结果是:物体排开液体体积越大,浮力越大。
(2)探究的因素是:
;选用的图是:(a)、(d)、(e);探究的结果是:
。
(3)上述所设计的方案,采用的科学方法是
法。
21.为了探究漂浮在液面上的均匀实心正方体物块露出液面的高度h与哪些因素有关,某小组同学进行了讨论并形成了两个猜想,猜想(一)认为h的大小可能与液体的密度有关猜想(二)认为h的大小可能与正方体物块的密度ρ物有关。为此,他们与老师一起设计了探究方案如下:
探究步骤(一):探究h与液体密度ρ液的关系
1.测出正方体物块的边长H。
2.将这个正方体物块分别漂浮于不同液体中,测出相应的h值。
3.记录数据并归纳总结结论。
探究步骤(二):探究h与
的关系
1.选用不同密度的若干正方体物块,要求它们的边长相等,测出边长H。
2.将不同密度的正方体物块分别漂浮于水面上,测出相应的h值。
3.设计记录数据表如表一所示:
表一
实验序号
物块的密度ρ物(千克/立方米)
水的密度ρ液(千克/立方米)
h(厘米)
H(厘米)
1
2
3
…
…
…
…
…
4.记录数据并归纳总结结论。
探究步骤(三):进一步综合分析并归纳总结结论。
①你认为探究步骤(一)中需要改进的地方是什么?答:
。
②请你填写完整“探究步骤(二):探究h与
的关系”。
③该小组同学在完善方案后进行了实验探究活动,其中实验步骤(二)收集到的数据如表二所示;
表二
实验序号
物块的密度(千克/立方米)
水的密度(千克/立方米)
h(厘米)
H(厘米)
1
400
1000
6
10
2
600
1000
4
10
3
800
1000
2
10
…
…
…
…
…
根据实验序号1与2与3,初步分析可得出的结论是:漂浮在水面上的物块,
。
④根据表二的数据可以推测:若露出水面的高度为零时,物块的密度ρ物与水的密度ρ水的比值等于
。
⑤关于正方体物块露出液面的高度h与它的边长H的比值,正确的是
。
A.
B.
C.
D.
22.小明和小华两位同学通过实验研究圆柱体浸入液体(足够深)的过程中测力计示数F的变化情况。如图所示,他们将高H为10厘米的圆柱体A挂在测力计下,逐步改变其下表面到液面的距离h,读出相应的测力计示数F,将h、F、及每一次实验中F的变化量△F记录在表一中。然后,他们变换液体重复实验,将数据记录在表二中。(已知ρ1<ρ2)
表一(液体密度为ρ1)
实验序号
h(厘米)
F(牛)
△F(牛)
1
0
22.0
0
2
1
21.2
0.8
3
4
18.8
3.2
4
8
15.6
6.4
5
10
14.0
8.0
6
14
14.0
8.0
表二(液体密度为ρ2)
实验序号
h(厘米)
F(牛)
△F(牛)
7
0
22.0
0
8
1
21.0
1.0
9
4
18.0
4.0
10
8
14.0
8.0
11
10
12.0
10.0
12
14
12.0
10.0
①分析比较实验序号2与3与4(或8与9与10)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入同种液体过程中,
。
②分析比较实验序号2与8(或3与9或4与10或5和11)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入不同液体过程中,
。
③小明和小华继续分析表一、表二数据中F和h的关系,并进行相关思考。
(a)分析比较实验序号1~5(或7~11)数据中F和h的关系及相关条件,可得出的初步结论是:
。
(b)分析比较实验序号5和6(或11和12)数据中F和h的关系及相关条件,小明认为:“当h满足一定条件时,F不再随h的变化而变化。”为验证该观点,他们换用高H为15厘米的圆柱体B继续实验,初步证明小明正确。表三记录了他们的部分实验数据,请将表三中的数据填写完整。
表三(液体密度为ρ1)
实验序号
h(厘米)
F(牛)
13
15
14
17
20.0
15
20
23.某小组同学通过实验探究盛有液体的容器在放入物体前、后容器底部受到液体压力的增加量△F液与哪些因素有关。
①他们猜想:△F液与放入物体的重力G物有关,于是选用重力不同而体积相同的物体和水进行实验。他们将物体先后放入同一盛有水的容器中,并测得容器底部受到水的压力增加量△F水.实验示意图及相应数据见表一。
表一
实验序号
1
2
3
实验示意图
G物(牛)
2.0
2.4
2.8
△F水(牛)
1.0
1.0
1.0
分析比较表一中△F水和相关条件,可得:△F水与G物
(选填“有关”或“无关”)。
②他们提出新的猜想:△F水与放入物体的体积V物有关,于是选择不同物体先后放入盛有相等质量水的相同容器中,待物体静止,测得△F水.实验示意图及相应数据见表二。
表二
实验序号
4
5
6
7
8
现象
V物(×10﹣4米3)
0
0.9
1.2
1.4
1.4
1.4
△F水(牛)
0
0.9
1.2
1.4
1.2
1.0
他们首先分析比较了实验序号4与5与6,得到:△F水与V物有关,且
。接着,他们全面分析后,比较了实验序号
,发现:△F水与V物无关。他们交流讨论后,分析比较了实验序号6与7与8,得到:影响△F水的因素可能是
,继续研究,还应选用
完成实验。
24.小同学选用弹簧测力计、
和系细绳的金属块各一个,及三种密度不同液体进行如图所示实验,设计的实验表格如下。小李同学将测得数据及根据数据计算得到的结果记录在表中(部分未显示)。
实验序号
ρ(×103千克/米3)
V1(×10﹣3米3)
V2(×10﹣3米3)
F1(牛)
F2(牛)
F1﹣F2(牛)
ρg(V2﹣V1)
1
1.2
4.0
2.8
1.2
2
1.0
4.0
3.0
1.0
3
0.8
4.0
3.2
0.8
①填写
所对应的器材,该金属块所受重力为
。
②分析实验数据并得出初步结论:
a.分析比较实验序号1与2中ρ和F2数据及相关条件可初步得出结论,对浸没在液体中的同一金属块而言,
。
b.分析比较实验序号1、2、3中ρ和F1﹣F2数据及相关条件可初步得出结论,对浸没在液体中的同一金属块而言,
。
③根据小李同学所设计的表格和实验步骤,该实验的实验目的应该是
(填写选项序号“A”“B”“C”或“D”)。
A.验证阿基米德原理
B.探究物体所受浮力与哪些因素有关
C.探究物体所受浮力与体积的关系
D.练习使用弹簧测力计测物体所受浮力
④为使实验结论更有普遍性,请提出补充设计建议
。
25.小明同学研究圆柱体在某种液体中下降的过程中,圆柱体上、下表面受到液体的压力大小F1和F2与圆柱体下表面浸没在液体中深度h的关系,如图所示。小明使高为0.2米的实心圆柱体在液体中缓慢下降,测量出圆柱体下表面到液面的深度h、利用仪器测出圆柱体上、下表面处液体的压强,利用公式求得圆柱体上、下表面受到液体的压力F1和F2,进一步计算圆柱体下表面与上表面受到液体的压力差△F,记录在下表中。
实验序号
h(米)
F1(牛)
F2(牛)
△F(牛)
1
0.18
a
18.0
2
0.20
b
20.0
3
0.22
2.0
22.0
20.0
4
0.24
4.0
24.0
20.0
5
0.26
6.0
26.0
20.0
①a、b分别为
和
。
②分析比较实验序号1~5数据中,F2与h的关系及相关条件,可得出的初步结论是:
。
③分析比较实验序号3与4与5数据中,△F与h关系及相关条件,可得出的初步结论是:
。
④如果进一步研究圆柱体浸没在液体中,圆柱体下表面受到液体的压力大小与液体密度的关系。实验方案中应该控制不变的物理量为:
(选填“圆柱体下表面在液体中的深度”或“液体密度”)
26.小林和小徐通过实验研究将物体浸入液体的过程中,容器对水平桌面压力的变化情况。如图18所示,他们将重力分别为30牛、40牛的甲、乙两个柱形物体,先后挂在弹簧测力计下,并将其逐渐浸入放在水平桌面上的同一柱形容器的液体中(液体不溢出)。他们读出测力计示数F,并测得容器对桌面的压力F桌,并根据相关物理量计算出物体所受浮力F浮,将数据记录在表一、表二中。
实验序号
F(N)
F浮(N)
F桌(N)
1
20
10
60
2
16
14
64
3
12
18
68
4
8
22
72
5
4
22
76
表二
物体乙的重为40N
实验序号
F(N)
F浮(N)
F桌(N)
6
30
10
60
7
25
15
65
8
18
22
72
9
10
30
80
10
8
30
①小林分析比较实验序号
后得出结论:不同柱形物体浸入同一柱形容器液体中时,物体所受浮力相同,容器对桌面压力相同。
②分析表一、表二中实验序号5与8的数据与小林得出结论不符的原因
。
③小徐分析比较实验序号1、2、3、4(或6、7、8、9)F桌变化量与F浮变化量的关系后得出初步结论:
。
④进一步分析表一和表二的数据,可得实验序号10的F桌的大小为
牛。
四.物体的浮沉条件及其应用(共4小题)
27.为了探究漂浮在液面上的物块露出液面的体积V露与物块密度ρ物、液体密度ρ液的关系,某小组同学选取体积相同、ρ物不同的物块进行实验,测出其漂浮在水和酒精液面上时露出液面的体积V露,相关数据记录在表一、表二中。
表一:水
实验序号
ρ液(克/厘米3)
ρ物(克/厘米3)
V露(厘米3)
1
1.0
0.4
60.0
2
0.5
50.0
3
0.6
40.0
表二:酒精
实验序号
ρ液(克/厘米3)
ρ物(克/厘米3)
V露(厘米3)
4
0.8
0.4
50.0
5
0.5
37.5
6
0.6
25.0
(1)分析比较表一或表二中ρ物、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上体积相同的物块,
。
(2)分析比较实验序号
中ρ液、V露的数据及相关条件,可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V露越小。
(3)由实验序号2与4的数据及相关条件,发现漂浮在液面上体积相同的物块,存在ρ物与ρ液均不同而V露相同的现象。若用其它体积相同的物块进一步实验,请在表三中填入拟进行实验的数据,使每一组实验均能研究上述现象。
表三:密度值(克/厘米)
第一组
ρ液=1.0ρ物=0.2
ρ液=1.5ρ物=
第三组
ρ液=1.0ρ物=
ρ液=1.5ρ物=0.6
28.把一个外观体积为17.8cm3的空心铜球放入水中,它恰好处于悬浮状态。已知铜的密度是8.9×103kg/m3,g取10N/kg,求:
(1)空心铜球的重力;
(2)铜球空心部分的体积。
29.抹香鲸是世界上最大的齿鲸,它在所有鲸中潜水最深且最久,号称“潜水冠军”,如图所示。一头体长19米,体积24米3的成年抹香鲸可轻松潜至1000米深的海底。
(1)求潜至此深度时,抹香鲸所受到的浮力大小F浮。
(2)若抹香鲸继续下潜至2000米深的海底,它受到的浮力会变化吗?为什么?
(假设海水密度为1×103千克/米3,且不随深度变化)
30.如图所示,装水的圆柱形玻璃容器汇总漂浮着质量为0.2千克的苹果,已知容器的底面积为0.01米2。
求:(1)苹果受到的浮力;
(2)苹果排开水的体积;
(3)若将苹果缓慢从容器中取出(苹果带出的水忽略不计),则容器底受到水的压强变化了多少?
参考答案
一.阿基米德原理的应用(共4小题)
1.【解答】解:①分析比较实验序号1与2与3的数据中V露随V物的变化关系及相关条件可知,物体的密度和液体的密度是相同的,物体都漂浮在液面上,物体的体积越大,物体漏在液面外的体积越大,所以结论为:漂浮在液面上的实心物体,当ρ液和ρ物相同时,露随V物的增大而增大;
②探究V露与ρ液的关系时需要控制物体都处于漂浮状态,物体的密度和物体的体积都相同,改变液体的密度,所以应该分析比较实验序号4与5或6和7的数据,根据数据可知,当ρ物和V物相同时,V露随ρ液的增大而增大;
③研究V露随ρ物的变化关系时,根据控制变量法可知,需要控制物体漂浮,液体的密度不变,物体的体积不变,改变物体的密度,所以需要对比2与6的实验数据;
④根据实验序号1可知:==;==;
根据实验序号2可知:==;==;
……
根据实验序号5可知:==;==;
……
根据实验序号7可知:==;==;
由此可知,=1﹣;
第8组数据中:=1﹣,代入数据得:=1﹣,解得:V露=8×10﹣6m3。
故答案为:①V露随V物的增大而增大;②4与5或6和7;③2与6;④8。
2.【解答】解:
(1)在验证阿基米德原理的实验中,根据称重法可知,(F1﹣F2)表示浸在液体里的物体所受浮力,(V2﹣V1)表示排开液体的体积;
(2)分析比较实验序号1与2与3(或5与6与7)的实验数据可初步得出的结论为:当液体密度相同时,物体受到的浮力与排开液体的体积成正比,排开液体的体积越大,物体受到的浮力越大;
(3)从表中数据可知,序号为1与5的实验中排开液体的体积都是50cm3,第5次实验中液体的密度大于第1次实验中液体的密度,第5次实验物体受到的浮力较大,符合题目要求,
同理,实验序号2和6的数据也符合要求;
(4)在第4次实验中,F2为0,说明弹簧测力计没有提起物体,可能是物体碰到了容器底部。
故答案为:(1)排开液体的体积;
(2)当液体密度相同时,物体受到的浮力与排开液体的体积成正比,排开液体的体积越大,物体受到的浮力越大;
(3)1与5(或2与6);
(4)物体碰到了量筒底部。
3.【解答】解:(1)该物体A受到的浮力:
F浮=G﹣F=19.6N﹣4.9N=14.7N;
(2)根据F浮=ρ液gV排可得排开水的体积:
V排===1.5×10﹣3m3;
由于物体处于浸没状态,则物块A的体积V物=V排=1.5×10﹣3m3。
答:①物块A受到的浮力F浮=14.7N。
②物块A的体积V物=1.5×10﹣3m3。
4.【解答】解:(1)由ρ=可得,这组气球内的氮气质量:
m氮=ρ氮V氮=ρ氮V气球=0.18kg/m3×10m3=1.8kg;
(2)这组气球在空气中所受的浮力:
F浮=ρ空气gV排=ρ空气gV气球=1.29kg/m3×10N/kg×10m3=129N;
(3)若忽略货物在空气中所受的浮力,且轻质气球本身的质量可忽略,
则该组气球所能提升货物的最大重力:
Gm最大=F浮﹣G氮=F浮﹣m氮g=129N﹣1.8kg×10N/kg=111N。
答:(1)这组气球内的氮气质量为1.8kg;
(2)这组气球在空气中所受的浮力为129N;
(3)若忽略货物在空气中所受的浮力,该组气球所能提开货物的最大重力为111N。
二.浮力大小的计算(共2小题)
5.【解答】解:(1)根据题意可知,长方体的重力G=24.5N,长方体浸没在水中时弹簧测力计示数F′=14.7N,
则该物体在水中受到的浮力:
F浮=G﹣F′=24.5N﹣14.7N=9.8N;
(2)根据F浮=F向上﹣F向下可知:
下表面所受压力F向上=F浮+F向下=9.8N+10N=19.8N;
(3)由于长方体浸没时排开液体的体积和本身的体积相等,
由F浮=ρgV排可得,该长方体的体积:
V=V排===1×10﹣3m3;
则长方体质量:
m===2.5kg,
长方体密度:
ρ===2.5×103kg/m3。
答:(1)该石块浸没在水中时受到的浮力为4.9N;
(2)下表面所受压力为19.8N;
(3)该长方体的密度为2.5×103kg/m3。
6.【解答】解:①由图象知,当h=0时,此时测力计的示数等于圆柱体的重力,所以G=F1=9.8N;
当深度为h时,测力计的示数不变,说明圆柱体完全浸没;F2=1.96N,
所以F浮=F1﹣F2=9.8N﹣1.96N=7.84N;
物体排开液体的体积V排=V物=10﹣2m3×0.1m=1×10﹣3m3
由F浮=ρ液gV排得,
ρ液===0.8×103kg/m3
②圆柱体未浸入时h液=0.2m,
筒底受到的液体压强p液=ρ液gh液=0.8×103kg/m3×9.8N/kg×0.2m=1568Pa;
③液体的质量m液=ρV液=ρ2S×2h=4ρSh,
G液=m液g=4ρShg,
圆柱体浸没时,F浮=ρ液gV排=ρgSh,
所以,对桌面的压力F桌=G液+F浮=4ρShg+ρgSh=5ρgSh,
∴压强p桌===2.5ρgh。
答:①圆柱体浸没时所受浮力F浮=7.84N;筒内液体的密度ρ液=0.8×103kg/m3;
②圆柱体未浸入时筒底受到的液体压强p液=1568Pa;
③圆筒对桌面的压强p桌=2.5ρgh。
三.探究影响浮力大小因素的实验(共20小题)
7.【解答】解:①实心柱体A高H为20cm,从柱体A接触水面开始到液面到柱体下表面深度为14cm时,弹簧测力计示数F逐渐变小,得到的结论:同一柱体逐渐浸入柱形容器内的水中,当h小于H时,液面到柱体下表面越深,弹簧测力计示数越小。
②由表一数据知,物体重力G与F的差值△F与液面到柱体下表面的距离h的比值是0.5N/cm,说明物体重力G与F的差值△F与液面到柱体下表面的距离h成正比。
③由第一次实验数据知,实心柱体刚刚接触水面,弹簧测力计测量柱体重力大小,重力大小是8N。
物体重力G与F的差值△F实际上是水对柱体的浮力,浮力大小等于水对柱体向上和向下的压力差,此时柱体没有浸没,水对柱体向下的压力为零,所以浮力大小等于水对柱体向上的压力,即F压=△F=5N。
④根据②中分析知,△F与液面到柱体下表面的距离h的比值是0.5N/cm,当h=16cm时,△F为8N,浮力等于重力,柱体在h=16cm时,柱体就漂浮在水面上,当h=18cm,h=20cm时,弹簧测力计是都没有示数,所以小明认为实验无法进行,小明的观点是正确的。
故答案为:①液面到柱体下表面越深,弹簧测力计示数越小;②重力和弹簧测力计的差值与液面到柱体下表面的距离成正比;③8;5;④正确;当h=16cm时,柱体已经漂浮在水面上,h>16cm时,弹簧测力计示数都为零。
8.【解答】解:(1)1与4、2与5、3与6的重力相同,物体的密度不同,且密度越大,压力越大,可得当物体的重力相同时,浸没在水中的物体对容器底的压力随物体密度的增大而增大;
(2)1、2、3(或4、5、6,或7、8、9)中的数据,压力与重力的比值相同,为一定值,可得当物体的密度相同时,浸没在水中的物体对容器底的压力与物体的重力成正比;
(3)(a)经计算得,第一组F与G的比值为1:2,第二组F与G的比值为3:5,第三组F与G的比值为2:3;
(b)ρ=4g/cm3,则(ρ﹣ρ水):ρ==3:4,
由表格中数据知,F:G=(ρ﹣ρ水):ρ,所以F:G=3:4,则F=×12N=9N。
故答案为:(1)1与4(或2与5,或3与6);(2)当物体的密度相同时,浸没在水中的物体对容器底的压力与物体的重力成正比;(3)(a)1:2;3:5;2:3;(b)9。
9.【解答】解:①1、2、3、4、5或6、7、8、9、10都是同种材料,由1、2、3、4、5数据可知,露出水面的体积与物块的体积比值总等于3:5,6、7、8、9、10的数据可知,露出水面的体积与物块的体积比值总等1:5,可得同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比;
②序号1与7、3与8的数据,物体的材料不同,体积相同,甲的密度较小,露出水面的体积较大,乙的密度较大,露出水面的体积较小,可得体积相同的不同材料的物块漂浮在水面上,材料密度小的物块,露出水面的体积大;
③(a)对于甲材料制成的物体,露出水面体积与物体体积的比值都是3:5,对于乙材料制成的物体,露出水面体积与物体体积的比值都是1:5,可得同种材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例相等;
(b)甲材料的密度小于乙材料的密度,但得出露出水面的体积与物体体积的比例大于乙材料露出水面的体积与物体体积的比例。
故答案为:①1、2、3、4、5或6、7、8、9、10;②体积相同的不同材料的物块漂浮在水面上,材料密度小的物块,露出水面的体积大;③(a)同种材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例相等;(b)不同材料的物块漂浮在水面上时,露出水面的体积与物体体积的比例不相等,且材料密度大的比例小。
10.【解答】解:①根据实验序号1与2与3或5与6与7的数据,分析比较弹簧测力计的示数F与圆柱体的下表面到液面的深度h的大小关系,可得出的初步结论是:同一物体在同种液体中,弹簧测力计示数F随圆柱体的下表面到液面的深度增大而减小;
②纵向比较表一序号1与2与3或表二序号5与6与7的数据,可知,圆柱体的下表面到液面的深度h为原来的几倍,△F也为原来的几倍,可得出的初步结论是:同一物体在同种液体中,△F与圆柱体的下表面到液面的深度h成正比;
③ρA=1.0×103kg/m3>ρB=0.8×103kg/m3,
根据实验序号1与5或2与6或3与7的数据,可得出的初步结论是:同一物体在不同液体中,圆柱体的下表面到液面的深度h不变时,液体密度ρ越大,△F越大;
④F0=G,根据称重法测浮力,△F=F0﹣F,
故本实验中,圆柱体的重力为:G=△F+F=1.5N+8.5N=10.0N;
由②,比较表一序号1与2与3或表二序号5与6与7的数据,可知同一物体在同种液体中,△F与圆柱体的下表面到液面的深度h成正比;但序号4与8实验不符合这个规律;
根据阿基米德原理,F浮=ρ液gV排,在物体没有浸没时,F浮=ρ液gSh,故受到的浮力与圆柱体的下表面到液面的深度h成正比,
浸没在液体中的物体受到的浮力与深度无关,说明4与8这两种情况下,圆柱体已浸没在液体中了,
由阿基米德原理:
1、4两次实验受到的浮力之比为:=,则:h=×3cm=10cm。即圆柱体的高度为10.0厘米。
故答案为:①弹簧测力计示数F随圆柱体的下表面到液面的深度增大而减小;②△F与圆柱体的下表面到液面的深度h成正比;③同一物体在不同液体中,圆柱体的下表面到液面的深度h不变时,液体密度ρ越大,△F越大;④10.0;10。
11.【解答】解:①先使鸡蛋在两种液体中浸没,根据控制变量法,鸡蛋排开液体的体积不变,而水与盐水的密度不同,鸡蛋在盐水中上浮(后漂浮),在水中沉底,所以浮力大小与液体密度有关;
②(a)分析表一实验序号3、4的数据,同一物体浸入同一液体中,当浸入液体体积相同时,浮力F不变,与h不成正比;
(b)根据表一得出得结论:同一物体浸入同一液体中,当浸入液体体积相同时,浮力F不变,与h无关,所以对比表二实验序号7,得出实验序号8的数据:浸入体积V=60厘米3,浮力F=50N;
(c)分析比较表一和表二中的数据,实验序号1、5(或2、6,或3、7),得出结论:同一物体浸入不同液体中,浸入相同体积,所受浮力不同;
③为了使实验结论具有普遍性,防止偶然性,换用其他物质(如其他材质的金属块),仍在液体A或B中进行实验;
A选项变化的量是液体密度,在上述实验序号1、5(或2、6,或3、7)已经探究过,故不合题意;
B选项变化的量是浸入的深度,在表一实验序号3、4已经探究,故不合题意;
C选项变化的量是固体的密度,前面的实验中没有探究,所以实验有意义,符合题意;故选C。
故答案为:①液体的密度;
②(a)3、4;同一物体浸入同一液体中,当浸入液体体积相同时,F与h不成正比;(b)60;0.50;(c)浸入相同体积,所受浮力不同;
③C。
12.【解答】解:(1)比较实验序号2~7数据,随着圆柱体下表面到水面距离h的增大,水对容器底部压力的增加量△F水在逐渐变大,说明在底面积不变时,当圆柱体浸入水中的深度越深,则水对容器底部的压力越大;
(2)分析实验序号2~7数据数据,圆柱体受到的浮力F浮的值都等于圆柱体下表面到水面的距离h的4倍,说明物体所受浮力的大小与物体浸入液体的深度成正比关系;
(3)比较实验序号8~9数据发现,△F水、F浮不再随h的变化而变化,说明物体已完全浸入水中,物体浸入水中的体积不再发生变化;
(4)容器上半部分的圆柱横截面积小于下半部分的,当物体开始进入水中,液体具有流动性,对容器内壁压力不同,平衡了物体所受的力,因此,分析实验序号5~9数据得出的结论与分析实验序号2~4数据得出的结论不符;
(5)根据实验数据,△F水呈现的两种不同变化关系与容器的形状有关,容器是由上、下两个横截面积不同的圆柱形构成的,实验中第2~4组数据,△F水的变化比率为0.2,实验第5~9组数据,△F水的变化比率为0.7,则上下面积之比为2:7。
故答案为:(1)随着圆柱体浸入水中深度越深,水对容器底部压力越大;(2)随着圆柱体浸入水中深度越深,圆柱体受到水的浮力越大;(3)圆柱体全部浸入水中;(4)容器上下横截面积不同;(5)2:7。
13.【解答】解:
(1)由图c可知,弹簧测力计下竖直挂着石块,是用测力计测量石块的重力;
(2)由图可知,图c测出了石块的重力,图d测出了石块浸没在液体中时测力计的拉力,图b测出空桶的重力,图e测出桶和石块排开液体的重力;
则物体浸入液体时受到的浮力为F2﹣F3,物体排开液体的重力为F4﹣F1,
如果F2﹣F3=F4﹣F1时,即物体浸在液体中受到的浮力等于物体排开液体的重力,阿基米德原理就成立。
(3)A.图(a)中溢杯内未盛满水,则测得排开水的重力会偏小,会影响验证结果。
B.图(b)中小桶内有少量水,石块排开水后,小桶重力的两次示数之差仍为排开水的重力,不影响实验结果。
C.图(d)中石块未浸没水中,此时浮力小,排开的水的体积也小,不影响实验结果。
故答案为:(1)弹簧测力计;重力;(2)F2﹣F3=F4﹣F1;(3)A。
14.【解答】解:(1)对溢水杯整体受力分析知,整体受竖直向下的重力、竖直向上的支持力、竖直向上的拉力,即G=F1+F2,
当G不再变化时,则溢水杯不再溢水,由表可知1、2、3次实验F1+F2的和都是28.5N,第4次F1+F2的和是28N,说明有水溢出,从第5s开始F1+F2的和都是27.5N,
综合分析从实验序号3开始,溢水杯内水面不再上升;在整个实验过程中,共溢出水28.5N﹣27.5N=1N;
(2)由表格数据知从1~4次实验,弹簧测力计的示数逐渐减小,说明合金块没有全部浸没,
5、6两次弹簧测力计的示数保持7.5N不变,说明合金块全部浸没了,
到第7次弹簧测力计的示数又减小了,说明合金块已经碰到容器底且容器底对物体有支持力了,故第7次的合金块下表面到溢水杯底部的距离h=0cm;
(3)①由3~6次实验数据可知,此时溢水杯内水的体积加上合金块排开水的体积刚好到溢水口,
根据物体间力的作用是相互的,合金块受到浮力等于合金块对水的压力,由阿基米德原理原理可知,合金块受到的浮力等于排开水的重力,
因此此时溢水杯中水的重力和合金块对水的压力之和等于仅在溢水杯中装水至溢水口时水的重力,
由题意可知,不计溢水杯的重力,所以此时台称的示数F2等于仅在溢水杯中装水至溢水口时水的重力,由表中3~6次实验数据可知,仅在溢水杯中装水至溢水口时水的重力为20.0N;
则溢水杯对水平面的压强:p====2000Pa,
因为轻质薄壁柱形容器对水平面的压强与液体对容器底部的压强相等,所以此时水对容器底部的压强:p水=p=2000Pa,由p=ρ水gh可得,溢水杯溢口到杯底的深度:h===0.2m;
②由5~6两次实验数据可知,合金块浸没时弹簧测力计的示数为7.5N,
由3~4两次实验数据可知,合金块每下降0.01m,弹簧测力计的示数减少0.5N,则合金块从第3次实验开始下降到刚好浸没时,弹簧测力计的示数减小了8.5N﹣7.5N=1N,此时合金块下降的距离为0.02m,因此合金块刚好浸没时,合金块下表明到溢水杯底的距离为0.10m,所以合金块的高度:h金=0.20m﹣0.10m=0.10m;
由3~4两次实验可知,合金块从第3次实验下降到第4次实验下降的高度:Δh=0.12m﹣0.11m=0.01m,增加的浮力:ΔF浮=8.5N﹣8.0N=0.5N,
由F浮=ρ液gV排可知,此时合金块排开水的体积增加量:ΔV排===5×10﹣5m3,
所以合金块的横截面积:S金===5×10﹣3m2,
所以合金块的体积:V金=S金h金=5×10﹣3m2×0.10m=5×10﹣4m3;
③合金块浸没在水中时V排=V金=5×10﹣4m3,此时合金块受到的浮力:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N,
第5、6两次实验中,合金块浸没在水中,此时合金块受到竖直向下的重力、竖直向上的浮力和拉力,
所以合金块的重力:G金=F浮+F1=5N+7.5N=12.5N,
合金块的质量:m金===1.25kg,
则合金块的密度:ρ金===2.5×103kg/m3。
故答案为:(1)3;1;(2)0;(3)2.5×103kg/m3。
15.【解答】解:①分析比较表中实验序号1~4的数据可知,随着圆柱体下降的深度越深,弹簧测力计的示数F1越来越小,台秤的示数F2越来越大,因此可得初步结论:圆柱体在浸入水的过程中,F1减小,F2增大。
②由表可以看出,在序号5、6两次实验中,弹簧测力计的示数F1不变、台秤的示数F2也不变,说明圆柱体受到的浮力不变,根据F浮=ρ液gV排可知,物体排开水的体积不变,则说明物体已全部浸没在水中。
③由表中的实验数据可得,任意两次实验中F1的减小量等于对应F2的增加量,在5、6两次实验中F1没有发生改变,F2也没有发生改变,因此可得出的结论是:圆柱体在水中缓慢下降的过程中,△F1=△F2。
取序号3、4两次实验,可得弹簧测力计F1的变化量为△F1=7.1N﹣6.8N=0.3N
则可得圆柱体在这两次实验中受到浮力的变化量为△F浮=△F1=0.3N
圆柱体的底面积为S,圆柱体下降的深度变化量为△h=4.0cm﹣3.0cm=1cm=0.01m
由阿基米德原理可得:
△F浮=ρ液g△V排=ρ液gS△h=1.0×103kg/m3×10N/kg×S×0.01m=0.3N,
解得:S=0.003m2;
由表格可知,当物体下降的深度为5cm时,物体已经完全浸没在水中,则有V排=V=Sh
圆柱体所受到的浮力为:
F浮=ρ液gV排=ρ液gSh=1.0×103kg/m3×10N/kg×0.003m2×0.05m=1.5N,
此时物体继续下降,但是受到的浮力不变,因此当圆柱体处于实验序号6的位置时,圆柱体受到的浮力为1.5N。
故答案为:①减小;增大;
②5、6;③△F1=△F2;1.5。
16.【解答】解:
①分析比较实验序号1与3(或5与6或7与9)的实验数据及相关条件知:圆柱体底面积相同,质量m不同,且质量越大,圆柱体底部到液面的深度h越大;故得出的结论是:圆柱体底面积相同,质量m越大,圆柱体底部到液面的深度h越大。
②分析比较实验序号2与3(或7与8)的实验数据及相关条件知,圆柱体质量m和体液密度ρ都相同,圆柱体的底面积S不同,且S越小,圆柱体底部到液面的深度h越大,故他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体质量m和体液密度ρ相同时,圆柱体的底面积S越小,圆柱体底部到液面的深度h越大。
③研究圆柱体的底部到液面的深度h与液体密度ρ的关系时,要控制圆柱体的质量和圆柱体的底面积相同
,只改变液体的密度,故分析比较2
与
4(或
3
与
8
或
6
与
9)实验序号的实验数据及相关条件,他们归纳得出的初步结论是:漂浮在液面上的圆柱体,圆柱体的质量m和底面积S相同,液体密度ρ越大,圆柱体的底部到液面的深度h越小。
④a、三个小组的同学对表格中的数据计算之后,进一步综合归纳结论,
a.实验2中有:=0.25
m;
实验5中有:=0.25m;
实验9中有:=0.25m;
2、5、9实验液面的深度h均为0.25m,
即圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相同,
同理,3与6或4与8圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值分别为0.3m和0.2m,
即圆柱体的底部到液面的深度h相同;
分析比较实验数据2、5与9或3与6或4与8可归纳得出的结论是:漂浮在液面上的圆柱体,圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相,圆柱体的底部到液面的深度h相同;
b、而2、5、9圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值0.25m,2、5、9实验液面的深度h均为0.25m;
3与6或4与8圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值分别为0.3m和0.2m,
而3与6或4与8实验液面的深度h分别为0.30m和0.20m,
因0.3m<0.25m<0.2m,
0.30m<0.25m<0.20m,
故得出的结论是:圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大,圆柱体的底部到液面的深度h越大;
⑤因圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大(小),圆柱体的底部到液面的深度h越大(小),故驳船载重小并且底部设计比较宽大,主要是为了减少驳船底部到液面的深度,避免搁浅的发生。
故答案为:
①圆柱体底面积相同,质量m越大,圆柱体底部到液面的深度h越大;
②圆柱体质量m和液体密度ρ相同时,圆柱体的底面积S越小,圆柱体底部到液面的深度h越大
③2
与
4(或
3
与
8
或
6
与
9);
④a.圆柱体质量m与圆柱体底面积S和液体密度ρ乘积的比值相同;
b.圆柱体质量
m
与圆柱体底面积
S
和液体密度ρ乘积的比值越大,圆柱体的底部到液面的深度h越大
⑤驳船底部到液面的深度。
17.【解答】解:①根据1与2或3与4或5与6中的实验数据,可知放入物块的重力G不相同,竖直向下的压力F相同,由实验现象可知,G越大,V浸越大;由此可知,浮在水面上的物块,F相同,G越大,V浸越大;
②由实验结论:浮在水面上的物块,当物块所受重力G相同时,F越大,V浸越大。可知,观察序号1、3、5或2、4、6的实验现象并分析V浸和G、F的关系得出的;
(a)观察实验序号2与3的实验现象,可知:浮在水面上的物块,当V浸相同时,6N+3N=3N+6N
同理,4与5中的实验现象,当V浸相同时,6N+6N=3N+9N;
由此可知:浮在水面上的物块,当V浸相同时,G+F相同(G与F之和相同)。
(b)实验序号2与3中G+F=6N+3N=3N+6N=9N;
4与5中G+F=6N+6N=3N+9N=12N,
观察实验现象可知,4与5中比序号2与3中V浸大。
因此观察实验序号2与3和4与5中的实验现象,分析V浸和G、F的关系,
由此可得:浮在水面上的物块,G+F越大(G与F之和越大),V浸越大。
故答案为:①F相同,G越大,V浸越大;1、3、5或2、4、6;
②(a)G+F相同(G与F之和相同);(b)G+F越大(G与F之和越大),V浸越大。
18.【解答】解:①在实验的过程中,为了获得普遍的规律,应选用不同体积的物体进行探究,故应选多个物体进行实验;根据控制变量法可知,实验中应控制应控制浸入水中的体积相同;
②由表格中的1和4或2和5中的数据可知,物体的体积不同,浸入水中的体积相同,浮力相同,故F浮与V物无关;
根据序号1和2和3中的实验示意图及数据可知,同一个物体,浸入水中的体积越大,受到的浮力越大,即结论是:同一物体浸入水中,物体浸入水中的体积越大,受到的浮力越大;
③由图可知,上表面没有浸入水中,则上表面受到的水的压力F上=0;
下表面受到的压强为:p下=ρgh3;下表面受到的压力为:F下=p下S=ρgh3S;
则物体受到的浮力为:F浮=F下﹣F上=ρgh3S﹣0=ρgh3S。
故答案为:①多个;相同;②1和4或2和5;物体浸入水中的体积越大,受到的浮力越大;③F浮=F下﹣F上=ρgh3S﹣0=ρgh3S。
19.【解答】解:①分析比较表一或表二中ρ物、V露的数据及相关条件,可以看出,物体的密度越大,其浸入液体中的体积也越大,V露的就越越小;故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物越大时,V露越小。
②分析比较实验序号1、4或2、5或3、6中ρ物、V浸的数据及相关条件,可以看出,当物体的密度相同时,液体的密度越小,物体排开液体的体积越大,故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V浸越大,V露越小;
③进一步分析实验序号2和4中的数据及相关条件,可以看出,物体密度与液体密度的比值都是1:2,这时它们在液体中排开液体的体积是相同的。因此,得出的合理猜想是:漂浮在液面上体积相同的物块,当ρ物与ρ液的比值相同时,V浸是相同的:
第一组:ρ物=×1.5克/厘米3=0.3克/厘米3。
第一组:ρ物=×1克/厘米3=0.4克/厘米3。
故答案为:(1)当ρ物越大时,V露越小;②1、4或2、5或3、6;③0.3;0.4。
20.【解答】解:
(1)探究物体所受浮力的大小和物体排开液体体积的关系时,需要控制液体的密度和物体所在的深度一定,排开液体的体积不同,故需要对比的是图(a)、(b)、(c);
(2)选用的图(a)、(d)、(e)对比时,物体排开的液体的体积相同,液体的密度不同,所以探究的是物体所受浮力的大小和液体密度的关系;根据图可知,液体的密度不同,浮力不同,液体密度越大,受到的浮力越大,故可以得出结论:物体排开液体体积一定时,液体的密度越大,浮力越大;
(3)本实验采用了控制变量法。
故答案为:(1)(a)、(b)、(c);(2)浮力大小与液体密度的关系;物体排开液体体积一定时,液体的密度越大,浮力越大;(3)控制变量。
21.【解答】解:由题意,探究步骤(二):探究h与正方体物块的密度ρ物的关系
4、①你认为探究步骤(一)中需要改进的地方是:缺少记录实验数据的表格。
②“探究步骤(二):
探究h与正方体物块的密度ρ物的关系;
③由表中数据知:物块的密度越大,露出液面的高度越小;
④由表中数据知:物块的密度每增大200kg/m3,露出高度就减小2cm;
所以,可以推测:物块的密度增大到1000kg/m3时,露出水面的高度减小为零,
即:若露出水面的高度为零时,物块的密度ρ物与水的密度ρ水的比值等于1:1。
⑤正方体的体积为H3;
正方体液面下的长度为H﹣h,排开液体的体积为V排=H2(H﹣h),
根据阿基米德原理,正方体受到的浮力:
F=ρ液gV排=ρ液gH2(H﹣h),
根据漂浮的特点,F=G=ρ物gH3;
即ρ液gH2(H﹣h)=ρ物gH3
故关于正方体物块露出液面的高度h与它的边长H的比值:
=,故选C。
故答案为:探究h与正方体物块的密度ρ物的关系;
(4)①缺少记录实验数据的表格;
②正方体物块的密度ρ物;
③物块的密度越大,露出液面的高度越小;
④1:1;
⑤C。
22.【解答】解:
①分析比较实验序号2与3与4(或8与9与10)数据中△F和h的数据知,除1、7处,圆柱体下表面到液面的距离h增大为原来的几倍,F的变化量△F也增大为原来的几倍,故可得出的初步结论是:同一圆柱体浸入同种液体过程中,△F和h成正比;
②ρ1<ρ2,分析比较实验序号2与8(或3与9或4与10或5和11)数据中△F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入不同液体过程中,h相同时,液体密度越大,△F越大;
③小明和小华继续分析表一、表二数据中F和h的关系,并进行相关思考。
(a)分析比较实验序号1~5(或7~11)数据中F和h的关系及相关条件,可得出的初步结论是:同一圆柱体浸入同种液体过程中,F随h的增大而减小;
(b)分析比较实验序号5和6(或11和12)数据中F和h的关系及相关条件可知,当h≥H时,F不再随h的变化而变化,为验证该观点,他们换用高H为15厘米的圆柱体B继续实验,初步证明小明正确,据此表完成表三中的数据,如下所示:
实验序号
h(厘米)
F(牛)
13
15
20.0
14
17
20.0
15
20
20.0
故答案为:
①△F和h成正比;
②h相同时,液体密度越大,△F越大;
③(a)同一圆柱体浸入同种液体过程中,F随h的增大而减小;如上表所示。
23.【解答】解:
①分析比较表一中△F水和相关条件,可以看出三次放入容器中的物重G不同,但△F水的增加量均为1.0N,因此可得:△F水与G物无关;
②分析比较表二中实验序号4与5与6的数据可知,物体的体积越大,容器底部受到水的压力增加量△F水越大,且△F水与V物成正比,即:△F水与V物有关;
要得出△F水与V物无关,即:V物不同时,而容器底部受到液体压力的增加量△F水相同,由表二数据可知,实验5与7符合要求;
分析比较实验序号6与7与8的数据可知,物体的体积相同,但排开水的体积不相同,容器底部受到液体压力的增加量△F水不相同,因此可以得到:影响△F水的因素可能是排开液体的体积;
为了得到普遍规律,需要换用不同密度的液体多次实验。
故答案为:
①无关;
②△F水与V物成正比;5与7;排开液体的体积;不同密度的液体。
24.【解答】解:
①在该实验中,需要测量金属块在不同液体中排开的液体的体积,所以需要用到量筒;由图可知,金属块在空气中的重力示数为F1,由表格中的数据可知,金属块的重力为4N;
②a.根据实验序号1与2中ρ和F2数据及相关条件可知,金属块相同,浸没在不同的液体中,弹簧测力计两次示数的差值F1﹣F2为浮力的大小;液体的密度越小,弹簧测力计示数F2越大,则金属块所受的浮力F1﹣F2越小,所以实验结论为:对浸没在液体中的同一金属块而言,液体密度越小,弹簧测力计示数F2越大,金属块所受的浮力F1﹣F2越小;
b.分析比较实验序号1、2、3中ρ和F1﹣F2数据及相关条件可知:液体的密度ρ越小,弹簧测力计示数之差F1﹣F2与越小,且弹簧测力计示数之差F1﹣F2与ρ成正比;故结论为:对浸没在液体中的同一金属块而言,弹簧测力计示数之差F1﹣F2与ρ成正比;
③实验的过程中,测量的是弹簧测力计示数之差F1﹣F2即浮力的大小;实验中还测量了金属块排开液体的重力【即G排=ρg(V2﹣V1)】,所以探究的是浮力与物体排开液体的重力的关系,即探究的是阿基米德原理;故选A;
④为了得出普遍结论,应该换用换用不同材料的金属块多次实验,从而得到正确的结论。
故答案为:①量筒;4N;
②液体密度越小,弹簧测力计示数F2越大,金属块所受的浮力F1﹣F2越小;弹簧测力计示数之差F1﹣F2与ρ成正比;
③A;
④换用不同材料的金属块多次实验。
25.【解答】解:①由题可知,圆柱体的高为0.2米,当圆柱体下表面到液面的深度h=0.18米时,圆柱体上表面在液面上方,液体对圆柱体上表面的压力F1=0,
当圆柱体下表面到液面的深度h=0.20米时,圆柱体上表面刚好处于液面的位置,液体对圆柱体上表面的压力F1=0;
②分析比较实验序号1~5数据可以看出,当一圆柱体浸入同一液体中时,深度h越大,下表面所受的压力F2越大,故可得:当一圆柱体浸入同一液体中时,F2与h成正比;
③分析实验序号3与4与5数据可以看出,当一圆柱体浸没同一液体中时,虽然深度增加,但上、下表面受到的压力差却是相等的,故可得:当一圆柱体浸没同一液体中时,△F与h无关;
④圆柱体下表面在液体中的深度、液体的密度对圆柱体下表面受到液体的压力均有影响,故圆柱体下表面受到液体的压力大小与液体密度的关系,应控制圆柱体下表面在液体中的深度不变。
故答案为:①0;0;
②当一圆柱体浸入同一液体中时,F2与h成正比;
③当一圆柱体浸没同一液体中时,△F与h无关;
④圆柱体下表面在液体中的深度。
26.【解答】解:①由表中数据1与6或4与8可知,柱形物体浸入液体中,物体所受浮力相同,容器对桌面压力相同;
②分析表一、表二中实验序号5与8的数据,物体接触到了容器底,同时又受到了容器底的支持力,故与小林得出结论不符;
③分析实验序号1、2、3、4或6、7、8、9可知,同一柱形物体浸入同一柱形容器的液体中,F桌的变化量等于F浮的变化量;
④进一步分析实验序号1~5或76~10数据可得,同一物体浸入液体中,测力计示数F与容器对桌面的压力F桌之和是相同的,
故当测力计示数F为8N时,F桌的大小为90N﹣8N=82N。
故答案为:①1、6或4、8;②容器底对物体有向上的支持力;③同一柱形物体浸入同一柱形容器的液体中,F桌的变化量等于F浮的变化量;④82。
四.物体的浮沉条件及其应用(共4小题)
27.【解答】解:
①分析比较表一或表二中ρ物、V露的数据及相关条件,可以看出:当ρ液相同时(即用同种液体做实验),物体的密度越大,露出液面的体积V露越小;故可得出的初步结论是:漂浮在液面上体积相同的物块,当ρ液相同时,ρ物越大时,V露越小。
②要得出结论“漂浮在液面上体积相同的物块,当ρ物相同时,ρ液越小,V露越小”,根据控制变量法,应控制物体的密度相同,由表格数据可知,应分析比较实验序号1、4或2、5或3、6中ρ物、V浸的数据及相关条件;
③进一步分析实验序号2和4中的数据及相关条件,可以看出:虽然ρ物与ρ液均不同,但物体密度与液体密度的比值相同(都是1:2),这时V露是相同的(都是50.0厘米3)。
因此,得出的合理猜想是:漂浮在液面上体积相同的物块,当ρ物与ρ液的比值相同时,V露是相同的:
表三中,第一组:=,则ρ物=×1.5g/cm3=0.3g/cm3。
同理可得第二组:ρ物′=×1g/cm3=0.4g/cm3。
故答案为:
(1)当ρ液相同时,ρ物越大时,V露越小;(2)1、4或2、5或3、6;(3)0.3;0.4。
28.【解答】解:(1)∵空心铜球悬浮在水中:
V排=v=17.8cm3=17.8×10﹣6m3,
∴F浮=ρ水gV排
=1.0×103kg/m3×10N/kg×17.8×10﹣6m3
=0.178N;
∵小球悬浮时,浮力等于其重力,
∴G=F浮=0.178N。
答:(1)空心铜球的重力为0.178N;
(2)∵,
∴铜球的实心部分的体积:
=2×10﹣6m3=2cm3。
铜球中空心部分的体积:
V空=V﹣V实=17.8cm3﹣2cm3=15.8cm3。
答:铜球空心部分的体积15.8cm3。
29.【解答】解:
(1)受到的浮力为:F浮=ρ海水gV排=1×103kg/m3×10N/kg×24m3=2.4×105N;
(2)由阿基米德原理F浮=ρ海水gV排可知,物体在液体中所受的浮力大小只与液体的密度和排开液体的体积有关,与其它因素都无关。当抹香鲸继续下潜至2000米深的海底时,因为水密度不变,排开水的体积不变,所以受到的浮力不变。
答:(1)潜至此深度时,抹香鲸所受到的浮力大小F浮=2.4×105N。
(2)若抹香鲸继续下潜至2000米深的海底,它受到的浮力不变。原因是水密度不变,排开水的体积不变,根据F浮=ρ海水gV排可知其受到的浮力不变。
30.【解答】解:(1)G=mg=0.2kg×10N/kg=2N;
因为苹果漂浮
所以F浮=G=2N;
(2)由F浮=ρ液V排g可得,苹果排开水的体积:
V排===2×10﹣4m3;
(3)水降低的高度△h===2×10﹣2m;
容器底受到水的压强减少:
△p=ρg△h=1.0×103kg/m3×10N/kg×2×10﹣2m=200Pa。
答:(1)苹果受到的浮力大小为2牛。
(2)苹果排开水的体积为2×10﹣4m3。
(3)若将苹果缓慢从容器中取出(苹果带出的水忽略不计),则容器底受到水的压强减少了200Pa。
