2021-2022学年上学期上海市沪教版九年级物理同步巩固复习作业—01密度(含答案解析)
文档属性
| 名称 | 2021-2022学年上学期上海市沪教版九年级物理同步巩固复习作业—01密度(含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 501.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(试用本) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-26 20:37:27 | ||
图片预览




文档简介
目录
TOC
\o
"1-1"
\h
\u
一.密度及其特性(共2小题)
1
二.密度的大小比较(共2小题)
2
三.密度的计算(共4小题)
2
四.密度公式的应用(共20小题)
3
五.固体密度的测量(共1小题)
10
六.液体密度的测量(共1小题)
10
七.空心、混合物质的密度计算(共3小题)
10
八.探究密度特性的实验(共6小题)
11
九.固体的密度测量实验(共1小题)
13
参考答案及解析
15
目录
15
一.密度及其特性(共2小题)
15
二.密度的大小比较(共2小题)
15
三.密度的计算(共4小题)
16
四.密度公式的应用(共20小题)
18
五.固体密度的测量(共1小题)
29
六.液体密度的测量(共1小题)
29
七.空心、混合物质的密度计算(共3小题)
29
八.探究密度特性的实验(共6小题)
31
九.固体的密度测量实验(共1小题)
33
一.密度及其特性(共2小题)
1.小明同学阅读下表后,得出了一些结论,其中正确的是( )
一些物质的密度/Kg?m﹣3
水
1.0×103
水银
13.6×103
冰
0.9×103
松木
0.5×103
煤油
0.8×103
铜
8.9×103
酒精
0.8×103
铅
11.3×103
A.不同的物质,密度一定不同
B.固体的密度都比液体的大
C.质量相等的实心铜块和实心铅块,铜块的体积比铅块的体积小
D.同种物质在不同状态下,其密度不同
2.如图所示是某实验小组的同学用甲、乙两种不同的物质做实验时得到的m﹣V图线。根据图线可判断( )
A.ρ甲<ρ乙<ρ水
B.ρ甲<ρ乙=ρ水
C.ρ甲>ρ乙=ρ水
D.ρ甲>ρ乙>ρ水
二.密度的大小比较(共2小题)
3.如图所示,均质圆柱形固体A和盛有液体的轻质柱形容器B对水平桌面的压力相等。将固体A沿水平方向切去和容器B中抽出相同的任意高度△h,剩余部分固体对桌面的压强、液体对容器底部的压强分别为PA、PB,要使PA与PB的差值始终保持不变。则它们密度的大小关系是( )
A.ρA可能大于ρB
B.ρA一定等于ρB
C.ρA可能等于ρB
D.ρA一定大于ρB
4.两个完全相同的圆柱形容器甲和乙底部相连通,给两容器分别倒入不同质量的同种液体后,将质量相同的两物块浸没在两容器中(无液体溢出),结果发现有部分液体从乙容器流入甲容器,则( )
A.甲容器中的物块的密度大
B.甲、乙容器中的物块的密度一样大
C.乙容器中的物块的密度大
D.条件不足,无法判断
三.密度的计算(共4小题)
5.某空瓶的质量为0.1千克,在瓶内装满水,测得瓶和水的总质量0.7千克,将质量为0.5千克的金属块浸没在瓶内水中,等停止溢水后再次测得瓶、金属块和剩余水的总质量1.1千克。求:
(1)瓶的容积V容。
(2)溢出水的质量m溢。
(3)金属块的密度ρ金属。
6.一个空瓶的质量为m0,装满某种液体后瓶和液体的总质量是m1.若在该空瓶中先放一些金属颗粒,使瓶和金属颗粒的总质量为m2,然后往瓶里装这种液体直至充满整瓶,用天平测得这时瓶、金属颗粒和液体的总质量为m3,这种液体的密度为ρ液,则瓶里金属颗粒的密度为多少?(请用题目中给出的字母表示,并保留公式推导过程)
7.底面积为1×10﹣2米2薄壁轻质圆柱形容器A(容器足够高)放置于水平地面上,里面盛有0.2米深的水,如图所示。将另一质量为6千克、底面积为5×10﹣3米2的实心金属圆柱体B竖直放入容器A中,待水静止后,圆柱体B上表面露出水面高度为0.1米。
求:(1)容器中水的质量。
(2)金属圆柱体B的密度。
8.如图所示,正方体甲的体积为10﹣3米3,密度为6.3×103千克/米3,正方体乙的体积为8×10﹣3米3,质量为6千克。求:
①正方体甲的质量m甲;
②正方体乙的密度ρ乙;
③若沿正方体乙的上表面挖去一底面积为0.01米2、高为h的长方体,并在挖去部分中倒满水,是否可能使乙变化后的总质量与甲的质量相等?若可能,请计算h;若不可能,请简要说明理由。
四.密度公式的应用(共20小题)
9.如图所示,底面积为正方形的实心长方体A和B放置在水平地面上。若沿竖直方向将A、B两长方体截去一部分,使长方体A、B剩余的面积相等,剩余部分质量m′A等于m′B。则关于长方体A、B的密度ρA、ρB,原来的质量mA、mB的大小关系,下列说法正确的是( )
A.ρA<ρB,mA<mB
B.ρA<ρB,mA>mB
C.ρA>ρB,mA<mB
D.ρA>ρB,mA>mB
10.如图所示,底面积不同的A、B两圆柱体容器分别盛有甲、乙两种液体,已知液体质量m甲<m乙。若在两容器中分别抽出相同高度的液体,则抽出液体的质量△m甲、△m乙和液体的体积△V甲、△V乙的关系是( )
A.△m甲<△m乙,△V甲>△V乙
B.△m甲<△m乙,△V甲<△V乙
C.△m甲>△m乙,△V甲>△V乙
D.△m甲>△m乙,△V甲<△V乙
11.如图所示,均匀圆柱体甲和盛有液体乙的薄壁薄底圆柱形容器置于水平地面,圆柱体和容器的高度相等但底面积不同,甲对地面的压力等于液体乙对容器底部的压力。现沿水平方向截取部分圆柱体甲并从容器内抽取部分液体乙,使得它们剩余部分的高度或深度均为h,则甲、乙的密度ρ以及它们截取或抽取部分质量m的关系是( )
A.ρ甲>ρ乙;m甲>m乙
B.ρ甲>ρ乙;m甲<m乙
C.ρ甲<ρ乙;m甲>m乙
D.ρ甲<ρ乙;m甲<m乙
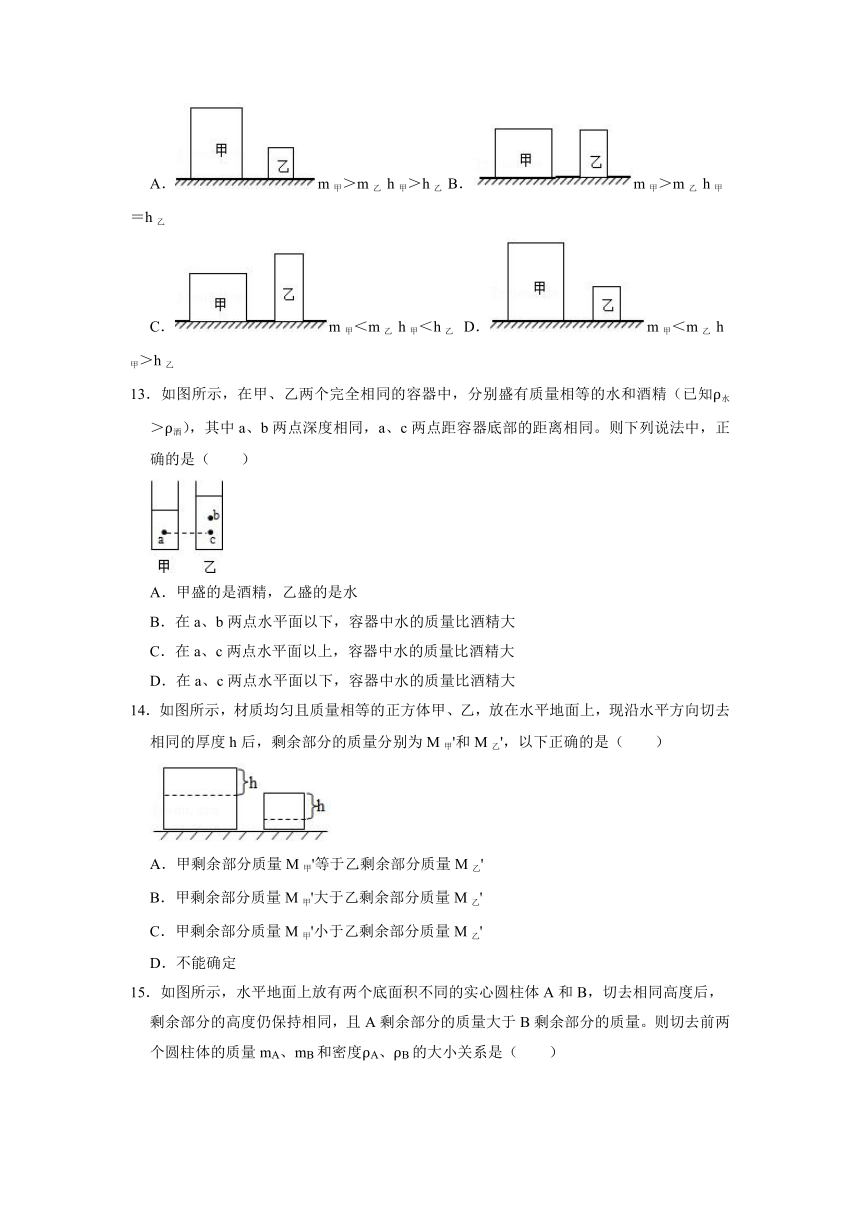
12.均匀实心圆柱体甲、乙放置在水平地面上。现在甲、乙的上方沿水平方向切去相同质量后,如图所示。甲剩余部分质量小于乙剩余部分质量。则两个圆柱体原来的情况可能是下图中的( )
A.m甲>m乙
h甲>h乙
B.m甲>m乙
h甲=h乙
C.m甲<m乙
h甲<h乙
D.m甲<m乙
h甲>h乙
13.如图所示,在甲、乙两个完全相同的容器中,分别盛有质量相等的水和酒精(已知ρ水>ρ酒),其中a、b两点深度相同,a、c两点距容器底部的距离相同。则下列说法中,正确的是( )
A.甲盛的是酒精,乙盛的是水
B.在a、b两点水平面以下,容器中水的质量比酒精大
C.在a、c两点水平面以上,容器中水的质量比酒精大
D.在a、c两点水平面以下,容器中水的质量比酒精大
14.如图所示,材质均匀且质量相等的正方体甲、乙,放在水平地面上,现沿水平方向切去相同的厚度h后,剩余部分的质量分别为M甲'和M乙',以下正确的是( )
A.甲剩余部分质量M甲'等于乙剩余部分质量M乙'
B.甲剩余部分质量M甲'大于乙剩余部分质量M乙'
C.甲剩余部分质量M甲'小于乙剩余部分质量M乙'
D.不能确定
15.如图所示,水平地面上放有两个底面积不同的实心圆柱体A和B,切去相同高度后,
剩余部分的高度仍保持相同,且A剩余部分的质量大于B剩余部分的质量。则切去前两个圆柱体的质量mA、mB和密度ρA、ρB的大小关系是( )
A.mA<mB,ρA<ρB
B.mA<mB,ρA>ρB
C.mA>mB,ρA<ρB
D.mA>mB,ρA>ρB
16.如图所示,甲、乙两个实心均匀正方形的质量相等,若沿竖直方向分别在两个正方体右侧截取相同的厚度,则甲、乙( )
A.剩余部分的质量m甲<m乙
B.剩余部分的体积V甲=V乙
C.截去部分的质量△m甲<△m乙
D.截去部分的体积△V甲=△V乙
17.如图所示,甲、乙(S甲<S乙,h甲>h乙)两个均匀实心圆柱体放在水平地面上。若在它们上部分别水平切去△h甲、△h乙后,甲和乙剩余部分的质量恰好相等。请按样例,根据△h甲和△h乙的大小关系,写出被切去部分的质量△m甲、△m乙的大小关系。
(样例:若△h甲>△h乙,则△m甲可能大于△m乙。)
18.质量为1千克的冰块全部熔化成水,水的质量为
千克,水的体积为
米3。冰的密度为0.9×103千克/米3,则水的体积
冰的体积(选填“大于”、“等于”或“小于”)。
19.冰的密度为0.9×103千克/米3,表示每立方米冰的质量为
千克。质量为0.9千克的水凝结成冰之后,冰的质量为
千克,冰的体积为
米3。
20.某同学在测量某液体的质量和体积的关系的实验中,得到了如图所示图象,其中纵坐标m表示烧杯和液体的总质量,V表示液体的体积,装液体的空烧杯的质量是
克该液体的密度是
千克/米3,图中m的值应为
克。
21.如图所示,甲、乙两薄壁圆柱形容器(容器足够高)放置在水平桌面上,甲容器底面积为9S、乙容器底面积为10S,甲中盛有深度为4h的水,乙中盛有深度为5h的酒精,为了使甲、乙两容器内水和酒精的质量相等,应
(选填“向容器中加入”或“从容器中抽出”)深度均为
的水和酒精。(ρ酒精=0.8×103kg/m3)
22.如图所示,正方体甲的边长为0.1米,体积为10﹣3米?,密度为8×10?千克/米?,正方体乙的边长为0.2米,体积为8×10﹣3米?,质量为4千克。求:
①正方体甲的质量m甲;
②正方体乙的密度ρ乙;
③若沿水平方向分别在两个正方体的上部各截下相同的厚度d,并将乙截下的部分叠放在甲剩下部分的上方,总质量记为m1,将甲截下的部分叠放在乙剩下部分的上方,总质量记为m2,若要使m1与m2的比值为0.5,请问是否存在满足要求的厚度d,若存在请求出d的取值,若不存在请通过计算说明。
23.如图所示,两个完全相同的圆柱形容器甲和乙放在水平面上(容器足够高),分别装有质量相等的水和酒精,容器的底面积为1×10﹣2米2,容器内水的深度为0.1米(已知ρ水=1000kg/m3,ρ铝=2700kg/m3,ρ冰=900kg/m3)求:
①容器甲中水的质量。
②求乙容器中酒精的体积。
③将2700克铝块浸没在酒精中,将一块冰块放入水中,质量未知的冰块全部熔化变成水时,发现两个容器中液面一样高,求冰块的质量。
24.如图所示,轻质柱形容器底面积为2×10﹣2米2,放在水平地面上,容器中盛满水时,水的质量为5千克,求:
(1)容器中水的体积。
(2)将一个体积为2×10﹣3米3、密度为2.9×103千克/米3的实心均匀物块A浸没在容器内水中后,求整个容器在物块A放入前后总质量的变化量△m。
25.如图所示,A、B两个完全相同圆柱形容器放在水平地面上,容器的底面积为2×10﹣2米2.容器A中盛有一定量的水,水面距容器底部0.1米;B容器中盛有的酒精。(ρ酒精=0.8×103千克/米3,ρ铝=2.7×103千克/米3,ρ铁=7.8×103千克/米3)求:
①A容器中水的质量m水。
②如果B容器中酒精的质量等于水的质量,求B容器中酒精的体积V酒。
③将2700克的铝块浸没在水中,质量未知的铁块浸没在酒精中,发现两个容器中液体的液面一样高(液体不溢出).求铁块的质量m铁。
26.如图所示,实心正方体A、B的边长分别是0.1米,0.2米,密度分别为ρA=2×103千克/米3,ρB=0.2×103千克/米3,求:
(1)正方体A的质量;
(2)正方体B的重力;
(3)若在正方体A、B上部沿水平方向截去相同高度h,A、B剩余的质量为mA′和mB′,请通过计算比较它们的大小关系及其对应的深度h的取值范围。
27.如图所示,两高度均为h的柱形容器甲、乙放置在水平地面上,已知甲、乙的底面积分别为2S、S.甲容器中装满有3×10﹣2米3的水。
(1)求甲容器中的水的质量;
(2)往乙容器中注入密度为ρ0的液体,则最多能注入的体积为多少。
(3)将体积为1×10﹣3米3的物体A浸没于装满水的甲容器中,将体积为2×10﹣3米3的物体B浸没于装满密度为ρ0液体的乙容器中。已知乙容器中溢出液体的质量是甲容器中溢出水质量的3倍。求密度ρ0的大小。
28.如图所示,一个容积V0=500cm3、质量m=0.5kg的瓶子里装有水,乌鸦为了喝到瓶子里的水,就衔了很多的小石块填到瓶子里,让水面上升到瓶口。若瓶内有质量m=0.4kg的水。求:(水的密度ρ水=1.0×103kg/m3,石块密度ρ石块=2.6×103kg/m3)
(1)瓶中水的体积V1;
(2)乌鸦投入瓶子中的石块的体积V2;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
五.固体密度的测量(共1小题)
29.在“测定物质的密度”实验中,用
测物块的质量时,砝码和游码的示数如图(a)所示,则物块的质量为
克;将物块放入盛有40厘米3水的量筒后,水面位置如图(b)所示,则物块的体积为
厘米3,物块的密度为
千克/米3。
六.液体密度的测量(共1小题)
30.为了测出盐水的密度,某实验小组制定了如下的实验计划:
①在烧杯中装入适量盐水,测出它们的总质量:
②将烧杯中的一部分盐水倒入量筒中:
③测出量筒中盐水的体积:
④测出烧杯和剩余盐水的质量;
⑤测出空烧杯的质量;
⑥根据实验数据计算盐水密度
以上实验步骤安排最合理的是( )
A.①②③④⑥
B.⑤①②③⑥
C.①②④③⑤⑥
D.⑤①②④③⑥
七.空心、混合物质的密度计算(共3小题)
31.用相同质量的铝和铜制成体积相等的球,已知ρ铝=2.7×103kg/m3,ρ铜=8.9×103kg/m3,则下列说法正确的( )
A.铜球是空心的,铝球也一定是空心的
B.铝球一定是实心的
C.铜球不可能是实心的
D.铝球和铜球都是实心的
32.甲、乙两个实心的正方体,它们的边长之比是1:2,密度之比是2:1,则它们的质量之比是
;已知
A、B两种金属密度为ρ1、ρ2,取质量相等的
A、B两种金属制成合金,这种合金的密度为
。
33.一只铁球的体积为40厘米3,质量为156克,铁的密度为7.8g/cm3。
(1)问:这只铁球是否空心?请计算作答
(2)若这只铁球是空心的,求空心部分的体积V空。
八.探究密度特性的实验(共6小题)
34.某同学比较“测物质密度”和“探究物质质量与体积关系”两个实验后,认为
①所测的物理量相同
②测量的工具相同③需多次测量的目的不同。他的判断正确的是( )
A.①②
B.②和③
C.①和③
D.①、②和③
35.“探究物质质量与体积关系”实验和“测定铁块的密度”实验相比较:需要测量的物理量
(选填“相同”或“不同”),实验目的
(选填“相同”或“不同”).“探究物质质量与体积关系”实验中,在研究了水的质量与体积关系后,还需要用
进行多次实验,这样做是为
。
36.某同学为了“探究物质的质量与体积的关系”,他先选用某种液体进行实验,用电子天平测出液体的
,并用量筒测出液体的
,为了进行探究,他需要改变这种液体的
进行多次实验。为了进一步研究物质的特性,他还需要选用
(选填“不同”或“相同”)种类的物质进行实验,目的是
;测物质密度实验,用
种物质,进行
实验,目的是
。
37.为了研究物质质量与体积的关系,某兴趣小组同学利用不同的金属块分别进行实验。
(1)甲同学根据“小铁钉和大铁锤的质量不同”的事实,认为“物体的质量可能跟物体的体积有关”。于是就利用仪器测得不同铁块的体积和质量,并将相关数据记录在表一中。则分析比较实验序号1和2和3中质量与体积的倍数关系,可初步得出:
。
表一
实验序号
物质
体积(厘米3)
质量(克)
1
铁
5
39
2
15
117
3
30
234
表二
实验序号
4
5
6
7
8
金属种类
铝
铜
铅
铝
铝
体积(厘米3)
10
10
20
20
30
质量(克)
27
89
226
54
81
(2)乙同学根据“家里同样的维纳斯塑像,玻璃制品和石膏制品的质量不同”的生活经验提出了合理的假设,你认为乙同学的假设应为
。于是,乙同学选用了一些金属块,并测得它们各自的体积和质量,并将相关数据记录在表二中。就表二所列的实验数据中,你认为可用的是
。(选填实验序号)
(3)为了进一步研究物质的某种特性,请你综合分析比较两表中的相关数据,并得出相应的结论:
a
。b
。
38.小静和小芳在“探究物质质量与体积的关系”实验中,分别测出几种物质的质量和体积,测量结果分别记录如表一~表三所示。
表一:塑料颗粒
表二:水
表三:酒精
实验序号
体积/厘米3
质量/克
实验序号
体积/厘米3
质量/克
实验序号
体积/厘米3
质量/克
1
20
26.0
4
35
35.0
7
24
19.2
2
30
39.0
5
44
44.0
8
30
24.0
3
40
52.0
6
50
50.0
9
40
32.0
(1)分析表一或表二或表三中物质的质量与体积变化的倍数关系,可以得出的初步结论是:
。
(2)进一步分析比较三个表中的实验数据,小静认为:同种物质,质量与体积的比值是一个不变的值;但不同物质这个比值不同。小芳认为:同种物质,体积与质量的比值是一个不变的值,但不同物质这个比值不同。你认为小静的观点
,小芳的观点
。(均选填“正确”或“错误”)
为了比较上述两个“比值”的意义,他们找了一块海绵,用手紧压海绵,发现海绵的质量不变、体积变小,说明海绵越密时,
的比值越大,海绵越疏时,
的比值越大。在上述两个比值中,
比值更能直观合理地反映物质的紧密程度。
39.为了“探究物质质量与体积的关系”,小王和小李同学分别进行实验:
(1)小王:探究液体质量与体积的关系,他选用的实验器材有:天平(带砝码)、量筒、烧杯、水和
。实验中,为了得到比较完整的结论,要进行
测量(填“一次”或“多次”)。
(2)小李同学探究固体质量与体积的关系,他选用的实验器材除天平(带砝码)、量筒、烧杯和水外,还选用了不同体积,不同质量的金属块若干。实验时,他分别测得不同金属块的体积和质量,并将相关数据记录在表中。
物质
铁
铜
铅
铝
实验序号
1
2
3
4
5
6
7
8
9
体积/厘米3
5
15
30
10
20
20
10
20
30
质量/克
39
117
234
89
178
226
27
54
81
①分析上表的实验序号l、2与3或4与5或7、8与9的体积及质量变化的倍数关系,可归纳出的初步结论是:
。
⑦分析上表中实验序号
的关系。可归纳出的初步结论是:相同体积的不同物质,它们的质量是不同的。
③请进一步综合分析比较表中的效据,并归纳得出结论。
(a)
。
(b)
。
九.固体的密度测量实验(共1小题)
40.小明在实验室里测量一块形状不规则、体积较大的矿石的密度。
(1)在使用已调节好的托盘天平,按规范的操作来称量矿石的质量时,通过增、减砝码后都不能使天平平衡,指针仍然偏在分度盘中线右边一点,这时应该
。
(2)因矿石体积较大放不进量筒,因此他利用一只烧杯,按图所示方法进行测量,则矿石的体积是
cm3
(3)用托盘天平已测得矿石的质量是175g,则矿石的密度是
千克/米3;从图A到图B的操作引起的密度测量值比真实值
(选填:“偏大”、“偏小”或“不变”)。
参考答案及解析
一.密度及其特性(共2小题)
1.【解答】解:A、表中煤油和酒精的密度均为0.8×103kg?m﹣3,故此选项错误。
B、表中松木是固体,密度小于液体水银的密度,故此选项错误。
C、根据公式V=m/ρ,质量相同时,密度越大体积越小,铜的密度小于铅的密度,故铜的体积大于铅的体积。
D、由表中数据,对于同种物质,水和冰的密度不同。
故选:D。
2.【解答】解:由图示可知:
ρ甲===1.75g/cm3;
ρ乙===1g/cm3=ρ水;
故选:C。
二.密度的大小比较(共2小题)
3.【解答】解:因为A为规则固体,B为轻质柱形容器容器,则A对桌面的压强:pA=ρAghA,B内液体对容器底的压强:pB=ρBghB,
因为A对水平桌面的压力和B对水平桌面的压力相等,而SA<SB,由p=可得,A对水平桌面的压强大于B对容器底的压强;
∴ρAghA>ρBghB
∵hA>hB
∴ρA可能大于、小于或等于ρB,
∵PA与PB的差值始终保持不变,
∴A、B的压强变化量满足△P=△PA﹣△PB=0,即ρAg△h﹣ρBg△h=0,
∴ρA=ρB。
故选:B。
4.【解答】解:发现有部分水从乙容器流入甲容器,说明放入物块后乙容器中水面比甲容器中高;因为容器完全相同,也就是说乙容器中物块排开水的体积大,因为都是浸没在两容器的水中并且水没有溢出容器外,说明乙容器中的体积大;两个物块的质量相同,乙容器中物块的体积大,根据密度的公式ρ=,所以乙容器中物块的密度小,甲容器中物块的密度大。
故选:A。
三.密度的计算(共4小题)
5.【解答】解:
(1)瓶子中装满水后水的质量:m水=0.7kg﹣0.1kg=0.6kg=600g,
由ρ=可得空瓶容积:
V=V水===600cm3;
(2)溢出水的质量:m溢=0.5kg+0.7kg﹣1.1kg=0.1kg=100g,
(3)金属块的体积:
V金=V溢===100cm3,
金属块的质量:m金=0.5kg=500g,
金属块的密度:
ρ===5g/cm3=5×103kg/m3。
答:(1)瓶的容积为600cm3;
(2)溢出水的质量为100g;
(3)金属块的密度5×103kg/m3。
6.【解答】解:空瓶装满液体时液体的质量:
m液=m1﹣m0,
由ρ=可得,空瓶的容积:
V=V液==,
金属粒的质量:
m金=m2﹣m0,
瓶中装了金属粒后再装满液体,此时瓶中液体的质量:
m液'=m3﹣m2,
此时瓶中液体的体积:
V液'==,
则金属粒的体积:
V金=V﹣V'水=﹣=,
金属粒的密度:
ρ金===。
答:瓶里金属颗粒的密度为。
7.【解答】解:(1)容器中水的体积:
V水=S容h=1×10﹣2m2×0.2m=2×10﹣3m3,
由ρ=可得,容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg;
(2)由题知,金属圆柱体放入水中后,露出水面0.1m,设此时水深为h水,
则水的体积为V水=(S容﹣S金)h水,
所以,此时的水深:
h水===0.4m,
则金属圆柱体的高度:
h金=h水+h露=0.4m+0.1m=0.5m,
金属圆柱体的体积:
V金=S金h金=5×10﹣3m2×0.5m=2.5×10﹣3m3,
金属圆柱体B的密度:
ρ金===2.4×103kg/m3。
答:(1)容器中水的质量为2kg;
(2)金属圆柱体B的密度为2.4×103kg/m3。
8.【解答】解:①由ρ=可得,正方体甲的质量:
m甲=ρ甲V甲=6.3×103kg/m3×10﹣3m3=6.3kg;
②正方体乙的密度:
ρ乙===0.75×103kg/m3;
③设乙变化后的总质量与甲的质量相等,
ρ乙Sh+ρ乙(V乙﹣Sh)=m乙﹣﹣﹣﹣﹣﹣①
ρ水Sh+ρ乙(V乙﹣Sh)=m甲﹣﹣﹣﹣﹣﹣﹣②
由②﹣①可得:
h===0.12m,
正方体乙的边长:
L乙===0.2m,
因h<L乙,
所以,假设成立。
答:①正方体甲的质量为6.3kg;
②正方体乙的密度为0.75×103kg/m3;
③可能,h=0.12m。
四.密度公式的应用(共20小题)
9.【解答】解:(1)设长方体A的底面边长为a,高为hA,长方体B的底面边长为b,高为hB,a>b且hA>hB,
切去之后SA′=SB′,则切去之后的体积关系为:VA′=SA′hA>VB′=SB′hB,
由于剩余质量mA′=mB′,则长方体A、B的密度:,,因VA′>VB′,所以ρA<ρB;
(2)设切去之后长方体A的宽度为a′,长方体B的宽度为b′,则有:SA′=aa′=SB′=bb′﹣﹣﹣①
由上式得:﹣﹣﹣﹣②
则A的质量为:mA=ρAVA=﹣﹣﹣③
B的质量为:mB=ρBVB=﹣﹣﹣④
③④相比:﹣﹣﹣⑤
联立②⑤两式可得:,所以mA>mB,综上分析可知B正确。
故选:B。
10.【解答】解:V=SH,S甲>S乙,所以△V甲>△V乙。
m甲全部<m乙全部,所以m甲一部分<m乙全部,△m甲<△m乙。
故选:A。
11.【解答】解:(1)因水平面上物体的压力和自身的重力相等,
所以,均匀圆柱体甲对水平地面的压力和自身的重力相等,
因盛有液体乙的薄壁薄底圆柱形容器,
所以,由F=pS=ρghS=ρVg=mg可知,液体乙对容器底部的压力等于液体乙的重力,
又因甲对地面的压力等于液体乙对容器底部的压力,
所以,由F=G=mg可知,圆柱体甲和液体乙的质量相等,
由图可知,甲的体积大于乙的体积,
所以,由ρ=可得,ρ甲<ρ乙,故AB错误;
(2)因圆柱体甲和液体乙的质量相等,
所以,由m=ρV=ρSh得:ρ甲S甲h甲=ρ乙S乙h乙,
由图可知,h甲>h乙,则ρ甲S甲<ρ乙S乙,
现沿水平方向截取部分圆柱体甲并从容器内抽取部分液体乙,使得它们剩余部分的高度或深度均为h,
则剩余部分圆柱体甲和液体乙的质量分别为:
m甲剩=ρ甲S甲h,m乙剩=ρ乙S乙h,
由ρ甲S甲<ρ乙S乙可知,ρ甲S甲h<ρ乙S乙h,即m甲剩<m乙剩,
因圆柱体甲的质量等于截取的质量加上剩余部分的质量,乙液体的质量等于抽取部分的质量加上剩余部分的质量,
所以,m甲+m甲剩=m乙+m乙剩,即m甲>m乙,故C正确、D错误。
故选:C。
12.【解答】解:
(1)因甲、乙的上方沿水平方向切去相同质量后,甲剩余部分质量小于乙剩余部分质量,
所以,m甲切去=m乙切去,m甲剩余<m乙剩余,
由m=m切去+m剩可知,两圆柱体原来的质量关系为m甲<m乙,故AB错误;
(2)因甲剩余部分质量小于乙剩余部分质量,
所以,由m=ρV=ρSh可得,ρ甲S甲h甲剩余<ρ乙S乙h乙剩余,
由图可知,h甲剩余>h乙剩余,则ρ甲S甲<ρ乙S乙,
因甲、乙的上方沿水平方向切去部分的质量相同,
所以,ρ甲S甲h甲切去=ρ乙S乙h乙切去,
由ρ甲S甲<ρ乙S乙可知,h甲切去>h乙切去,
由h=h剩余+h切去可知,两圆柱体原来的高度关系为h甲>h乙,故C错误、D正确。
故选:D。
13.【解答】解:A、已知甲乙容器中液体的质量相等,又因为酒精的密度小于水的密度,因此体积多的液体为酒精,故甲为水,乙为酒精;故A错误;
B、a、b两点水平面以上的液体体积相等,因为酒精的密度小于水的密度,则根据m=ρV可知:a、b两点水平面以上的容器中水的质量比酒精大,由于容器中分别盛有质量相等的水和酒精,则在a、b两点水平面以下,容器中水的质量比酒精小,故B错误;
CD、a、c两点水平面以下的液体体积相等,因为酒精的密度小于水的密度,则根据m=ρV可知:a、c两点水平面以下的容器中水的质量比酒精大,由于容器中分别盛有质量相等的水和酒精,则在a、c两点水平面以上,容器中水的质量比酒精的小,故C错误,D正确。
故选:D。
14.【解答】解:由图甲和乙都为正方体,h甲>h乙,S甲>S乙,所以V甲>V乙.甲、乙质量相等,由ρ=可得m=ρV,
则ρ甲V甲=ρ乙V乙,
ρ甲h甲S甲=ρ乙h乙S乙,
因为h甲>h乙,
所以ρ甲S甲<ρ乙S乙,
现沿水平方向切去切去相同的厚度h后,都为△h,切去的质量△m=ρ△V,
△m甲=ρ甲△hS甲,△m乙=ρ乙△hS乙,
则△m甲<△m乙,
剩余部分质量m′=m﹣△m,
甲剩余部分质量M甲'=m甲﹣△m甲,
乙剩余部分质量M乙'=m乙﹣△m乙,
因为△m甲<△m乙,
所以m甲′>m乙′.故B正确,ACD错误。
故选:B。
15.【解答】解:
由图可知,A和B高度相同,切去相同高度后,剩余部分的高度仍保持相同,由A剩余部分的质量大于B剩余部分的质量,可知同比例减小,则切去前两个圆柱体的质量mA>mB;
已知SA<SB,h相同,则VA<VB,
由ρ=可得,ρA>ρB。
故选:D。
16.【解答】解:由图可以看出,甲的边长小于乙的边长,L甲<L乙,截取相同的厚度△h,所以截去部分的体积△V=L2△h,△V甲<△V乙,故D错误;
采用极限法,把甲物体全部切去,乙仍然留下一部分,所以剩余部分的体积V甲<V乙,剩余部分的质量m甲<m乙,则切去部分的质量△m甲>△m乙,故A正确,B、C错误。
故选:A。
17.【解答】解:甲切去部分的质量为:△m甲=ρ甲△h甲S甲;
乙切去部分的质量为:△m乙=ρ乙△h乙S乙;
所以:=;
甲剩余部分的质量为:m剩甲=ρ甲(h甲﹣△h甲)S甲;
乙剩余部分的质量为:m剩乙=ρ乙(h乙﹣△h乙)S乙;
由于甲、乙剩余部分质量相等,所以:ρ甲(h甲﹣△h甲)S甲=ρ乙(h乙﹣△h乙)S乙;
所以:=;
因为h甲>h乙,
①若△h甲=△h乙,则h甲﹣△h甲>h乙﹣△h乙,所以ρ乙S乙>ρ甲S甲,所以△m甲<△m乙;
②若△h甲<△h乙,则h甲﹣△h甲>h乙﹣△h乙,所以ρ乙S乙>ρ甲S甲,所以△m甲<△m乙;
③若△h甲>△h乙:
当=时,即=时,所以=,所以ρ甲△h甲S甲=ρ乙△h乙S乙,所以△m甲=△m乙;
当<时,即<时,所以<,所以ρ甲△h甲S甲>ρ乙△h乙S乙,所以△m甲>△m乙;
当>时,即>时,所以>,所以ρ甲△h甲S甲<ρ乙△h乙S乙,所以△m甲<△m乙;
故答案为:①若△h甲=△h乙,则△m甲<△m乙;
②若△h甲<△h乙,则△m甲<△m乙;
③若△h甲>△h乙,△m甲=△m乙,或△m甲>△m乙,或△m甲<△m乙。
18.【解答】解:当冰块全部熔化成水后,状态变化,但质量不变,则m水=m冰=1kg,
由ρ=得
水的体积:V水===1×10﹣3m3。
已知冰的密度为0.9×103千克/米3,由V=可得,水的体积小于冰的体积
故答案为:1;1×10﹣3;小于。
19.【解答】解:冰的密度为0.9×103kg/m3,表示1m3冰的质量为0.9×103kg;
水凝固成冰后,状态发生改变,但所含物质的多少没有变化,所以,冰的质量m冰=m水=0.9kg,
由ρ=可得,
冰的体积:V冰===1×10﹣3m3。
故答案为:0.9×103;0.9;1×10﹣3m3。
20.【解答】解:(1)观察图象可知,当体积为0时质量是40g,也就是烧杯中什么也没有时,烧杯的质量为m杯=40g;
(2)由图象中横轴表示物质的体积,纵轴表示物质的质量可知,当液体体积为20cm3时,其质量m=56g﹣40g=16g。
则液体密度ρ===0.8g/cm3=0.8×103kg/m3;
(3)由图象可知,当液体体积为V′=60cm3时,质量m′=ρV′=0.8g/cm3×60cm3=48g,
则m=m杯+m′=40g+48g=88g。
故答案为:40;0.8×103;88。
21.【解答】解:
由ρ=可得甲容器内水的质量:m甲=ρ水V水=ρ水S甲h甲=ρ水×9S×4h=36ρ水Sh﹣﹣﹣﹣﹣﹣﹣①,
乙容器内酒精的质量:m乙=ρ酒精V酒精=ρ酒精S乙h乙=ρ酒精×10S×5h=50ρ酒精Sh,
因ρ酒精=0.8ρ水,所以m乙=50ρ酒精Sh=50×0.8ρ水Sh=40ρ水Sh﹣﹣﹣﹣﹣﹣﹣②,
比较可知m甲<m乙,即原来水的质量较小;
当从两容器中分别加入或抽出相同深度△h的水和酒精时,这些水和酒精的质量分别为:
△m甲=ρ水△V水=ρ水S甲△h=ρ水×9S×△h=9ρ水S△h﹣﹣﹣﹣﹣﹣③,
△m乙=ρ酒精△V酒精=ρ酒精S乙△h=ρ酒精×10S×△h=10ρ酒精S△h=10×0.8ρ水S△h=8ρ水S△h﹣﹣﹣﹣﹣﹣﹣④,
比较可知△m甲>△m乙,即加入或抽出相同深度△h的水的质量更大,
而原来水的质量较小,且抽出相同深度△h的水的质量更大,所以抽出相同深度△h的水后,甲容器中剩余水的质量更小,则采取该方法不能使两容器内水和酒精的质量相等,故应该向容器中加入深度△h的水和酒精,
则此时甲中水的质量为:
m甲′=m甲+△m甲=36ρ水Sh+9ρ水S△h=ρ水S(36h+9△h),
此时乙中酒精的质量为:
m乙′=m乙+△m乙=40ρ水Sh+8ρ水S△h=ρ水S(40h+8△h),
因此时两容器内液体的质量相等,则
ρ水S(36h+9△h)=ρ水S(40h+8△h),
解得△h=4h,
由此可知,为了使甲、乙两容器内水和酒精的质量相等,应向容器中加入深度均为4h的水和酒精。
故答案为:向容器中加入;4h。
22.【解答】解:①由ρ=可得,
甲的质量为:m甲=ρ甲V甲=8×103kg/m3×10﹣3m3=8kg;
②乙的密度为:ρ乙===0.5×103kg/m3,
③若沿水平方向分别在两个正方体的上部各截下相同的厚度d,
则截下部分的质量分别为:
△m甲=ρ甲△V甲=ρ甲S甲d,
△m乙=ρ乙△V乙=ρ乙S乙d,
将乙截下的部分叠放在甲剩下部分的上方,总质量为:
m1=m甲﹣△m甲+△m乙=8kg﹣ρ甲S甲d+ρ乙S乙d=8kg﹣8×103kg/m3×0.1m×0.1m×d+0.5×103kg/m3×0.2m×0.2m×d=(8﹣60d)kg,
将甲截下的部分叠放在乙剩下部分的上方,总质量为:
m2=m乙﹣△m乙+△m甲=4kg﹣ρ乙S乙d+ρ甲S甲d=4kg﹣0.5×103kg/m3×0.2m×0.2m×d+8×103kg/m3×0.1m×0.1m×d=(4+60d)kg,
若要使m1与m2的比值为0.5,即(8﹣60d)kg:(4+60d)kg=0.5,
解得d=m≈0.067m,
因为0.067m<0.1m,
所以存在。
答:①正方体甲的质量为8kg;
②正方体乙的密度为0.5×103kg/m3;
③通过计算可知否存在满足要求的厚度d为0.067m。
23.【解答】解:(1)圆柱形容器甲中水的体积:
V水=Sh=1×10﹣2m×0.1m2=1×10﹣3m3,
由ρ=得,容器甲中水的质量:
m水=ρ水V水=1000kg/m3×1×10﹣3m3=1kg。
(2)由题意知,圆柱形容器乙酒精的质量m酒=m水=1kg,
由ρ=得,容器乙中酒精的体积:
V酒===1.25×10﹣3m3。
(3)铝块的质量m铝=2700g=2.7kg,
由ρ=得,铝块的体积:
V铝===1×10﹣3m3,
将铝块浸没在酒精中时的总体积:
V酒和铝=V酒+V铝=1×10﹣3m3+1.25×10﹣3m3=2.25×10﹣3m3,
因为冰块全部熔化变成水时两个容器中液面一样高,
所以冰块全部熔化变成水时的总体积V水′=V酒和铝=2.25×10﹣3m3,
则增加的水的体积:
△V水=V水′﹣V水=2.25×10﹣3m3﹣1×10﹣3m3=1.25×10﹣3m3,
由ρ=得,增加的水的质量:
△m水=ρ水△V水=1000kg/m3×1.25×10﹣3m3=1.25kg,
因为冰块全部熔化变成水时,状态改变,质量不变,
所以冰块的质量m冰=△m水=1.25kg。
答:①容器甲中水的质量为1kg;
②求乙容器中酒精的体积为1.25×10﹣3m3;
③冰块的质量为1.25kg。
24.【解答】解:(1)由ρ=可得,容器中水的体积:
V水===5×10﹣3m3,
(2)物块A浸没在该容器内水中后,溢出水的体积:V溢=VA=2×10﹣3m3,
m
溢=ρ水V溢=1.0×103kg/m3×2×10﹣3m3=2kg,
m
A=ρAVA=2.9×103kg/m3×2×10﹣3m3=5.8kg,
△m=5.8kg﹣2kg=3.8kg。
答:(1)容器中水的体积为5×10﹣3m3;
(2)整个容器在物块A放入前后的总质量变化量△m为3.8kg。
25.【解答】解:
①A容器中水的体积:
V水=Sh水=2×10﹣2m2×0.1m=2×10﹣3m3,
由ρ=可得,A容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg;
②B容器中酒精的质量:
m酒精=m水=2kg,
则酒精的体积:
V酒精===2.5×10﹣3m3;
③2700克铝块的体积:
V铝===1000cm3=1×10﹣3m3,
因为两个容器中液面一样高,
即V水+V铝=V酒精+V铁,
2×10﹣3m3+1×10﹣3m3=2.5×10﹣3m3+V铁,
所以,铁块的体积:
V铁=5×10﹣4m3,
铁块的质量:
m铁=ρ铁V铁=7.8×103kg/m3×5×10﹣4m3=3.9kg。
答:①A容器中水的质量为2kg。
②B容器中酒精的体积为2.5×10﹣3m3;
③铁块的质量而3.9kg。
26.【解答】解:(1)实心正方体A的体积:VA=(0.1m)3=0.001m3,
由ρ=得,A的质量:
mA=ρAVA=2×103kg/m3×0.001m3=2kg;
(2)实心正方体B的体积:VB=(0.2m)3=0.008m3,
由ρ=得,B的质量:
mB=ρBVB=0.2×103kg/m3×0.008m3=1.6kg;
正方体B的重力:
GB=mBg=1.6kg×9.8N/kg=15.68N;
(3)在正方体A、B上部沿水平方向截去相同高度h,由密度公式得,A、B剩余的质量分别为:
mA′=ρAVA′=ρASA(hA﹣h),mB′=ρBVB′=ρBSB(hB﹣h);
当m′A=m′B时,即ρASA(hA﹣h)=ρBSB(hB﹣h);
代入数据有:2×103kg/m3×0.1m×0.1m×(0.1m﹣h)=0.2×103kg/m3×0.2m×0.2m×(0.2m﹣h)
解得h≈0.03m,
所以当0.1m>h>0.03m时,mA′<mB′;
h=0.03m时,mA′=mB′;
0<h<0.03m时,mA′>mB′。
答:(1)正方体A的质量2kg;
(2)正方体B的重力15.68N;
(3)当0.1m>h>0.03m时,mA′<mB′;
h=0.03m时,mA′=mB′;
0<h<0.03m时,mA′>mB′。
27.【解答】解:
(1)由ρ=可得,甲容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×3×10﹣2m3=30kg;
(2)由题知,甲容器中装满有3×10﹣2m3的水,则甲容器的容积V甲=V水=3×10﹣2m3,
甲、乙的底面积分别为2S、S,容器高度相同,
则乙容器的容积:V乙=V甲=×3×10﹣2m3=1.5×10﹣2m3,
所以最多能注入密度为ρ0的液体的体积:V0=V乙=1.5×10﹣2m3;
(3)物体A浸没于装满水的甲容器中,则甲容器溢出水的体积V溢水=VA=1×10﹣3m3,
溢出水的质量:m溢水=ρ水V溢水=1×103kg/m3×1×10﹣3m3=1kg;
物体B浸没于装满密度为ρ0液体的乙容器中,则乙容器溢出液体的体积V溢0=VB=2×10﹣3m3,
溢出另一种液体的质量:m溢0=ρ0V溢0=ρ0×2×10﹣3m3;
由题知,乙容器中溢出液体的质量是甲容器中溢出水质量的3倍,
即:m溢0=3m溢水,
所以,ρ0×2×10﹣3m3=3×1kg=3kg,
解得:ρ0=1.5×103kg/m3。
答:(1)甲容器中的水的质量为30kg;
(2)往乙容器中注入密度为ρ0的液体,则最多能注入的体积为1.5×10﹣2m3;
(3)密度ρ0的大小为1.5×103kg/m3。
28.【解答】解:
(1)由ρ=得瓶内水的体积:
V1===4×10﹣4m3=400cm3;
(2)石块总体积:
V2=V﹣V1=500cm3﹣400cm3=100cm3;
(3)由ρ=得石块的质量:
m石=ρ石V2=2.6g/cm3×100cm3=260g=0.26kg,
乌鸦投入石块后,瓶子、石块和水的总质量:
m=m水+m瓶+m石=0.4kg+0.5kg+0.26kg=1.16kg=1160g。
答:(1)瓶中水的体积为400cm3;
(2)乌鸦投入瓶子中的石块的体积为100cm3;
(3)乌鸦投入石块后,瓶子、石块和水的总质量为1160g。
五.固体密度的测量(共1小题)
29.【解答】解:(1)测量物体质量的实验仪器是天平;
(2)标尺的分度值为0.2g,物体的质量m=50g+3.4g=53.4g;
(3)量筒的分度值为4cm3,物体和水的总体积为60cm3,物块的体积为V=60cm3﹣40cm3=20cm3;
(4)物块的密度ρ===2.67g/cm3=2.67×103kg/m3。
故答案为:天平;53.4;20;2.67×103。
六.液体密度的测量(共1小题)
30.【解答】解:先测空烧杯质量,将液体倒入烧杯测出液体烧杯总质量,再将液体倒入量筒测体积,这种做法因烧杯壁粘液体,测出的体积偏小,算出的密度偏大。因此测盐水等液体密度的实验步骤安排最合理的是:
①在烧杯中装入适量盐水,测出它们的总质量,
②将烧杯中一部分盐水倒入量筒中,
③测出量筒中盐水的体积,
④测出烧杯和剩余盐水的质量,
⑥根据实验数据计算盐水的密度。
故选:A。
七.空心、混合物质的密度计算(共3小题)
31.【解答】解:若二球都是实心的,质量相等,根据密度公式变形可知:
铝球体积V铝=,铜球体积V铜=,
∵ρ铝<ρ铜,
∴V铝>V铜,
又因为二球的体积相等,所以铜球一定是空心的,铝球可能是实心,也可能是空心。
故选:C。
32.【解答】解:(1)体积之比为:
===,
由ρ=可得质量之比为:
===;
(2)当质量相等时,设质量都为m,
由ρ=得两金属的体积分别为:
V1=、V2=,
两金属的总体积为:
V=V1+V2=+=,
这种合金的密度为:
ρ==。
故答案为:1:4;。
33.【解答】解:(1)根据ρ=可得,铁球中铁的体积:
V1===20cm3<40cm3。
所以,这只铁球是空心的;
(2)空心部分的体积:
V空=V﹣V1=40cm3﹣20cm3=20cm3;
答:(1)计算可知,这只铁球是空心的;
(2)空心部分的体积为20cm3。
八.探究密度特性的实验(共6小题)
34.【解答】解:
①在“测物质的密度”和“探究物质质量与体积的关系”两个实验中需测量的物理量都是:质量与体积,故①正确;
②在这两个实验中,都需用天平测出物体的质量,并用量筒根据排水法测出物体的体积,测量的工具相同,故②正确;
③探究物质质量与体积的关系是为了探究其规律性,应进行多次实验,所以,需要用不同体积的物体进行多次测量;
在“测定物质的密度”的实验中,为了减小实验误差,应进行多次实验,故两个实验中都需要进行多次测量,但多次测量的目的不同;故③正确;
故选:D。
35.【解答】解:(1)“探究物质质量与体积的关系”实验目的是:在物质一定时,探究物体的质量和体积的关系;需要测量物体的质量和体积;
“测定物质的密度”实验目的是:测量物体的密度;需要测量物体的质量和体积,根据密度公式求出物体的密度;
所以两个实验的实验目的不同,需要测量的物理量是相同的;
(2)为了研究质量与体积的关系是否与物质的种类有关,所以在研究了水的质量与体积关系后,还需要用其它液体进行多次实验,这样才能得到普遍性的规律。
故答案为:相同;不同;不同种类的物质;得到普遍性的科学结论。
36.【解答】解:
因“探究物质的质量与体积的关系”,需测量的物理量是质量与体积;则用天平测出液体的质量,并用量筒测出液体的体积;
为了探究其规律性,应进行多次实验,所以,需要改变这种液体的体积进行多次测量;
同时为了进一步研究物质的这一特性与物质的种类是否有关,应需要选用不同种类的物质重复进行实验;
测物质密度实验,用一种物质,进行多次实验,目的是多次测量求平均值,来减小误差。
故答案为:质量;体积;体积;不同;使实验结论具有普遍性;一;多次;求平均值减小误差。
37.【解答】解:(1)根据表一中的数据可知,材料相同,质量和体积都按相同的倍数增大,因此可得出的结论:同种物质组成的物体,质量与体积成正比。
(2)同样的维纳斯塑像,一个是玻璃制品,一个是石膏制品,说明是不同物质,因此乙同学的假设应为相同体积、不同物质的质量不同。
因为假设是相同体积、不同物质的质量不同,故就表二所列的实验数据中,4、5或6、7两组实验数据。
(3)a、分析比较1、2、3可知,同种物质,质量与体积的比值相同。
b、分析比较4、5、6可知,不同物质,质量与体积的比值不同。
故答案为:
(1)同种物质组成的物体,质量与体积成正比。
(2)相同体积,物体的质量与物质种类有关;4、5、6、7。
(3)同种物质,质量与体积的比值相同;不同物质,质量与体积的比值不同。
38.【解答】解:(1)分析表一或表二或表三中物质的质量与体积变化的倍数关系会发现,同种物质,质量与体积的比值是相同,可得出的初步结论是:同种物质,质量与体积成正比;
(2)进一步综合分析比较表一或表二或表三的数据及相关条件,小静认为:同种物质,质量与体积的比值是一个不变的值;但不同物质这个比值不同。小芳认为:同种物质,体积与质量的比值是一个不变的值,但不同物质这个比值不同,两种说法,是同种性质的不同表述形式,故小芳和小静的结论都是正确的。
用手紧压海绵,海绵变密,发现海绵的质量不变、体积变小,质量与体积之比越大,海绵越疏时体积与质量之比越大,在上述两个比值中,质量与体积的比值更能直观合理地反映物质的紧密程度。
故答案为:(1)同种物质,质量与体积成正比;(2)正确;正确;质量与体积;体积与质量;质量与体积。
39.【解答】解:(1)因“探究物质的质量与体积的关系”,为了探究其规律性,应进行多次实验,所以,需要改变这种液体的体积进行多次测量;同时为了进一步研究物质的这一特性与物质的种类是否有关,应需要选用其它种类的液体重复进行实验。
(2)①有关表格内的材料是相同的,故对比同表格内的三组数据,其材料相同,质量和体积都按相同的倍数增大;可得结论:同种物质,质量与体积成正比。
②在研究“体积不同的不同物质,质量一般是不同的”这个猜想是否正确时,应该控制不同种类物质的体积相同,从而比较体积相同的不同物质的质量的关系,得出结论,所以符合条件的数据是实验序号3、9或4与7或5、6、8。
③综合分析比较表中的数据及相关条件,不难看出同种物质,质量与体积的比值是相同的;不同物质,质量与体积的比值是不同的。
故答案为:(1)其它种类的液体;多次。
(2)①同一物质,质量与体积成正比。
②3、9或4与7或5、6、8。
③a.同种物质,质量与体积的比值是相同的;
b.不种物质,质量与体积的比值是不同的。
九.固体的密度测量实验(共1小题)
40.【解答】解:(1)在使用已经调节好的天平,按规范的操作来称量矿石的质量时,通过增减砝码后指针在分读盘中线右边一点,说明右侧砝码的质量多一点,但相差已很少,故此时应从右盘中取下小砝码,同时向右移动游码以达到使天平平衡的目的。
(2)矿石从烧杯中取出后,补充的水的体积就是矿石的体积,而补充的水的体积又是量筒中减少的水的体积,因此,矿石的体积为:200ml﹣130ml=70ml=70cm3;
(3)矿石的密度ρ===2.5g/cm3;
在测量矿石体积的过程中,矿石从烧杯中取出,必然出带出一定的水,从而使补充的水量增加,也就是测量的矿石体积会偏大。质量不变,体积偏大,最终的密度就会偏小。
故答案为:(1)取下最小砝码,移动游码;(2)70;(3)2.5×103;
偏小。
TOC
\o
"1-1"
\h
\u
一.密度及其特性(共2小题)
1
二.密度的大小比较(共2小题)
2
三.密度的计算(共4小题)
2
四.密度公式的应用(共20小题)
3
五.固体密度的测量(共1小题)
10
六.液体密度的测量(共1小题)
10
七.空心、混合物质的密度计算(共3小题)
10
八.探究密度特性的实验(共6小题)
11
九.固体的密度测量实验(共1小题)
13
参考答案及解析
15
目录
15
一.密度及其特性(共2小题)
15
二.密度的大小比较(共2小题)
15
三.密度的计算(共4小题)
16
四.密度公式的应用(共20小题)
18
五.固体密度的测量(共1小题)
29
六.液体密度的测量(共1小题)
29
七.空心、混合物质的密度计算(共3小题)
29
八.探究密度特性的实验(共6小题)
31
九.固体的密度测量实验(共1小题)
33
一.密度及其特性(共2小题)
1.小明同学阅读下表后,得出了一些结论,其中正确的是( )
一些物质的密度/Kg?m﹣3
水
1.0×103
水银
13.6×103
冰
0.9×103
松木
0.5×103
煤油
0.8×103
铜
8.9×103
酒精
0.8×103
铅
11.3×103
A.不同的物质,密度一定不同
B.固体的密度都比液体的大
C.质量相等的实心铜块和实心铅块,铜块的体积比铅块的体积小
D.同种物质在不同状态下,其密度不同
2.如图所示是某实验小组的同学用甲、乙两种不同的物质做实验时得到的m﹣V图线。根据图线可判断( )
A.ρ甲<ρ乙<ρ水
B.ρ甲<ρ乙=ρ水
C.ρ甲>ρ乙=ρ水
D.ρ甲>ρ乙>ρ水
二.密度的大小比较(共2小题)
3.如图所示,均质圆柱形固体A和盛有液体的轻质柱形容器B对水平桌面的压力相等。将固体A沿水平方向切去和容器B中抽出相同的任意高度△h,剩余部分固体对桌面的压强、液体对容器底部的压强分别为PA、PB,要使PA与PB的差值始终保持不变。则它们密度的大小关系是( )
A.ρA可能大于ρB
B.ρA一定等于ρB
C.ρA可能等于ρB
D.ρA一定大于ρB
4.两个完全相同的圆柱形容器甲和乙底部相连通,给两容器分别倒入不同质量的同种液体后,将质量相同的两物块浸没在两容器中(无液体溢出),结果发现有部分液体从乙容器流入甲容器,则( )
A.甲容器中的物块的密度大
B.甲、乙容器中的物块的密度一样大
C.乙容器中的物块的密度大
D.条件不足,无法判断
三.密度的计算(共4小题)
5.某空瓶的质量为0.1千克,在瓶内装满水,测得瓶和水的总质量0.7千克,将质量为0.5千克的金属块浸没在瓶内水中,等停止溢水后再次测得瓶、金属块和剩余水的总质量1.1千克。求:
(1)瓶的容积V容。
(2)溢出水的质量m溢。
(3)金属块的密度ρ金属。
6.一个空瓶的质量为m0,装满某种液体后瓶和液体的总质量是m1.若在该空瓶中先放一些金属颗粒,使瓶和金属颗粒的总质量为m2,然后往瓶里装这种液体直至充满整瓶,用天平测得这时瓶、金属颗粒和液体的总质量为m3,这种液体的密度为ρ液,则瓶里金属颗粒的密度为多少?(请用题目中给出的字母表示,并保留公式推导过程)
7.底面积为1×10﹣2米2薄壁轻质圆柱形容器A(容器足够高)放置于水平地面上,里面盛有0.2米深的水,如图所示。将另一质量为6千克、底面积为5×10﹣3米2的实心金属圆柱体B竖直放入容器A中,待水静止后,圆柱体B上表面露出水面高度为0.1米。
求:(1)容器中水的质量。
(2)金属圆柱体B的密度。
8.如图所示,正方体甲的体积为10﹣3米3,密度为6.3×103千克/米3,正方体乙的体积为8×10﹣3米3,质量为6千克。求:
①正方体甲的质量m甲;
②正方体乙的密度ρ乙;
③若沿正方体乙的上表面挖去一底面积为0.01米2、高为h的长方体,并在挖去部分中倒满水,是否可能使乙变化后的总质量与甲的质量相等?若可能,请计算h;若不可能,请简要说明理由。
四.密度公式的应用(共20小题)
9.如图所示,底面积为正方形的实心长方体A和B放置在水平地面上。若沿竖直方向将A、B两长方体截去一部分,使长方体A、B剩余的面积相等,剩余部分质量m′A等于m′B。则关于长方体A、B的密度ρA、ρB,原来的质量mA、mB的大小关系,下列说法正确的是( )
A.ρA<ρB,mA<mB
B.ρA<ρB,mA>mB
C.ρA>ρB,mA<mB
D.ρA>ρB,mA>mB
10.如图所示,底面积不同的A、B两圆柱体容器分别盛有甲、乙两种液体,已知液体质量m甲<m乙。若在两容器中分别抽出相同高度的液体,则抽出液体的质量△m甲、△m乙和液体的体积△V甲、△V乙的关系是( )
A.△m甲<△m乙,△V甲>△V乙
B.△m甲<△m乙,△V甲<△V乙
C.△m甲>△m乙,△V甲>△V乙
D.△m甲>△m乙,△V甲<△V乙
11.如图所示,均匀圆柱体甲和盛有液体乙的薄壁薄底圆柱形容器置于水平地面,圆柱体和容器的高度相等但底面积不同,甲对地面的压力等于液体乙对容器底部的压力。现沿水平方向截取部分圆柱体甲并从容器内抽取部分液体乙,使得它们剩余部分的高度或深度均为h,则甲、乙的密度ρ以及它们截取或抽取部分质量m的关系是( )
A.ρ甲>ρ乙;m甲>m乙
B.ρ甲>ρ乙;m甲<m乙
C.ρ甲<ρ乙;m甲>m乙
D.ρ甲<ρ乙;m甲<m乙
12.均匀实心圆柱体甲、乙放置在水平地面上。现在甲、乙的上方沿水平方向切去相同质量后,如图所示。甲剩余部分质量小于乙剩余部分质量。则两个圆柱体原来的情况可能是下图中的( )
A.m甲>m乙
h甲>h乙
B.m甲>m乙
h甲=h乙
C.m甲<m乙
h甲<h乙
D.m甲<m乙
h甲>h乙
13.如图所示,在甲、乙两个完全相同的容器中,分别盛有质量相等的水和酒精(已知ρ水>ρ酒),其中a、b两点深度相同,a、c两点距容器底部的距离相同。则下列说法中,正确的是( )
A.甲盛的是酒精,乙盛的是水
B.在a、b两点水平面以下,容器中水的质量比酒精大
C.在a、c两点水平面以上,容器中水的质量比酒精大
D.在a、c两点水平面以下,容器中水的质量比酒精大
14.如图所示,材质均匀且质量相等的正方体甲、乙,放在水平地面上,现沿水平方向切去相同的厚度h后,剩余部分的质量分别为M甲'和M乙',以下正确的是( )
A.甲剩余部分质量M甲'等于乙剩余部分质量M乙'
B.甲剩余部分质量M甲'大于乙剩余部分质量M乙'
C.甲剩余部分质量M甲'小于乙剩余部分质量M乙'
D.不能确定
15.如图所示,水平地面上放有两个底面积不同的实心圆柱体A和B,切去相同高度后,
剩余部分的高度仍保持相同,且A剩余部分的质量大于B剩余部分的质量。则切去前两个圆柱体的质量mA、mB和密度ρA、ρB的大小关系是( )
A.mA<mB,ρA<ρB
B.mA<mB,ρA>ρB
C.mA>mB,ρA<ρB
D.mA>mB,ρA>ρB
16.如图所示,甲、乙两个实心均匀正方形的质量相等,若沿竖直方向分别在两个正方体右侧截取相同的厚度,则甲、乙( )
A.剩余部分的质量m甲<m乙
B.剩余部分的体积V甲=V乙
C.截去部分的质量△m甲<△m乙
D.截去部分的体积△V甲=△V乙
17.如图所示,甲、乙(S甲<S乙,h甲>h乙)两个均匀实心圆柱体放在水平地面上。若在它们上部分别水平切去△h甲、△h乙后,甲和乙剩余部分的质量恰好相等。请按样例,根据△h甲和△h乙的大小关系,写出被切去部分的质量△m甲、△m乙的大小关系。
(样例:若△h甲>△h乙,则△m甲可能大于△m乙。)
18.质量为1千克的冰块全部熔化成水,水的质量为
千克,水的体积为
米3。冰的密度为0.9×103千克/米3,则水的体积
冰的体积(选填“大于”、“等于”或“小于”)。
19.冰的密度为0.9×103千克/米3,表示每立方米冰的质量为
千克。质量为0.9千克的水凝结成冰之后,冰的质量为
千克,冰的体积为
米3。
20.某同学在测量某液体的质量和体积的关系的实验中,得到了如图所示图象,其中纵坐标m表示烧杯和液体的总质量,V表示液体的体积,装液体的空烧杯的质量是
克该液体的密度是
千克/米3,图中m的值应为
克。
21.如图所示,甲、乙两薄壁圆柱形容器(容器足够高)放置在水平桌面上,甲容器底面积为9S、乙容器底面积为10S,甲中盛有深度为4h的水,乙中盛有深度为5h的酒精,为了使甲、乙两容器内水和酒精的质量相等,应
(选填“向容器中加入”或“从容器中抽出”)深度均为
的水和酒精。(ρ酒精=0.8×103kg/m3)
22.如图所示,正方体甲的边长为0.1米,体积为10﹣3米?,密度为8×10?千克/米?,正方体乙的边长为0.2米,体积为8×10﹣3米?,质量为4千克。求:
①正方体甲的质量m甲;
②正方体乙的密度ρ乙;
③若沿水平方向分别在两个正方体的上部各截下相同的厚度d,并将乙截下的部分叠放在甲剩下部分的上方,总质量记为m1,将甲截下的部分叠放在乙剩下部分的上方,总质量记为m2,若要使m1与m2的比值为0.5,请问是否存在满足要求的厚度d,若存在请求出d的取值,若不存在请通过计算说明。
23.如图所示,两个完全相同的圆柱形容器甲和乙放在水平面上(容器足够高),分别装有质量相等的水和酒精,容器的底面积为1×10﹣2米2,容器内水的深度为0.1米(已知ρ水=1000kg/m3,ρ铝=2700kg/m3,ρ冰=900kg/m3)求:
①容器甲中水的质量。
②求乙容器中酒精的体积。
③将2700克铝块浸没在酒精中,将一块冰块放入水中,质量未知的冰块全部熔化变成水时,发现两个容器中液面一样高,求冰块的质量。
24.如图所示,轻质柱形容器底面积为2×10﹣2米2,放在水平地面上,容器中盛满水时,水的质量为5千克,求:
(1)容器中水的体积。
(2)将一个体积为2×10﹣3米3、密度为2.9×103千克/米3的实心均匀物块A浸没在容器内水中后,求整个容器在物块A放入前后总质量的变化量△m。
25.如图所示,A、B两个完全相同圆柱形容器放在水平地面上,容器的底面积为2×10﹣2米2.容器A中盛有一定量的水,水面距容器底部0.1米;B容器中盛有的酒精。(ρ酒精=0.8×103千克/米3,ρ铝=2.7×103千克/米3,ρ铁=7.8×103千克/米3)求:
①A容器中水的质量m水。
②如果B容器中酒精的质量等于水的质量,求B容器中酒精的体积V酒。
③将2700克的铝块浸没在水中,质量未知的铁块浸没在酒精中,发现两个容器中液体的液面一样高(液体不溢出).求铁块的质量m铁。
26.如图所示,实心正方体A、B的边长分别是0.1米,0.2米,密度分别为ρA=2×103千克/米3,ρB=0.2×103千克/米3,求:
(1)正方体A的质量;
(2)正方体B的重力;
(3)若在正方体A、B上部沿水平方向截去相同高度h,A、B剩余的质量为mA′和mB′,请通过计算比较它们的大小关系及其对应的深度h的取值范围。
27.如图所示,两高度均为h的柱形容器甲、乙放置在水平地面上,已知甲、乙的底面积分别为2S、S.甲容器中装满有3×10﹣2米3的水。
(1)求甲容器中的水的质量;
(2)往乙容器中注入密度为ρ0的液体,则最多能注入的体积为多少。
(3)将体积为1×10﹣3米3的物体A浸没于装满水的甲容器中,将体积为2×10﹣3米3的物体B浸没于装满密度为ρ0液体的乙容器中。已知乙容器中溢出液体的质量是甲容器中溢出水质量的3倍。求密度ρ0的大小。
28.如图所示,一个容积V0=500cm3、质量m=0.5kg的瓶子里装有水,乌鸦为了喝到瓶子里的水,就衔了很多的小石块填到瓶子里,让水面上升到瓶口。若瓶内有质量m=0.4kg的水。求:(水的密度ρ水=1.0×103kg/m3,石块密度ρ石块=2.6×103kg/m3)
(1)瓶中水的体积V1;
(2)乌鸦投入瓶子中的石块的体积V2;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
五.固体密度的测量(共1小题)
29.在“测定物质的密度”实验中,用
测物块的质量时,砝码和游码的示数如图(a)所示,则物块的质量为
克;将物块放入盛有40厘米3水的量筒后,水面位置如图(b)所示,则物块的体积为
厘米3,物块的密度为
千克/米3。
六.液体密度的测量(共1小题)
30.为了测出盐水的密度,某实验小组制定了如下的实验计划:
①在烧杯中装入适量盐水,测出它们的总质量:
②将烧杯中的一部分盐水倒入量筒中:
③测出量筒中盐水的体积:
④测出烧杯和剩余盐水的质量;
⑤测出空烧杯的质量;
⑥根据实验数据计算盐水密度
以上实验步骤安排最合理的是( )
A.①②③④⑥
B.⑤①②③⑥
C.①②④③⑤⑥
D.⑤①②④③⑥
七.空心、混合物质的密度计算(共3小题)
31.用相同质量的铝和铜制成体积相等的球,已知ρ铝=2.7×103kg/m3,ρ铜=8.9×103kg/m3,则下列说法正确的( )
A.铜球是空心的,铝球也一定是空心的
B.铝球一定是实心的
C.铜球不可能是实心的
D.铝球和铜球都是实心的
32.甲、乙两个实心的正方体,它们的边长之比是1:2,密度之比是2:1,则它们的质量之比是
;已知
A、B两种金属密度为ρ1、ρ2,取质量相等的
A、B两种金属制成合金,这种合金的密度为
。
33.一只铁球的体积为40厘米3,质量为156克,铁的密度为7.8g/cm3。
(1)问:这只铁球是否空心?请计算作答
(2)若这只铁球是空心的,求空心部分的体积V空。
八.探究密度特性的实验(共6小题)
34.某同学比较“测物质密度”和“探究物质质量与体积关系”两个实验后,认为
①所测的物理量相同
②测量的工具相同③需多次测量的目的不同。他的判断正确的是( )
A.①②
B.②和③
C.①和③
D.①、②和③
35.“探究物质质量与体积关系”实验和“测定铁块的密度”实验相比较:需要测量的物理量
(选填“相同”或“不同”),实验目的
(选填“相同”或“不同”).“探究物质质量与体积关系”实验中,在研究了水的质量与体积关系后,还需要用
进行多次实验,这样做是为
。
36.某同学为了“探究物质的质量与体积的关系”,他先选用某种液体进行实验,用电子天平测出液体的
,并用量筒测出液体的
,为了进行探究,他需要改变这种液体的
进行多次实验。为了进一步研究物质的特性,他还需要选用
(选填“不同”或“相同”)种类的物质进行实验,目的是
;测物质密度实验,用
种物质,进行
实验,目的是
。
37.为了研究物质质量与体积的关系,某兴趣小组同学利用不同的金属块分别进行实验。
(1)甲同学根据“小铁钉和大铁锤的质量不同”的事实,认为“物体的质量可能跟物体的体积有关”。于是就利用仪器测得不同铁块的体积和质量,并将相关数据记录在表一中。则分析比较实验序号1和2和3中质量与体积的倍数关系,可初步得出:
。
表一
实验序号
物质
体积(厘米3)
质量(克)
1
铁
5
39
2
15
117
3
30
234
表二
实验序号
4
5
6
7
8
金属种类
铝
铜
铅
铝
铝
体积(厘米3)
10
10
20
20
30
质量(克)
27
89
226
54
81
(2)乙同学根据“家里同样的维纳斯塑像,玻璃制品和石膏制品的质量不同”的生活经验提出了合理的假设,你认为乙同学的假设应为
。于是,乙同学选用了一些金属块,并测得它们各自的体积和质量,并将相关数据记录在表二中。就表二所列的实验数据中,你认为可用的是
。(选填实验序号)
(3)为了进一步研究物质的某种特性,请你综合分析比较两表中的相关数据,并得出相应的结论:
a
。b
。
38.小静和小芳在“探究物质质量与体积的关系”实验中,分别测出几种物质的质量和体积,测量结果分别记录如表一~表三所示。
表一:塑料颗粒
表二:水
表三:酒精
实验序号
体积/厘米3
质量/克
实验序号
体积/厘米3
质量/克
实验序号
体积/厘米3
质量/克
1
20
26.0
4
35
35.0
7
24
19.2
2
30
39.0
5
44
44.0
8
30
24.0
3
40
52.0
6
50
50.0
9
40
32.0
(1)分析表一或表二或表三中物质的质量与体积变化的倍数关系,可以得出的初步结论是:
。
(2)进一步分析比较三个表中的实验数据,小静认为:同种物质,质量与体积的比值是一个不变的值;但不同物质这个比值不同。小芳认为:同种物质,体积与质量的比值是一个不变的值,但不同物质这个比值不同。你认为小静的观点
,小芳的观点
。(均选填“正确”或“错误”)
为了比较上述两个“比值”的意义,他们找了一块海绵,用手紧压海绵,发现海绵的质量不变、体积变小,说明海绵越密时,
的比值越大,海绵越疏时,
的比值越大。在上述两个比值中,
比值更能直观合理地反映物质的紧密程度。
39.为了“探究物质质量与体积的关系”,小王和小李同学分别进行实验:
(1)小王:探究液体质量与体积的关系,他选用的实验器材有:天平(带砝码)、量筒、烧杯、水和
。实验中,为了得到比较完整的结论,要进行
测量(填“一次”或“多次”)。
(2)小李同学探究固体质量与体积的关系,他选用的实验器材除天平(带砝码)、量筒、烧杯和水外,还选用了不同体积,不同质量的金属块若干。实验时,他分别测得不同金属块的体积和质量,并将相关数据记录在表中。
物质
铁
铜
铅
铝
实验序号
1
2
3
4
5
6
7
8
9
体积/厘米3
5
15
30
10
20
20
10
20
30
质量/克
39
117
234
89
178
226
27
54
81
①分析上表的实验序号l、2与3或4与5或7、8与9的体积及质量变化的倍数关系,可归纳出的初步结论是:
。
⑦分析上表中实验序号
的关系。可归纳出的初步结论是:相同体积的不同物质,它们的质量是不同的。
③请进一步综合分析比较表中的效据,并归纳得出结论。
(a)
。
(b)
。
九.固体的密度测量实验(共1小题)
40.小明在实验室里测量一块形状不规则、体积较大的矿石的密度。
(1)在使用已调节好的托盘天平,按规范的操作来称量矿石的质量时,通过增、减砝码后都不能使天平平衡,指针仍然偏在分度盘中线右边一点,这时应该
。
(2)因矿石体积较大放不进量筒,因此他利用一只烧杯,按图所示方法进行测量,则矿石的体积是
cm3
(3)用托盘天平已测得矿石的质量是175g,则矿石的密度是
千克/米3;从图A到图B的操作引起的密度测量值比真实值
(选填:“偏大”、“偏小”或“不变”)。
参考答案及解析
一.密度及其特性(共2小题)
1.【解答】解:A、表中煤油和酒精的密度均为0.8×103kg?m﹣3,故此选项错误。
B、表中松木是固体,密度小于液体水银的密度,故此选项错误。
C、根据公式V=m/ρ,质量相同时,密度越大体积越小,铜的密度小于铅的密度,故铜的体积大于铅的体积。
D、由表中数据,对于同种物质,水和冰的密度不同。
故选:D。
2.【解答】解:由图示可知:
ρ甲===1.75g/cm3;
ρ乙===1g/cm3=ρ水;
故选:C。
二.密度的大小比较(共2小题)
3.【解答】解:因为A为规则固体,B为轻质柱形容器容器,则A对桌面的压强:pA=ρAghA,B内液体对容器底的压强:pB=ρBghB,
因为A对水平桌面的压力和B对水平桌面的压力相等,而SA<SB,由p=可得,A对水平桌面的压强大于B对容器底的压强;
∴ρAghA>ρBghB
∵hA>hB
∴ρA可能大于、小于或等于ρB,
∵PA与PB的差值始终保持不变,
∴A、B的压强变化量满足△P=△PA﹣△PB=0,即ρAg△h﹣ρBg△h=0,
∴ρA=ρB。
故选:B。
4.【解答】解:发现有部分水从乙容器流入甲容器,说明放入物块后乙容器中水面比甲容器中高;因为容器完全相同,也就是说乙容器中物块排开水的体积大,因为都是浸没在两容器的水中并且水没有溢出容器外,说明乙容器中的体积大;两个物块的质量相同,乙容器中物块的体积大,根据密度的公式ρ=,所以乙容器中物块的密度小,甲容器中物块的密度大。
故选:A。
三.密度的计算(共4小题)
5.【解答】解:
(1)瓶子中装满水后水的质量:m水=0.7kg﹣0.1kg=0.6kg=600g,
由ρ=可得空瓶容积:
V=V水===600cm3;
(2)溢出水的质量:m溢=0.5kg+0.7kg﹣1.1kg=0.1kg=100g,
(3)金属块的体积:
V金=V溢===100cm3,
金属块的质量:m金=0.5kg=500g,
金属块的密度:
ρ===5g/cm3=5×103kg/m3。
答:(1)瓶的容积为600cm3;
(2)溢出水的质量为100g;
(3)金属块的密度5×103kg/m3。
6.【解答】解:空瓶装满液体时液体的质量:
m液=m1﹣m0,
由ρ=可得,空瓶的容积:
V=V液==,
金属粒的质量:
m金=m2﹣m0,
瓶中装了金属粒后再装满液体,此时瓶中液体的质量:
m液'=m3﹣m2,
此时瓶中液体的体积:
V液'==,
则金属粒的体积:
V金=V﹣V'水=﹣=,
金属粒的密度:
ρ金===。
答:瓶里金属颗粒的密度为。
7.【解答】解:(1)容器中水的体积:
V水=S容h=1×10﹣2m2×0.2m=2×10﹣3m3,
由ρ=可得,容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg;
(2)由题知,金属圆柱体放入水中后,露出水面0.1m,设此时水深为h水,
则水的体积为V水=(S容﹣S金)h水,
所以,此时的水深:
h水===0.4m,
则金属圆柱体的高度:
h金=h水+h露=0.4m+0.1m=0.5m,
金属圆柱体的体积:
V金=S金h金=5×10﹣3m2×0.5m=2.5×10﹣3m3,
金属圆柱体B的密度:
ρ金===2.4×103kg/m3。
答:(1)容器中水的质量为2kg;
(2)金属圆柱体B的密度为2.4×103kg/m3。
8.【解答】解:①由ρ=可得,正方体甲的质量:
m甲=ρ甲V甲=6.3×103kg/m3×10﹣3m3=6.3kg;
②正方体乙的密度:
ρ乙===0.75×103kg/m3;
③设乙变化后的总质量与甲的质量相等,
ρ乙Sh+ρ乙(V乙﹣Sh)=m乙﹣﹣﹣﹣﹣﹣①
ρ水Sh+ρ乙(V乙﹣Sh)=m甲﹣﹣﹣﹣﹣﹣﹣②
由②﹣①可得:
h===0.12m,
正方体乙的边长:
L乙===0.2m,
因h<L乙,
所以,假设成立。
答:①正方体甲的质量为6.3kg;
②正方体乙的密度为0.75×103kg/m3;
③可能,h=0.12m。
四.密度公式的应用(共20小题)
9.【解答】解:(1)设长方体A的底面边长为a,高为hA,长方体B的底面边长为b,高为hB,a>b且hA>hB,
切去之后SA′=SB′,则切去之后的体积关系为:VA′=SA′hA>VB′=SB′hB,
由于剩余质量mA′=mB′,则长方体A、B的密度:,,因VA′>VB′,所以ρA<ρB;
(2)设切去之后长方体A的宽度为a′,长方体B的宽度为b′,则有:SA′=aa′=SB′=bb′﹣﹣﹣①
由上式得:﹣﹣﹣﹣②
则A的质量为:mA=ρAVA=﹣﹣﹣③
B的质量为:mB=ρBVB=﹣﹣﹣④
③④相比:﹣﹣﹣⑤
联立②⑤两式可得:,所以mA>mB,综上分析可知B正确。
故选:B。
10.【解答】解:V=SH,S甲>S乙,所以△V甲>△V乙。
m甲全部<m乙全部,所以m甲一部分<m乙全部,△m甲<△m乙。
故选:A。
11.【解答】解:(1)因水平面上物体的压力和自身的重力相等,
所以,均匀圆柱体甲对水平地面的压力和自身的重力相等,
因盛有液体乙的薄壁薄底圆柱形容器,
所以,由F=pS=ρghS=ρVg=mg可知,液体乙对容器底部的压力等于液体乙的重力,
又因甲对地面的压力等于液体乙对容器底部的压力,
所以,由F=G=mg可知,圆柱体甲和液体乙的质量相等,
由图可知,甲的体积大于乙的体积,
所以,由ρ=可得,ρ甲<ρ乙,故AB错误;
(2)因圆柱体甲和液体乙的质量相等,
所以,由m=ρV=ρSh得:ρ甲S甲h甲=ρ乙S乙h乙,
由图可知,h甲>h乙,则ρ甲S甲<ρ乙S乙,
现沿水平方向截取部分圆柱体甲并从容器内抽取部分液体乙,使得它们剩余部分的高度或深度均为h,
则剩余部分圆柱体甲和液体乙的质量分别为:
m甲剩=ρ甲S甲h,m乙剩=ρ乙S乙h,
由ρ甲S甲<ρ乙S乙可知,ρ甲S甲h<ρ乙S乙h,即m甲剩<m乙剩,
因圆柱体甲的质量等于截取的质量加上剩余部分的质量,乙液体的质量等于抽取部分的质量加上剩余部分的质量,
所以,m甲+m甲剩=m乙+m乙剩,即m甲>m乙,故C正确、D错误。
故选:C。
12.【解答】解:
(1)因甲、乙的上方沿水平方向切去相同质量后,甲剩余部分质量小于乙剩余部分质量,
所以,m甲切去=m乙切去,m甲剩余<m乙剩余,
由m=m切去+m剩可知,两圆柱体原来的质量关系为m甲<m乙,故AB错误;
(2)因甲剩余部分质量小于乙剩余部分质量,
所以,由m=ρV=ρSh可得,ρ甲S甲h甲剩余<ρ乙S乙h乙剩余,
由图可知,h甲剩余>h乙剩余,则ρ甲S甲<ρ乙S乙,
因甲、乙的上方沿水平方向切去部分的质量相同,
所以,ρ甲S甲h甲切去=ρ乙S乙h乙切去,
由ρ甲S甲<ρ乙S乙可知,h甲切去>h乙切去,
由h=h剩余+h切去可知,两圆柱体原来的高度关系为h甲>h乙,故C错误、D正确。
故选:D。
13.【解答】解:A、已知甲乙容器中液体的质量相等,又因为酒精的密度小于水的密度,因此体积多的液体为酒精,故甲为水,乙为酒精;故A错误;
B、a、b两点水平面以上的液体体积相等,因为酒精的密度小于水的密度,则根据m=ρV可知:a、b两点水平面以上的容器中水的质量比酒精大,由于容器中分别盛有质量相等的水和酒精,则在a、b两点水平面以下,容器中水的质量比酒精小,故B错误;
CD、a、c两点水平面以下的液体体积相等,因为酒精的密度小于水的密度,则根据m=ρV可知:a、c两点水平面以下的容器中水的质量比酒精大,由于容器中分别盛有质量相等的水和酒精,则在a、c两点水平面以上,容器中水的质量比酒精的小,故C错误,D正确。
故选:D。
14.【解答】解:由图甲和乙都为正方体,h甲>h乙,S甲>S乙,所以V甲>V乙.甲、乙质量相等,由ρ=可得m=ρV,
则ρ甲V甲=ρ乙V乙,
ρ甲h甲S甲=ρ乙h乙S乙,
因为h甲>h乙,
所以ρ甲S甲<ρ乙S乙,
现沿水平方向切去切去相同的厚度h后,都为△h,切去的质量△m=ρ△V,
△m甲=ρ甲△hS甲,△m乙=ρ乙△hS乙,
则△m甲<△m乙,
剩余部分质量m′=m﹣△m,
甲剩余部分质量M甲'=m甲﹣△m甲,
乙剩余部分质量M乙'=m乙﹣△m乙,
因为△m甲<△m乙,
所以m甲′>m乙′.故B正确,ACD错误。
故选:B。
15.【解答】解:
由图可知,A和B高度相同,切去相同高度后,剩余部分的高度仍保持相同,由A剩余部分的质量大于B剩余部分的质量,可知同比例减小,则切去前两个圆柱体的质量mA>mB;
已知SA<SB,h相同,则VA<VB,
由ρ=可得,ρA>ρB。
故选:D。
16.【解答】解:由图可以看出,甲的边长小于乙的边长,L甲<L乙,截取相同的厚度△h,所以截去部分的体积△V=L2△h,△V甲<△V乙,故D错误;
采用极限法,把甲物体全部切去,乙仍然留下一部分,所以剩余部分的体积V甲<V乙,剩余部分的质量m甲<m乙,则切去部分的质量△m甲>△m乙,故A正确,B、C错误。
故选:A。
17.【解答】解:甲切去部分的质量为:△m甲=ρ甲△h甲S甲;
乙切去部分的质量为:△m乙=ρ乙△h乙S乙;
所以:=;
甲剩余部分的质量为:m剩甲=ρ甲(h甲﹣△h甲)S甲;
乙剩余部分的质量为:m剩乙=ρ乙(h乙﹣△h乙)S乙;
由于甲、乙剩余部分质量相等,所以:ρ甲(h甲﹣△h甲)S甲=ρ乙(h乙﹣△h乙)S乙;
所以:=;
因为h甲>h乙,
①若△h甲=△h乙,则h甲﹣△h甲>h乙﹣△h乙,所以ρ乙S乙>ρ甲S甲,所以△m甲<△m乙;
②若△h甲<△h乙,则h甲﹣△h甲>h乙﹣△h乙,所以ρ乙S乙>ρ甲S甲,所以△m甲<△m乙;
③若△h甲>△h乙:
当=时,即=时,所以=,所以ρ甲△h甲S甲=ρ乙△h乙S乙,所以△m甲=△m乙;
当<时,即<时,所以<,所以ρ甲△h甲S甲>ρ乙△h乙S乙,所以△m甲>△m乙;
当>时,即>时,所以>,所以ρ甲△h甲S甲<ρ乙△h乙S乙,所以△m甲<△m乙;
故答案为:①若△h甲=△h乙,则△m甲<△m乙;
②若△h甲<△h乙,则△m甲<△m乙;
③若△h甲>△h乙,△m甲=△m乙,或△m甲>△m乙,或△m甲<△m乙。
18.【解答】解:当冰块全部熔化成水后,状态变化,但质量不变,则m水=m冰=1kg,
由ρ=得
水的体积:V水===1×10﹣3m3。
已知冰的密度为0.9×103千克/米3,由V=可得,水的体积小于冰的体积
故答案为:1;1×10﹣3;小于。
19.【解答】解:冰的密度为0.9×103kg/m3,表示1m3冰的质量为0.9×103kg;
水凝固成冰后,状态发生改变,但所含物质的多少没有变化,所以,冰的质量m冰=m水=0.9kg,
由ρ=可得,
冰的体积:V冰===1×10﹣3m3。
故答案为:0.9×103;0.9;1×10﹣3m3。
20.【解答】解:(1)观察图象可知,当体积为0时质量是40g,也就是烧杯中什么也没有时,烧杯的质量为m杯=40g;
(2)由图象中横轴表示物质的体积,纵轴表示物质的质量可知,当液体体积为20cm3时,其质量m=56g﹣40g=16g。
则液体密度ρ===0.8g/cm3=0.8×103kg/m3;
(3)由图象可知,当液体体积为V′=60cm3时,质量m′=ρV′=0.8g/cm3×60cm3=48g,
则m=m杯+m′=40g+48g=88g。
故答案为:40;0.8×103;88。
21.【解答】解:
由ρ=可得甲容器内水的质量:m甲=ρ水V水=ρ水S甲h甲=ρ水×9S×4h=36ρ水Sh﹣﹣﹣﹣﹣﹣﹣①,
乙容器内酒精的质量:m乙=ρ酒精V酒精=ρ酒精S乙h乙=ρ酒精×10S×5h=50ρ酒精Sh,
因ρ酒精=0.8ρ水,所以m乙=50ρ酒精Sh=50×0.8ρ水Sh=40ρ水Sh﹣﹣﹣﹣﹣﹣﹣②,
比较可知m甲<m乙,即原来水的质量较小;
当从两容器中分别加入或抽出相同深度△h的水和酒精时,这些水和酒精的质量分别为:
△m甲=ρ水△V水=ρ水S甲△h=ρ水×9S×△h=9ρ水S△h﹣﹣﹣﹣﹣﹣③,
△m乙=ρ酒精△V酒精=ρ酒精S乙△h=ρ酒精×10S×△h=10ρ酒精S△h=10×0.8ρ水S△h=8ρ水S△h﹣﹣﹣﹣﹣﹣﹣④,
比较可知△m甲>△m乙,即加入或抽出相同深度△h的水的质量更大,
而原来水的质量较小,且抽出相同深度△h的水的质量更大,所以抽出相同深度△h的水后,甲容器中剩余水的质量更小,则采取该方法不能使两容器内水和酒精的质量相等,故应该向容器中加入深度△h的水和酒精,
则此时甲中水的质量为:
m甲′=m甲+△m甲=36ρ水Sh+9ρ水S△h=ρ水S(36h+9△h),
此时乙中酒精的质量为:
m乙′=m乙+△m乙=40ρ水Sh+8ρ水S△h=ρ水S(40h+8△h),
因此时两容器内液体的质量相等,则
ρ水S(36h+9△h)=ρ水S(40h+8△h),
解得△h=4h,
由此可知,为了使甲、乙两容器内水和酒精的质量相等,应向容器中加入深度均为4h的水和酒精。
故答案为:向容器中加入;4h。
22.【解答】解:①由ρ=可得,
甲的质量为:m甲=ρ甲V甲=8×103kg/m3×10﹣3m3=8kg;
②乙的密度为:ρ乙===0.5×103kg/m3,
③若沿水平方向分别在两个正方体的上部各截下相同的厚度d,
则截下部分的质量分别为:
△m甲=ρ甲△V甲=ρ甲S甲d,
△m乙=ρ乙△V乙=ρ乙S乙d,
将乙截下的部分叠放在甲剩下部分的上方,总质量为:
m1=m甲﹣△m甲+△m乙=8kg﹣ρ甲S甲d+ρ乙S乙d=8kg﹣8×103kg/m3×0.1m×0.1m×d+0.5×103kg/m3×0.2m×0.2m×d=(8﹣60d)kg,
将甲截下的部分叠放在乙剩下部分的上方,总质量为:
m2=m乙﹣△m乙+△m甲=4kg﹣ρ乙S乙d+ρ甲S甲d=4kg﹣0.5×103kg/m3×0.2m×0.2m×d+8×103kg/m3×0.1m×0.1m×d=(4+60d)kg,
若要使m1与m2的比值为0.5,即(8﹣60d)kg:(4+60d)kg=0.5,
解得d=m≈0.067m,
因为0.067m<0.1m,
所以存在。
答:①正方体甲的质量为8kg;
②正方体乙的密度为0.5×103kg/m3;
③通过计算可知否存在满足要求的厚度d为0.067m。
23.【解答】解:(1)圆柱形容器甲中水的体积:
V水=Sh=1×10﹣2m×0.1m2=1×10﹣3m3,
由ρ=得,容器甲中水的质量:
m水=ρ水V水=1000kg/m3×1×10﹣3m3=1kg。
(2)由题意知,圆柱形容器乙酒精的质量m酒=m水=1kg,
由ρ=得,容器乙中酒精的体积:
V酒===1.25×10﹣3m3。
(3)铝块的质量m铝=2700g=2.7kg,
由ρ=得,铝块的体积:
V铝===1×10﹣3m3,
将铝块浸没在酒精中时的总体积:
V酒和铝=V酒+V铝=1×10﹣3m3+1.25×10﹣3m3=2.25×10﹣3m3,
因为冰块全部熔化变成水时两个容器中液面一样高,
所以冰块全部熔化变成水时的总体积V水′=V酒和铝=2.25×10﹣3m3,
则增加的水的体积:
△V水=V水′﹣V水=2.25×10﹣3m3﹣1×10﹣3m3=1.25×10﹣3m3,
由ρ=得,增加的水的质量:
△m水=ρ水△V水=1000kg/m3×1.25×10﹣3m3=1.25kg,
因为冰块全部熔化变成水时,状态改变,质量不变,
所以冰块的质量m冰=△m水=1.25kg。
答:①容器甲中水的质量为1kg;
②求乙容器中酒精的体积为1.25×10﹣3m3;
③冰块的质量为1.25kg。
24.【解答】解:(1)由ρ=可得,容器中水的体积:
V水===5×10﹣3m3,
(2)物块A浸没在该容器内水中后,溢出水的体积:V溢=VA=2×10﹣3m3,
m
溢=ρ水V溢=1.0×103kg/m3×2×10﹣3m3=2kg,
m
A=ρAVA=2.9×103kg/m3×2×10﹣3m3=5.8kg,
△m=5.8kg﹣2kg=3.8kg。
答:(1)容器中水的体积为5×10﹣3m3;
(2)整个容器在物块A放入前后的总质量变化量△m为3.8kg。
25.【解答】解:
①A容器中水的体积:
V水=Sh水=2×10﹣2m2×0.1m=2×10﹣3m3,
由ρ=可得,A容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg;
②B容器中酒精的质量:
m酒精=m水=2kg,
则酒精的体积:
V酒精===2.5×10﹣3m3;
③2700克铝块的体积:
V铝===1000cm3=1×10﹣3m3,
因为两个容器中液面一样高,
即V水+V铝=V酒精+V铁,
2×10﹣3m3+1×10﹣3m3=2.5×10﹣3m3+V铁,
所以,铁块的体积:
V铁=5×10﹣4m3,
铁块的质量:
m铁=ρ铁V铁=7.8×103kg/m3×5×10﹣4m3=3.9kg。
答:①A容器中水的质量为2kg。
②B容器中酒精的体积为2.5×10﹣3m3;
③铁块的质量而3.9kg。
26.【解答】解:(1)实心正方体A的体积:VA=(0.1m)3=0.001m3,
由ρ=得,A的质量:
mA=ρAVA=2×103kg/m3×0.001m3=2kg;
(2)实心正方体B的体积:VB=(0.2m)3=0.008m3,
由ρ=得,B的质量:
mB=ρBVB=0.2×103kg/m3×0.008m3=1.6kg;
正方体B的重力:
GB=mBg=1.6kg×9.8N/kg=15.68N;
(3)在正方体A、B上部沿水平方向截去相同高度h,由密度公式得,A、B剩余的质量分别为:
mA′=ρAVA′=ρASA(hA﹣h),mB′=ρBVB′=ρBSB(hB﹣h);
当m′A=m′B时,即ρASA(hA﹣h)=ρBSB(hB﹣h);
代入数据有:2×103kg/m3×0.1m×0.1m×(0.1m﹣h)=0.2×103kg/m3×0.2m×0.2m×(0.2m﹣h)
解得h≈0.03m,
所以当0.1m>h>0.03m时,mA′<mB′;
h=0.03m时,mA′=mB′;
0<h<0.03m时,mA′>mB′。
答:(1)正方体A的质量2kg;
(2)正方体B的重力15.68N;
(3)当0.1m>h>0.03m时,mA′<mB′;
h=0.03m时,mA′=mB′;
0<h<0.03m时,mA′>mB′。
27.【解答】解:
(1)由ρ=可得,甲容器中水的质量:
m水=ρ水V水=1.0×103kg/m3×3×10﹣2m3=30kg;
(2)由题知,甲容器中装满有3×10﹣2m3的水,则甲容器的容积V甲=V水=3×10﹣2m3,
甲、乙的底面积分别为2S、S,容器高度相同,
则乙容器的容积:V乙=V甲=×3×10﹣2m3=1.5×10﹣2m3,
所以最多能注入密度为ρ0的液体的体积:V0=V乙=1.5×10﹣2m3;
(3)物体A浸没于装满水的甲容器中,则甲容器溢出水的体积V溢水=VA=1×10﹣3m3,
溢出水的质量:m溢水=ρ水V溢水=1×103kg/m3×1×10﹣3m3=1kg;
物体B浸没于装满密度为ρ0液体的乙容器中,则乙容器溢出液体的体积V溢0=VB=2×10﹣3m3,
溢出另一种液体的质量:m溢0=ρ0V溢0=ρ0×2×10﹣3m3;
由题知,乙容器中溢出液体的质量是甲容器中溢出水质量的3倍,
即:m溢0=3m溢水,
所以,ρ0×2×10﹣3m3=3×1kg=3kg,
解得:ρ0=1.5×103kg/m3。
答:(1)甲容器中的水的质量为30kg;
(2)往乙容器中注入密度为ρ0的液体,则最多能注入的体积为1.5×10﹣2m3;
(3)密度ρ0的大小为1.5×103kg/m3。
28.【解答】解:
(1)由ρ=得瓶内水的体积:
V1===4×10﹣4m3=400cm3;
(2)石块总体积:
V2=V﹣V1=500cm3﹣400cm3=100cm3;
(3)由ρ=得石块的质量:
m石=ρ石V2=2.6g/cm3×100cm3=260g=0.26kg,
乌鸦投入石块后,瓶子、石块和水的总质量:
m=m水+m瓶+m石=0.4kg+0.5kg+0.26kg=1.16kg=1160g。
答:(1)瓶中水的体积为400cm3;
(2)乌鸦投入瓶子中的石块的体积为100cm3;
(3)乌鸦投入石块后,瓶子、石块和水的总质量为1160g。
五.固体密度的测量(共1小题)
29.【解答】解:(1)测量物体质量的实验仪器是天平;
(2)标尺的分度值为0.2g,物体的质量m=50g+3.4g=53.4g;
(3)量筒的分度值为4cm3,物体和水的总体积为60cm3,物块的体积为V=60cm3﹣40cm3=20cm3;
(4)物块的密度ρ===2.67g/cm3=2.67×103kg/m3。
故答案为:天平;53.4;20;2.67×103。
六.液体密度的测量(共1小题)
30.【解答】解:先测空烧杯质量,将液体倒入烧杯测出液体烧杯总质量,再将液体倒入量筒测体积,这种做法因烧杯壁粘液体,测出的体积偏小,算出的密度偏大。因此测盐水等液体密度的实验步骤安排最合理的是:
①在烧杯中装入适量盐水,测出它们的总质量,
②将烧杯中一部分盐水倒入量筒中,
③测出量筒中盐水的体积,
④测出烧杯和剩余盐水的质量,
⑥根据实验数据计算盐水的密度。
故选:A。
七.空心、混合物质的密度计算(共3小题)
31.【解答】解:若二球都是实心的,质量相等,根据密度公式变形可知:
铝球体积V铝=,铜球体积V铜=,
∵ρ铝<ρ铜,
∴V铝>V铜,
又因为二球的体积相等,所以铜球一定是空心的,铝球可能是实心,也可能是空心。
故选:C。
32.【解答】解:(1)体积之比为:
===,
由ρ=可得质量之比为:
===;
(2)当质量相等时,设质量都为m,
由ρ=得两金属的体积分别为:
V1=、V2=,
两金属的总体积为:
V=V1+V2=+=,
这种合金的密度为:
ρ==。
故答案为:1:4;。
33.【解答】解:(1)根据ρ=可得,铁球中铁的体积:
V1===20cm3<40cm3。
所以,这只铁球是空心的;
(2)空心部分的体积:
V空=V﹣V1=40cm3﹣20cm3=20cm3;
答:(1)计算可知,这只铁球是空心的;
(2)空心部分的体积为20cm3。
八.探究密度特性的实验(共6小题)
34.【解答】解:
①在“测物质的密度”和“探究物质质量与体积的关系”两个实验中需测量的物理量都是:质量与体积,故①正确;
②在这两个实验中,都需用天平测出物体的质量,并用量筒根据排水法测出物体的体积,测量的工具相同,故②正确;
③探究物质质量与体积的关系是为了探究其规律性,应进行多次实验,所以,需要用不同体积的物体进行多次测量;
在“测定物质的密度”的实验中,为了减小实验误差,应进行多次实验,故两个实验中都需要进行多次测量,但多次测量的目的不同;故③正确;
故选:D。
35.【解答】解:(1)“探究物质质量与体积的关系”实验目的是:在物质一定时,探究物体的质量和体积的关系;需要测量物体的质量和体积;
“测定物质的密度”实验目的是:测量物体的密度;需要测量物体的质量和体积,根据密度公式求出物体的密度;
所以两个实验的实验目的不同,需要测量的物理量是相同的;
(2)为了研究质量与体积的关系是否与物质的种类有关,所以在研究了水的质量与体积关系后,还需要用其它液体进行多次实验,这样才能得到普遍性的规律。
故答案为:相同;不同;不同种类的物质;得到普遍性的科学结论。
36.【解答】解:
因“探究物质的质量与体积的关系”,需测量的物理量是质量与体积;则用天平测出液体的质量,并用量筒测出液体的体积;
为了探究其规律性,应进行多次实验,所以,需要改变这种液体的体积进行多次测量;
同时为了进一步研究物质的这一特性与物质的种类是否有关,应需要选用不同种类的物质重复进行实验;
测物质密度实验,用一种物质,进行多次实验,目的是多次测量求平均值,来减小误差。
故答案为:质量;体积;体积;不同;使实验结论具有普遍性;一;多次;求平均值减小误差。
37.【解答】解:(1)根据表一中的数据可知,材料相同,质量和体积都按相同的倍数增大,因此可得出的结论:同种物质组成的物体,质量与体积成正比。
(2)同样的维纳斯塑像,一个是玻璃制品,一个是石膏制品,说明是不同物质,因此乙同学的假设应为相同体积、不同物质的质量不同。
因为假设是相同体积、不同物质的质量不同,故就表二所列的实验数据中,4、5或6、7两组实验数据。
(3)a、分析比较1、2、3可知,同种物质,质量与体积的比值相同。
b、分析比较4、5、6可知,不同物质,质量与体积的比值不同。
故答案为:
(1)同种物质组成的物体,质量与体积成正比。
(2)相同体积,物体的质量与物质种类有关;4、5、6、7。
(3)同种物质,质量与体积的比值相同;不同物质,质量与体积的比值不同。
38.【解答】解:(1)分析表一或表二或表三中物质的质量与体积变化的倍数关系会发现,同种物质,质量与体积的比值是相同,可得出的初步结论是:同种物质,质量与体积成正比;
(2)进一步综合分析比较表一或表二或表三的数据及相关条件,小静认为:同种物质,质量与体积的比值是一个不变的值;但不同物质这个比值不同。小芳认为:同种物质,体积与质量的比值是一个不变的值,但不同物质这个比值不同,两种说法,是同种性质的不同表述形式,故小芳和小静的结论都是正确的。
用手紧压海绵,海绵变密,发现海绵的质量不变、体积变小,质量与体积之比越大,海绵越疏时体积与质量之比越大,在上述两个比值中,质量与体积的比值更能直观合理地反映物质的紧密程度。
故答案为:(1)同种物质,质量与体积成正比;(2)正确;正确;质量与体积;体积与质量;质量与体积。
39.【解答】解:(1)因“探究物质的质量与体积的关系”,为了探究其规律性,应进行多次实验,所以,需要改变这种液体的体积进行多次测量;同时为了进一步研究物质的这一特性与物质的种类是否有关,应需要选用其它种类的液体重复进行实验。
(2)①有关表格内的材料是相同的,故对比同表格内的三组数据,其材料相同,质量和体积都按相同的倍数增大;可得结论:同种物质,质量与体积成正比。
②在研究“体积不同的不同物质,质量一般是不同的”这个猜想是否正确时,应该控制不同种类物质的体积相同,从而比较体积相同的不同物质的质量的关系,得出结论,所以符合条件的数据是实验序号3、9或4与7或5、6、8。
③综合分析比较表中的数据及相关条件,不难看出同种物质,质量与体积的比值是相同的;不同物质,质量与体积的比值是不同的。
故答案为:(1)其它种类的液体;多次。
(2)①同一物质,质量与体积成正比。
②3、9或4与7或5、6、8。
③a.同种物质,质量与体积的比值是相同的;
b.不种物质,质量与体积的比值是不同的。
九.固体的密度测量实验(共1小题)
40.【解答】解:(1)在使用已经调节好的天平,按规范的操作来称量矿石的质量时,通过增减砝码后指针在分读盘中线右边一点,说明右侧砝码的质量多一点,但相差已很少,故此时应从右盘中取下小砝码,同时向右移动游码以达到使天平平衡的目的。
(2)矿石从烧杯中取出后,补充的水的体积就是矿石的体积,而补充的水的体积又是量筒中减少的水的体积,因此,矿石的体积为:200ml﹣130ml=70ml=70cm3;
(3)矿石的密度ρ===2.5g/cm3;
在测量矿石体积的过程中,矿石从烧杯中取出,必然出带出一定的水,从而使补充的水量增加,也就是测量的矿石体积会偏大。质量不变,体积偏大,最终的密度就会偏小。
故答案为:(1)取下最小砝码,移动游码;(2)70;(3)2.5×103;
偏小。
