12.2三角形全等的判定 (ASA AAS)同步练习题 2021 —2022学年 人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 12.2三角形全等的判定 (ASA AAS)同步练习题 2021 —2022学年 人教版八年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 20:34:08 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.2三角形全等的判定
同步练习题(ASA
AAS)
一、选择题
1.如图,,点C是的中点,直接应用“”定理证明还需要的条件是(
)
A.
B.
C.
D.
2.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
3.如图,在中,于点D,于点E,与相交于点F,若,则与相等的线段是(
)
A.
B.
C.
D.
4.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是(
)
A.或
B.或
C.或
D.或
5.如图,点C,D在线段AB上,,,添加以下哪一个条件仍不能判定△AED≌△BFC(
)
A.
B.
C.
D.
6.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___.
A.10
B.6
C.5
D.2
7.如图,在△ABC中,AB=AC,AB>BC,点D在BC边上,BD=DC,∠BED=∠CFD=∠BAC,若S△ABC=30,则阴影部分的面积为(
)
A.5
B.10
C.15
D.20
8.如图,垂足为,垂足为与交于点,则的长为(
)
A.
B.
C.
D.
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是( )
A.1.5
B.2
?
C.???????????
?
D.
10.如图,的面积为,垂直的平分线于,则的面积为( )
A.
B.
C.
D.
二、填空题
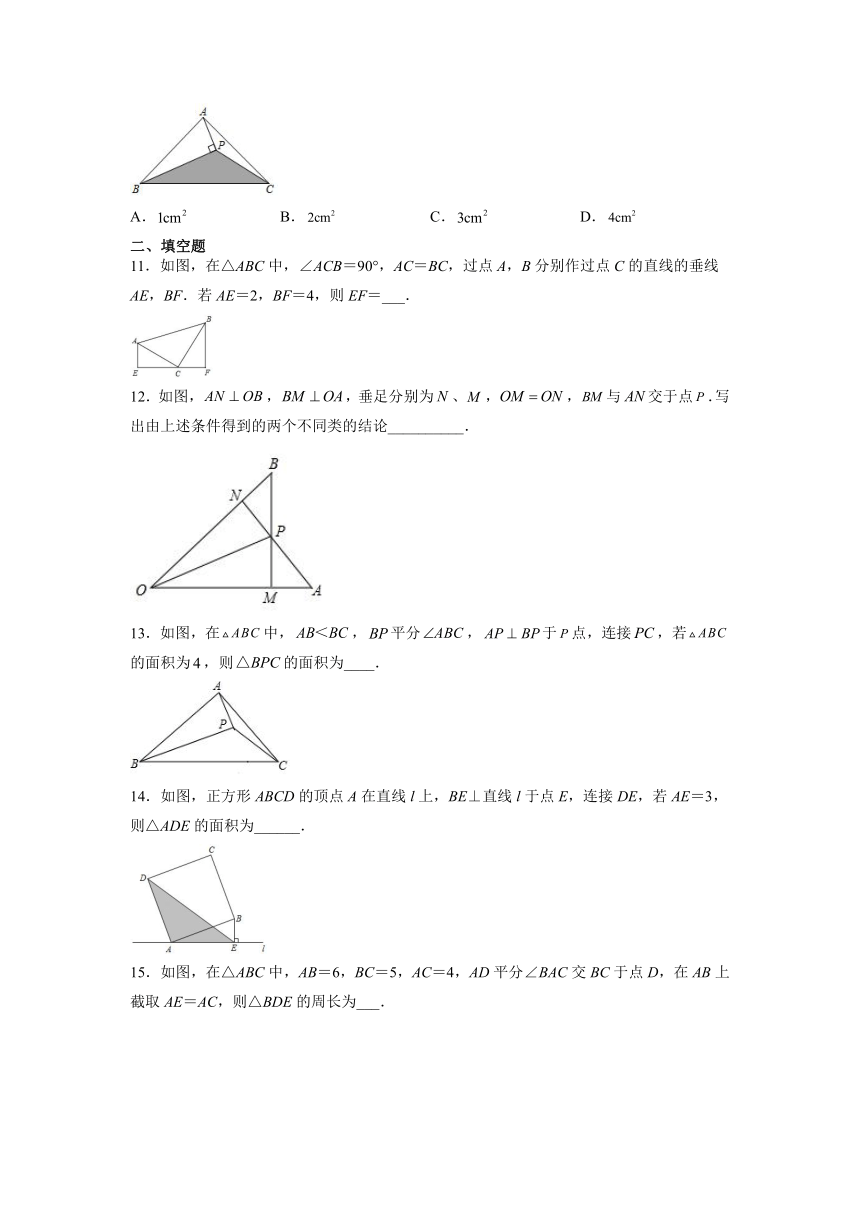
11.如图,在△ABC中,∠ACB=90°,AC=BC,过点A,B分别作过点C的直线的垂线AE,BF.若AE=2,BF=4,则EF=___.
12.如图,,,垂足分别为、,,与交于点.写出由上述条件得到的两个不同类的结论__________.
13.如图,在中,,平分,于点,连接,若的面积为,则的面积为____.
14.如图,正方形ABCD的顶点A在直线l上,BE⊥直线l于点E,连接DE,若AE=3,则△ADE的面积为______.
15.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为___.
三、解答题
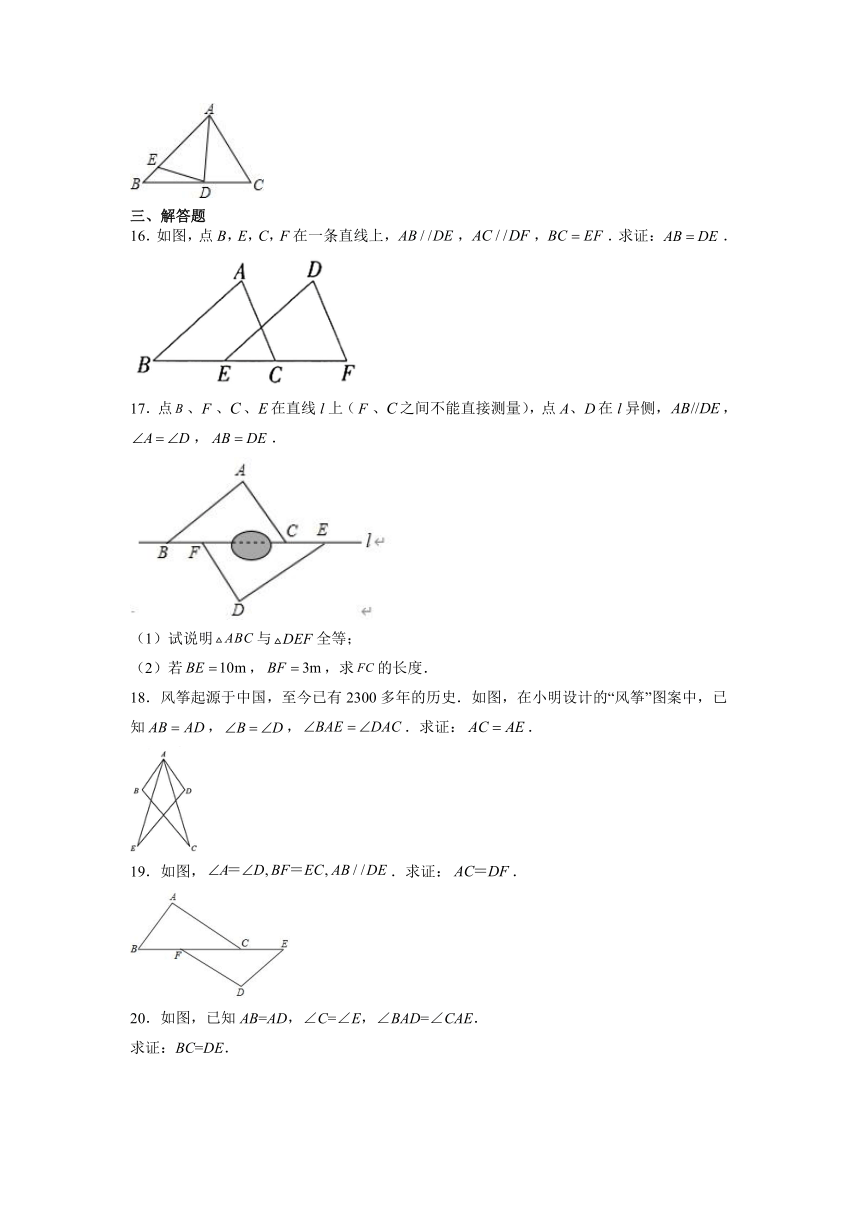
16.如图,点B,E,C,F在一条直线上,,,.求证:.
17.点、、、在直线l上(、之间不能直接测量),点A、在l异侧,,,.
(1)试说明与全等;
(2)若,,求的长度.
18.风筝起源于中国,至今已有2300多年的历史.如图,在小明设计的“风筝”图案中,已知,,.求证:.
19.如图,.求证:.
20.如图,已知AB=AD,∠C=∠E,∠BAD=∠CAE.
求证:BC=DE.
21.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=10,求AC的长.
22.如图,在中,,,,.求证:.
23.在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
将小明看成一条线段AB,河对岸一点为点C,自己所在岸的那个点为点D,示意图如图所示,请你根据示意图帮助小明同学将问题补充完整,并解释其中的道理.
如图,如果AB⊥CD于点A,
,那么AC=AD.说明AC=AD的理由.
【参考答案】
1.B
2.A
3.B
4.C
5.A
6.C
7.D
8.C
9.B
10.C.
11.6
12.PM=PN,∠PON=∠POM(答案不唯一).
13.2
14.
15.7
16.证明:∵,
∴,
∵,
∴.
在和中,
∴(ASA),∴.
17.(1),
∴,
在和中,,
∴
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BC-FC=EF-FC,即BF=CE,
∵,,
∴FC=EF-BF-CE=10-3-3=4m.
18.∵,
∴,
即,
在和中,
.
∴,
∴.
19.证明:∵
,
在和中,
,
,
.
20.证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC.
即∠BAC=∠DAE.
∵AB=AD,∠C=∠E,
∴△ABC≌△ADE.
∴BC=DE.
21.(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
,,
,
在和中,
,
△ACB≌△EBD,;
(2)解:△ACB≌△EBD,
,,
是的中点,
,
,,
,
.
22.证明:∵,,
∴,,
∴,∵,∴,
在和中,
∴(AAS).
易错:证明:,,
∴,,
∴,∴,∴,
在和中,
∴(AAS).
错因:弄错对应角.
满分备考:利用“AAS”证明三角形全等,在书写时,一定要按照“角—角—边”的顺序列出全等的三个条件.
23.如果AB⊥CD,∠ABC=∠ABD,那么AD=AC.
理由如下:
∵AB⊥CD,
∴∠BAD=∠BAC,
在△ABC与△ABD中,
,
∴△ABC≌△ABD(ASA),
∴AC=AD.
故答案为:∠ABC=∠ABD.
第十二章全等三角形
12.2三角形全等的判定
同步练习题(ASA
AAS)
一、选择题
1.如图,,点C是的中点,直接应用“”定理证明还需要的条件是(
)
A.
B.
C.
D.
2.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
3.如图,在中,于点D,于点E,与相交于点F,若,则与相等的线段是(
)
A.
B.
C.
D.
4.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是(
)
A.或
B.或
C.或
D.或
5.如图,点C,D在线段AB上,,,添加以下哪一个条件仍不能判定△AED≌△BFC(
)
A.
B.
C.
D.
6.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___.
A.10
B.6
C.5
D.2
7.如图,在△ABC中,AB=AC,AB>BC,点D在BC边上,BD=DC,∠BED=∠CFD=∠BAC,若S△ABC=30,则阴影部分的面积为(
)
A.5
B.10
C.15
D.20
8.如图,垂足为,垂足为与交于点,则的长为(
)
A.
B.
C.
D.
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是( )
A.1.5
B.2
?
C.???????????
?
D.
10.如图,的面积为,垂直的平分线于,则的面积为( )
A.
B.
C.
D.
二、填空题
11.如图,在△ABC中,∠ACB=90°,AC=BC,过点A,B分别作过点C的直线的垂线AE,BF.若AE=2,BF=4,则EF=___.
12.如图,,,垂足分别为、,,与交于点.写出由上述条件得到的两个不同类的结论__________.
13.如图,在中,,平分,于点,连接,若的面积为,则的面积为____.
14.如图,正方形ABCD的顶点A在直线l上,BE⊥直线l于点E,连接DE,若AE=3,则△ADE的面积为______.
15.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为___.
三、解答题
16.如图,点B,E,C,F在一条直线上,,,.求证:.
17.点、、、在直线l上(、之间不能直接测量),点A、在l异侧,,,.
(1)试说明与全等;
(2)若,,求的长度.
18.风筝起源于中国,至今已有2300多年的历史.如图,在小明设计的“风筝”图案中,已知,,.求证:.
19.如图,.求证:.
20.如图,已知AB=AD,∠C=∠E,∠BAD=∠CAE.
求证:BC=DE.
21.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=10,求AC的长.
22.如图,在中,,,,.求证:.
23.在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
将小明看成一条线段AB,河对岸一点为点C,自己所在岸的那个点为点D,示意图如图所示,请你根据示意图帮助小明同学将问题补充完整,并解释其中的道理.
如图,如果AB⊥CD于点A,
,那么AC=AD.说明AC=AD的理由.
【参考答案】
1.B
2.A
3.B
4.C
5.A
6.C
7.D
8.C
9.B
10.C.
11.6
12.PM=PN,∠PON=∠POM(答案不唯一).
13.2
14.
15.7
16.证明:∵,
∴,
∵,
∴.
在和中,
∴(ASA),∴.
17.(1),
∴,
在和中,,
∴
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BC-FC=EF-FC,即BF=CE,
∵,,
∴FC=EF-BF-CE=10-3-3=4m.
18.∵,
∴,
即,
在和中,
.
∴,
∴.
19.证明:∵
,
在和中,
,
,
.
20.证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC.
即∠BAC=∠DAE.
∵AB=AD,∠C=∠E,
∴△ABC≌△ADE.
∴BC=DE.
21.(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
,,
,
在和中,
,
△ACB≌△EBD,;
(2)解:△ACB≌△EBD,
,,
是的中点,
,
,,
,
.
22.证明:∵,,
∴,,
∴,∵,∴,
在和中,
∴(AAS).
易错:证明:,,
∴,,
∴,∴,∴,
在和中,
∴(AAS).
错因:弄错对应角.
满分备考:利用“AAS”证明三角形全等,在书写时,一定要按照“角—角—边”的顺序列出全等的三个条件.
23.如果AB⊥CD,∠ABC=∠ABD,那么AD=AC.
理由如下:
∵AB⊥CD,
∴∠BAD=∠BAC,
在△ABC与△ABD中,
,
∴△ABC≌△ABD(ASA),
∴AC=AD.
故答案为:∠ABC=∠ABD.
