2021-2022学年人教版八年级数学上册12.2三角形全等的判定(SSS)同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.2三角形全等的判定(SSS)同步练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 334.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 21:20:29 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.2三角形全等的判定
同步练习题(SSS)
一、选择题
1.如图,通过尺规作图,得到,再利用全等三角形的性质,得到了
,那么,根据尺规作图得到的理由是(
)
A.
B.
C.
D.
2.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
3.如图,己知,,可根据三角形全等证得,则三角形全等的依据的(
)
A.
B.
C.
D.
4.如图,已知DC=BC,那么添加下列一个条件后,就能用“SSS”判定△ABC≌△ADC的是( )
A.AD=AB
B.∠BAC=∠DAC
C.BC=AC
D.∠B=∠D=90°
5.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
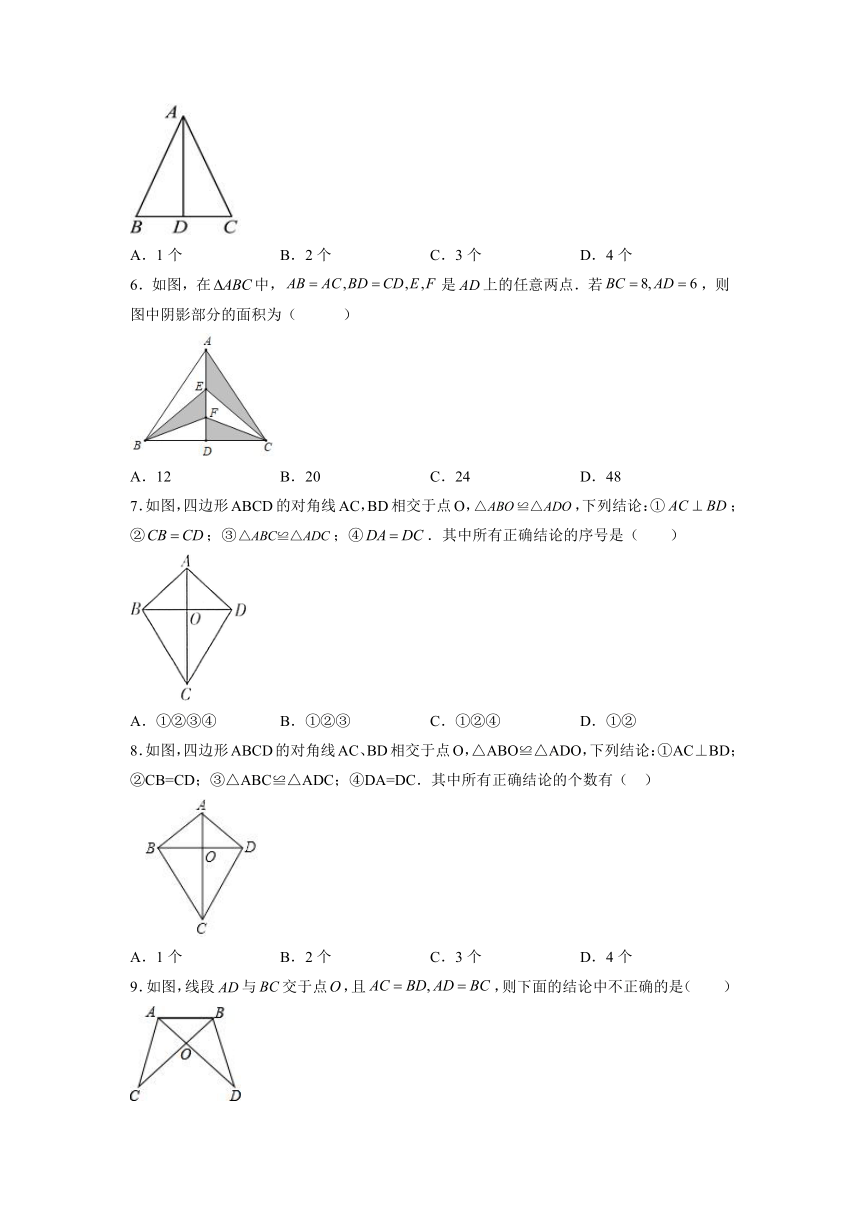
6.如图,在中,是上的任意两点.若,则图中阴影部分的面积为(
)
A.12
B.20
C.24
D.48
7.如图,四边形ABCD的对角线AC,BD相交于点O,,下列结论:①;②;③;④.其中所有正确结论的序号是(
)
A.①②③④
B.①②③
C.①②④
D.①②
8.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有(??
)
A.1个
B.2个
C.3个
D.4个
9.如图,线段与交于点,且,则下面的结论中不正确的是(
)
A.
B.
C.
D.
10.如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
A.5个
B.6个
C.7个
D.8个
二、填空题
11.下列三个命题:①对顶角相等;②全等三角形的对应边相等;③如果两个实数是正数,它们的积是正数.它们的逆命题成立的个数是_____.
12.如图,在△ABC中,已知AD=DE,AB=BE,∠A=85°,∠C=45°,则∠CDE=_____度.
13.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,则说明这两个三角形全等的依据是________.
14.如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD=_____度.
15.如图所示,,,若,则_________.
三、解答题
16.如图,一个特大型设备人字梁,工人师傅要检查人字梁的和是否相等但是他没有测量角度的工具,身边只有一个刻度尺(长度远远不够)他是这样操作的①分别在和上取;②在上取;③量出的长为米,的长为米,如果,则说明和是相等的,他的这种做法合理吗?为什么?
17.如图,,,,求证:.
18.有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
19.如图,平分,点在上,连接、.若,.求证:.
20.已知:如图,点、、、在一条直线上,,,.
(1)求证:;
(2)求证:.
21.如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:△ABC≌△FDE.
22.如图,.
求证:(1);
(2)
23.如图,已知点B,C,D,E在同一直线上,且,,.求证:.
【参考答案】
1.C
2.C
3.B
4.A
5.D
6.A
7.B
8.C
9.B
10.B
11.1
12.40
13.SSS
14.32
15.
16.解:合理,理由:
在和中,
,
,
.
17.∵CE=BF,
∴CE+EF=BF+EF,
∴CF=BE
,
在△AEB和△DFC中,
AB=DC,
AE=DF,
BE=CF,
∴△AEB≌△DFC(SSS),
∴∠AEB=∠DFC,
∴AE∥DF.
18.证明:在△ABC和△ADC中,
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC,
∴AC平分∠BAD.
19.证明:∵AB=AC,BE=CE,AE=AE
∴△ABE≌△ACE(SSS)
∴∠AEB=∠AEC
∴∠1=∠2
20.证明:(1)如图,,
,
即,
,
;
(2)由(1)知
,
.
21.证明:∵A,E,C,F在同一条直线上,AE=FC,
∴AE+EC=EC+FC,
∴AC=EF,
在△ABC和△FDE中,
∴△ABC≌△FDE(SSS).
22.(1)证明:
,即
在和中,
(2)
理由如下:由(1)得:
(内错角相等,两直线平行)
23解析:由条件可先求得,利用SSS判定三角形全等.
答案:证明:∵,
∴,
即,
在和中,
∵
∴(SSS).
第十二章全等三角形
12.2三角形全等的判定
同步练习题(SSS)
一、选择题
1.如图,通过尺规作图,得到,再利用全等三角形的性质,得到了
,那么,根据尺规作图得到的理由是(
)
A.
B.
C.
D.
2.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
3.如图,己知,,可根据三角形全等证得,则三角形全等的依据的(
)
A.
B.
C.
D.
4.如图,已知DC=BC,那么添加下列一个条件后,就能用“SSS”判定△ABC≌△ADC的是( )
A.AD=AB
B.∠BAC=∠DAC
C.BC=AC
D.∠B=∠D=90°
5.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
6.如图,在中,是上的任意两点.若,则图中阴影部分的面积为(
)
A.12
B.20
C.24
D.48
7.如图,四边形ABCD的对角线AC,BD相交于点O,,下列结论:①;②;③;④.其中所有正确结论的序号是(
)
A.①②③④
B.①②③
C.①②④
D.①②
8.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有(??
)
A.1个
B.2个
C.3个
D.4个
9.如图,线段与交于点,且,则下面的结论中不正确的是(
)
A.
B.
C.
D.
10.如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
A.5个
B.6个
C.7个
D.8个
二、填空题
11.下列三个命题:①对顶角相等;②全等三角形的对应边相等;③如果两个实数是正数,它们的积是正数.它们的逆命题成立的个数是_____.
12.如图,在△ABC中,已知AD=DE,AB=BE,∠A=85°,∠C=45°,则∠CDE=_____度.
13.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,则说明这两个三角形全等的依据是________.
14.如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD=_____度.
15.如图所示,,,若,则_________.
三、解答题
16.如图,一个特大型设备人字梁,工人师傅要检查人字梁的和是否相等但是他没有测量角度的工具,身边只有一个刻度尺(长度远远不够)他是这样操作的①分别在和上取;②在上取;③量出的长为米,的长为米,如果,则说明和是相等的,他的这种做法合理吗?为什么?
17.如图,,,,求证:.
18.有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
19.如图,平分,点在上,连接、.若,.求证:.
20.已知:如图,点、、、在一条直线上,,,.
(1)求证:;
(2)求证:.
21.如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:△ABC≌△FDE.
22.如图,.
求证:(1);
(2)
23.如图,已知点B,C,D,E在同一直线上,且,,.求证:.
【参考答案】
1.C
2.C
3.B
4.A
5.D
6.A
7.B
8.C
9.B
10.B
11.1
12.40
13.SSS
14.32
15.
16.解:合理,理由:
在和中,
,
,
.
17.∵CE=BF,
∴CE+EF=BF+EF,
∴CF=BE
,
在△AEB和△DFC中,
AB=DC,
AE=DF,
BE=CF,
∴△AEB≌△DFC(SSS),
∴∠AEB=∠DFC,
∴AE∥DF.
18.证明:在△ABC和△ADC中,
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC,
∴AC平分∠BAD.
19.证明:∵AB=AC,BE=CE,AE=AE
∴△ABE≌△ACE(SSS)
∴∠AEB=∠AEC
∴∠1=∠2
20.证明:(1)如图,,
,
即,
,
;
(2)由(1)知
,
.
21.证明:∵A,E,C,F在同一条直线上,AE=FC,
∴AE+EC=EC+FC,
∴AC=EF,
在△ABC和△FDE中,
∴△ABC≌△FDE(SSS).
22.(1)证明:
,即
在和中,
(2)
理由如下:由(1)得:
(内错角相等,两直线平行)
23解析:由条件可先求得,利用SSS判定三角形全等.
答案:证明:∵,
∴,
即,
在和中,
∵
∴(SSS).
