2021-2022学年苏科新版九年级上册数学《第4章 等可能条件下的概率》单元测试卷(word版有答案)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学《第4章 等可能条件下的概率》单元测试卷(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 08:37:33 | ||
图片预览




文档简介
2021-2022学年苏科新版九年级上册数学《第4章
等可能条件下的概率》单元测试卷
一.选择题
1.小明从一定高度随机掷一枚质地均匀的硬币,他已经掷了两次硬币,结果都是“正面朝上”,那么,从概率的角度分析,小明第三次掷硬币时,( )
A.一定会正面朝上
B.正面朝上的可能性大于反面朝上
C.反面朝上的可能性大于正面朝上
D.正、反面朝上的可能性一样大
2.在有22名男生和20名女生的班级中,随机抽签确定一名学生代表,则下列说法正确的是( )
A.男、女生做代表的可能性一样大
B.男生做代表的可能性较大
C.女生做代表的可能性较大
D.男、女生做代表的可能性的大小不能确定
3.掷一枚质地均匀的硬币100次,下列说法正确的是( )
A.可能50次正面朝上
B.掷2次必有1次正面朝上
C.必有50次正面朝上
D.不可能100次正面朝上
4.标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
A.9个黑球和3个白球
B.10黑球和10个白球
C.12个黑球和6个白球
D.10个黑球和5个白球
5.中央电视台“非常6+1”栏目中有个互动环节,在电视直播现场有三个“金蛋”三个“银蛋”其中只有一个“金蛋”内有礼物,银蛋也是如此.有一个打进电话的观众,选择并打开后得到礼物的可能性是( )
A.
B.
C.
D.
6.甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.
糖果袋子
红色
黄色
绿色
总计
甲袋
2颗
2颗
1颗
5颗
乙袋
4颗
2颗
4颗
10颗
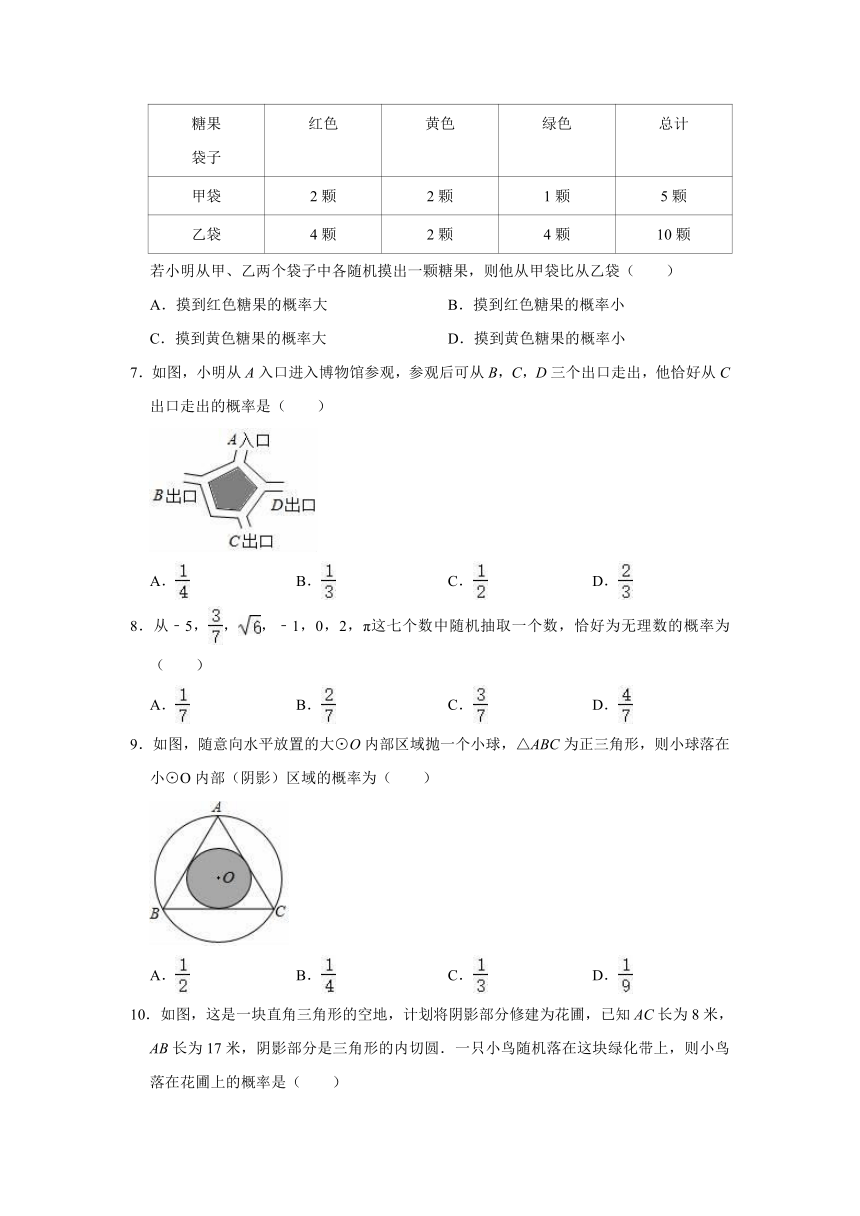
若小明从甲、乙两个袋子中各随机摸出一颗糖果,则他从甲袋比从乙袋( )
A.摸到红色糖果的概率大
B.摸到红色糖果的概率小
C.摸到黄色糖果的概率大
D.摸到黄色糖果的概率小
7.如图,小明从A入口进入博物馆参观,参观后可从B,C,D三个出口走出,他恰好从C出口走出的概率是( )
A.
B.
C.
D.
8.从﹣5,,,﹣1,0,2,π这七个数中随机抽取一个数,恰好为无理数的概率为( )
A.
B.
C.
D.
9.如图,随意向水平放置的大⊙O内部区域抛一个小球,△ABC为正三角形,则小球落在小⊙O内部(阴影)区域的概率为( )
A.
B.
C.
D.
10.如图,这是一块直角三角形的空地,计划将阴影部分修建为花圃,已知AC长为8米,AB长为17米,阴影部分是三角形的内切圆.一只小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率是( )
A.
B.
C.
D.
二.填空题
11.如图所示的点阵中,相邻的四个点构成正方形,小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为
.
12.一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子,向上的一面的点数是1的概率为
.
13.判断下面的说法:如果一件事发生的可能性为百万分之一,那么它就不可能发生
(填“正确”或“错误”)
14.如图有四张不透明卡片,分别写有实数,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是
.
15.有六张正面分别标有数﹣4,﹣2,﹣1,0,1,3的不透明卡片,洗匀后任意摸一张,将卡片上的数字记为a,则使关于x的方程2﹣有正整数解的概率为
.
16.用数字1、2、3随机组成一个三位数,那么组成的三位数是2的倍数的概率是
.
17.如图是客厅里的地毯,被均匀分成16块,除颜色外其他均相同,一小狗跑来停在地毯上,它停在阴影部分的概率为
.
18.初一(2)班共有学生44人,其中男生有30人,女生14人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性
(填“大”或“小”).
19.袋子里装有4个白球、8个红球、m个黑球,每个球除了颜色外都相同.从袋子里任意取一个球,若摸到黑球的可能性最小,则m的值可能是
.
20.在一个不透明的袋中有5个红球、4个黄球、3个白球,每个球除颜色外,其他都相同,从中任意摸出一个球,摸出
(哪种颜色)的可能性最大.
三.解答题
21.在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
22.在一张边长为a的正方形纸板中间有一个面积最大的圆,在圆内涂满了粘苍蝇的药物.如果一只苍蝇飞到正方形纸板上,落在每个点的可能性都相等,求下列事件的概率:
(1)苍蝇被粘住;
(2)苍蝇未被粘住.
23.一个不透明的口袋里有5个除颜色外都相同的球,其中有2个红球,3个黄球.
(1)若从中随意摸出一个球,求摸出红球的可能性;
(2)若要使从中随意摸出一个球是红球的可能性为,求袋子中需再加入几个红球?
24.某厂承接了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级,加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,25元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为27元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,绘制成如图统计图:
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
25.教室的地面是边长为8米和10米的矩形,均匀的铺设了边长是0.4米的正方形地板砖,其中有50块彩色的,某同学的橡皮不慎掉在地上.
则(1)它掉到彩色地板上的概率是多少?
(2)能用扇形的面积来表示概率的大小吗?
26.有12张标有数字2,2,2,3,3,4,4,4,5,5,6,7的卡片,从中任意抽取一张,
(1)抽出的数字是4和5的可能性哪个大?
(2)抽出的数字是奇数和偶数的可能性哪个大?
(3)连续抽5次(抽出后不放回去),抽出的五个数组成的五位数最小可能是多少?
27.请你设计一个有红、白、蓝三种颜色的转盘,使得它停止转动时,指针落在红色区域的可能性比落在白色区域的可能性小,而比落在蓝色区域的可能性大.
参考答案与试题解析
一.选择题
1.解:第三次抛掷硬币不受前两次的影响,仍为正、反面朝上的可能性一样大.
故选:D.
2.解:∵某班有25名男生和18名女生,
∴用抽签方式确定一名学生代表,男生当选的可能性为=,
女生当选的可能性为=,
∴男生当选的可能性大于女生当选的可能性.
故选:B.
3.解:因为一枚质地均匀的硬币只有正反两面,
所以不管抛多少次,硬币正面朝上的概率都是,
所以掷一枚质地均匀的硬币100次,
可能有50次正面向上;
故选:A.
4.解:从A盒子中摸到黑球的可能性是:
9÷(9+3)
=9÷12
=
从B盒子中摸到黑球的可能性是:
10÷(10+10)
=10÷20
=
从C选盒子中摸到黑球的可能性是:
12÷(12+6)
=12÷18
=
从D盒子中摸到黑球的可能性是:
10÷(10+5)
=10÷15
=
∵,
∴最易摸到黑球的是A盒子.
故选:A.
5.解:三个“金蛋”三个“银蛋”其中只有一个“金蛋”内有礼物,银蛋也是如此,有一个打进电话的观众,选择并打开后得到礼物的可能性是为.故选D.
6.解:小明从甲袋子中随机摸出一颗糖果,摸到红色糖果的概率为,摸到黄色糖果的概率为,
从乙袋子中摸出一颗糖果,摸到红色糖果的概率为=,摸到黄色糖果的概率为=,
∵>,
∴小明从甲袋比从乙袋摸到黄色糖果的概率大,
故选:C.
7.解:小明恰好在C出口出来的概率为,
故选:B.
8.解:在﹣5,,,﹣1,0,2,π这七个数中,无理数有,π,共2个数,
则恰好为无理数的概率为.
故选:B.
9.解:∵如图所示的是正三角形,
∴∠ABC=60°,
∴∠OBE=30°,∠OEB=90°,
设OE=a,则OB=2a,
则小球落在小⊙O内部(阴影)区域的概率为=.
故选:B.
10.解:∵△ABC为直角三角形,AC长为8米,AB长为17米,
∴BC=15米,
∴△ABC的内切圆半径==3米,
∴S△ABC=AC?BC=×8×15=60平方米,
S圆=9π平方米,
∴小鸟落在花圃上的概率==π.
故选:A.
二.填空题
11.解:如图所示:
根据题意可知四边形AEFB是正方形,直线MN把正方形AEFB平分分成两份,正方形CDEF的面积与正方形ABFE的面积相同,
所以小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为.
故答案为:.
12.解:由概率公式P(向上一面的点数是1)=.
故答案为:.
13.解:如果一件事发生的机会只有百万分之一,发生的可能性很小但不是不可能发生.
故答案为:错误.
14.解:根据题意可得:5张小卡片上分别写有实数,其中无理数为﹣,π两个,
则从中随机抽取一张卡片,抽到无理数的可能性是.
故答案为:.
15.解:解分式方程得:x=,
∵分式方程的解为正整数,
∴2﹣a>0,
∴a<2,
∴a=﹣4,﹣2,﹣1,0,1,
当a=﹣4,x=1,
当a=﹣2,x=1.5,
∵分式方程的解为正整数,
∴x=1.5不合题意,
当a=﹣1,x=2是增根不合题意,
当a=0时,x=3,
当a=1时,x=6,
∴使关于x的方程2﹣有正整数解的概率为=.
故答案为:.
16.解:用1,2,3三个数字组成一个三位数的所有情况是:123,132,213,231,312,321,其中组成的三位数是2的倍数的有132,312,共2种,所以组成的三位数是2的倍数的概率是=.
故答案为:.
17.解:一小狗跑来停在地毯上,它停在阴影部分的概率为=.
故答案为:.
18.解:∵初一(2)班共有学生44人,其中男生有30人,女生14人,
∴找到男生的概率为:=,
找到女生的概率为:=
∴找到男生的可能性大,
故答案为:大
19.解:从袋中任取一个球,因袋中球的总数一定,故要使摸到红球的可能最大,摸到黑球的可能最小,只需使红球数目最多,而黑球数目最少即可.而黑球数目最少即可,必有m<4,即m=0或1或2或3.
答:m的可能性是0或1或2或3,
故答案为:0或1或2或3.
20.解:因为袋子中有4个红球、3个黄球和5个蓝球,从中任意摸出一个球,
①为红球的概率是;
②为黄球的概率是=;
③为白球的概率是=.
可见摸出红球的可能性大.
故答案为:红球.
三.解答题
21.解:(1)∵袋子中装有9个红球和6个黄球,这些球除颜色外都相同,
∴摸出每一球的可能性相同,
∴摸出红球的概率是,摸出黄球的概率是;
(2)设放入红球x个,则黄球为(7﹣x)个,
由题意得:,
解得:x=2,
则7﹣x=5,
∴放进去的这7个球中红球2个,黄球5个.
22.解:由题意知:在边长为a的正方形中面积最大的圆的半径为a,
所以面积最大的圆的面积为π(a)2=a2,正方形的面积为a2,
(1)苍蝇被粘住的概率为=;
(2)苍蝇未被粘住的概率为1﹣.
23.解:(1)∵从中随意摸出一个球的所有可能的结果个数是5,
随意摸出一个球是红球的结果个数是2,
∴从中随意摸出一个球,摸出红球的可能性是.….(3分)
(2)设需再加入x个红球.
依题意可列:,
解得x=1,
经检验,x=1是分式方程的解,且符合题意,
∴要使从中随意摸出一个球是红球的可能性为,袋子中需再加入1个红球.
24.解:(1)由试加工出来的产品等级的频数分布直方图可得:P(甲分厂加工产品为A等级)=,
P(乙分厂加工产品为A等级)=;
(2)方法一:甲分厂加工出来的100件产品的平均利润为:(40×90+20×50+20×25﹣20×50﹣27×100)÷100=14(元),
乙分厂加工出来的100件产品的平均利润为:(28×90+17×50+34×25﹣21×50﹣20×100)÷100=11.7(元),
因为14>11.7,
所以厂家应选甲分厂承接加工业务.
方法二:由数据可得甲、乙分厂加工出来的100个产品各等级的利润及频数如下:
等级
A
B
C
D
甲分厂利润
63
23
﹣2
﹣77
甲分厂频数
40
20
20
20
因此,甲分厂加工出来的100件产品的平均利润为(元),
等级
A
B
C
D
乙分厂利润
70
30
5
﹣70
乙分厂频数
28
17
34
21
因此,乙分厂加工出来的100件产品的平均利润为:(元),
因为14>11.7,
所以厂家应选甲分厂承接加工业务.
25.解:(1)由题意知:共铺设了地板砖=500块,
故掉在彩色的地板上的概率是=;
(2)能.将一圆分为圆心角为36°和324°的两个扇形即可.
26.解:(1)∵这组数据中,4出现3次,5出现2次,
∴抽到4的可能性大;
(2)∵奇数有5个,偶数有7个,
∴抽到偶数的可能性大;
(3)最小的五位数为:22233;
27.解:如图:白色区域的扇形面积最大,蓝色区域的扇形面积最小.
等可能条件下的概率》单元测试卷
一.选择题
1.小明从一定高度随机掷一枚质地均匀的硬币,他已经掷了两次硬币,结果都是“正面朝上”,那么,从概率的角度分析,小明第三次掷硬币时,( )
A.一定会正面朝上
B.正面朝上的可能性大于反面朝上
C.反面朝上的可能性大于正面朝上
D.正、反面朝上的可能性一样大
2.在有22名男生和20名女生的班级中,随机抽签确定一名学生代表,则下列说法正确的是( )
A.男、女生做代表的可能性一样大
B.男生做代表的可能性较大
C.女生做代表的可能性较大
D.男、女生做代表的可能性的大小不能确定
3.掷一枚质地均匀的硬币100次,下列说法正确的是( )
A.可能50次正面朝上
B.掷2次必有1次正面朝上
C.必有50次正面朝上
D.不可能100次正面朝上
4.标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
A.9个黑球和3个白球
B.10黑球和10个白球
C.12个黑球和6个白球
D.10个黑球和5个白球
5.中央电视台“非常6+1”栏目中有个互动环节,在电视直播现场有三个“金蛋”三个“银蛋”其中只有一个“金蛋”内有礼物,银蛋也是如此.有一个打进电话的观众,选择并打开后得到礼物的可能性是( )
A.
B.
C.
D.
6.甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.
糖果袋子
红色
黄色
绿色
总计
甲袋
2颗
2颗
1颗
5颗
乙袋
4颗
2颗
4颗
10颗
若小明从甲、乙两个袋子中各随机摸出一颗糖果,则他从甲袋比从乙袋( )
A.摸到红色糖果的概率大
B.摸到红色糖果的概率小
C.摸到黄色糖果的概率大
D.摸到黄色糖果的概率小
7.如图,小明从A入口进入博物馆参观,参观后可从B,C,D三个出口走出,他恰好从C出口走出的概率是( )
A.
B.
C.
D.
8.从﹣5,,,﹣1,0,2,π这七个数中随机抽取一个数,恰好为无理数的概率为( )
A.
B.
C.
D.
9.如图,随意向水平放置的大⊙O内部区域抛一个小球,△ABC为正三角形,则小球落在小⊙O内部(阴影)区域的概率为( )
A.
B.
C.
D.
10.如图,这是一块直角三角形的空地,计划将阴影部分修建为花圃,已知AC长为8米,AB长为17米,阴影部分是三角形的内切圆.一只小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率是( )
A.
B.
C.
D.
二.填空题
11.如图所示的点阵中,相邻的四个点构成正方形,小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为
.
12.一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子,向上的一面的点数是1的概率为
.
13.判断下面的说法:如果一件事发生的可能性为百万分之一,那么它就不可能发生
(填“正确”或“错误”)
14.如图有四张不透明卡片,分别写有实数,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是
.
15.有六张正面分别标有数﹣4,﹣2,﹣1,0,1,3的不透明卡片,洗匀后任意摸一张,将卡片上的数字记为a,则使关于x的方程2﹣有正整数解的概率为
.
16.用数字1、2、3随机组成一个三位数,那么组成的三位数是2的倍数的概率是
.
17.如图是客厅里的地毯,被均匀分成16块,除颜色外其他均相同,一小狗跑来停在地毯上,它停在阴影部分的概率为
.
18.初一(2)班共有学生44人,其中男生有30人,女生14人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性
(填“大”或“小”).
19.袋子里装有4个白球、8个红球、m个黑球,每个球除了颜色外都相同.从袋子里任意取一个球,若摸到黑球的可能性最小,则m的值可能是
.
20.在一个不透明的袋中有5个红球、4个黄球、3个白球,每个球除颜色外,其他都相同,从中任意摸出一个球,摸出
(哪种颜色)的可能性最大.
三.解答题
21.在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
22.在一张边长为a的正方形纸板中间有一个面积最大的圆,在圆内涂满了粘苍蝇的药物.如果一只苍蝇飞到正方形纸板上,落在每个点的可能性都相等,求下列事件的概率:
(1)苍蝇被粘住;
(2)苍蝇未被粘住.
23.一个不透明的口袋里有5个除颜色外都相同的球,其中有2个红球,3个黄球.
(1)若从中随意摸出一个球,求摸出红球的可能性;
(2)若要使从中随意摸出一个球是红球的可能性为,求袋子中需再加入几个红球?
24.某厂承接了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级,加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,25元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为27元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,绘制成如图统计图:
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
25.教室的地面是边长为8米和10米的矩形,均匀的铺设了边长是0.4米的正方形地板砖,其中有50块彩色的,某同学的橡皮不慎掉在地上.
则(1)它掉到彩色地板上的概率是多少?
(2)能用扇形的面积来表示概率的大小吗?
26.有12张标有数字2,2,2,3,3,4,4,4,5,5,6,7的卡片,从中任意抽取一张,
(1)抽出的数字是4和5的可能性哪个大?
(2)抽出的数字是奇数和偶数的可能性哪个大?
(3)连续抽5次(抽出后不放回去),抽出的五个数组成的五位数最小可能是多少?
27.请你设计一个有红、白、蓝三种颜色的转盘,使得它停止转动时,指针落在红色区域的可能性比落在白色区域的可能性小,而比落在蓝色区域的可能性大.
参考答案与试题解析
一.选择题
1.解:第三次抛掷硬币不受前两次的影响,仍为正、反面朝上的可能性一样大.
故选:D.
2.解:∵某班有25名男生和18名女生,
∴用抽签方式确定一名学生代表,男生当选的可能性为=,
女生当选的可能性为=,
∴男生当选的可能性大于女生当选的可能性.
故选:B.
3.解:因为一枚质地均匀的硬币只有正反两面,
所以不管抛多少次,硬币正面朝上的概率都是,
所以掷一枚质地均匀的硬币100次,
可能有50次正面向上;
故选:A.
4.解:从A盒子中摸到黑球的可能性是:
9÷(9+3)
=9÷12
=
从B盒子中摸到黑球的可能性是:
10÷(10+10)
=10÷20
=
从C选盒子中摸到黑球的可能性是:
12÷(12+6)
=12÷18
=
从D盒子中摸到黑球的可能性是:
10÷(10+5)
=10÷15
=
∵,
∴最易摸到黑球的是A盒子.
故选:A.
5.解:三个“金蛋”三个“银蛋”其中只有一个“金蛋”内有礼物,银蛋也是如此,有一个打进电话的观众,选择并打开后得到礼物的可能性是为.故选D.
6.解:小明从甲袋子中随机摸出一颗糖果,摸到红色糖果的概率为,摸到黄色糖果的概率为,
从乙袋子中摸出一颗糖果,摸到红色糖果的概率为=,摸到黄色糖果的概率为=,
∵>,
∴小明从甲袋比从乙袋摸到黄色糖果的概率大,
故选:C.
7.解:小明恰好在C出口出来的概率为,
故选:B.
8.解:在﹣5,,,﹣1,0,2,π这七个数中,无理数有,π,共2个数,
则恰好为无理数的概率为.
故选:B.
9.解:∵如图所示的是正三角形,
∴∠ABC=60°,
∴∠OBE=30°,∠OEB=90°,
设OE=a,则OB=2a,
则小球落在小⊙O内部(阴影)区域的概率为=.
故选:B.
10.解:∵△ABC为直角三角形,AC长为8米,AB长为17米,
∴BC=15米,
∴△ABC的内切圆半径==3米,
∴S△ABC=AC?BC=×8×15=60平方米,
S圆=9π平方米,
∴小鸟落在花圃上的概率==π.
故选:A.
二.填空题
11.解:如图所示:
根据题意可知四边形AEFB是正方形,直线MN把正方形AEFB平分分成两份,正方形CDEF的面积与正方形ABFE的面积相同,
所以小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为.
故答案为:.
12.解:由概率公式P(向上一面的点数是1)=.
故答案为:.
13.解:如果一件事发生的机会只有百万分之一,发生的可能性很小但不是不可能发生.
故答案为:错误.
14.解:根据题意可得:5张小卡片上分别写有实数,其中无理数为﹣,π两个,
则从中随机抽取一张卡片,抽到无理数的可能性是.
故答案为:.
15.解:解分式方程得:x=,
∵分式方程的解为正整数,
∴2﹣a>0,
∴a<2,
∴a=﹣4,﹣2,﹣1,0,1,
当a=﹣4,x=1,
当a=﹣2,x=1.5,
∵分式方程的解为正整数,
∴x=1.5不合题意,
当a=﹣1,x=2是增根不合题意,
当a=0时,x=3,
当a=1时,x=6,
∴使关于x的方程2﹣有正整数解的概率为=.
故答案为:.
16.解:用1,2,3三个数字组成一个三位数的所有情况是:123,132,213,231,312,321,其中组成的三位数是2的倍数的有132,312,共2种,所以组成的三位数是2的倍数的概率是=.
故答案为:.
17.解:一小狗跑来停在地毯上,它停在阴影部分的概率为=.
故答案为:.
18.解:∵初一(2)班共有学生44人,其中男生有30人,女生14人,
∴找到男生的概率为:=,
找到女生的概率为:=
∴找到男生的可能性大,
故答案为:大
19.解:从袋中任取一个球,因袋中球的总数一定,故要使摸到红球的可能最大,摸到黑球的可能最小,只需使红球数目最多,而黑球数目最少即可.而黑球数目最少即可,必有m<4,即m=0或1或2或3.
答:m的可能性是0或1或2或3,
故答案为:0或1或2或3.
20.解:因为袋子中有4个红球、3个黄球和5个蓝球,从中任意摸出一个球,
①为红球的概率是;
②为黄球的概率是=;
③为白球的概率是=.
可见摸出红球的可能性大.
故答案为:红球.
三.解答题
21.解:(1)∵袋子中装有9个红球和6个黄球,这些球除颜色外都相同,
∴摸出每一球的可能性相同,
∴摸出红球的概率是,摸出黄球的概率是;
(2)设放入红球x个,则黄球为(7﹣x)个,
由题意得:,
解得:x=2,
则7﹣x=5,
∴放进去的这7个球中红球2个,黄球5个.
22.解:由题意知:在边长为a的正方形中面积最大的圆的半径为a,
所以面积最大的圆的面积为π(a)2=a2,正方形的面积为a2,
(1)苍蝇被粘住的概率为=;
(2)苍蝇未被粘住的概率为1﹣.
23.解:(1)∵从中随意摸出一个球的所有可能的结果个数是5,
随意摸出一个球是红球的结果个数是2,
∴从中随意摸出一个球,摸出红球的可能性是.….(3分)
(2)设需再加入x个红球.
依题意可列:,
解得x=1,
经检验,x=1是分式方程的解,且符合题意,
∴要使从中随意摸出一个球是红球的可能性为,袋子中需再加入1个红球.
24.解:(1)由试加工出来的产品等级的频数分布直方图可得:P(甲分厂加工产品为A等级)=,
P(乙分厂加工产品为A等级)=;
(2)方法一:甲分厂加工出来的100件产品的平均利润为:(40×90+20×50+20×25﹣20×50﹣27×100)÷100=14(元),
乙分厂加工出来的100件产品的平均利润为:(28×90+17×50+34×25﹣21×50﹣20×100)÷100=11.7(元),
因为14>11.7,
所以厂家应选甲分厂承接加工业务.
方法二:由数据可得甲、乙分厂加工出来的100个产品各等级的利润及频数如下:
等级
A
B
C
D
甲分厂利润
63
23
﹣2
﹣77
甲分厂频数
40
20
20
20
因此,甲分厂加工出来的100件产品的平均利润为(元),
等级
A
B
C
D
乙分厂利润
70
30
5
﹣70
乙分厂频数
28
17
34
21
因此,乙分厂加工出来的100件产品的平均利润为:(元),
因为14>11.7,
所以厂家应选甲分厂承接加工业务.
25.解:(1)由题意知:共铺设了地板砖=500块,
故掉在彩色的地板上的概率是=;
(2)能.将一圆分为圆心角为36°和324°的两个扇形即可.
26.解:(1)∵这组数据中,4出现3次,5出现2次,
∴抽到4的可能性大;
(2)∵奇数有5个,偶数有7个,
∴抽到偶数的可能性大;
(3)最小的五位数为:22233;
27.解:如图:白色区域的扇形面积最大,蓝色区域的扇形面积最小.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
