2021-2022人教版八年级数学上册:13.3.2等边三角形 课件(共18张PPT)
文档属性
| 名称 | 2021-2022人教版八年级数学上册:13.3.2等边三角形 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 09:16:50 | ||
图片预览



文档简介
(共18张PPT)
13.3.2
等边三角形
复习旧知
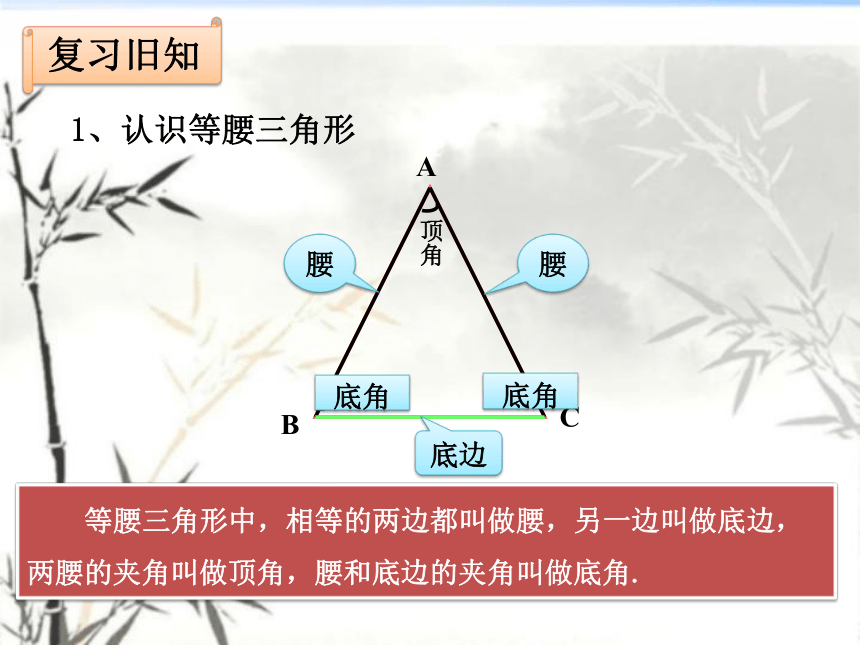
1、认识等腰三角形
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
2、等腰三角形的性质
性质1
等腰三角形的两个底角相等
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(等边对等角);
(三线合一)。
几何符号语言:
∵
AB=AC
∴∠B=∠C
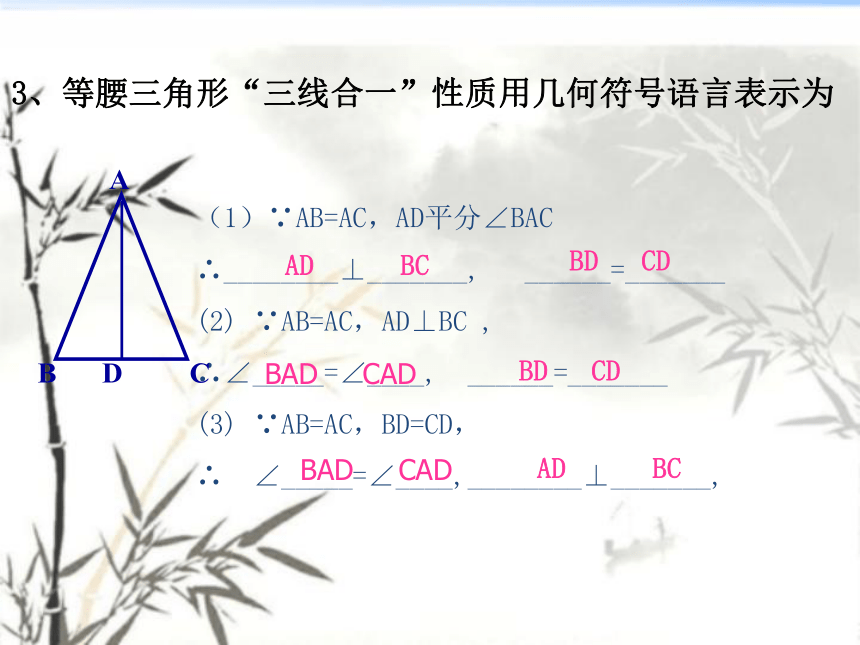
(1)∵AB=AC,AD平分∠BAC
∴________⊥_______,
______=_______
(2)
∵AB=AC,AD⊥BC
,
∴∠_____=∠____,
______=_______
(3)
∵AB=AC,BD=CD,
∴
∠_____=∠____,________⊥_______,
AD
BC
BD
CD
BAD
CAD
BD
CD
BAD
CAD
AD
BC
A
B
C
D
3、等腰三角形“三线合一”性质用几何符号语言表示为
探究新课
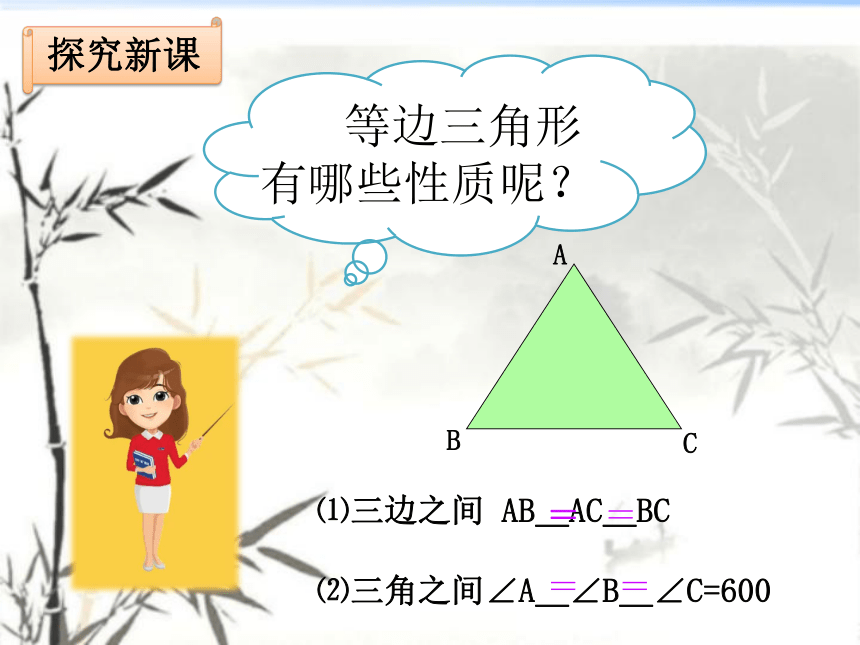
等边三角形有哪些性质呢?
A
B
C
⑴三边之间
AB_AC_BC
⑵三角之间∠A_∠B_∠C=600
=
=
=
=
探究新课
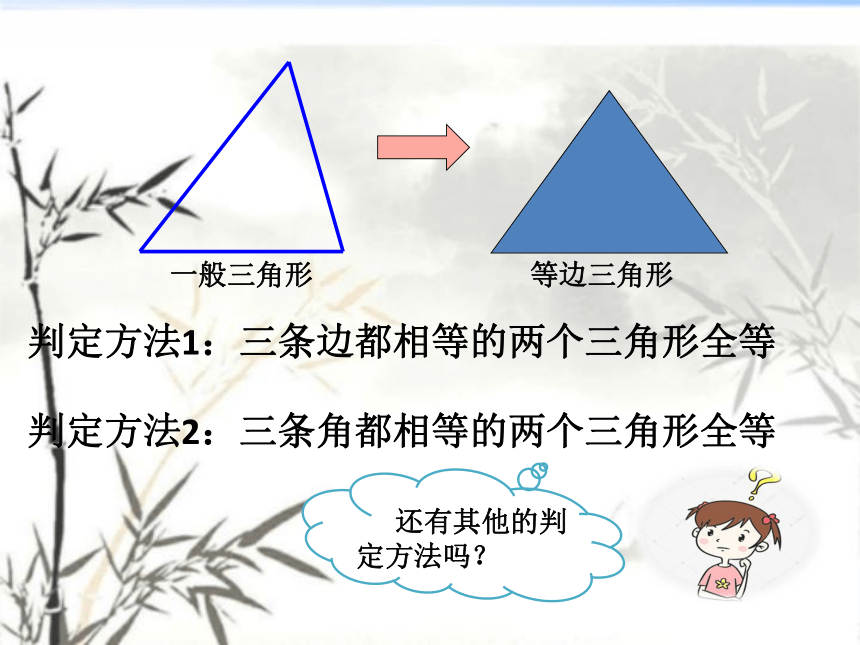
那我们怎么判定一个三角形就是等边三角形呢?
一般三角形
等边三角形
一般三角形
等边三角形
判定方法1:三条边都相等的两个三角形全等
判定方法2:三条角都相等的两个三角形全等
还有其他的判定方法吗?
什么样的等腰三角形是等边三角形呢?
等边三角形
等腰三角形
600
判定方法3:有一个角是600度的等腰三角形是等边三角形
归纳总结
等边三角形的性质是:
等边三角形的判定方法是:
1、三条边都相等
2、三个角都相等
1、三条边都相等的三角形
2、三条角都相等的三角形
3、有一个角是600的等腰三角形
巩固新课
例题:
如图,在等边三角形ABC中,DE∥BC,
请问△ADE是等边三角形吗?试说明理由.
A
C
B
D
E
解:
?ADE是等边三角形
∵?ABC是等边三角形
∴∠A=∠B=∠C
∵
DE∥BC
∴∠ADE=∠B,∠AED=∠C
∴∠ADE==∠AED=∠A
∴?ADE是等边三角形
如图,在等边三角形ABC中,DE∥BC,
请问△ADE是等边三角形吗?试说明理由.
A
C
B
D
E
上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
变式练习
习题训练
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
9
2、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)
A.
4个
B.
5个
C.
6个
D.
7个
D
A
C
B
D
E
O
3、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)
A.
4个
B.
5个
C.
6个
D.
7个
D
A
C
B
D
E
O
4、 若△ABC
是等边三角形点D、E
在边AB、AC
的反向延长线上,且DE∥BC,求证:
∴ △ADE
是等边三角形
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
B
C
D
A
E
5、如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
今天我们主要学习了什么呢?
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法;
2.能够用等边三角形的知识解决相应的数学问题.
课堂小结
图形
等腰三角形
性
质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
轴对称图形(3条)
等边三角形
轴对称图形(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
等边三角形的判定方法是:
1、三条边都相等的三角形
2、三条角都相等的三角形
3、有一个角是600的等腰三角形
13.3.2
等边三角形
复习旧知
1、认识等腰三角形
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
2、等腰三角形的性质
性质1
等腰三角形的两个底角相等
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(等边对等角);
(三线合一)。
几何符号语言:
∵
AB=AC
∴∠B=∠C
(1)∵AB=AC,AD平分∠BAC
∴________⊥_______,
______=_______
(2)
∵AB=AC,AD⊥BC
,
∴∠_____=∠____,
______=_______
(3)
∵AB=AC,BD=CD,
∴
∠_____=∠____,________⊥_______,
AD
BC
BD
CD
BAD
CAD
BD
CD
BAD
CAD
AD
BC
A
B
C
D
3、等腰三角形“三线合一”性质用几何符号语言表示为
探究新课
等边三角形有哪些性质呢?
A
B
C
⑴三边之间
AB_AC_BC
⑵三角之间∠A_∠B_∠C=600
=
=
=
=
探究新课
那我们怎么判定一个三角形就是等边三角形呢?
一般三角形
等边三角形
一般三角形
等边三角形
判定方法1:三条边都相等的两个三角形全等
判定方法2:三条角都相等的两个三角形全等
还有其他的判定方法吗?
什么样的等腰三角形是等边三角形呢?
等边三角形
等腰三角形
600
判定方法3:有一个角是600度的等腰三角形是等边三角形
归纳总结
等边三角形的性质是:
等边三角形的判定方法是:
1、三条边都相等
2、三个角都相等
1、三条边都相等的三角形
2、三条角都相等的三角形
3、有一个角是600的等腰三角形
巩固新课
例题:
如图,在等边三角形ABC中,DE∥BC,
请问△ADE是等边三角形吗?试说明理由.
A
C
B
D
E
解:
?ADE是等边三角形
∵?ABC是等边三角形
∴∠A=∠B=∠C
∵
DE∥BC
∴∠ADE=∠B,∠AED=∠C
∴∠ADE==∠AED=∠A
∴?ADE是等边三角形
如图,在等边三角形ABC中,DE∥BC,
请问△ADE是等边三角形吗?试说明理由.
A
C
B
D
E
上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
变式练习
习题训练
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
9
2、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)
A.
4个
B.
5个
C.
6个
D.
7个
D
A
C
B
D
E
O
3、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)
A.
4个
B.
5个
C.
6个
D.
7个
D
A
C
B
D
E
O
4、 若△ABC
是等边三角形点D、E
在边AB、AC
的反向延长线上,且DE∥BC,求证:
∴ △ADE
是等边三角形
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
B
C
D
A
E
5、如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
今天我们主要学习了什么呢?
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法;
2.能够用等边三角形的知识解决相应的数学问题.
课堂小结
图形
等腰三角形
性
质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
轴对称图形(3条)
等边三角形
轴对称图形(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
等边三角形的判定方法是:
1、三条边都相等的三角形
2、三条角都相等的三角形
3、有一个角是600的等腰三角形
