2021--2022学年湘教版八年级数学上册_ 4.5 一元一次不等式组 课件(共18张PPT)
文档属性
| 名称 | 2021--2022学年湘教版八年级数学上册_ 4.5 一元一次不等式组 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 645.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 09:32:26 | ||
图片预览





文档简介
(共18张PPT)
4.5一元一次不等式组
数学湘教版
八年级上
新知导入
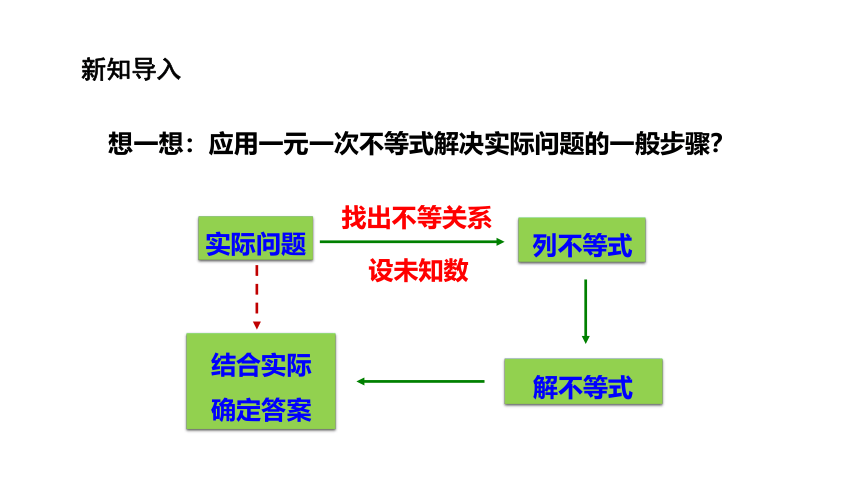
想一想:应用一元一次不等式解决实际问题的一般步骤?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
动脑筋:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球赛?(注:用于国际比赛的足
球场的长在100至110m之间,宽在64至75m之间).
解:设足球场的长为x
m,则它的周长就是2(x+70)m,面积为70x
m2.
本题涉及的数量关系是:
(1)长方形周长>350;(2)长方形面积<7630
注意:这两个不等式要同时成立.
则
2(x+70)>350
和
70x<7630
新知讲解
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350
和70x<7630
像上面这样,把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
新知讲解
讨论:怎样确定上面的不等式组中x的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
新知讲解
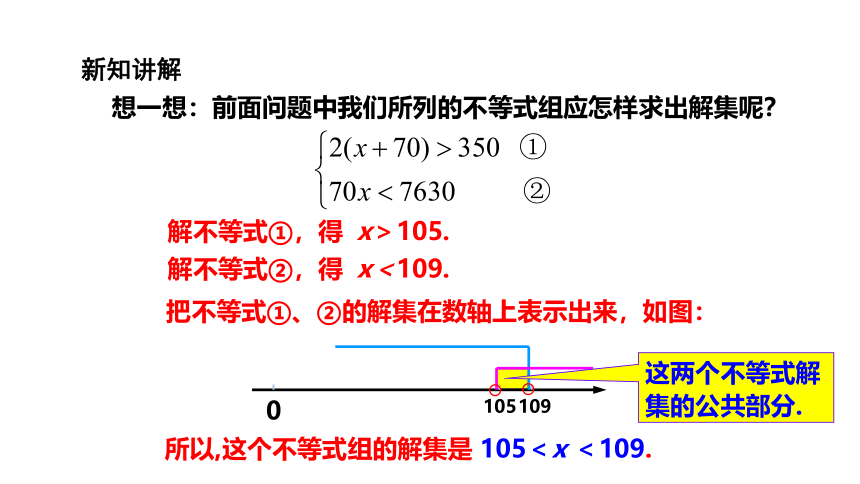
想一想:前面问题中我们所列的不等式组应怎样求出解集呢?
解不等式①,得
解不等式②,得
x>105.
x<109.
把不等式①、②的解集在数轴上表示出来,如图:
0
105
109
所以,这个不等式组的解集是
105<x
<109.
这两个不等式解集的公共部分.
新知讲解
由此可知,这个足球场的长度在105至109m之间,从场地的大小方面来说,可以进行国际足球比赛.
新知讲解
思考:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a
b
a
b
a
b
a
b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
新知讲解
例1:解不等式组:
解不等式①,得
解:
x
≤
3.
解不等式②,得
x
<-3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,
所以,这个不等式组的解集是x<-3.
新知讲解
例2:解不等式组:
解不等式①,得
解:
x
>-2.
解不等式②,得
x
>6.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就是x>6,
所以这个不等式组的解集是x>6.
0
-2
6
新知讲解
例3:解不等式组:
解不等式①,得
解:
x
<-2.
解不等式②,得
x
>3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
3
由图可以看出这两个不等式的解集没有公共部分.
这时,我们说这个不等式组无解.
新知讲解
解不等式②,得
x<6.
练习:解不等式组:
解:
解不等式①,得
把不等式①、②的解集在数轴上表示出来,如图:
3
0
6
因此,原不等式组的解集为
新知讲解
解一元一次不等式组有下列步骤:
(1)求出每个不等式的解集;
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出这几个不等式解集的公共部分;
(4)不等式组的解集就是这个公共部分.
特别注意,没有公共部分则不等式组无解.
新知讲解
1.
填表:
不等式组
不等式组
的解集
x≥4
-2≤x<4
x<-2
无解
课堂练习
x<
(1)解不等式①,得
解:
x
<1.
所以,这个不等式组的解集是
解不等式①,得
(2)
x
<2.
解不等式②,得
x>3;
所以,这个不等式组无解.
解不等式②,得
x<
2.
解下列不等式方程组:
课堂练习
把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分2个,求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
解不等式组,得3.5根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
课堂练习
课堂小结
1、什么是一元一次不等式组?
把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
2、什么是一元一次不等式组的解集?
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
3、解一元一次不等式组的基本步骤是什么?
(1)解每个不等式
(2)在数轴上分别表示各个不等式的解集
(3)利用公共部分确定不等式组的解集
课堂总结
基础作业
教材第150页习题4.5A组第1、2、3题
能力作业
教材第150页习题4.5B组第4题
布置作业
4.5一元一次不等式组
数学湘教版
八年级上
新知导入
想一想:应用一元一次不等式解决实际问题的一般步骤?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
动脑筋:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球赛?(注:用于国际比赛的足
球场的长在100至110m之间,宽在64至75m之间).
解:设足球场的长为x
m,则它的周长就是2(x+70)m,面积为70x
m2.
本题涉及的数量关系是:
(1)长方形周长>350;(2)长方形面积<7630
注意:这两个不等式要同时成立.
则
2(x+70)>350
和
70x<7630
新知讲解
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350
和70x<7630
像上面这样,把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
新知讲解
讨论:怎样确定上面的不等式组中x的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
新知讲解
想一想:前面问题中我们所列的不等式组应怎样求出解集呢?
解不等式①,得
解不等式②,得
x>105.
x<109.
把不等式①、②的解集在数轴上表示出来,如图:
0
105
109
所以,这个不等式组的解集是
105<x
<109.
这两个不等式解集的公共部分.
新知讲解
由此可知,这个足球场的长度在105至109m之间,从场地的大小方面来说,可以进行国际足球比赛.
新知讲解
思考:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a
b
a
b
a
b
a
b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
新知讲解
例1:解不等式组:
解不等式①,得
解:
x
≤
3.
解不等式②,得
x
<-3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,
所以,这个不等式组的解集是x<-3.
新知讲解
例2:解不等式组:
解不等式①,得
解:
x
>-2.
解不等式②,得
x
>6.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就是x>6,
所以这个不等式组的解集是x>6.
0
-2
6
新知讲解
例3:解不等式组:
解不等式①,得
解:
x
<-2.
解不等式②,得
x
>3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
3
由图可以看出这两个不等式的解集没有公共部分.
这时,我们说这个不等式组无解.
新知讲解
解不等式②,得
x<6.
练习:解不等式组:
解:
解不等式①,得
把不等式①、②的解集在数轴上表示出来,如图:
3
0
6
因此,原不等式组的解集为
新知讲解
解一元一次不等式组有下列步骤:
(1)求出每个不等式的解集;
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出这几个不等式解集的公共部分;
(4)不等式组的解集就是这个公共部分.
特别注意,没有公共部分则不等式组无解.
新知讲解
1.
填表:
不等式组
不等式组
的解集
x≥4
-2≤x<4
x<-2
无解
课堂练习
x<
(1)解不等式①,得
解:
x
<1.
所以,这个不等式组的解集是
解不等式①,得
(2)
x
<2.
解不等式②,得
x>3;
所以,这个不等式组无解.
解不等式②,得
x<
2.
解下列不等式方程组:
课堂练习
把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分2个,求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
解不等式组,得3.5
答:学生有4人,苹果有19个.
课堂练习
课堂小结
1、什么是一元一次不等式组?
把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
2、什么是一元一次不等式组的解集?
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
3、解一元一次不等式组的基本步骤是什么?
(1)解每个不等式
(2)在数轴上分别表示各个不等式的解集
(3)利用公共部分确定不等式组的解集
课堂总结
基础作业
教材第150页习题4.5A组第1、2、3题
能力作业
教材第150页习题4.5B组第4题
布置作业
同课章节目录
