河南省临颍县第一重点高中2021-2022学年高二上学期9月月考数学试题(Word版含答案)
文档属性
| 名称 | 河南省临颍县第一重点高中2021-2022学年高二上学期9月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 10:30:21 | ||
图片预览




文档简介
临颍县第一高中2021-2022学年高二上学期9月数学月考试卷
一、单选题
1.某几何体的三视图如图,若该几何体的所有顶点都在一个球面上,则该球的表面积为(
??)
A.?4π??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?20π
2.已知命题p:f(x)=cosx是周期函数;命题q:若m>0,则关于x的方程x2+mx+m=0有两个不相等的实数根.下列说法正确的是(???
)
A.?“p∨q”为真命题??????????B.?“p∧q”为真命题??????????C.?“¬p”为真命题??????????D.?“¬q”为假命题
3.已知函数f(x)=x3+px2+qx与x轴切于x0
点,且极小值为-4,则p+q=(
??)
A.?12?????????????????????????????????????????B.?13?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
4.已知椭圆
上的点M到该椭圆一个焦点F的距离为2,N是MF的中点,O为坐标原点,那么线段ON的长是(???
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?8???????????????????????????????????????????D.?
5.已知椭圆
的左、右焦点分别为
为椭圆上异于端点的任意点,O为坐标原点,
的中点分别为M,N,若四边形
的周长为
,则
的周长是(???
)
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
6.过点
的直线将圆
分成两段圆弧,当两段圆弧中的劣弧所对的圆心角最小时,则该直线的斜率为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
7.三个元件
正常工作的概率分别为
,且是相互独立的.如图,将
两个元件并联后再与
元件串联接入电路,则电路不发生故障的概率是(???
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
8.若关于
的不等式
(
的解集为
,则关于
的不等式
的解集为(???
)
A.
B.
C.
D.
9.我国即将进入双航母时代,航母编队的要求是每艘航母配2~3艘驱逐舰,1~2艘核潜艇.船厂现有5艘驱逐舰和3艘核潜艇全部用来组建航母编队,则不同组建方法种数为(??
)
A.?30????????????????????????????????????????B.?60????????????????????????????????????????C.?90????????????????????????????????????????D.?120
10.下列有关命题的说法中错误的是(???
)
A.?若
为假命题,则p、q均为假命题
B.?“
”是“
”的充分不必要条件
C.?命题“若
,则
“的逆否命题为:“若
,则
”
D.?对于命题p:
,使得
,则
:
,均有
11.已知函数在O,A点处取到极值,其中O是坐标原点,A在曲线上,则曲线的切线的斜率的最大值是(??)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
12.已知函数y=f(x)的图象在区间[a,b]上是连续不断的,如果存在x0∈[a,b],使得
成立,则称x0为函数f(x)在[a,b]上的“好点”,那么函数f(x)=x2+2x在[﹣1,1]上的“好点”的个数为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
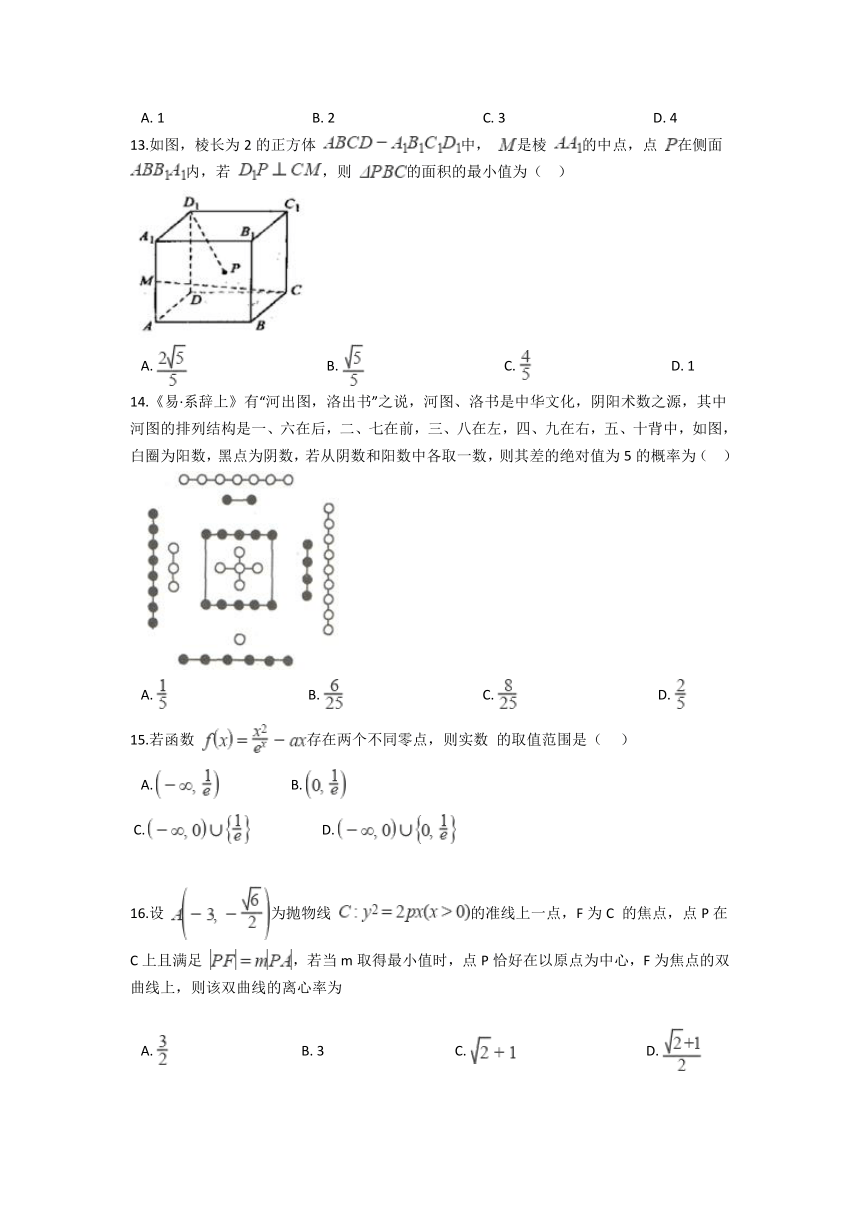
13.如图,棱长为2的正方体
中,
是棱
的中点,点
在侧面
内,若
,则
的面积的最小值为(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?1
14.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为(
??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
15.若函数
存在两个不同零点,则实数
的取值范围是(???
)
A.??????????????????????B.?
?C.??????????????????????D.?
16.设
为抛物线
的准线上一点,F为C
的焦点,点P在C上且满足
,若当m取得最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则该双曲线的离心率为
A.???????????????????????????????????????B.?3??????????????????????????????????????C.???????????????????????????????????????D.?
17.如图,椭圆的左、右顶点分别是A,B,左、右焦点分别是F1
,
F2
,
若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为()
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
18.若函数
在区间
上为减函数,则a的取值范围是(??
)
A.
B.
C.
D.(1,2]
19.定义域为的函数图象上两点是图象上任意一点,其中.已知向量,
若不等式对任意恒成立,则称函数在上“k阶线性近似”.若函数在上“k阶线性近似”,则实数的k取值范围为(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
20.如图,梯形
中,
∥
,
,
,
,将△
沿对角线
折起,设折起后点
的位置为
,使二面角
为直二面角,给出下面四个命题:①
;②三棱锥
的体积为
;③
平面
;④平面
平面
;其中正确命题的个数是(???
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
21.已知在面积为
的△
中,
、
、
分别是三条边
、
、
的中点,点
在直线
上,若
,则
的取值范围是________.
22.若两圆x2+y2=4,x2+y2﹣2mx+m2﹣1=0相外切,则实数m=________.
23.已知曲线y=x2+1,点(n,an)(n∈N+)位于该曲线上,则a10=________.
24.四面体
的四个顶点都在球
的球面上,
平面
,
是等边三角形.若侧面
的面积为
,则球
的表面积的最小值为________.
25.已知点
是椭圆
上一点,
分别为椭圆的左右焦点,过点
作椭圆的切线和
两轴分别交于点
,当
(
为坐标原点)的面积最小时,
,则椭圆的离心率为________.
26.已知曲线
在
处的切线为
,曲线
在
处的切线为
,且
,则
的取值范围是________.
27.若
,则
的最大值为________
28.若直线l:
与x轴相交于点A,与y轴相交于B,被圆
截得的弦长为4,则
为坐标原点的最小值为________.
三、解答题
29.如图,四面体ABCD中,平面DAC⊥底面ABC,
,AD=CD=
,O是AC的中点,E是BD的中点.
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
30.在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖;某顾客从此10张券中任取2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值
(元)的概率分布列.
31.已知数列
满足
且
.
(1)求数列
的通项公式;
(2)令
,若数列
满足
,其前
项和为
,求证:
.
32.已知函数
,
,
.
(1)讨论函数
的单调性;
(2)若函数
有两个极值点,试判断函数
的零点个数.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
A
3.【答案】
C
4.【答案】
B
5.【答案】
A
6.【答案】
C
7.【答案】
A
8.【答案】
D
9.【答案】
D
10.【答案】
A
11.【答案】
A
12.【答案】B
13.【答案】
A
14.【答案】
A
15.【答案】
C
16.【答案】
B
17.【答案】
C
18.【答案】
A
19.【答案】
C
20.【答案】
C
二、填空题
21.【答案】
22.【答案】
±3
23.【答案】101
24.【答案】
25.【答案】
26.【答案】
(-∞,-1)
27.【答案】
28.【答案】
三、解答题
29.【答案】
(1)证明:∵
AD=CD=
,O是AC的中点,
∴
DO⊥AC.
∵
平面DAC⊥底面ABC,平面DAC∩底面ABC=AC,
∴
DO⊥底面ABC
(2)解:由条件易知DO⊥BO,BO⊥AC.
OA=OC=OD=2,
OB=
如图,以点O为坐标原点,OA为x轴,
OB为y轴,OC为z轴建立空间直角坐标系.
则
,
,
,
,
,
,
,
.
设平面ADE的一个法向量为
,
则
即
令
,则
,所以
.
同理可得平面AEC的一个法向量
.
.
因为二面角D-AE-C的平面角为锐角,所以二面角D-AE-C的余弦值为
30.【答案】
(1)解:
,即该顾客中奖的概率为
(2)解:
的所有可能值为0,10,20,50,60,
,
,
,
,
,
故
的分布列为:
0
10
20
50
60
31.【答案】
(1)计算
,
,
,猜想
数学归纳法证明:
⑴当
时,
满足通项公式
⑵假设
猜想成立,即
那么
∴当
时猜想也成立
根据(1)和(2),可知猜想对任何
都成立
解法2:
∴
是以首项为1公差为1的等差数列
求得
(2)由(1)知,
,则
32.【答案】
(1)解:由题意可知函数
的定义域为
当
时:
,所以
单调递增;
当
时:
,所以
单调递减;
所以当
时,
单调递增,当
时,
单调递减.
(2)解:由题意得:
有两个不同的零点,即
有两个不同的根设为
,由(1)得
当
时
单调递增;当
时
单调递减;有
当
时
,所以
时,有
使
且函数
在
单调递减,在
单调递增,
现只需比较
的正负进而确定零点个数.
有
且
且
,即
,
.
令
则
所以函数
在
上单调增,所以
时
时
又
时
时
所以函数有三个零点.
一、单选题
1.某几何体的三视图如图,若该几何体的所有顶点都在一个球面上,则该球的表面积为(
??)
A.?4π??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?20π
2.已知命题p:f(x)=cosx是周期函数;命题q:若m>0,则关于x的方程x2+mx+m=0有两个不相等的实数根.下列说法正确的是(???
)
A.?“p∨q”为真命题??????????B.?“p∧q”为真命题??????????C.?“¬p”为真命题??????????D.?“¬q”为假命题
3.已知函数f(x)=x3+px2+qx与x轴切于x0
点,且极小值为-4,则p+q=(
??)
A.?12?????????????????????????????????????????B.?13?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
4.已知椭圆
上的点M到该椭圆一个焦点F的距离为2,N是MF的中点,O为坐标原点,那么线段ON的长是(???
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?8???????????????????????????????????????????D.?
5.已知椭圆
的左、右焦点分别为
为椭圆上异于端点的任意点,O为坐标原点,
的中点分别为M,N,若四边形
的周长为
,则
的周长是(???
)
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
6.过点
的直线将圆
分成两段圆弧,当两段圆弧中的劣弧所对的圆心角最小时,则该直线的斜率为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
7.三个元件
正常工作的概率分别为
,且是相互独立的.如图,将
两个元件并联后再与
元件串联接入电路,则电路不发生故障的概率是(???
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
8.若关于
的不等式
(
的解集为
,则关于
的不等式
的解集为(???
)
A.
B.
C.
D.
9.我国即将进入双航母时代,航母编队的要求是每艘航母配2~3艘驱逐舰,1~2艘核潜艇.船厂现有5艘驱逐舰和3艘核潜艇全部用来组建航母编队,则不同组建方法种数为(??
)
A.?30????????????????????????????????????????B.?60????????????????????????????????????????C.?90????????????????????????????????????????D.?120
10.下列有关命题的说法中错误的是(???
)
A.?若
为假命题,则p、q均为假命题
B.?“
”是“
”的充分不必要条件
C.?命题“若
,则
“的逆否命题为:“若
,则
”
D.?对于命题p:
,使得
,则
:
,均有
11.已知函数在O,A点处取到极值,其中O是坐标原点,A在曲线上,则曲线的切线的斜率的最大值是(??)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
12.已知函数y=f(x)的图象在区间[a,b]上是连续不断的,如果存在x0∈[a,b],使得
成立,则称x0为函数f(x)在[a,b]上的“好点”,那么函数f(x)=x2+2x在[﹣1,1]上的“好点”的个数为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
13.如图,棱长为2的正方体
中,
是棱
的中点,点
在侧面
内,若
,则
的面积的最小值为(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?1
14.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为(
??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
15.若函数
存在两个不同零点,则实数
的取值范围是(???
)
A.??????????????????????B.?
?C.??????????????????????D.?
16.设
为抛物线
的准线上一点,F为C
的焦点,点P在C上且满足
,若当m取得最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则该双曲线的离心率为
A.???????????????????????????????????????B.?3??????????????????????????????????????C.???????????????????????????????????????D.?
17.如图,椭圆的左、右顶点分别是A,B,左、右焦点分别是F1
,
F2
,
若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为()
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
18.若函数
在区间
上为减函数,则a的取值范围是(??
)
A.
B.
C.
D.(1,2]
19.定义域为的函数图象上两点是图象上任意一点,其中.已知向量,
若不等式对任意恒成立,则称函数在上“k阶线性近似”.若函数在上“k阶线性近似”,则实数的k取值范围为(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
20.如图,梯形
中,
∥
,
,
,
,将△
沿对角线
折起,设折起后点
的位置为
,使二面角
为直二面角,给出下面四个命题:①
;②三棱锥
的体积为
;③
平面
;④平面
平面
;其中正确命题的个数是(???
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
21.已知在面积为
的△
中,
、
、
分别是三条边
、
、
的中点,点
在直线
上,若
,则
的取值范围是________.
22.若两圆x2+y2=4,x2+y2﹣2mx+m2﹣1=0相外切,则实数m=________.
23.已知曲线y=x2+1,点(n,an)(n∈N+)位于该曲线上,则a10=________.
24.四面体
的四个顶点都在球
的球面上,
平面
,
是等边三角形.若侧面
的面积为
,则球
的表面积的最小值为________.
25.已知点
是椭圆
上一点,
分别为椭圆的左右焦点,过点
作椭圆的切线和
两轴分别交于点
,当
(
为坐标原点)的面积最小时,
,则椭圆的离心率为________.
26.已知曲线
在
处的切线为
,曲线
在
处的切线为
,且
,则
的取值范围是________.
27.若
,则
的最大值为________
28.若直线l:
与x轴相交于点A,与y轴相交于B,被圆
截得的弦长为4,则
为坐标原点的最小值为________.
三、解答题
29.如图,四面体ABCD中,平面DAC⊥底面ABC,
,AD=CD=
,O是AC的中点,E是BD的中点.
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
30.在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖;某顾客从此10张券中任取2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值
(元)的概率分布列.
31.已知数列
满足
且
.
(1)求数列
的通项公式;
(2)令
,若数列
满足
,其前
项和为
,求证:
.
32.已知函数
,
,
.
(1)讨论函数
的单调性;
(2)若函数
有两个极值点,试判断函数
的零点个数.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
A
3.【答案】
C
4.【答案】
B
5.【答案】
A
6.【答案】
C
7.【答案】
A
8.【答案】
D
9.【答案】
D
10.【答案】
A
11.【答案】
A
12.【答案】B
13.【答案】
A
14.【答案】
A
15.【答案】
C
16.【答案】
B
17.【答案】
C
18.【答案】
A
19.【答案】
C
20.【答案】
C
二、填空题
21.【答案】
22.【答案】
±3
23.【答案】101
24.【答案】
25.【答案】
26.【答案】
(-∞,-1)
27.【答案】
28.【答案】
三、解答题
29.【答案】
(1)证明:∵
AD=CD=
,O是AC的中点,
∴
DO⊥AC.
∵
平面DAC⊥底面ABC,平面DAC∩底面ABC=AC,
∴
DO⊥底面ABC
(2)解:由条件易知DO⊥BO,BO⊥AC.
OA=OC=OD=2,
OB=
如图,以点O为坐标原点,OA为x轴,
OB为y轴,OC为z轴建立空间直角坐标系.
则
,
,
,
,
,
,
,
.
设平面ADE的一个法向量为
,
则
即
令
,则
,所以
.
同理可得平面AEC的一个法向量
.
.
因为二面角D-AE-C的平面角为锐角,所以二面角D-AE-C的余弦值为
30.【答案】
(1)解:
,即该顾客中奖的概率为
(2)解:
的所有可能值为0,10,20,50,60,
,
,
,
,
,
故
的分布列为:
0
10
20
50
60
31.【答案】
(1)计算
,
,
,猜想
数学归纳法证明:
⑴当
时,
满足通项公式
⑵假设
猜想成立,即
那么
∴当
时猜想也成立
根据(1)和(2),可知猜想对任何
都成立
解法2:
∴
是以首项为1公差为1的等差数列
求得
(2)由(1)知,
,则
32.【答案】
(1)解:由题意可知函数
的定义域为
当
时:
,所以
单调递增;
当
时:
,所以
单调递减;
所以当
时,
单调递增,当
时,
单调递减.
(2)解:由题意得:
有两个不同的零点,即
有两个不同的根设为
,由(1)得
当
时
单调递增;当
时
单调递减;有
当
时
,所以
时,有
使
且函数
在
单调递减,在
单调递增,
现只需比较
的正负进而确定零点个数.
有
且
且
,即
,
.
令
则
所以函数
在
上单调增,所以
时
时
又
时
时
所以函数有三个零点.
同课章节目录
