福建省仙游县智华高级中学2020-2021学年高一下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 福建省仙游县智华高级中学2020-2021学年高一下学期期末考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 12:07:16 | ||
图片预览



文档简介
智华高级中学2020-2021学年高一下学期期末考试
数学试卷
考试时间:120分钟
试卷总分:150分
第Ⅰ卷(选择题、填空题)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
1.
已知复数满足(为虚数单位),则复数在复平面内对应的点所在的象限为(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2.
已知向量,,则(
)
A.
4
B.
5
C.
6
D.
7
3.
某学校采购了10000只口罩,其中蓝色、粉色、白色的比例为,若采用分层抽样的方法,取出500只分发给高一年级学生使用,则抽到白色口罩的只数为(
)
A.
300
B.
250
C.
200
D.
100
4.
设,是两个不同平面,,是两条不同直线,下列命题中正确的是(
)
A.
如果,,,那么
B.
如果,,,那么
C.
如果,,,那么
D.
如果,与所成的角和与所成的角相等,那么
5.
中,,,,则的面积等于(
)
A.
B.
C.
或
D.
或
6.
甲、乙两人练习射击,命中目标的概率分别为和,甲、乙两人各射击一次,有下列说法:①目标恰好被命中一次的概率为;②目标恰好被命中两次的概率为;③目标被命中的概率为;④目标被命中的概率为.以上说法正确的序号依次是(
)
A.
②③
B.
①②③
C.
②④
D.
①③
7.
在正三棱锥中,、分别是棱、的中点,且,若侧棱,则正三棱锥外接球的体积是(
)
A.
B.
C.
D.
8.
已知为在平面内的一点,,,若点在线段上运动,则的最小值为(
)
A.
B.
-12
C.
D.
-4
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有2个选项符合题目要求,不选或含有错误选项的得0分,只选出部分正确选项的得2分,正确选项全部选出的得5分.
9.
下图是我国2011—2020年载货汽车产量及增长趋势统计图,针对这10年的数据,下列说法正确的是(
)
A.
与2019年相比较,2020年我国载货汽车产量同比增速不到
B.
这10年中,载货汽车的同比增速有增有减
C.
这10年我国载货汽车产量的极差超过150万辆
D.
这10年我国载货汽车产量的中位数不超过340万辆
10.
设为复数,则下列命题中正确的是(
)
A.
B.
C.
若,则的最小值为0
D.
若,则
11.
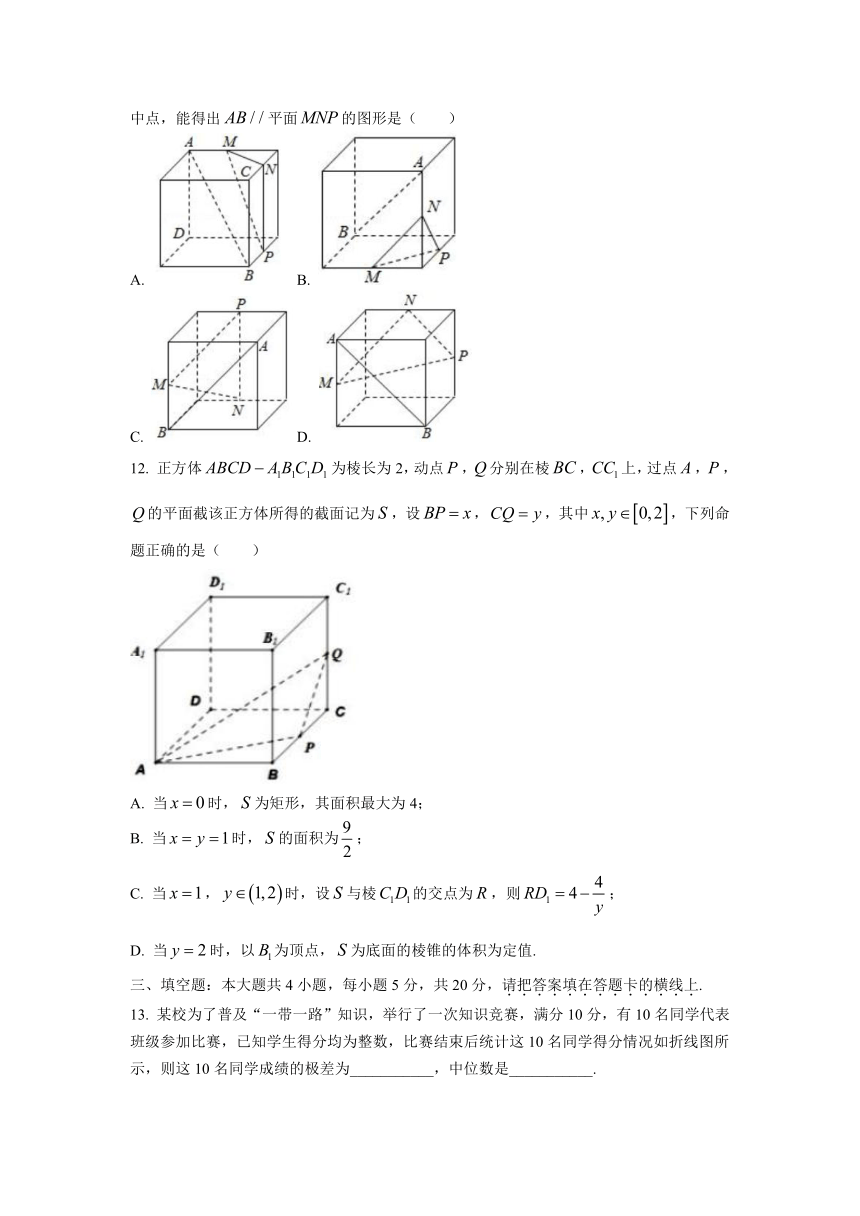
下列四个正方体图形中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形是(
)
A.
B.
C.
D.
12.
正方体为棱长为2,动点,分别在棱,上,过点,,的平面截该正方体所得的截面记为,设,,其中,下列命题正确的是(
)
A.
当时,为矩形,其面积最大为4;
B.
当时,的面积为;
C.
当,时,设与棱的交点为,则;
D.
当时,以为顶点,为底面的棱锥的体积为定值.
三、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.
13.
某校为了普及“一带一路”知识,举行了一次知识竞赛,满分10分,有10名同学代表班级参加比赛,已知学生得分均为整数,比赛结束后统计这10名同学得分情况如折线图所示,则这10名同学成绩的极差为___________,中位数是___________.
14.
已知直角三角形的两直角边长分别为和,则以斜边为轴旋转一周所得几何体的体积为__________.
15.
某汽车站每天均有3辆开往某景点的分为上、中、下等级的客车,某天吴先生准备在该汽车站乘车前往该景点,但他不知道客车的车况,也不知道发车顺序,为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好,则上第二辆,否则上第三辆,那么他乘上上等车的概率为__________.
16.
已知,向量满足,当向量,夹角最大时,__________.
第Ⅱ卷(解答题)
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.
17.
如图,在三棱柱中,侧棱底面,,为的中点,.
(1)求证:平面;
(2)过点作于点,求证:直线平面.
18.
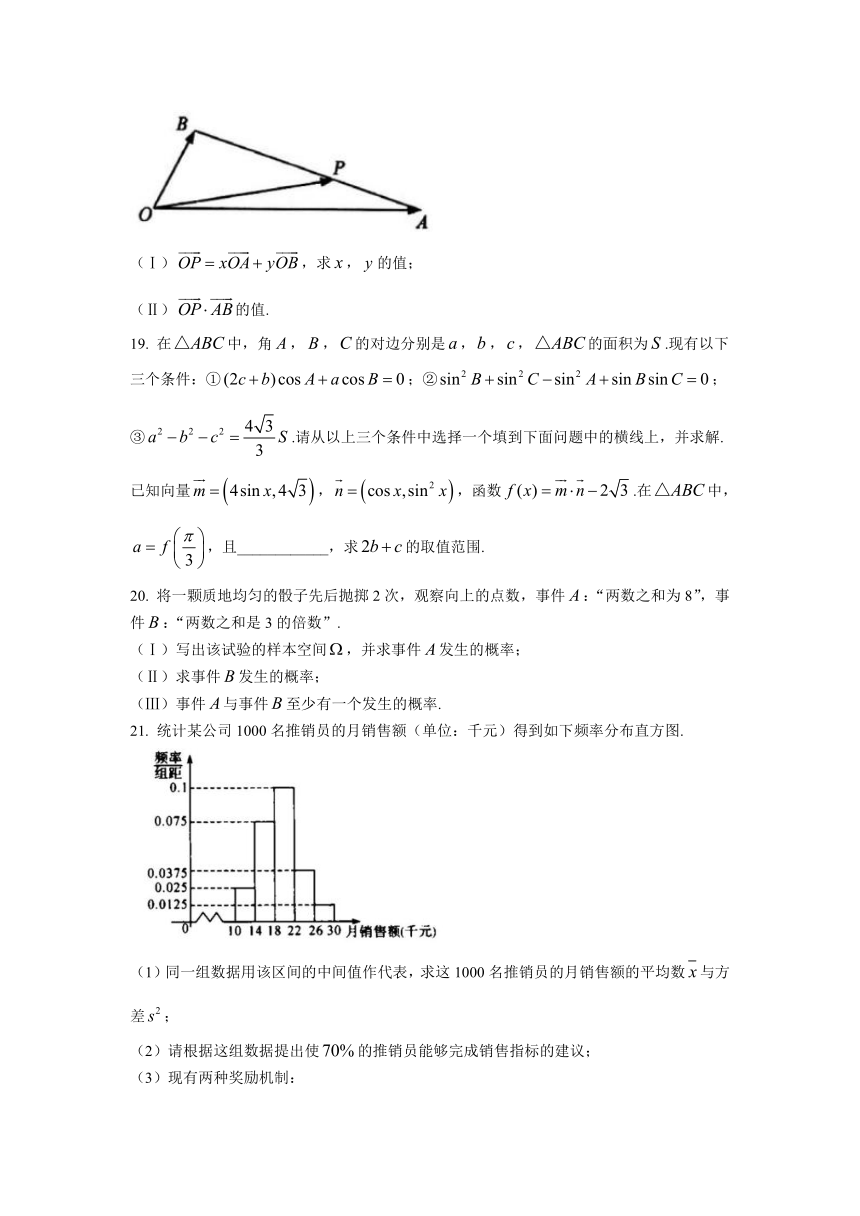
如图,在中,为边上的一点,,,,且与的夹角为.
(Ⅰ),求,的值;
(Ⅱ)的值.
19.
在中,角,,的对边分别是,,,的面积为.现有以下三个条件:①;②;③.请从以上三个条件中选择一个填到下面问题中的横线上,并求解.
已知向量,,函数.在中,,且____________,求的取值范围.
20.
将一颗质地均匀的骰子先后抛掷2次,观察向上的点数,事件:“两数之和为8”,事件:“两数之和是3的倍数”.
(Ⅰ)写出该试验的样本空间,并求事件发生的概率;
(Ⅱ)求事件发生的概率;
(Ⅲ)事件与事件至少有一个发生的概率.
21.
统计某公司1000名推销员的月销售额(单位:千元)得到如下频率分布直方图.
(1)同一组数据用该区间的中间值作代表,求这1000名推销员的月销售额的平均数与方差;
(2)请根据这组数据提出使的推销员能够完成销售指标的建议;
(3)现有两种奖励机制:
方案一:设,销售额落在左侧,每人每月奖励0.4千元;销售额落在内,每人每月奖励0.6千元;销售额落在右侧,每人每月奖励0.8千元.
方案二:每人每月奖励其月销售额的.
用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据:)
记:(其中为对应的频率).
22.
如图,四边形是圆柱的轴截面,点为底面圆周上异于,的点.
(1)求证:平面;
(2)若圆柱的侧面积为,体积为,点为线段上靠近点的三等分点,设,是否存在角使得直线与平面所成角的正弦值最大?若存在,求出相应的正弦值,并求出;若不存在,说明理由.
参考答案
一、选择题:(1-8小题单选,9-12小题多选)
1-5:DBDCD
6-8:CAB
9.
ABC
10.
ACD
11.
AD
12.
BCD
三、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.
13.
7;6
14.
15.
16.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.
17.(1)证明:连接,设,连接,
∵是平行四边形,∴点是的中点,
∵是的中点,∴是的中位线,
∴,
又平面,平面,
∴平面.
(2)∵平面,平面,∴,
又,,
∴直线平面.
解法2:
∵平面,平面,∴平面平面,
又平面平面,,平面,
∴直线平面.
18.(1)如下图,过点作,分别交,点,,
因为,所以,
所以,,
又四边形为平行四边形,所以,
又因为,不共线,所以,.
(2)由(1)知
.
19.
解:.
又.
选择①:,由正弦定理可得:
,故可得,又,
故可得,又,故.
(选择②:,由正弦定理得:
,由余弦定理得,有,故.
选择③:,由面积公式以及余弦定理可得:
,解得,又,故可.
故不论选择哪个条件,都有.)
又.则.
故
,
又,故,
故,故.
20.
解:(Ⅰ)将一颗骰子先后抛掷2次,观察向上的点数,
,共有36个样本点,
它们是等可能的,故这是个古典概型.
,共5个样本点,
∴事件发生的概率为.
(Ⅱ),
共12个样本点.
∴事件发生的概率.
(Ⅲ)事件与事件至少有一个发生,即事件,
,共17个样本点,
∴事件与事件至少有一个发生的概率为.
解法二:因为、不可能同时发生,即、互斥,
所以.
21.(1)由频率分布直方图可得,这1000名推销员的月销售额的平均数为
(万元).
方差为
.
(2)∵,
∴设月销售额为,则,
则,解得,
故根据这组数据可知:将销售指标定为21千元时,才能够使的推销员完成销售指标.
(3)方案一:由(1)可得,,∴,
则当时,,
当时,,
当时,,
1000名推销员的奖励金共计(千元),
方案二:1000名推销员的奖励金(千元),
因为,
所以选择方案一,公司需提供更多的奖励金.
22.
解:(1)证明:因为是圆的直径,点是圆周上一点,
所以,即,
又在圆柱中,母线底面,底面,所以,
又,平面,平面,
所以平面.
(2)设圆柱底面半径为,母线为,则,解得,
在中,过作交于点.
由(1)知平面,因为平面,所以,
又,
所以平面.
若与不重合,即为直线与平面所成的角.
若与重合,直线与平面所成的角为,
设,,
则在中,,
在中,,.
于是
.
当且仅当,即,时,等号成立.
故时,直线与平面所成的角的正弦值最大,最大值为1.
数学试卷
考试时间:120分钟
试卷总分:150分
第Ⅰ卷(选择题、填空题)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
1.
已知复数满足(为虚数单位),则复数在复平面内对应的点所在的象限为(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2.
已知向量,,则(
)
A.
4
B.
5
C.
6
D.
7
3.
某学校采购了10000只口罩,其中蓝色、粉色、白色的比例为,若采用分层抽样的方法,取出500只分发给高一年级学生使用,则抽到白色口罩的只数为(
)
A.
300
B.
250
C.
200
D.
100
4.
设,是两个不同平面,,是两条不同直线,下列命题中正确的是(
)
A.
如果,,,那么
B.
如果,,,那么
C.
如果,,,那么
D.
如果,与所成的角和与所成的角相等,那么
5.
中,,,,则的面积等于(
)
A.
B.
C.
或
D.
或
6.
甲、乙两人练习射击,命中目标的概率分别为和,甲、乙两人各射击一次,有下列说法:①目标恰好被命中一次的概率为;②目标恰好被命中两次的概率为;③目标被命中的概率为;④目标被命中的概率为.以上说法正确的序号依次是(
)
A.
②③
B.
①②③
C.
②④
D.
①③
7.
在正三棱锥中,、分别是棱、的中点,且,若侧棱,则正三棱锥外接球的体积是(
)
A.
B.
C.
D.
8.
已知为在平面内的一点,,,若点在线段上运动,则的最小值为(
)
A.
B.
-12
C.
D.
-4
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有2个选项符合题目要求,不选或含有错误选项的得0分,只选出部分正确选项的得2分,正确选项全部选出的得5分.
9.
下图是我国2011—2020年载货汽车产量及增长趋势统计图,针对这10年的数据,下列说法正确的是(
)
A.
与2019年相比较,2020年我国载货汽车产量同比增速不到
B.
这10年中,载货汽车的同比增速有增有减
C.
这10年我国载货汽车产量的极差超过150万辆
D.
这10年我国载货汽车产量的中位数不超过340万辆
10.
设为复数,则下列命题中正确的是(
)
A.
B.
C.
若,则的最小值为0
D.
若,则
11.
下列四个正方体图形中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形是(
)
A.
B.
C.
D.
12.
正方体为棱长为2,动点,分别在棱,上,过点,,的平面截该正方体所得的截面记为,设,,其中,下列命题正确的是(
)
A.
当时,为矩形,其面积最大为4;
B.
当时,的面积为;
C.
当,时,设与棱的交点为,则;
D.
当时,以为顶点,为底面的棱锥的体积为定值.
三、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.
13.
某校为了普及“一带一路”知识,举行了一次知识竞赛,满分10分,有10名同学代表班级参加比赛,已知学生得分均为整数,比赛结束后统计这10名同学得分情况如折线图所示,则这10名同学成绩的极差为___________,中位数是___________.
14.
已知直角三角形的两直角边长分别为和,则以斜边为轴旋转一周所得几何体的体积为__________.
15.
某汽车站每天均有3辆开往某景点的分为上、中、下等级的客车,某天吴先生准备在该汽车站乘车前往该景点,但他不知道客车的车况,也不知道发车顺序,为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好,则上第二辆,否则上第三辆,那么他乘上上等车的概率为__________.
16.
已知,向量满足,当向量,夹角最大时,__________.
第Ⅱ卷(解答题)
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.
17.
如图,在三棱柱中,侧棱底面,,为的中点,.
(1)求证:平面;
(2)过点作于点,求证:直线平面.
18.
如图,在中,为边上的一点,,,,且与的夹角为.
(Ⅰ),求,的值;
(Ⅱ)的值.
19.
在中,角,,的对边分别是,,,的面积为.现有以下三个条件:①;②;③.请从以上三个条件中选择一个填到下面问题中的横线上,并求解.
已知向量,,函数.在中,,且____________,求的取值范围.
20.
将一颗质地均匀的骰子先后抛掷2次,观察向上的点数,事件:“两数之和为8”,事件:“两数之和是3的倍数”.
(Ⅰ)写出该试验的样本空间,并求事件发生的概率;
(Ⅱ)求事件发生的概率;
(Ⅲ)事件与事件至少有一个发生的概率.
21.
统计某公司1000名推销员的月销售额(单位:千元)得到如下频率分布直方图.
(1)同一组数据用该区间的中间值作代表,求这1000名推销员的月销售额的平均数与方差;
(2)请根据这组数据提出使的推销员能够完成销售指标的建议;
(3)现有两种奖励机制:
方案一:设,销售额落在左侧,每人每月奖励0.4千元;销售额落在内,每人每月奖励0.6千元;销售额落在右侧,每人每月奖励0.8千元.
方案二:每人每月奖励其月销售额的.
用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据:)
记:(其中为对应的频率).
22.
如图,四边形是圆柱的轴截面,点为底面圆周上异于,的点.
(1)求证:平面;
(2)若圆柱的侧面积为,体积为,点为线段上靠近点的三等分点,设,是否存在角使得直线与平面所成角的正弦值最大?若存在,求出相应的正弦值,并求出;若不存在,说明理由.
参考答案
一、选择题:(1-8小题单选,9-12小题多选)
1-5:DBDCD
6-8:CAB
9.
ABC
10.
ACD
11.
AD
12.
BCD
三、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.
13.
7;6
14.
15.
16.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.
17.(1)证明:连接,设,连接,
∵是平行四边形,∴点是的中点,
∵是的中点,∴是的中位线,
∴,
又平面,平面,
∴平面.
(2)∵平面,平面,∴,
又,,
∴直线平面.
解法2:
∵平面,平面,∴平面平面,
又平面平面,,平面,
∴直线平面.
18.(1)如下图,过点作,分别交,点,,
因为,所以,
所以,,
又四边形为平行四边形,所以,
又因为,不共线,所以,.
(2)由(1)知
.
19.
解:.
又.
选择①:,由正弦定理可得:
,故可得,又,
故可得,又,故.
(选择②:,由正弦定理得:
,由余弦定理得,有,故.
选择③:,由面积公式以及余弦定理可得:
,解得,又,故可.
故不论选择哪个条件,都有.)
又.则.
故
,
又,故,
故,故.
20.
解:(Ⅰ)将一颗骰子先后抛掷2次,观察向上的点数,
,共有36个样本点,
它们是等可能的,故这是个古典概型.
,共5个样本点,
∴事件发生的概率为.
(Ⅱ),
共12个样本点.
∴事件发生的概率.
(Ⅲ)事件与事件至少有一个发生,即事件,
,共17个样本点,
∴事件与事件至少有一个发生的概率为.
解法二:因为、不可能同时发生,即、互斥,
所以.
21.(1)由频率分布直方图可得,这1000名推销员的月销售额的平均数为
(万元).
方差为
.
(2)∵,
∴设月销售额为,则,
则,解得,
故根据这组数据可知:将销售指标定为21千元时,才能够使的推销员完成销售指标.
(3)方案一:由(1)可得,,∴,
则当时,,
当时,,
当时,,
1000名推销员的奖励金共计(千元),
方案二:1000名推销员的奖励金(千元),
因为,
所以选择方案一,公司需提供更多的奖励金.
22.
解:(1)证明:因为是圆的直径,点是圆周上一点,
所以,即,
又在圆柱中,母线底面,底面,所以,
又,平面,平面,
所以平面.
(2)设圆柱底面半径为,母线为,则,解得,
在中,过作交于点.
由(1)知平面,因为平面,所以,
又,
所以平面.
若与不重合,即为直线与平面所成的角.
若与重合,直线与平面所成的角为,
设,,
则在中,,
在中,,.
于是
.
当且仅当,即,时,等号成立.
故时,直线与平面所成的角的正弦值最大,最大值为1.
同课章节目录
