2021-2022学年苏科版九年级数学上册第2章对称图形-圆达标检测卷(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册第2章对称图形-圆达标检测卷(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 567.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 00:00:00 | ||
图片预览




文档简介
第2章达标检测卷
一、选择题(每题3分,共24分)
1.若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
A.点P在⊙O外
B.点P在⊙O上
C.点P在⊙O内
D.无法确定
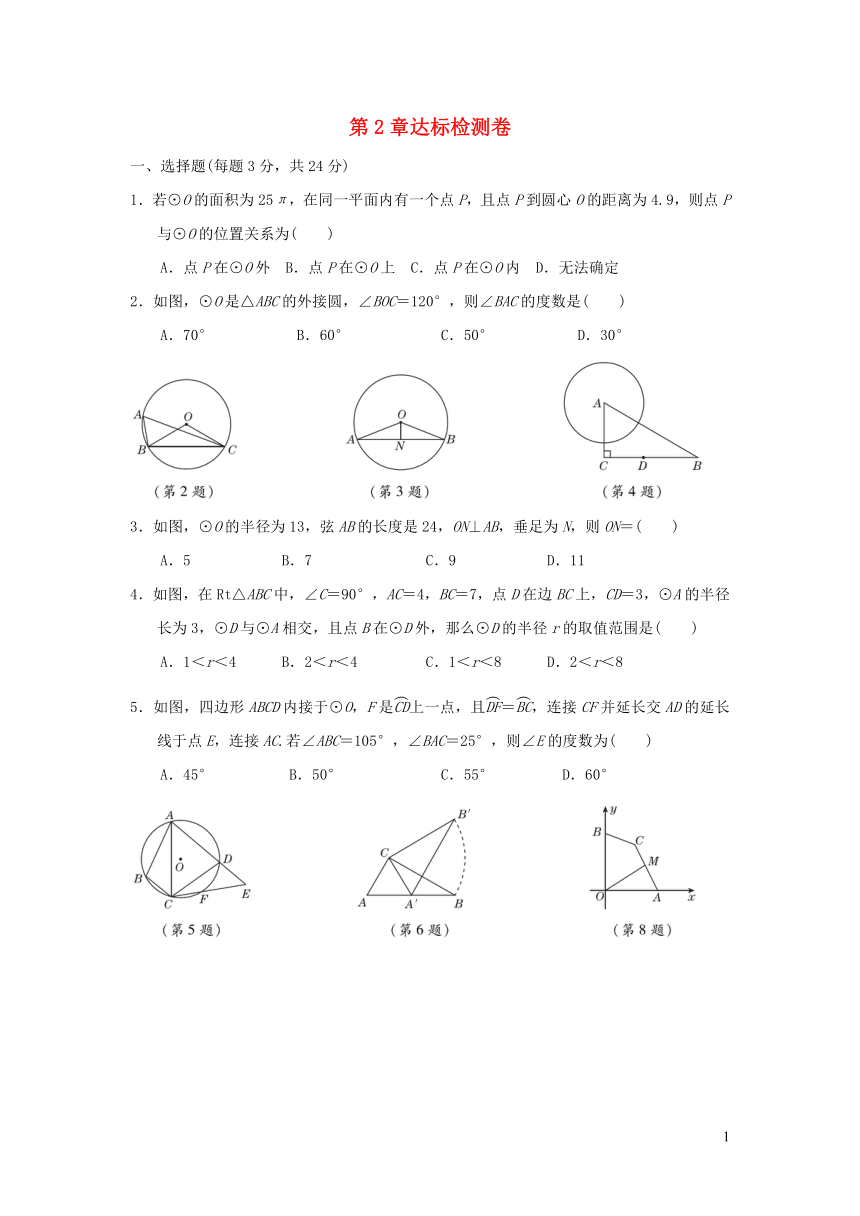
2.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.70°
B.60°
C.50°
D.30°
3.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
4.如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径r的取值范围是( )
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
5.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45°
B.50°
C.55°
D.60°
6.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
7.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
8.如图,点A、B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
二、填空题(每题2分,共20分)
9.如图,在圆内接四边形ABCD中,若∠A、∠B、∠C的度数之比为4:3:5,则∠D的度数是________.
10.如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则的长为________.
11.如图,⊙O中,=,∠BAC=50°,则∠AEC的度数为________.
12.如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A的度数是________.
13.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
14.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.一个圆锥形漏斗,某同学用三角板(部分)测得其高度的尺寸如图所示(单位:cm),则该圆锥形漏斗的侧面积为________cm2.
16.据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆”,如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为________尺.(结果用最简根式表示)
17.如图,AC⊥BC,AC=BC=4,以BC长为直径作半圆,圆心为点O.以点C为圆心,BC长为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是________.
18.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径是7,则GE+FH的最大值是________.
三、解答题(19~22题每题6分,其余每题8分,共56分)
19.如图,AB是⊙O的直径,点C是圆上一点,连接AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,求⊙O的周长.
20.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
21.已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
(1)如图①,求证:AC=CD;
(2)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.
22.“不在同一条直线上的三个点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.
23.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,恰有AB=AC.
(1)求证:AB是⊙O的切线;
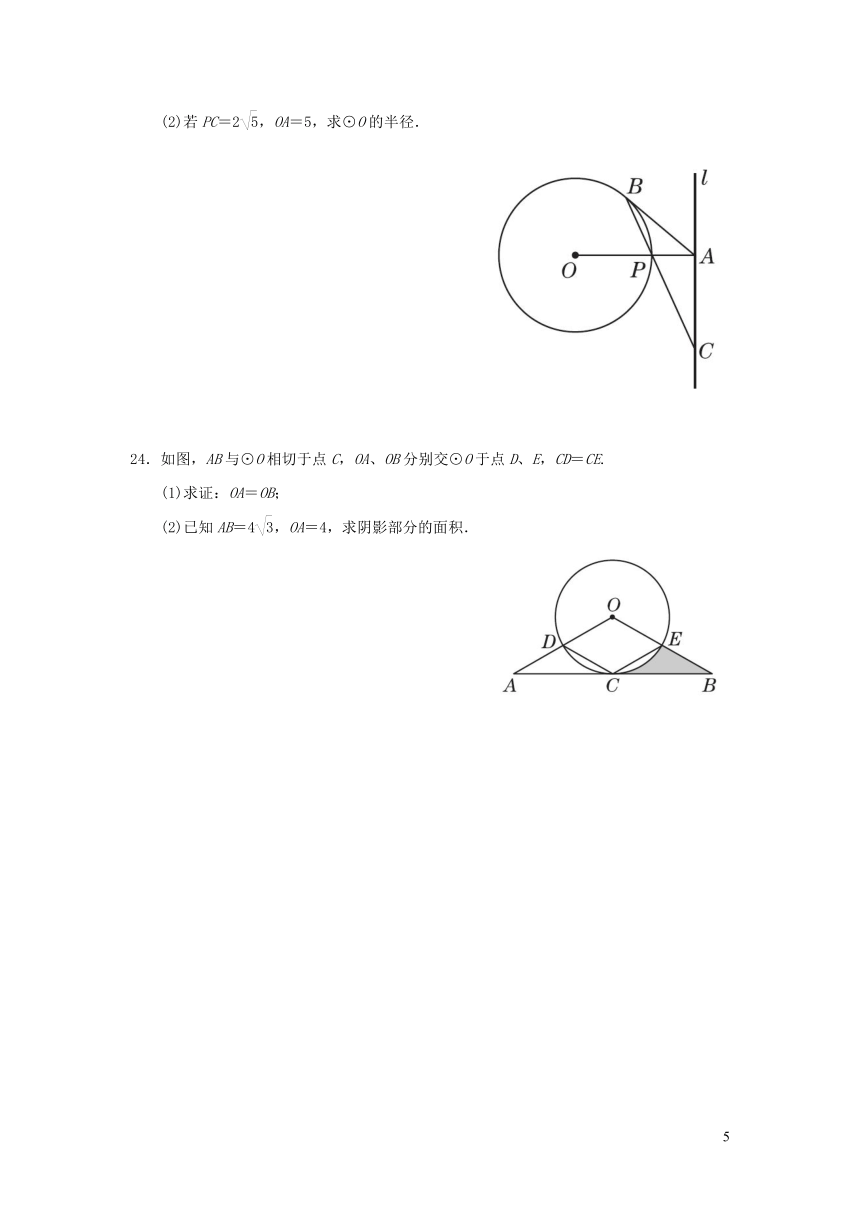
(2)若PC=2,OA=5,求⊙O的半径.
24.如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E,CD=CE.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
25.如图,一座拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径.
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
26.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时,如图①,连接OC,求∠DOC的度数.
(2)当直线CD与半圆O相交时,如图②,设另一交点为E,连接AE,OC,若AE∥OC.
①试猜想AE与OD的数量关系,并说明理由;
②求∠ODC的度数.
答案
一、1.C 2.B 3.A 4.B 5.B
6.B 【点拨】∵∠ACB=90°,∠ABC=30°,AB=2,∴AC=AB=1.∴BC===.∴点B转过的路径长为=.
7.C
8.B 【点拨】如图,∵点C为坐标平面内一点,BC=1,
∴C在以B为圆心,半径为1的圆上,取OD=OA=2,连接CD,
又∵AM=CM,∴OM是△ACD的中位线,∴OM=CD,
当OM最大时,CD最大,而当D,B,C三点共线,且C在DB的延长线上时,CD最大,即OM最大,∵OB=OD=2,∠BOD=90°,∴BD=2,
∴CD=2+1,∴OM=CD=+,即OM的最大值为+.
二、9.120° 10.π 11.65° 12.35°
13.3 【点拨】过点O作OH⊥CD于H,连接OC,则CH=DH=CD=4,
在Rt△OCH中,OH==3,所以CD与AB之间的距离是3.
14.215 【点拨】∵A,B,C,D四点共圆,∴∠B+∠ADC=180°.又∵A,C,D,E四点共圆,∴∠E+∠ACD=180°.∴∠ACD+∠ADC+∠B+∠E=360°.∵∠ACD+∠ADC=180°-35°=145°,∴∠B+∠E=360°-145°=215°.
15.15π
16.4 【点拨】如图,∵四边形CDEF为正方形,∴∠D=90°,CD=DE,∴CE为直径,∠ECD=45°,由题意得AB=2.5,∴CE=2.5-0.25×2=2,
∴CD==,
∴正方形CDEF的周长为4尺.
17.π-2 【点拨】如图,连接CE.∵AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作弧AB,
∴∠ACB=90°,OB=OC=OD=2,BC=CE=4.
又∵OE∥AC,
∴∠COE=90°.
∵OC=2,CE=4,
∴∠CEO=30°,∠ECB=60°,OE=2.
∴S阴影=S扇形CBE-S扇形OBD-S△OCE=-π×22-×2×2=-2.
18.10.5 【点拨】当GH为⊙O的直径时,GE+FH有最大值.易知当GH为直径时,E点与O点重合,∴AC也是直径,AC=14.∵∠ABC是直径上的圆周角,∴∠ABC=90°,∵∠C=30°,∴AB=AC=7.∵点E、F分别为AC、BC的中点,∴EF=AB=3.5,∴GE+FH=GH-EF=14-3.5=10.5.
三、19.解:∵AB是⊙O的直径,∴∠ACB=90°,在Rt△CBD中,∵CD=4,BD=3,∴BC===5.设AD=x,则42+x2=(x+3)2-52,解得x=.
∴AB=+3=,
∴⊙O的周长是π,
20.(1)证明:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,
∵∠BAC=60°,∠ADB=90°,
∴△ABC是等边三角形,∠BAD=30°.
∴∠C=60°.
在Rt△BAD中,∠BAD=30°,AB=8,
∴BD=4,∴DC=4.
∵DE⊥AC,∴∠DEC=90°,
∴∠CDE=30°,∴CE=DC=2.
∴DE==2.
21.(1)证明:
∵直线AC与⊙O相切,
∴OA⊥AC,
∴∠OAC=90°,即∠OAB+∠CAB=90°.
∵OC⊥OB,∴∠BOC=90°,
∴∠B+∠ODB=90°.
而∠ODB=∠ADC,
∴∠ADC+∠B=90°.
∵OA=OB,
∴∠OAB=∠B,
∴∠ADC=∠CAB,∴AC=CD.
(2)解:∵∠BOC=90°,OB=OE,
∴△OBE为等腰直角三角形,
∴∠OEB=45°.
∵BE∥OA,
∴∠AOC=∠OEB=45°,
∴△OAC为等腰直角三角形,
∴AC=OA=1,OC=OA=,
而CD=CA=1,
∴OD=OC-CD=-1.
22.解:设经过A,B两点的直线对应的函数关系式为y=kx+b.
∵A(2,3),B(-3,-7),
∴解得
∴经过A,B两点的直线对应的函数关系式为y=2x-1.
当x=5时,y=2×5-1=9≠11,
∴点C(5,11)不在直线AB上,
即A,B,C三点不在同一条直线上.
∴平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)可以确定一个圆.
23.(1)证明:如图,连接OB.
∵OA⊥l,
∴∠PAC=90°,
∴∠APC+∠ACP=90°.
∵AB=AC,OB=OP,
∴∠ABC=∠ACB,∠OBP=∠OPB.
∵∠BPO=∠APC,
∴∠ABC+∠OBP=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线.
(2)解:设⊙O的半径为r,则AP=5-r,OB=r.
在Rt△OBA中,AB2=OA2-OB2=52-r2,
在Rt△APC中,AC2=PC2-AP2=(2)2-(5-r)2.
∵AB=AC,
∴52-r2=(2)2-(5-r)2,
解得r=3,即⊙O的半径为3.
24.(1)证明:连接OC.
∵AB与⊙O相切于点C,
∴OC⊥AB.∴∠ACO=∠BCO=90°.
∵CD=CE,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC,∴OA=OB.
(2)解:∵△AOC≌△BOC,∴AC=BC=AB=2.
∵OB=OA=4,且△OCB是直角三角形,∴根据勾股定理,得OC==2,∴OC=OB,∴∠B=30°,
∴∠BOC=60°.
∴S阴影=S△BOC-S扇形OCE=×2×2-=2-π.
25.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连接AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设圆E的半径是r米,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2.解得r=50.
∴桥拱的半径为50米.
(2)这艘轮船能顺利通过.理由如下:如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连接EM,
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过.
26.解:(1)∵直线CD与半圆O相切,
∴∠OCD=90°.
∵OC=OA,CD=OA,
∴OC=CD,
∴∠DOC=∠ODC=45°,
即∠DOC的度数是45°.
(2)①AE=OD.
理由如下:
如图,连接OE.
∵OC=OA,CD=OA,
∴OC=CD,
∴∠COD=∠CDO.
∴∠OCE=2∠CDO,
∵AE∥OC,
∴∠EAD=∠COD,
∴∠EAD=∠CDO,
∴AE=DE.
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DOE=2∠EAD,
∴∠DOE=∠OCE.
∵OC=OE,
∴∠DEO=∠OCE,
∴∠DOE=∠DEO,
∴OD=DE,
∴AE=OD.
②由①得,∠DOE=∠DEO=2∠ODC.
∵∠DOE+∠DEO+∠ODC=180°,
∴2∠ODC+2∠ODC+∠ODC=180°,
∴∠ODC=36°.
1
一、选择题(每题3分,共24分)
1.若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
A.点P在⊙O外
B.点P在⊙O上
C.点P在⊙O内
D.无法确定
2.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.70°
B.60°
C.50°
D.30°
3.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
4.如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径r的取值范围是( )
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
5.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45°
B.50°
C.55°
D.60°
6.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
7.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
8.如图,点A、B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
二、填空题(每题2分,共20分)
9.如图,在圆内接四边形ABCD中,若∠A、∠B、∠C的度数之比为4:3:5,则∠D的度数是________.
10.如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则的长为________.
11.如图,⊙O中,=,∠BAC=50°,则∠AEC的度数为________.
12.如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A的度数是________.
13.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
14.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.一个圆锥形漏斗,某同学用三角板(部分)测得其高度的尺寸如图所示(单位:cm),则该圆锥形漏斗的侧面积为________cm2.
16.据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆”,如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为________尺.(结果用最简根式表示)
17.如图,AC⊥BC,AC=BC=4,以BC长为直径作半圆,圆心为点O.以点C为圆心,BC长为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是________.
18.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径是7,则GE+FH的最大值是________.
三、解答题(19~22题每题6分,其余每题8分,共56分)
19.如图,AB是⊙O的直径,点C是圆上一点,连接AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,求⊙O的周长.
20.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
21.已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
(1)如图①,求证:AC=CD;
(2)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.
22.“不在同一条直线上的三个点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.
23.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,恰有AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2,OA=5,求⊙O的半径.
24.如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E,CD=CE.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
25.如图,一座拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径.
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
26.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时,如图①,连接OC,求∠DOC的度数.
(2)当直线CD与半圆O相交时,如图②,设另一交点为E,连接AE,OC,若AE∥OC.
①试猜想AE与OD的数量关系,并说明理由;
②求∠ODC的度数.
答案
一、1.C 2.B 3.A 4.B 5.B
6.B 【点拨】∵∠ACB=90°,∠ABC=30°,AB=2,∴AC=AB=1.∴BC===.∴点B转过的路径长为=.
7.C
8.B 【点拨】如图,∵点C为坐标平面内一点,BC=1,
∴C在以B为圆心,半径为1的圆上,取OD=OA=2,连接CD,
又∵AM=CM,∴OM是△ACD的中位线,∴OM=CD,
当OM最大时,CD最大,而当D,B,C三点共线,且C在DB的延长线上时,CD最大,即OM最大,∵OB=OD=2,∠BOD=90°,∴BD=2,
∴CD=2+1,∴OM=CD=+,即OM的最大值为+.
二、9.120° 10.π 11.65° 12.35°
13.3 【点拨】过点O作OH⊥CD于H,连接OC,则CH=DH=CD=4,
在Rt△OCH中,OH==3,所以CD与AB之间的距离是3.
14.215 【点拨】∵A,B,C,D四点共圆,∴∠B+∠ADC=180°.又∵A,C,D,E四点共圆,∴∠E+∠ACD=180°.∴∠ACD+∠ADC+∠B+∠E=360°.∵∠ACD+∠ADC=180°-35°=145°,∴∠B+∠E=360°-145°=215°.
15.15π
16.4 【点拨】如图,∵四边形CDEF为正方形,∴∠D=90°,CD=DE,∴CE为直径,∠ECD=45°,由题意得AB=2.5,∴CE=2.5-0.25×2=2,
∴CD==,
∴正方形CDEF的周长为4尺.
17.π-2 【点拨】如图,连接CE.∵AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作弧AB,
∴∠ACB=90°,OB=OC=OD=2,BC=CE=4.
又∵OE∥AC,
∴∠COE=90°.
∵OC=2,CE=4,
∴∠CEO=30°,∠ECB=60°,OE=2.
∴S阴影=S扇形CBE-S扇形OBD-S△OCE=-π×22-×2×2=-2.
18.10.5 【点拨】当GH为⊙O的直径时,GE+FH有最大值.易知当GH为直径时,E点与O点重合,∴AC也是直径,AC=14.∵∠ABC是直径上的圆周角,∴∠ABC=90°,∵∠C=30°,∴AB=AC=7.∵点E、F分别为AC、BC的中点,∴EF=AB=3.5,∴GE+FH=GH-EF=14-3.5=10.5.
三、19.解:∵AB是⊙O的直径,∴∠ACB=90°,在Rt△CBD中,∵CD=4,BD=3,∴BC===5.设AD=x,则42+x2=(x+3)2-52,解得x=.
∴AB=+3=,
∴⊙O的周长是π,
20.(1)证明:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,
∵∠BAC=60°,∠ADB=90°,
∴△ABC是等边三角形,∠BAD=30°.
∴∠C=60°.
在Rt△BAD中,∠BAD=30°,AB=8,
∴BD=4,∴DC=4.
∵DE⊥AC,∴∠DEC=90°,
∴∠CDE=30°,∴CE=DC=2.
∴DE==2.
21.(1)证明:
∵直线AC与⊙O相切,
∴OA⊥AC,
∴∠OAC=90°,即∠OAB+∠CAB=90°.
∵OC⊥OB,∴∠BOC=90°,
∴∠B+∠ODB=90°.
而∠ODB=∠ADC,
∴∠ADC+∠B=90°.
∵OA=OB,
∴∠OAB=∠B,
∴∠ADC=∠CAB,∴AC=CD.
(2)解:∵∠BOC=90°,OB=OE,
∴△OBE为等腰直角三角形,
∴∠OEB=45°.
∵BE∥OA,
∴∠AOC=∠OEB=45°,
∴△OAC为等腰直角三角形,
∴AC=OA=1,OC=OA=,
而CD=CA=1,
∴OD=OC-CD=-1.
22.解:设经过A,B两点的直线对应的函数关系式为y=kx+b.
∵A(2,3),B(-3,-7),
∴解得
∴经过A,B两点的直线对应的函数关系式为y=2x-1.
当x=5时,y=2×5-1=9≠11,
∴点C(5,11)不在直线AB上,
即A,B,C三点不在同一条直线上.
∴平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)可以确定一个圆.
23.(1)证明:如图,连接OB.
∵OA⊥l,
∴∠PAC=90°,
∴∠APC+∠ACP=90°.
∵AB=AC,OB=OP,
∴∠ABC=∠ACB,∠OBP=∠OPB.
∵∠BPO=∠APC,
∴∠ABC+∠OBP=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线.
(2)解:设⊙O的半径为r,则AP=5-r,OB=r.
在Rt△OBA中,AB2=OA2-OB2=52-r2,
在Rt△APC中,AC2=PC2-AP2=(2)2-(5-r)2.
∵AB=AC,
∴52-r2=(2)2-(5-r)2,
解得r=3,即⊙O的半径为3.
24.(1)证明:连接OC.
∵AB与⊙O相切于点C,
∴OC⊥AB.∴∠ACO=∠BCO=90°.
∵CD=CE,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC,∴OA=OB.
(2)解:∵△AOC≌△BOC,∴AC=BC=AB=2.
∵OB=OA=4,且△OCB是直角三角形,∴根据勾股定理,得OC==2,∴OC=OB,∴∠B=30°,
∴∠BOC=60°.
∴S阴影=S△BOC-S扇形OCE=×2×2-=2-π.
25.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连接AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设圆E的半径是r米,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2.解得r=50.
∴桥拱的半径为50米.
(2)这艘轮船能顺利通过.理由如下:如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连接EM,
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过.
26.解:(1)∵直线CD与半圆O相切,
∴∠OCD=90°.
∵OC=OA,CD=OA,
∴OC=CD,
∴∠DOC=∠ODC=45°,
即∠DOC的度数是45°.
(2)①AE=OD.
理由如下:
如图,连接OE.
∵OC=OA,CD=OA,
∴OC=CD,
∴∠COD=∠CDO.
∴∠OCE=2∠CDO,
∵AE∥OC,
∴∠EAD=∠COD,
∴∠EAD=∠CDO,
∴AE=DE.
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DOE=2∠EAD,
∴∠DOE=∠OCE.
∵OC=OE,
∴∠DEO=∠OCE,
∴∠DOE=∠DEO,
∴OD=DE,
∴AE=OD.
②由①得,∠DOE=∠DEO=2∠ODC.
∵∠DOE+∠DEO+∠ODC=180°,
∴2∠ODC+2∠ODC+∠ODC=180°,
∴∠ODC=36°.
1
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
