（沪教版）二年级数学上册教案 幻方 1

数学广场——幻方
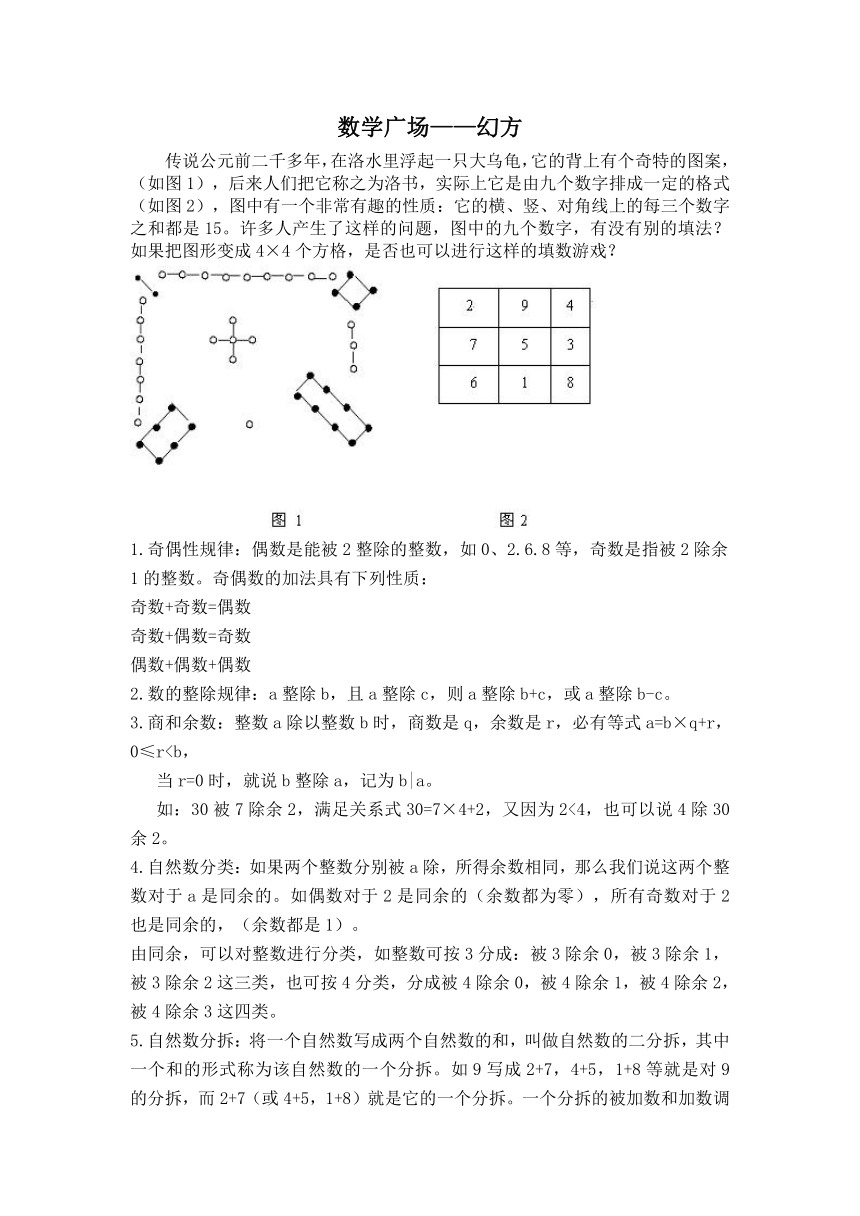
传说公元前二千多年，在洛水里浮起一只大乌龟，它的背上有个奇特的图案，（如图1），后来人们把它称之为洛书，实际上它是由九个数字排成一定的格式（如图2），图中有一个非常有趣的性质：它的横、竖、对角线上的每三个数字之和都是15。许多人产生了这样的问题，图中的九个数字，有没有别的填法？如果把图形变成4×4个方格，是否也可以进行这样的填数游戏？
1.奇偶性规律：偶数是能被2整除的整数，如0、2.6.8等，奇数是指被2除余1的整数。奇偶数的加法具有下列性质：
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数+偶数
2.数的整除规律：a整除b，且a整除c，则a整除b+c，或a整除b-c。
3.商和余数：整数a除以整数b时，商数是q，余数是r，必有等式a=b×q+r，0≤r当r=0时，就说b整除a，记为b|a。
如：30被7除余2，满足关系式30=7×4+2，又因为2<4，也可以说4除30余2。
4.自然数分类：如果两个整数分别被a除，所得余数相同，那么我们说这两个整数对于a是同余的。如偶数对于2是同余的（余数都为零），所有奇数对于2也是同余的，（余数都是1）。
由同余，可以对整数进行分类，如整数可按3分成：被3除余0，被3除余1，被3除余2这三类，也可按4分类，分成被4除余0，被4除余1，被4除余2，被4除余3这四类。
5.自然数分拆：将一个自然数写成两个自然数的和，叫做自然数的二分拆，其中一个和的形式称为该自然数的一个分拆。如9写成2+7，4+5，1+8等就是对9的分拆，而2+7（或4+5，1+8）就是它的一个分拆。一个分拆的被加数和加数调换位置后得到的分拆视为同一个分拆，如2+7和7+2视为9的同一分拆。
例1：将1-9这九个数，填入图3的方格内，使每行、每列、及两条对角线上三个数字的和都相等。
分析与解：假设图形中填入的数如图4所示，并设各边和对角线的三数之和为k，则解法的关键是找出中心数及各顶点的数。我们分三步来完成：
（1）求每行、每列三个数的和，即k值。
（2）确定中心数，即b2=？
（3）试填各顶点数及其它方格内数。
∵a1+b1+c1+a2+b2+c2+a3+b3+c3=3k
又∵a1+b1+c1+a2+b2+c2+a3+b3+c3=1+2+…+9=45
∴3k=45 k=15
∵a1+b2+c3=a2+b2+c2=a3+b2+c1=b1+b2+b3=15
∴(a1+b2+c3)+(a2+b2+c2)+(a3+b2+c1)+(b1+b2+b3)=4×15
(a1+a2+a3+b1+b2+b3+c1+c2+c3)+3b2=60
45+3b2=60 3b2=15 b2=5
试填a1，若a1为奇，∵a1+c3=10，故C3为奇，a2和a3也应同奇或同偶，若a2.a3同奇，则c2为奇，b3为奇，这样就出现了六个奇数，与1-9的自然数中只有5个奇数矛盾；若a2和a3同偶，则c2为偶，b3为偶，c1也为偶，这样共出现了五个偶数，与1-9的自然数中只有4个偶数矛盾，故a1不能为奇数，则a1应填偶数，此时c1.a3.c3也只能取偶数，由于a1+c3=C1+a3=10，又∵2+8=4+6=10，故只需取a1=2，C3=8，a3=4，c1=6即可，其它各方格中的数须填a2=9，b2=3。C2=1，b1=7。如图5所示，这样就得到本题的一个解，若取a1=4，c3=6，a3=2，c1=8，须取a2=9，b3=7，b1=3，c2=1，根据对称轮换，答案是唯一的。
说明：此题是引例中的问题，将1-9九个数，填入列3×3个方格内，使每行每列、每条对角线的和相等，这叫做三阶幻方，一般地，在n×n个方格内，填上n×n个连续自然数，并且每行、每列、每条对角线上n个自然数的和都相等，则称它为n阶幻方。解决幻方问题的关键是确定中心数和顶点数。
例2：把1到6这六个数分别填在图7-a中三角形三条边上的六个圆圈内，使每条边上三个圆圈内的数的和都相等。
分析与解：设填入顶点圆圈内的数分别为a、b、c，其余三个圆圈内的数分别是d、e、f。每条边上三个圆圈内数的和为k，如图7-a。
∵a+d+b=k,b+e+c=k,a+f+c=k
∴(a+d+b)+(b+e+c)+(a+b+c)=3k
又∵a+b+c+d+e+f=1+2+…+6=21
∴(a+b+c+d+e+f)+(a+b+c)=3k
21+(a+b+c)=3k
由上式可知：a+b+c最小时，k值也最小，a+b+c最大时，k值也最大，且k是整数，当a+b+c=1+2+3=6时，k=9，a+b+c=4+5+6=15时，k=12，所以k可取9、10、11.12四种情况。
当k=9时，a+b+c=6，6只有一个三拆分，6=1+2+3，因此a=1，b=2，c=3，其余三个圆圈内分别填4.5.6.，即e=4，f=5，d=6。这样就得到一个基本解（如图8）将这个解左、右旋转或适当调换后，可以得到其余的五个解。
当k=10时，a+b+c=9，9有三种三拆分，9=1+2+6=1+3+5=2+3+4，当a、b、C为1，2，6时，以2.6为顶点的一边只能填2，如图9-a，2重复了，故此解排除；当a、b、C为1.3.5时，其余边上的圆圈内约数填上2.4.6即可（如图9-b）；当a、b、c为2.3.4时，以3.4为顶点的一边只能填上3，如图9-c，3重复了，故此解也排除。
当k=11，12时，可仿照上面方法求出基本解。
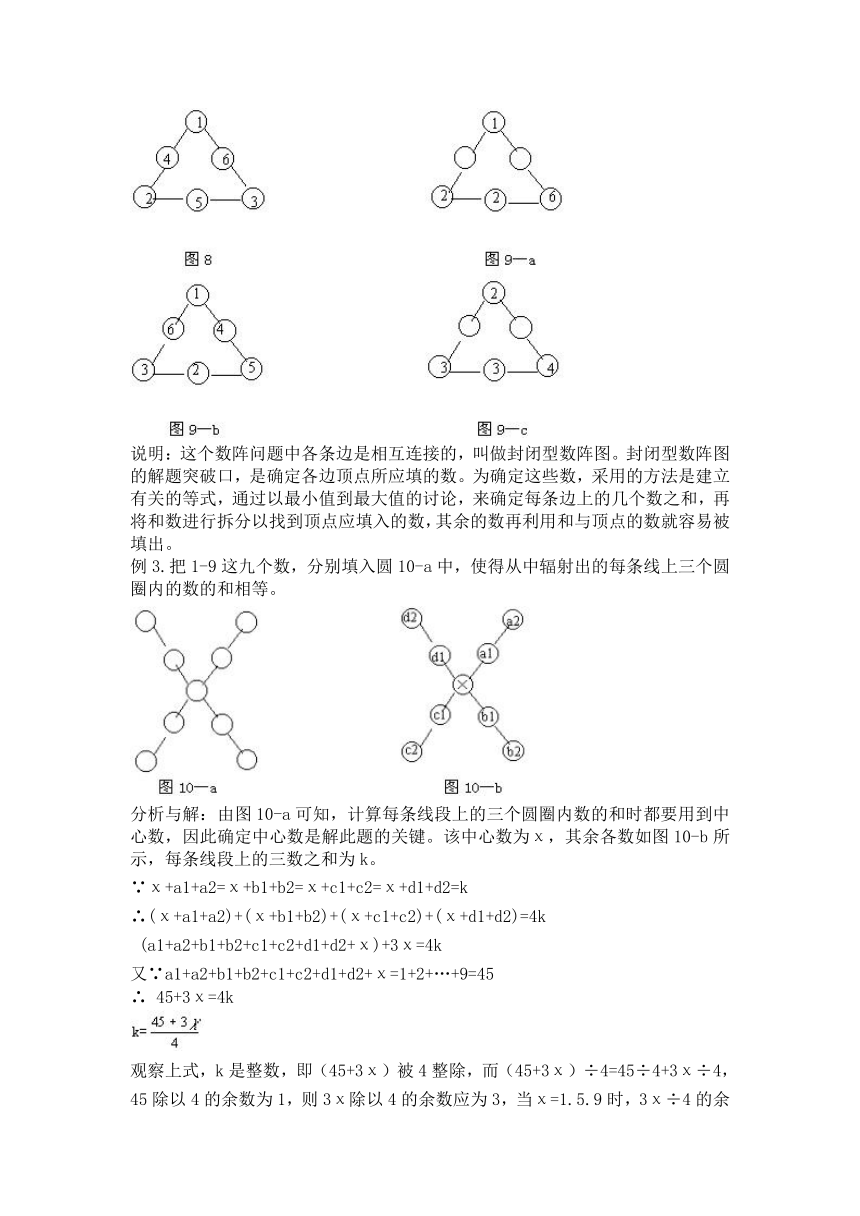
说明：这个数阵问题中各条边是相互连接的，叫做封闭型数阵图。封闭型数阵图的解题突破口，是确定各边顶点所应填的数。为确定这些数，采用的方法是建立有关的等式，通过以最小值到最大值的讨论，来确定每条边上的几个数之和，再将和数进行拆分以找到顶点应填入的数，其余的数再利用和与顶点的数就容易被填出。
例3.把1-9这九个数，分别填入圆10-a中，使得从中辐射出的每条线上三个圆圈内的数的和相等。
分析与解：由图10-a可知，计算每条线段上的三个圆圈内数的和时都要用到中心数，因此确定中心数是解此题的关键。该中心数为χ，其余各数如图10-b所示，每条线段上的三数之和为k。
∵χ+a1+a2=χ+b1+b2=χ+c1+c2=χ+d1+d2=k
∴(χ+a1+a2)+(χ+b1+b2)+(χ+c1+c2)+(χ+d1+d2)=4k
(a1+a2+b1+b2+c1+c2+d1+d2+χ)+3χ=4k
又∵a1+a2+b1+b2+c1+c2+d1+d2+χ=1+2+…+9=45
∴ 45+3χ=4k
观察上式，k是整数，即（45+3χ）被4整除，而（45+3χ）÷4=45÷4+3χ÷4，45除以4的余数为1，则3χ除以4的余数应为3，当χ=1.5.9时，3χ÷4的余数为3。
当χ=1时，k=（45+3×1）÷4=12，12拆分成含有一个1的三个自然数的和有以下四种形式：
12=1+2+9=1+3+8=1+4+7=1+5+6这样就得到一个解（如图11-a）。
当χ=5.9时，仿照上面方法可得到相应的解，（如图11-b，图11-c所示）。
说明：此题中的数阵图，称为辐射型数阵图，解法的关键是确定中心数。具体方法是：通过所给条件建立有关等式，通过整除性的讨论，确定出中心数的取值，然后求出各边上数的和，最后将和自然数分拆成中心数的若干个自然数之和，确定边上其他的数。
例4.，如图12-a中，以○为顶点，有四个小的等腰三角形和三个大的等腰三解形，将1-9这九个数，填入○内，使每个三角形的三个顶点的数字之和相等。
分析与解：设应填入的数如图12-b所示，观察可知，在计算每个小三角形和大三角形各顶点数字和时，最中间的小三角形三个顶点分别用了三次，其中各顶点用了二次，设每个三角形的三个顶点数的和为k，即：
a+b+c=k,d+e+f=k,c+e+g=k,g+h+I=k
a+g+d=k,b+e+h=k,c+f+I=k
∵(a+b+c)+(d+e+f)+(c+e+g)+(g+h+i)+(a+g+d)+(b+e+h)+(c+f+i)=7k
即：（a+b+c+d+e+f+g+h+i）+(c+e+g)=7k
a+b+c+d+e+f+g+h+I=3k
又∵a+b+c+d+e+f+g+h+I=1+2+…+9=45
∴ 3k=45
k=15
在1-9这九个数中，15的三拆分有下列几种情况：
15=1+9+5=1+8+6=2+9+4=2+8+5=3+7+5=2+7+6=3+8+4=4+5+6，在这些拆分中，2.4.5.6.8、出现过三次，其它数字出现过两次，所以C=2，e=8，g=5或c=6，e=4，g=5，再将其它数填入，这样就得到本题的两个解（如图13-a，图13-b所示）
说明：此题中的数阵图为复合型数阵图，解题的关键是要以中心数和顶点数为突破口。
及时练习：
1.用九个连续自然数构造一个三阶幻方，使每一横行及每一竖列的三个数之和都等于60。
2.将1-9这九个自然数分别填入如图14的九个○内，使三角形每边上的四数之和都等于19，且有一个顶点○的数字为1。
3.将1-7这七个数字填写到如图15的小圆圈中，使每条直径上的三个数字之和都为10。
4.把1-10这十个数分别填在如图16的五边形边上的十个圆圈内，使每条边上的三个圆圈内的数的和尽可能最小。
5.把1-9这九个数分别填入如图17的大三角形中的九个小三角形内（每个小三角形只填一个数），要求靠近大三角形三条边的每五个数相加的和相等，问怎样填才能使五个数的和尽可能地大一些，这五个数的和的最大值是多少？
答案：1.解：先用1-9这九个自然数构造一个三阶幻方（如图18-a），这个三阶幻方的每行，每列之和为15，题目要求和为60，只需将每个数都加上15即可（如图18-b）
2.设三个顶点数字之和为m，每边三个数之和为k，由于顶点的数属于两边公有，所以将三条边的数字和加在一起，等于将1-9加了一遍，同时将三个顶点数多加了一遍，因为1-9九个自然数的和为45，故m+45=3k， ，由题目可知k=19，∴m=12，将12三拆分且含有1的结果是12=1+2+9=1+3+8=1+4+7=1+5+6，排除1.2.9，1.3.8，1.5.6，填入1.4.7。再填入其它各数。即得解（如图19）
3.解：设每条直径的三个数字之和为k，将所有直径的数字相加，中心数加了三次，其它各数加了一次，设中心数为χ，则
(1+2+…+7)+2χ=3k
28+2χ=3k
由题目可知k=10，则χ=1，再填出其它各数。如图20所示。
4.解：设各顶点数之和为m，五边形每条边上的数字和为k，将五条边的所有数字相加时，各顶点数加了两次，其余各数加了一次，则
（1+2+3+…10）+m=5k
55+m=5k
当m=1+2+3+4+5=15时，k值最小，k=14，将1.2.3.4.5分别填入各个顶点，再由k=14填出其余各数，如图21所示：
5解：设填入的数为a、b、c、d、e、f、g、h、I靠近大三角形边的五个数相加的和是k，由图22-a可知：
a+c+b+f+e=k
e+f+g+g+I=k
a+c+d+h+I=k
∴2(a+b+c+d+e+f+g+h+i)-(b+d+g)=3k
90-(b+d+g)=3k
要使k最大，使b+d+g的值最小，分别取b、d、g为1.2.3，求得k=28，再填入其余各数，如图22-b。