2021-2022学年七年级数学上册 华东师大版4.4平面图形-同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年七年级数学上册 华东师大版4.4平面图形-同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 14:08:54 | ||
图片预览



文档简介
2021-2022学年七年级数学上册(华东师大版)
4.4平面图形-同步练习
时间:60分钟
一、单选题
1.下面几种几何图形中,属于平面图形的是(
)
①三角形
②长方形
③正方体
④圆
⑤四棱锥
⑥圆柱
A.①②④
B.①②③
C.①②⑥
D.④⑤⑥
2.图中的小猫(示意图)是由三角形组成的,三角形的个数为( )
A.6
B.8
C.10
D.11
3.如图所示的美丽图案是由我们所熟悉的哪些图形组成的( )
A.三角形和半圆
B.圆和四边形
C.圆和三角形
D.半圆和四边形
4.下列各组图形都是平面图形的一组是(
)
A.线段、圆、圆锥、球
B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球
D.圆、三角形、正方形、长方形
5.用一个平面去截四棱柱,截面的形状不可能为(
)
A.四边形
B.五边形
C.六边形
D.七边形
6.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
7.下列几何图形:①三角形;②长方形;③正方体;④圆;⑤球;⑥正方形.其中平面图形有(
)
A.1个
B.2个
C.3个
D.4个
8.组成如图的美丽图案的是(
)
A.三角形和扇形
B.圆和四边形
C.圆和三角形
D.圆和扇形
二、填空题
9.如图,一个的长方形可以用2种不同的方式分割成3或6个小正方形,那么一个的长方形用不同的方式分割后,小正方形的个数可以是________.
或?
10.下面有一张大图,这张大图的右下方有一块空白,是要填空的.填什么___,请看大图右方若干个标有数码的小图.它们的大小、形状与右下角空白处一样.请将你要填的图的数码号写入空白处,使大图成为一张图形完整、协调一致的图.
11.在如图的四个图形中,是平面图形的有______(请填序号).
12.如图是小明同学为班级报刊《学习园地》设计的图案,则图中的平面图形有________、________、________.(至少写出三种)
13.几何图形中,像直线、角、三角形、圆等,它们上面的各点都在____平面内,这样的图形叫做____.
14.如图所示,图中共有___个长方形.
15.如图,已知五角星的面积为5,正方形的面积为4,图中对应阴影部分的面积分别是S1,S2,则S1-S2的值为_____.
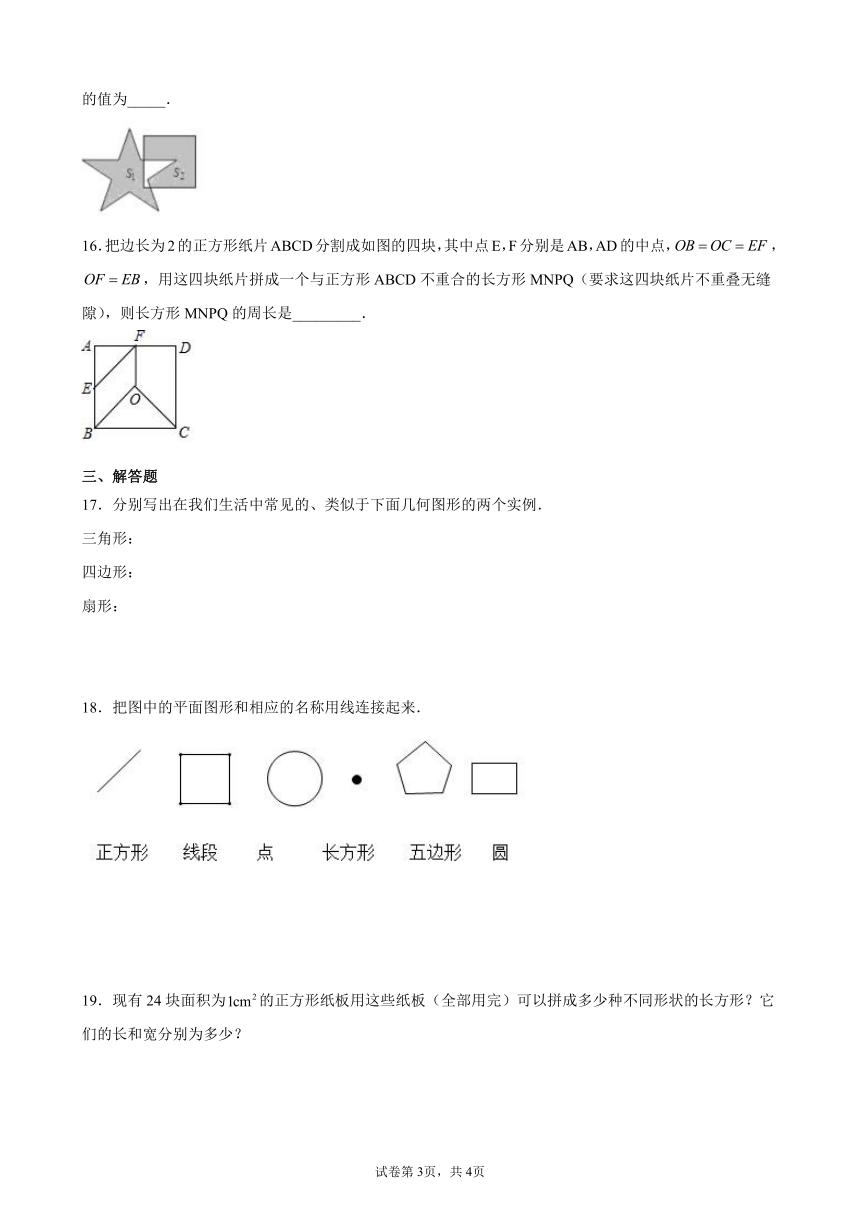
16.把边长为2的正方形纸片ABCD分割成如图的四块,其中点E,F分别是AB,AD的中点,,,用这四块纸片拼成一个与正方形ABCD不重合的长方形MNPQ(要求这四块纸片不重叠无缝隙),则长方形MNPQ的周长是_________.
三、解答题
17.分别写出在我们生活中常见的、类似于下面几何图形的两个实例.
三角形:
四边形:
扇形:
18.把图中的平面图形和相应的名称用线连接起来.
19.现有24块面积为的正方形纸板用这些纸板(全部用完)可以拼成多少种不同形状的长方形?它们的长和宽分别为多少?
20.现有两块可以重叠的三角板,在相等长的两边重合时,能拼出多少种不同的三角形?画图说明.
21.一个六棱柱模型如所示,它的底面边长都是6cm,侧棱长4cm,观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面的面积之和是多少?
22.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】在①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱等几何图形中,属于平面图形的是:三角形、长方形、圆;属于立体图形的是:正方体、四棱锥和圆柱.
∴属于平面图形的是:①②④.
故选A.
2.D
【解析】由图可知,小猫图案中共有11个三角形.
故选D.
3.A
【解析】解:观察图案可知,这个美丽的图案是由半圆和三角形组成,
故选:A.
4.D
【解析】解:A.圆锥、球是立体图形,不是平面图形,故此选项错误;
B.圆柱是立体图形,不是平面图形,故此选项错误;
C.长方体、圆柱、棱锥、球都是立体图形,不是平面图形,故此选项错误;
D.圆、三角形、正方形、长方形都是平面图形,故此选项正确.
故选D.
5.D
【解析】用平面去截四棱柱时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
6.C
【解析】A.圆锥和球不是平面图形,故错误;
B.
棱锥、棱柱不是平面图形,故错误;
C.角,三角形,正方形,圆都是平面图形,故正确;
D.长方体不是平面图形,故错误.
故选C.
7.D
【解析】解:①三角形;②长方形;④圆;⑥正方形,它们的各部分都在同一个平面内,属于平面图形;③正方体;⑤球;属于立体图形.
故选D.
8.A
【解析】解:图案是由4个三角形和4个扇形拼接而成的,
故选:A.
9.2个或5个或8个
【解析】因为,
所以的长方形可以分成小正方形的个数可以是2个或个或8个,如图所示:
或或
故答案为:2个或5个或8个.
10.8
【解析】观察得知,每一行的图形是一样的,第三行的图案均应该是三个圆圈,与8中的图案一样,
故答案为:8.
11.①④
【解析】解:①④是平面图形,②③是立体几何,
故答案为①④.
12.圆
三角形
正方形(答案不唯一)
【解析】解:观察图形可知:图中平面图形有圆、三角形、正方形、线段等.
故答案为:圆,三角形,正方形.
13.同一
平面图形
【解析】几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一平面内,那么这样的几何图形叫做平面图形.
故答案为:同一;平面图形.
14.10
【解析】解:长方形是由线段构成,竖向都只有一条线段,横向线段AE上有5个分点(包括端点),每两点有一线段,有一线段得一个长方形,有几条线段就有几个长方形,
所以,长的一边AE上不同的线段共有1+2+3+4=10(条).
所以共有长方形10个.
故答案为:10.
15.1
【解析】设空白部分面积为S
则:S1﹣S2==五角星面积-正方形面积
∵正五角星的面积为
5,正方形的为4
∴S1﹣S2=5-4=1
故答案为1.
16.10
【解析】∵点E,F分别是AB,AD的中点,,
∴如下图,将三角形和四边形移动位置,即可得到长方形MNPQ;
∵正方形纸片ABCD边长为2
结合题意,得,
∴
∴长方形MNPQ的周长
故答案为:10.
17.三角形:三角板、瓦房的人字架.四边形:教室中的黑板面、学生用的书桌面.扇形:学生用的量角器、展开的扇子面.
【解析】解:三角形:三角板、瓦房的人字架.
四边形:教室中的黑板面、学生用的书桌面.
扇形:学生用的量角器、展开的扇子面.
18.见解析
【解析】
19.4种
长宽分别为24和1
12和2
8和3
6和4
【解析】解:能拼成四种,长宽分别为:
(1)241
(2)122
(3)
83
(4)64
20.见解析
【解析】解:如图所示:
从整体看两个直角三角形拼成的图形是两种等腰三角形
从部分看拼成①是直角三角形,②是钝角三角形,③是锐角三角形三类
21.(1)2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;;(2)144cm2
【解析】(1)这个六棱柱有8个面,其中2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;
(2)解法一:其侧面积=六棱柱正视图面积×3
六棱柱正视图是三个长方形组成的大长方形,长为12cm,宽为4cm
六棱柱正视图的面积为12×4=48cm2
其侧面积=六棱柱正视图面积×3=48×3=144cm2.
答:这个六棱柱的所有侧面的面积之和为144cm2.
解法二:其侧面积为:6×4×6=144(m2).
答:这个六棱柱的所有侧面的面积之和为144cm2.
22.(1)π,2π,π;(2)两个月牙形的面积之和等于三角形ABC的面积,理由见解析
【解析】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
设四个月牙的面积依次为S1,S2,S3,S4,如图,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径
SAB为直径=S2+S4+S△ABC,
又由(1)可得:∴SAB为直径=SAC为直径+SBC为直径=π,
S1+S2+S3+S4=S2+S4+S△ABC
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
答案第1页,共2页
答案第1页,共2页
4.4平面图形-同步练习
时间:60分钟
一、单选题
1.下面几种几何图形中,属于平面图形的是(
)
①三角形
②长方形
③正方体
④圆
⑤四棱锥
⑥圆柱
A.①②④
B.①②③
C.①②⑥
D.④⑤⑥
2.图中的小猫(示意图)是由三角形组成的,三角形的个数为( )
A.6
B.8
C.10
D.11
3.如图所示的美丽图案是由我们所熟悉的哪些图形组成的( )
A.三角形和半圆
B.圆和四边形
C.圆和三角形
D.半圆和四边形
4.下列各组图形都是平面图形的一组是(
)
A.线段、圆、圆锥、球
B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球
D.圆、三角形、正方形、长方形
5.用一个平面去截四棱柱,截面的形状不可能为(
)
A.四边形
B.五边形
C.六边形
D.七边形
6.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
7.下列几何图形:①三角形;②长方形;③正方体;④圆;⑤球;⑥正方形.其中平面图形有(
)
A.1个
B.2个
C.3个
D.4个
8.组成如图的美丽图案的是(
)
A.三角形和扇形
B.圆和四边形
C.圆和三角形
D.圆和扇形
二、填空题
9.如图,一个的长方形可以用2种不同的方式分割成3或6个小正方形,那么一个的长方形用不同的方式分割后,小正方形的个数可以是________.
或?
10.下面有一张大图,这张大图的右下方有一块空白,是要填空的.填什么___,请看大图右方若干个标有数码的小图.它们的大小、形状与右下角空白处一样.请将你要填的图的数码号写入空白处,使大图成为一张图形完整、协调一致的图.
11.在如图的四个图形中,是平面图形的有______(请填序号).
12.如图是小明同学为班级报刊《学习园地》设计的图案,则图中的平面图形有________、________、________.(至少写出三种)
13.几何图形中,像直线、角、三角形、圆等,它们上面的各点都在____平面内,这样的图形叫做____.
14.如图所示,图中共有___个长方形.
15.如图,已知五角星的面积为5,正方形的面积为4,图中对应阴影部分的面积分别是S1,S2,则S1-S2的值为_____.
16.把边长为2的正方形纸片ABCD分割成如图的四块,其中点E,F分别是AB,AD的中点,,,用这四块纸片拼成一个与正方形ABCD不重合的长方形MNPQ(要求这四块纸片不重叠无缝隙),则长方形MNPQ的周长是_________.
三、解答题
17.分别写出在我们生活中常见的、类似于下面几何图形的两个实例.
三角形:
四边形:
扇形:
18.把图中的平面图形和相应的名称用线连接起来.
19.现有24块面积为的正方形纸板用这些纸板(全部用完)可以拼成多少种不同形状的长方形?它们的长和宽分别为多少?
20.现有两块可以重叠的三角板,在相等长的两边重合时,能拼出多少种不同的三角形?画图说明.
21.一个六棱柱模型如所示,它的底面边长都是6cm,侧棱长4cm,观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面的面积之和是多少?
22.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】在①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱等几何图形中,属于平面图形的是:三角形、长方形、圆;属于立体图形的是:正方体、四棱锥和圆柱.
∴属于平面图形的是:①②④.
故选A.
2.D
【解析】由图可知,小猫图案中共有11个三角形.
故选D.
3.A
【解析】解:观察图案可知,这个美丽的图案是由半圆和三角形组成,
故选:A.
4.D
【解析】解:A.圆锥、球是立体图形,不是平面图形,故此选项错误;
B.圆柱是立体图形,不是平面图形,故此选项错误;
C.长方体、圆柱、棱锥、球都是立体图形,不是平面图形,故此选项错误;
D.圆、三角形、正方形、长方形都是平面图形,故此选项正确.
故选D.
5.D
【解析】用平面去截四棱柱时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
6.C
【解析】A.圆锥和球不是平面图形,故错误;
B.
棱锥、棱柱不是平面图形,故错误;
C.角,三角形,正方形,圆都是平面图形,故正确;
D.长方体不是平面图形,故错误.
故选C.
7.D
【解析】解:①三角形;②长方形;④圆;⑥正方形,它们的各部分都在同一个平面内,属于平面图形;③正方体;⑤球;属于立体图形.
故选D.
8.A
【解析】解:图案是由4个三角形和4个扇形拼接而成的,
故选:A.
9.2个或5个或8个
【解析】因为,
所以的长方形可以分成小正方形的个数可以是2个或个或8个,如图所示:
或或
故答案为:2个或5个或8个.
10.8
【解析】观察得知,每一行的图形是一样的,第三行的图案均应该是三个圆圈,与8中的图案一样,
故答案为:8.
11.①④
【解析】解:①④是平面图形,②③是立体几何,
故答案为①④.
12.圆
三角形
正方形(答案不唯一)
【解析】解:观察图形可知:图中平面图形有圆、三角形、正方形、线段等.
故答案为:圆,三角形,正方形.
13.同一
平面图形
【解析】几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一平面内,那么这样的几何图形叫做平面图形.
故答案为:同一;平面图形.
14.10
【解析】解:长方形是由线段构成,竖向都只有一条线段,横向线段AE上有5个分点(包括端点),每两点有一线段,有一线段得一个长方形,有几条线段就有几个长方形,
所以,长的一边AE上不同的线段共有1+2+3+4=10(条).
所以共有长方形10个.
故答案为:10.
15.1
【解析】设空白部分面积为S
则:S1﹣S2==五角星面积-正方形面积
∵正五角星的面积为
5,正方形的为4
∴S1﹣S2=5-4=1
故答案为1.
16.10
【解析】∵点E,F分别是AB,AD的中点,,
∴如下图,将三角形和四边形移动位置,即可得到长方形MNPQ;
∵正方形纸片ABCD边长为2
结合题意,得,
∴
∴长方形MNPQ的周长
故答案为:10.
17.三角形:三角板、瓦房的人字架.四边形:教室中的黑板面、学生用的书桌面.扇形:学生用的量角器、展开的扇子面.
【解析】解:三角形:三角板、瓦房的人字架.
四边形:教室中的黑板面、学生用的书桌面.
扇形:学生用的量角器、展开的扇子面.
18.见解析
【解析】
19.4种
长宽分别为24和1
12和2
8和3
6和4
【解析】解:能拼成四种,长宽分别为:
(1)241
(2)122
(3)
83
(4)64
20.见解析
【解析】解:如图所示:
从整体看两个直角三角形拼成的图形是两种等腰三角形
从部分看拼成①是直角三角形,②是钝角三角形,③是锐角三角形三类
21.(1)2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;;(2)144cm2
【解析】(1)这个六棱柱有8个面,其中2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;
(2)解法一:其侧面积=六棱柱正视图面积×3
六棱柱正视图是三个长方形组成的大长方形,长为12cm,宽为4cm
六棱柱正视图的面积为12×4=48cm2
其侧面积=六棱柱正视图面积×3=48×3=144cm2.
答:这个六棱柱的所有侧面的面积之和为144cm2.
解法二:其侧面积为:6×4×6=144(m2).
答:这个六棱柱的所有侧面的面积之和为144cm2.
22.(1)π,2π,π;(2)两个月牙形的面积之和等于三角形ABC的面积,理由见解析
【解析】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
设四个月牙的面积依次为S1,S2,S3,S4,如图,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径
SAB为直径=S2+S4+S△ABC,
又由(1)可得:∴SAB为直径=SAC为直径+SBC为直径=π,
S1+S2+S3+S4=S2+S4+S△ABC
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
