第4节 简单机械(机械效率及其计算)同步练习(含答案)
文档属性
| 名称 | 第4节 简单机械(机械效率及其计算)同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2021-09-27 19:56:28 | ||
图片预览


文档简介
2021-2022学年浙教版科学机械效率及其计算
一.选择题(共6小题)
1.在下列有关机械效率说法中正确的是( )
A.机械效率较大的,所做功少
B.机械效率较大的,所做的额外功较少
C.机械效率较大的,有用功和额外功的比值较大
D.机械效率较大的,额外功和有用功的比值较大
2.下列说法正确的是( )
A.机械效率不可能大于1
B.做功所用时间越长,功率越小
C.做功越多,功率越大,机械效率越高
D.做的有用功越多的机械,机械效率越高
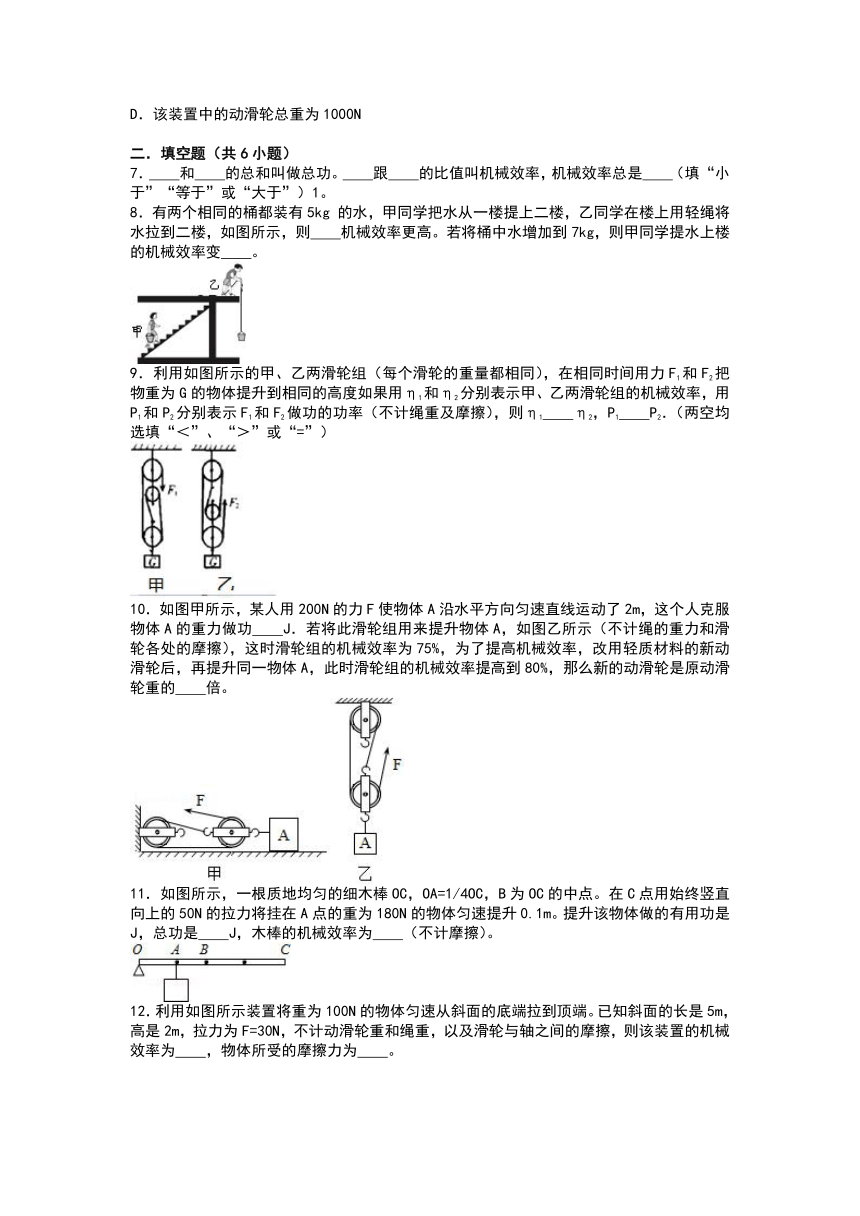
3.如图所示,用两个滑轮分别匀速提升A、B两个物体,拉细绳的力F大小相等,在相同时间内,物体上升的距离也相等,绳重及摩擦不计,滑轮的质量小于物体的质量,甲的有用功为W甲,机械效率为η甲,拉力的功率为P甲;乙的有用功为W乙,机械效率为η乙,拉力的功率为P乙.比较甲、乙两个装置可知( )
A.P甲>P乙
B.P甲<P乙
C.W甲<W乙
η甲<η乙
D.W甲=W乙
η甲<η乙
4.如图所示,小丽分别用甲、乙两滑轮把同一桶沙从一楼地面提到二楼地面,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2,若不计滑轮的摩擦和绳重,则( )
A.W1=W2
η1=η2
B.W1=W2
η1<η2
C.W1<W2
η1>η2
D.W1>W2
η1<η2
5.物理课上刘老师将规格完全相同的滑轮,用相同的绳子绕成甲、乙两个滑轮组,如图所示,分别提起重为G1、G2两个物体,比较它们省力情况和机械效率,不计绳重及摩擦下面四位同学作了四种猜测,你认为正确的是( )
A.甲同学说若G1=G2,则F1<F2,η甲>η乙
B.乙同学说若G1=G2,则F1>F2,η甲<η乙
C.丙同学说若G1<G2,则F1<F2,η甲=η乙
D.丁同学说若G1<G2,则F1<F2,η甲<η乙
6.如图所示滑轮组,在50s内将重5000N货物匀速吊起10m高,绳的自由端受到的拉力大小是1500N,不计绳重及摩擦,关于该滑轮组的说法不正确的是( )
A.滑轮组的机械效率为83.3%
B.绳自由端移动的距离是50m
C.滑轮组所做有用功的功率是1000W
D.该装置中的动滑轮总重为1000N
二.填空题(共6小题)
7. 和 的总和叫做总功。 跟 的比值叫机械效率,机械效率总是 (填“小于”“等于”或“大于”)1。
8.有两个相同的桶都装有5kg
的水,甲同学把水从一楼提上二楼,乙同学在楼上用轻绳将水拉到二楼,如图所示,则 机械效率更高。若将桶中水增加到7kg,则甲同学提水上楼的机械效率变 。
9.利用如图所示的甲、乙两滑轮组(每个滑轮的重量都相同),在相同时间用力F1和F2把物重为G的物体提升到相同的高度如果用η1和η2分别表示甲、乙两滑轮组的机械效率,用P1和P2分别表示F1和F2做功的功率(不计绳重及摩擦),则η1 η2,P1 P2.(两空均选填“<”、“>”或“=”)
10.如图甲所示,某人用200N的力F使物体A沿水平方向匀速直线运动了2m,这个人克服物体A的重力做功 J.若将此滑轮组用来提升物体A,如图乙所示(不计绳的重力和滑轮各处的摩擦),这时滑轮组的机械效率为75%,为了提高机械效率,改用轻质材料的新动滑轮后,再提升同一物体A,此时滑轮组的机械效率提高到80%,那么新的动滑轮是原动滑轮重的 倍。
11.如图所示,一根质地均匀的细木棒OC,OA=1/4OC,B为OC的中点。在C点用始终竖直向上的50N的拉力将挂在A点的重为180N的物体匀速提升0.1m。提升该物体做的有用功是 J,总功是 J,木棒的机械效率为 (不计摩擦)。
12.利用如图所示装置将重为100N的物体匀速从斜面的底端拉到顶端。已知斜面的长是5m,高是2m,拉力为F=30N,不计动滑轮重和绳重,以及滑轮与轴之间的摩擦,则该装置的机械效率为 ,物体所受的摩擦力为 。
三.解答题(共6小题)
13.如图所示,用动滑轮把重400N的物体在20s内匀速提高10m,拉力所做的功为5000J。
求:(1)动滑轮的机械效率
(2)拉力的功率。
14.用如图所示的滑轮组将一质量24kg的物体10s内匀速提高了2m,若所用的拉力为100N,不计绳重和摩擦。(g取10N/kg)
(1)该滑轮组的机械效率为多少?
(2)拉力的功率是多少?
(3)若用此滑轮组匀速提升540N的物体需要多大拉力?
15.如图所示,不计摩擦和绳重,把一个重为40N的物体沿竖直方向在4s内匀速提升了2m,所用的拉力F为25N,则动滑轮重为 N,4s内拉力做功 J,4s内拉力的功率 W,该滑轮组的机械效率为 。
16.在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250N的拉力在20s内将450N的材料提升了10m,(不计绳重和摩擦,g=10N/kg)。求:
(1)拉力的功率是多少?
(2)提升450N材料时,此滑轮组的机械效率是多少?
(3)若绳子能承受的最大拉力为400N时,此滑轮组的机械效率最大可提高到多少?
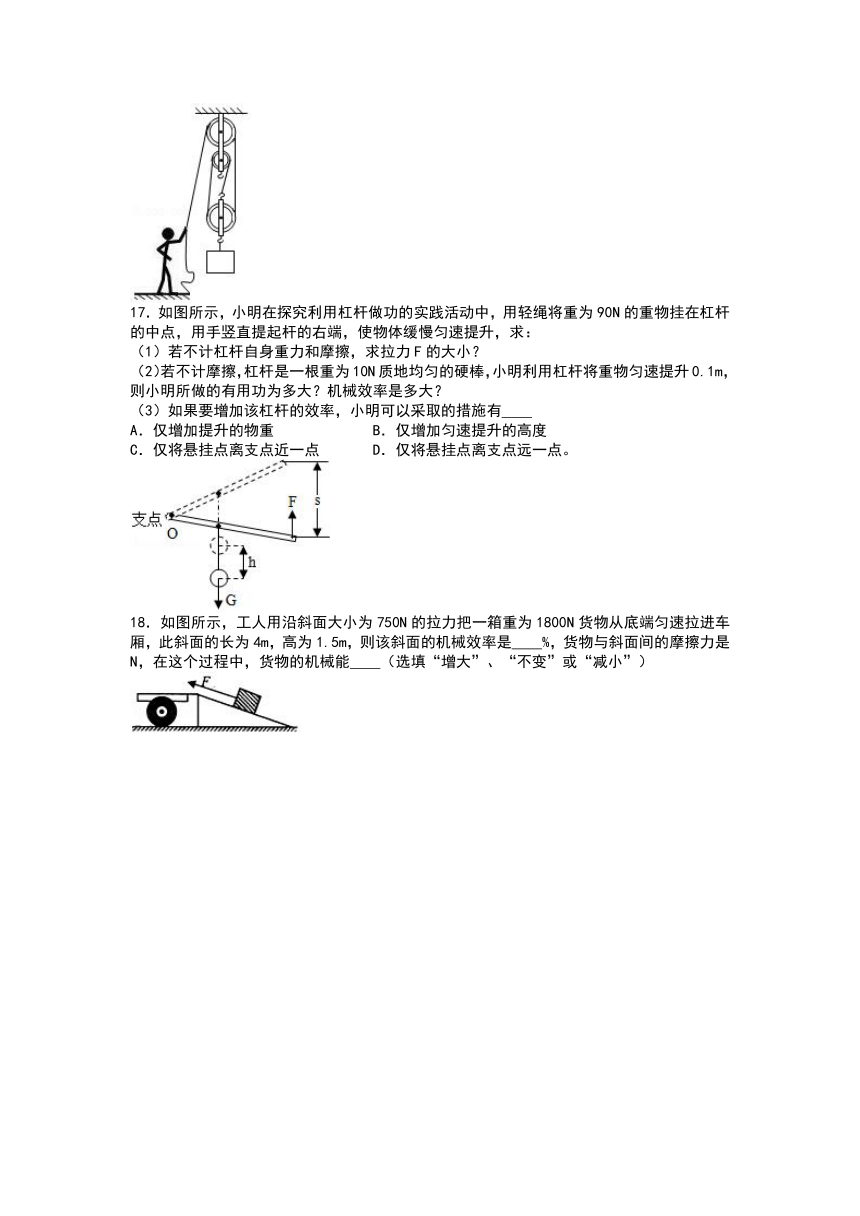
17.如图所示,小明在探究利用杠杆做功的实践活动中,用轻绳将重为90N的重物挂在杠杆的中点,用手竖直提起杆的右端,使物体缓慢匀速提升,求:
(1)若不计杠杆自身重力和摩擦,求拉力F的大小?
(2)若不计摩擦,杠杆是一根重为10N质地均匀的硬棒,小明利用杠杆将重物匀速提升0.1m,则小明所做的有用功为多大?机械效率是多大?
(3)如果要增加该杠杆的效率,小明可以采取的措施有
A.仅增加提升的物重
B.仅增加匀速提升的高度
C.仅将悬挂点离支点近一点
D.仅将悬挂点离支点远一点。
18.如图所示,工人用沿斜面大小为750N的拉力把一箱重为1800N货物从底端匀速拉进车厢,此斜面的长为4m,高为1.5m,则该斜面的机械效率是 %,货物与斜面间的摩擦力是 N,在这个过程中,货物的机械能 (选填“增大”、“不变”或“减小”)
2021-2022学年浙教版科学机械效率及其计算
参考答案与试题解析
一.选择题(共6小题)
1.解:机械效率越大,有用功在总功中所占的比值越大,额外功在总功中所占的比值越小,从而有用功和额外功的比值越大。
故选:C。
2.解:A.使用任何机械都要做额外功,所以总功一定大于有用功,即有用功与总功的比值一定小于1,也就是机械效率小于1,故A正确;
B.由P=可知,做功的多少未知,时间越长,功率不一定越小,故B错误;
C.时间未知,做功越多,功率不一定越大,机械效率与功和功率的多少无关,故C错误;
D.做的有用功越多的机械,总功未知,机械效率不一定越高,故D错误。
故选:A。
3.解:①在不计绳重和摩擦时,用定滑轮提升物体时,定滑轮的机械效率等于1,用动滑轮提升物体时,要克服动滑轮的重,动滑轮的机械效率小于1.所以η甲<η乙。
②在相同时间t内,物体上升的距离h也相等,物体上升的速度v相同,
动滑轮提升物体时,拉力做的总功为:W总=Fs=2Fh,拉力功率为P甲=2Fv。
定滑轮提升物体时,拉力做的总功为:W'总=Fs'=Fh,拉力功率为P乙=Fv。
即P甲=2P乙,所以P甲>P乙.选项A正确、选项B错误;
③根据机械效率公式得,甲的有用功为:W甲=η甲?W总=2Fhη甲,
乙的有用功为:W乙=η乙?W'总=Fhη乙,所以,2W乙=2Fhη乙,
因为不计绳重和摩擦,滑轮的质量小于物体的质量,2η甲>η乙,所以,W甲>W乙.选项C、D错误。
故选:A。
4.解:因为小明分别用甲、乙两滑轮把同一桶沙从一楼地面提到二楼地面,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高。而乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低。即W1<W2
η1>η2。
故选:C。
5.解:AB.由题知,滑轮组都是一定一动,动滑轮重力G轮相同,不计绳重和摩擦,拉力F1=(G+G轮),拉力F2=(G+G轮),如果物重G1=G2,则拉力F1<F2;
机械效率η===,物重相同、动滑轮重相同,机械效率相同,故AB错误;
CD.由题知,滑轮组都是一定一动,动滑轮重力G轮相同,不计绳重和摩擦,拉力F1=(G1+G轮),拉力F2=(G2+G轮),如果物重G1<G2,则拉力F1<F2;
如果物重G1<G2,即物重增大,有用功将增大,不计绳重和摩擦,额外功不变,机械效率η===,所有机械效率将变大,即乙的机械效率高,故C错误、D正确。
故选:D。
6.解:由图可知,n=4,则绳子自由端移动的距离:s=nh=4×10m=40m,故B错误;
有用功:W有=Gh=5000N×10m=5×104J,
滑轮组所做有用功的功率:
P有===1000W,故C正确;
总功:W总=Fs=1500N×40m=6×104J,
滑轮组的机械效率:
η=×100%=×100%=83.3%,故A正确;
不计绳重及摩擦,由F=(G+G动)可得,该装置中的动滑轮总重:
G动=nF﹣G=4×1500N﹣5000N=1000N,故D正确。
故选:B。
二.填空题(共6小题)
7.解:(1)有用功和额外功的总和叫总功,有用功与总功的比值叫机械效率;
(2)使用机械时,不可避免地要做额外功,所以总功一定大于有用功,由η=×100%可知,机械效率一定小于1。
故答案为:有用功;额外功;有用功;总功;小于。
8.解:根据图示可知,甲乙两种方式所做的有用功相同,而甲中的额外功大于乙中的额外功,因此乙的机械效率高;
因为机械效率与物重有关,当其它因素一定时,物重越大,有用功越大,机械效率越大,因此若将桶中水增加到7kg,则甲同学提水上楼的机械效率变大。
故答案为:乙;大。
9.解:(1)由图可知,甲滑轮组中有1个动滑轮,乙滑轮组中有2个动滑轮,
根据题意可知,物重相同都为G,且每个滑轮的重量都相同,
不计绳重及摩擦,滑轮组的机械效率:η====,
所以,甲、乙两滑轮组的机械效率分别为:
η1=,η2=,
比较可知,η1>η2;
(2)用两滑轮组把物重为G的物体都提升到相同的高度,由W有=Gh可知,所做的有用功相同;
因乙滑轮组中2个动滑轮的总重力较大,则克服动滑轮重力做的额外功较多,由W总=W有+W额可知,利用乙滑轮组做的总功较多(即拉力F2做功较多),
已知所用时间相同,根据P=可知,F2做功的功率较大,即P1<P2。
故答案为:>;<。
10.解:(1)物体A沿水平方向匀速直线运动,在重力的方向上没有移动距离,则这个人克服物体A的重力做功为0J;
(2)用如图乙的滑轮组提升物体A时,
不计绳的重力和滑轮各处的摩擦,则滑轮组的机械效率:
η====75%,
则=G+G动,
解得物体A的重力:
G=3G动,﹣﹣﹣﹣﹣①
改用轻质材料的新动滑轮后,再提升同一物体A,此时滑轮组的机械效率:
η′==80%,﹣﹣﹣﹣﹣﹣②
将①代入②可得:
=80%,
化简解得:
G动′=G动=0.75G动。
故答案为:0;0.75。
11.解:提升该物体做的有用功:
W有=Gh=180N×0.1m=18J,
由题意可知,OA=OC,
由相似三角形的性质可知,拉力端(C端)上升的高度:
s=4h=4×0.1m=0.4m,
提升该物体做的总功:
W总=Fs=50N×0.4m=20J;
木棒的机械效率:
η=×100%=×100%=90%。
故答案为:18;20;90%。
12.解:(1)提升重物做的有用功:
W有用=Gh=100N×2m=200J,
在斜面上使用的是动滑轮,拉力端移动的距离:s=2L=2×5m=10m,
拉力所做的总功:
W总=Fs=30N×10m=300J,
该装置的机械效率:
η==×100%≈66.7%;
(2)额外功:W额=W总﹣W有用=300J﹣200J=100J,
不计动滑轮重和绳重,以及滑轮与轴之间的摩擦,克服斜面摩擦力做的功为额外功,
由W额=fL得物体所受的摩擦力:
f===20N。
故答案为:66.7%;20N。
三.解答题(共6小题)
13.解:(1)因为W有用=Gh=400N×10m=4000J,所以η===80%。
(2)P===250W。
答:(1)动滑轮的机械效率是80%;
(2)拉力的功率是250W。
14解:(1)物体受到的重力为G=mg=24kg×10N/kg=240N;
由图知,滑轮组有三段绳子承担物重,则s=3h,
滑轮组的机械效率:
η=×100%=×100%=×100%=×100%=×100%=80%;
(2)W总=Fs=F×3h=100N×3×2m=600J,
拉力的功率:P===60W;
(3)不计绳重和摩擦,拉力F=(G+G轮),
提升240N重物时,100N=×(240N+G轮),
G轮=3×100N﹣240N=60N,
提升540N重物时,拉力F′=(G′+G轮)=×(540N+60N)=200N。
答:(1)该滑轮组的机械效率为80%;
(2)拉力的功率是60W;
(3)若用此滑轮组匀速提升540N的物体需要200N的拉力。
15.解:(1)由图可知,n=2,不计摩擦和绳重,
由F=(G+G动)可得,动滑轮的重力:
G动=nF﹣G=2×25N﹣40N=10N;
(2)绳端移动的距离:
s=nh=2×2m=4m,
4s内拉力做功:
W总=Fs=25N×4m=100J,
拉力的功率:
P===25W,
有用功:
W有=Gh=40N×2m=80J,
滑轮组的机械效率:
η=×100%=×100%=80%。
故答案为:10;100;25;80%。
16.解:(1)由图知,n=3,
则绳子自由端移动的距离:
s=nh=3×10m=30m,
拉力做的功:
W总=Fs=250N×30m=7500J,
则施加拉力的功率:
P===375W;
(2)有用功W有用=Gh=450N×10m=4500J,
机械效率η=×100%=×100%=60%;
(3)由F=(G+G动)可得,
动滑轮的重力G动=nF﹣G=3×250N﹣450N=300N;
由F=(G+G动)可得,
最大物重G′=nF′﹣G动=3×400N﹣300N=900N;
此滑轮组的最大机械效率η′=====75%。
答:(1)拉力的功率是375W;
(2)提升450N材料时,此滑轮组的机械效率是60%;
(3)若绳子能承受的最大拉力为400N时,此滑轮组的机械效率最大可提高到75%。
17.解:(1)由杠杆原理可知:FL1=GL2,即==;
F===45N。
(2)W有用=Gh=90N×0.1m=9J,
W额外=G杆h=10N×0.1m=1J,
W总=W有用+W额外=9J+1J=10J,
η=×100%=×100%=90%。
(3)A.仅增加提升的物重,可以增大有用功,所以可以提高机械效率;
B.仅增加匀速提升的高度,有用功和总功都成相同倍数的变化,所以机械效率不变;
C.仅将悬挂点离支点近一点,物体被提升相同的高度,要把杠杆提升更高的高度,克服杠杆重力做的功更多,即额外功更多,所以机械效率反而降低;
D.仅将悬挂点离支点远一点,物体被提升相同的高度,要把杠杆提升较低的高度,克服杠杆重力做的功减少,即额外功减少,所以机械效率反而升高。
答:(1)不计杠杆自身重力和摩擦,拉力F是4.5N;(2)小明使用杠杆所做的有用功为9J.机械效率是90%;(3)A、D。
18.解:
(1)工人做的有用功W有用=Gh=1800N×1.5m=2700J;
工人做的总功W总=Fs=750N×4m=3000J,
斜面的机械效率η=×100%=×100%=90%;
(2)因为W总=W有用+W额
所以克服摩擦做的额外功W额=W总﹣W有用=3000J﹣2700J=300J,
由W额=fs可得货物与斜面间的摩擦力f===75N;
(3)货物从底端匀速拉进车厢,货物质量不变,所以货物的动能不变,重力势能增大,故货物的机械能增大。
故答案为:90;75;增大。
一.选择题(共6小题)
1.在下列有关机械效率说法中正确的是( )
A.机械效率较大的,所做功少
B.机械效率较大的,所做的额外功较少
C.机械效率较大的,有用功和额外功的比值较大
D.机械效率较大的,额外功和有用功的比值较大
2.下列说法正确的是( )
A.机械效率不可能大于1
B.做功所用时间越长,功率越小
C.做功越多,功率越大,机械效率越高
D.做的有用功越多的机械,机械效率越高
3.如图所示,用两个滑轮分别匀速提升A、B两个物体,拉细绳的力F大小相等,在相同时间内,物体上升的距离也相等,绳重及摩擦不计,滑轮的质量小于物体的质量,甲的有用功为W甲,机械效率为η甲,拉力的功率为P甲;乙的有用功为W乙,机械效率为η乙,拉力的功率为P乙.比较甲、乙两个装置可知( )
A.P甲>P乙
B.P甲<P乙
C.W甲<W乙
η甲<η乙
D.W甲=W乙
η甲<η乙
4.如图所示,小丽分别用甲、乙两滑轮把同一桶沙从一楼地面提到二楼地面,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2,若不计滑轮的摩擦和绳重,则( )
A.W1=W2
η1=η2
B.W1=W2
η1<η2
C.W1<W2
η1>η2
D.W1>W2
η1<η2
5.物理课上刘老师将规格完全相同的滑轮,用相同的绳子绕成甲、乙两个滑轮组,如图所示,分别提起重为G1、G2两个物体,比较它们省力情况和机械效率,不计绳重及摩擦下面四位同学作了四种猜测,你认为正确的是( )
A.甲同学说若G1=G2,则F1<F2,η甲>η乙
B.乙同学说若G1=G2,则F1>F2,η甲<η乙
C.丙同学说若G1<G2,则F1<F2,η甲=η乙
D.丁同学说若G1<G2,则F1<F2,η甲<η乙
6.如图所示滑轮组,在50s内将重5000N货物匀速吊起10m高,绳的自由端受到的拉力大小是1500N,不计绳重及摩擦,关于该滑轮组的说法不正确的是( )
A.滑轮组的机械效率为83.3%
B.绳自由端移动的距离是50m
C.滑轮组所做有用功的功率是1000W
D.该装置中的动滑轮总重为1000N
二.填空题(共6小题)
7. 和 的总和叫做总功。 跟 的比值叫机械效率,机械效率总是 (填“小于”“等于”或“大于”)1。
8.有两个相同的桶都装有5kg
的水,甲同学把水从一楼提上二楼,乙同学在楼上用轻绳将水拉到二楼,如图所示,则 机械效率更高。若将桶中水增加到7kg,则甲同学提水上楼的机械效率变 。
9.利用如图所示的甲、乙两滑轮组(每个滑轮的重量都相同),在相同时间用力F1和F2把物重为G的物体提升到相同的高度如果用η1和η2分别表示甲、乙两滑轮组的机械效率,用P1和P2分别表示F1和F2做功的功率(不计绳重及摩擦),则η1 η2,P1 P2.(两空均选填“<”、“>”或“=”)
10.如图甲所示,某人用200N的力F使物体A沿水平方向匀速直线运动了2m,这个人克服物体A的重力做功 J.若将此滑轮组用来提升物体A,如图乙所示(不计绳的重力和滑轮各处的摩擦),这时滑轮组的机械效率为75%,为了提高机械效率,改用轻质材料的新动滑轮后,再提升同一物体A,此时滑轮组的机械效率提高到80%,那么新的动滑轮是原动滑轮重的 倍。
11.如图所示,一根质地均匀的细木棒OC,OA=1/4OC,B为OC的中点。在C点用始终竖直向上的50N的拉力将挂在A点的重为180N的物体匀速提升0.1m。提升该物体做的有用功是 J,总功是 J,木棒的机械效率为 (不计摩擦)。
12.利用如图所示装置将重为100N的物体匀速从斜面的底端拉到顶端。已知斜面的长是5m,高是2m,拉力为F=30N,不计动滑轮重和绳重,以及滑轮与轴之间的摩擦,则该装置的机械效率为 ,物体所受的摩擦力为 。
三.解答题(共6小题)
13.如图所示,用动滑轮把重400N的物体在20s内匀速提高10m,拉力所做的功为5000J。
求:(1)动滑轮的机械效率
(2)拉力的功率。
14.用如图所示的滑轮组将一质量24kg的物体10s内匀速提高了2m,若所用的拉力为100N,不计绳重和摩擦。(g取10N/kg)
(1)该滑轮组的机械效率为多少?
(2)拉力的功率是多少?
(3)若用此滑轮组匀速提升540N的物体需要多大拉力?
15.如图所示,不计摩擦和绳重,把一个重为40N的物体沿竖直方向在4s内匀速提升了2m,所用的拉力F为25N,则动滑轮重为 N,4s内拉力做功 J,4s内拉力的功率 W,该滑轮组的机械效率为 。
16.在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250N的拉力在20s内将450N的材料提升了10m,(不计绳重和摩擦,g=10N/kg)。求:
(1)拉力的功率是多少?
(2)提升450N材料时,此滑轮组的机械效率是多少?
(3)若绳子能承受的最大拉力为400N时,此滑轮组的机械效率最大可提高到多少?
17.如图所示,小明在探究利用杠杆做功的实践活动中,用轻绳将重为90N的重物挂在杠杆的中点,用手竖直提起杆的右端,使物体缓慢匀速提升,求:
(1)若不计杠杆自身重力和摩擦,求拉力F的大小?
(2)若不计摩擦,杠杆是一根重为10N质地均匀的硬棒,小明利用杠杆将重物匀速提升0.1m,则小明所做的有用功为多大?机械效率是多大?
(3)如果要增加该杠杆的效率,小明可以采取的措施有
A.仅增加提升的物重
B.仅增加匀速提升的高度
C.仅将悬挂点离支点近一点
D.仅将悬挂点离支点远一点。
18.如图所示,工人用沿斜面大小为750N的拉力把一箱重为1800N货物从底端匀速拉进车厢,此斜面的长为4m,高为1.5m,则该斜面的机械效率是 %,货物与斜面间的摩擦力是 N,在这个过程中,货物的机械能 (选填“增大”、“不变”或“减小”)
2021-2022学年浙教版科学机械效率及其计算
参考答案与试题解析
一.选择题(共6小题)
1.解:机械效率越大,有用功在总功中所占的比值越大,额外功在总功中所占的比值越小,从而有用功和额外功的比值越大。
故选:C。
2.解:A.使用任何机械都要做额外功,所以总功一定大于有用功,即有用功与总功的比值一定小于1,也就是机械效率小于1,故A正确;
B.由P=可知,做功的多少未知,时间越长,功率不一定越小,故B错误;
C.时间未知,做功越多,功率不一定越大,机械效率与功和功率的多少无关,故C错误;
D.做的有用功越多的机械,总功未知,机械效率不一定越高,故D错误。
故选:A。
3.解:①在不计绳重和摩擦时,用定滑轮提升物体时,定滑轮的机械效率等于1,用动滑轮提升物体时,要克服动滑轮的重,动滑轮的机械效率小于1.所以η甲<η乙。
②在相同时间t内,物体上升的距离h也相等,物体上升的速度v相同,
动滑轮提升物体时,拉力做的总功为:W总=Fs=2Fh,拉力功率为P甲=2Fv。
定滑轮提升物体时,拉力做的总功为:W'总=Fs'=Fh,拉力功率为P乙=Fv。
即P甲=2P乙,所以P甲>P乙.选项A正确、选项B错误;
③根据机械效率公式得,甲的有用功为:W甲=η甲?W总=2Fhη甲,
乙的有用功为:W乙=η乙?W'总=Fhη乙,所以,2W乙=2Fhη乙,
因为不计绳重和摩擦,滑轮的质量小于物体的质量,2η甲>η乙,所以,W甲>W乙.选项C、D错误。
故选:A。
4.解:因为小明分别用甲、乙两滑轮把同一桶沙从一楼地面提到二楼地面,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高。而乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低。即W1<W2
η1>η2。
故选:C。
5.解:AB.由题知,滑轮组都是一定一动,动滑轮重力G轮相同,不计绳重和摩擦,拉力F1=(G+G轮),拉力F2=(G+G轮),如果物重G1=G2,则拉力F1<F2;
机械效率η===,物重相同、动滑轮重相同,机械效率相同,故AB错误;
CD.由题知,滑轮组都是一定一动,动滑轮重力G轮相同,不计绳重和摩擦,拉力F1=(G1+G轮),拉力F2=(G2+G轮),如果物重G1<G2,则拉力F1<F2;
如果物重G1<G2,即物重增大,有用功将增大,不计绳重和摩擦,额外功不变,机械效率η===,所有机械效率将变大,即乙的机械效率高,故C错误、D正确。
故选:D。
6.解:由图可知,n=4,则绳子自由端移动的距离:s=nh=4×10m=40m,故B错误;
有用功:W有=Gh=5000N×10m=5×104J,
滑轮组所做有用功的功率:
P有===1000W,故C正确;
总功:W总=Fs=1500N×40m=6×104J,
滑轮组的机械效率:
η=×100%=×100%=83.3%,故A正确;
不计绳重及摩擦,由F=(G+G动)可得,该装置中的动滑轮总重:
G动=nF﹣G=4×1500N﹣5000N=1000N,故D正确。
故选:B。
二.填空题(共6小题)
7.解:(1)有用功和额外功的总和叫总功,有用功与总功的比值叫机械效率;
(2)使用机械时,不可避免地要做额外功,所以总功一定大于有用功,由η=×100%可知,机械效率一定小于1。
故答案为:有用功;额外功;有用功;总功;小于。
8.解:根据图示可知,甲乙两种方式所做的有用功相同,而甲中的额外功大于乙中的额外功,因此乙的机械效率高;
因为机械效率与物重有关,当其它因素一定时,物重越大,有用功越大,机械效率越大,因此若将桶中水增加到7kg,则甲同学提水上楼的机械效率变大。
故答案为:乙;大。
9.解:(1)由图可知,甲滑轮组中有1个动滑轮,乙滑轮组中有2个动滑轮,
根据题意可知,物重相同都为G,且每个滑轮的重量都相同,
不计绳重及摩擦,滑轮组的机械效率:η====,
所以,甲、乙两滑轮组的机械效率分别为:
η1=,η2=,
比较可知,η1>η2;
(2)用两滑轮组把物重为G的物体都提升到相同的高度,由W有=Gh可知,所做的有用功相同;
因乙滑轮组中2个动滑轮的总重力较大,则克服动滑轮重力做的额外功较多,由W总=W有+W额可知,利用乙滑轮组做的总功较多(即拉力F2做功较多),
已知所用时间相同,根据P=可知,F2做功的功率较大,即P1<P2。
故答案为:>;<。
10.解:(1)物体A沿水平方向匀速直线运动,在重力的方向上没有移动距离,则这个人克服物体A的重力做功为0J;
(2)用如图乙的滑轮组提升物体A时,
不计绳的重力和滑轮各处的摩擦,则滑轮组的机械效率:
η====75%,
则=G+G动,
解得物体A的重力:
G=3G动,﹣﹣﹣﹣﹣①
改用轻质材料的新动滑轮后,再提升同一物体A,此时滑轮组的机械效率:
η′==80%,﹣﹣﹣﹣﹣﹣②
将①代入②可得:
=80%,
化简解得:
G动′=G动=0.75G动。
故答案为:0;0.75。
11.解:提升该物体做的有用功:
W有=Gh=180N×0.1m=18J,
由题意可知,OA=OC,
由相似三角形的性质可知,拉力端(C端)上升的高度:
s=4h=4×0.1m=0.4m,
提升该物体做的总功:
W总=Fs=50N×0.4m=20J;
木棒的机械效率:
η=×100%=×100%=90%。
故答案为:18;20;90%。
12.解:(1)提升重物做的有用功:
W有用=Gh=100N×2m=200J,
在斜面上使用的是动滑轮,拉力端移动的距离:s=2L=2×5m=10m,
拉力所做的总功:
W总=Fs=30N×10m=300J,
该装置的机械效率:
η==×100%≈66.7%;
(2)额外功:W额=W总﹣W有用=300J﹣200J=100J,
不计动滑轮重和绳重,以及滑轮与轴之间的摩擦,克服斜面摩擦力做的功为额外功,
由W额=fL得物体所受的摩擦力:
f===20N。
故答案为:66.7%;20N。
三.解答题(共6小题)
13.解:(1)因为W有用=Gh=400N×10m=4000J,所以η===80%。
(2)P===250W。
答:(1)动滑轮的机械效率是80%;
(2)拉力的功率是250W。
14解:(1)物体受到的重力为G=mg=24kg×10N/kg=240N;
由图知,滑轮组有三段绳子承担物重,则s=3h,
滑轮组的机械效率:
η=×100%=×100%=×100%=×100%=×100%=80%;
(2)W总=Fs=F×3h=100N×3×2m=600J,
拉力的功率:P===60W;
(3)不计绳重和摩擦,拉力F=(G+G轮),
提升240N重物时,100N=×(240N+G轮),
G轮=3×100N﹣240N=60N,
提升540N重物时,拉力F′=(G′+G轮)=×(540N+60N)=200N。
答:(1)该滑轮组的机械效率为80%;
(2)拉力的功率是60W;
(3)若用此滑轮组匀速提升540N的物体需要200N的拉力。
15.解:(1)由图可知,n=2,不计摩擦和绳重,
由F=(G+G动)可得,动滑轮的重力:
G动=nF﹣G=2×25N﹣40N=10N;
(2)绳端移动的距离:
s=nh=2×2m=4m,
4s内拉力做功:
W总=Fs=25N×4m=100J,
拉力的功率:
P===25W,
有用功:
W有=Gh=40N×2m=80J,
滑轮组的机械效率:
η=×100%=×100%=80%。
故答案为:10;100;25;80%。
16.解:(1)由图知,n=3,
则绳子自由端移动的距离:
s=nh=3×10m=30m,
拉力做的功:
W总=Fs=250N×30m=7500J,
则施加拉力的功率:
P===375W;
(2)有用功W有用=Gh=450N×10m=4500J,
机械效率η=×100%=×100%=60%;
(3)由F=(G+G动)可得,
动滑轮的重力G动=nF﹣G=3×250N﹣450N=300N;
由F=(G+G动)可得,
最大物重G′=nF′﹣G动=3×400N﹣300N=900N;
此滑轮组的最大机械效率η′=====75%。
答:(1)拉力的功率是375W;
(2)提升450N材料时,此滑轮组的机械效率是60%;
(3)若绳子能承受的最大拉力为400N时,此滑轮组的机械效率最大可提高到75%。
17.解:(1)由杠杆原理可知:FL1=GL2,即==;
F===45N。
(2)W有用=Gh=90N×0.1m=9J,
W额外=G杆h=10N×0.1m=1J,
W总=W有用+W额外=9J+1J=10J,
η=×100%=×100%=90%。
(3)A.仅增加提升的物重,可以增大有用功,所以可以提高机械效率;
B.仅增加匀速提升的高度,有用功和总功都成相同倍数的变化,所以机械效率不变;
C.仅将悬挂点离支点近一点,物体被提升相同的高度,要把杠杆提升更高的高度,克服杠杆重力做的功更多,即额外功更多,所以机械效率反而降低;
D.仅将悬挂点离支点远一点,物体被提升相同的高度,要把杠杆提升较低的高度,克服杠杆重力做的功减少,即额外功减少,所以机械效率反而升高。
答:(1)不计杠杆自身重力和摩擦,拉力F是4.5N;(2)小明使用杠杆所做的有用功为9J.机械效率是90%;(3)A、D。
18.解:
(1)工人做的有用功W有用=Gh=1800N×1.5m=2700J;
工人做的总功W总=Fs=750N×4m=3000J,
斜面的机械效率η=×100%=×100%=90%;
(2)因为W总=W有用+W额
所以克服摩擦做的额外功W额=W总﹣W有用=3000J﹣2700J=300J,
由W额=fs可得货物与斜面间的摩擦力f===75N;
(3)货物从底端匀速拉进车厢,货物质量不变,所以货物的动能不变,重力势能增大,故货物的机械能增大。
故答案为:90;75;增大。
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
