2021-2022学年九年级数学苏科版上册2.4圆周角 常考辅导训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年九年级数学苏科版上册2.4圆周角 常考辅导训练(word版、含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 384.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 00:00:00 | ||
图片预览
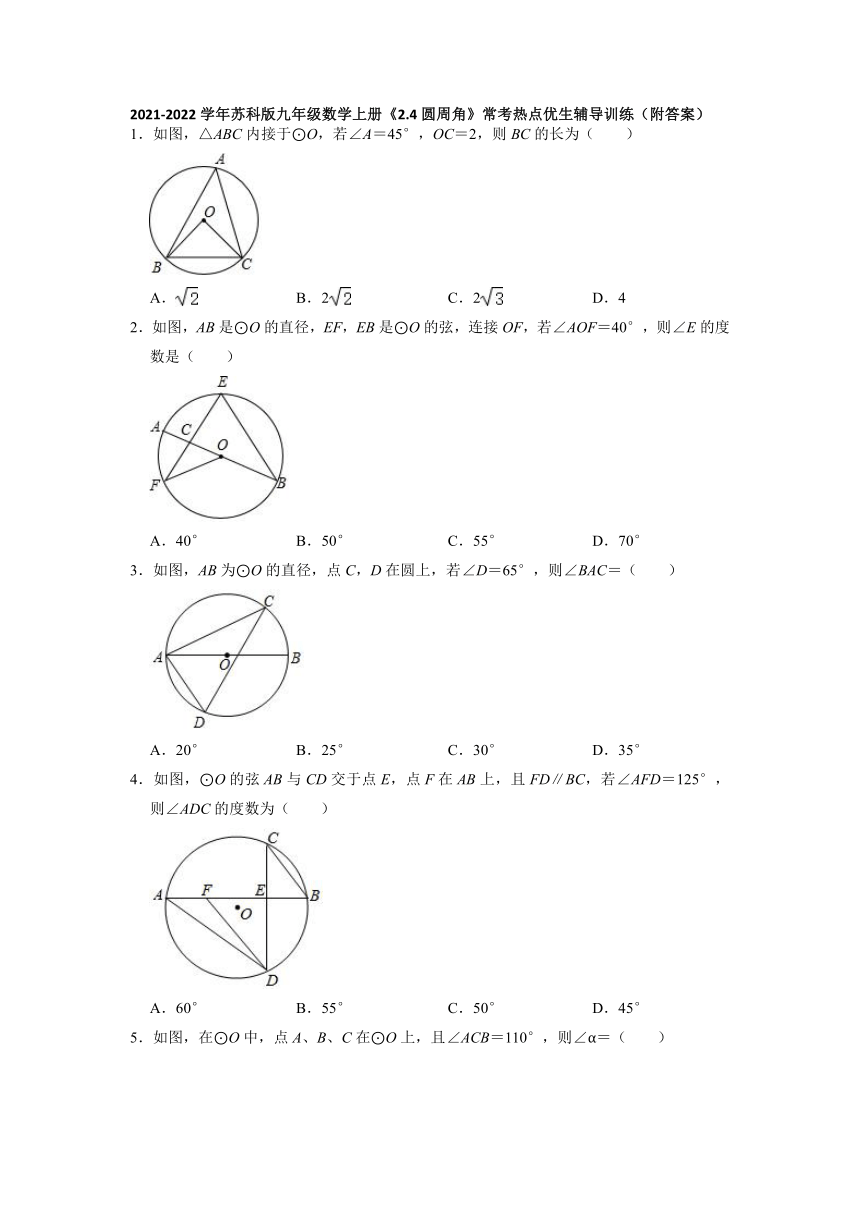



文档简介
2021-2022学年苏科版九年级数学上册《2.4圆周角》常考热点优生辅导训练(附答案)
1.如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A.
B.2
C.2
D.4
2.如图,AB是⊙O的直径,EF,EB是⊙O的弦,连接OF,若∠AOF=40°,则∠E的度数是( )
A.40°
B.50°
C.55°
D.70°
3.如图,AB为⊙O的直径,点C,D在圆上,若∠D=65°,则∠BAC=( )
A.20°
B.25°
C.30°
D.35°
4.如图,⊙O的弦AB与CD交于点E,点F在AB上,且FD∥BC,若∠AFD=125°,则∠ADC的度数为( )
A.60°
B.55°
C.50°
D.45°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70°
B.110°
C.120°
D.140°
6.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45°
B.60°
C.45°
或135°
D.60°
或120°
7.如图,已知四边形ABCD为⊙O的内接四边形,BD平分∠ABC,DH⊥AB于点H,DH=,∠ABC=120°,则AB+BC的值为( )
A.
B.
C.2
D.
8.如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2
B.4
C.
D.2
9.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果=,则∠ACD的度数是
.
10.如图,四边形ABCD内接于⊙O,延长CO交⊙O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD=
°.
11.在⊙O中,半径OA=1,AB、AC为弦,AB=,AC=,则∠BAC=
.
12.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为
度.
13.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F,∠A=50°,则∠E+∠F=
.
14.如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为
.
15.已知△ABC内接于⊙O,若∠BOC=100°,则∠BAC=
°.
16.如图,AB是⊙O的一条弦,P是⊙O上一动点(不与点A,B重合),C,D分别是AB,BP的中点.若AB=4,∠APB=45°,则CD长的最大值为
.
17.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求DB的长.
18.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8,CD=24,求⊙O的直径.
19.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.
21.如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)过点B作BE∥CD交DA的延长线于点E,若AD=2,DC=3,求△BDE的面积.
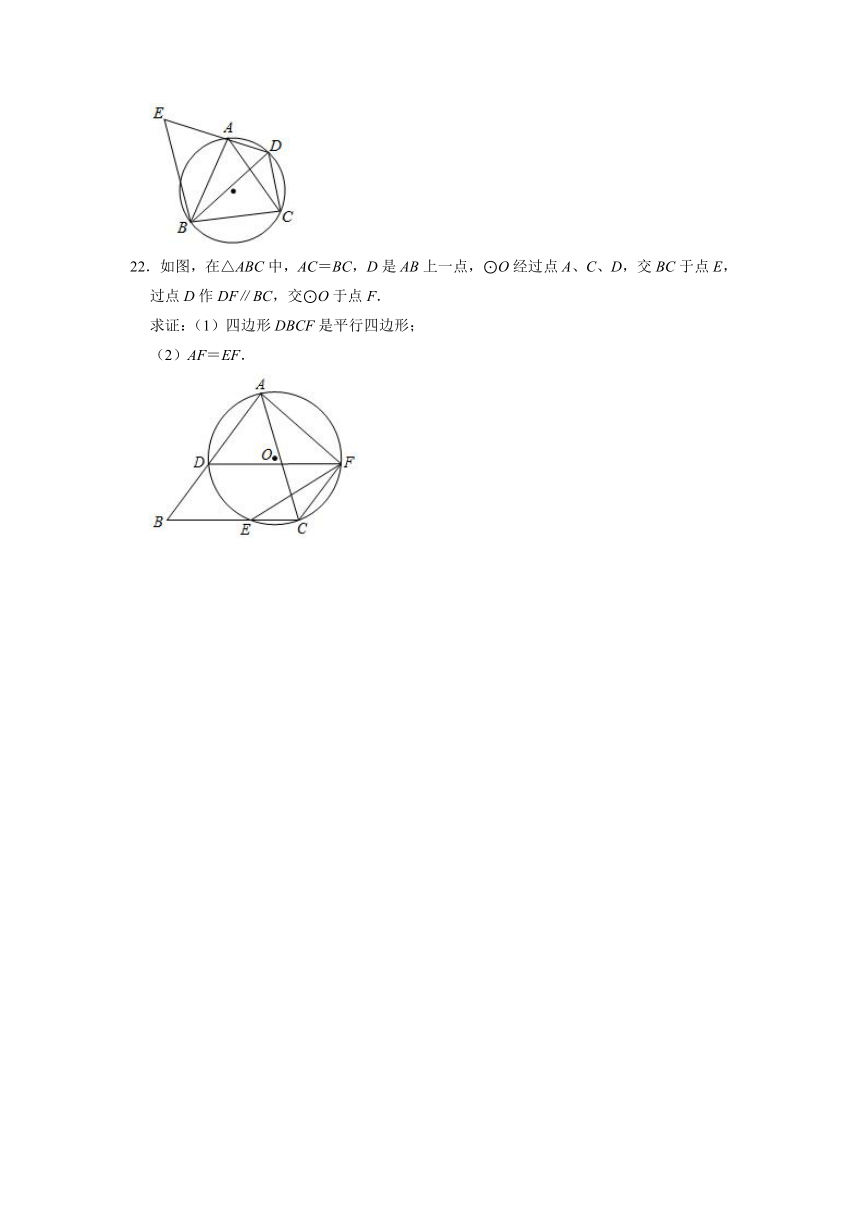
22.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案
1.解:由圆周角定理得,∠BOC=2∠A=90°,
∴BC=OC=2,
故选:B.
2.解:∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠E=∠FOB=70°
故选:D.
3.解:连接BC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠B=∠D=65°,
∴∠BAC=90°﹣∠B=90°﹣65°=25°.
故选:B.
4.解:∵∠EFD+∠AFD=180°,
∴∠EFD=180°﹣125°=55°,
∵FD∥BC,
∴∠B=∠EFD=55°,
∴∠ADC=∠B=55°.
故选:B.
5.解:作所对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣110°=70°,
∴∠AOB=2∠ADB=140°.
故选:D.
6.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
7.解:延长BA到E,使AE=BC,连接DE,如图,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=×120°=60°,
∵∠DAC=∠DBC=60°,∠DCA=∠DBA=60°,
∴△DAC为等边三角形,
∴DA=DC,
在△ADE和△BCD中,
,
∴△ADE≌△BCD(SAS),
∴∠E=∠DBC=60°,
而∠DBA=60°,
∴△DBE为等边三角形,
∵DH⊥AB,
∴BH=EH,
在Rt△BDH中,BH=DH=×=1,
∴BE=2BH=2,
∴AB+BC=2.
故选:C.
8.解:连接OC,如图,
∵∠ADC=30°,
∴∠AOC=60°,
∵OA⊥BC,
∴CE=BE,
在Rt△COE中,OE=OC,CE=OE,
∵OE=OA﹣AE=OC﹣1,
∴OC﹣1=OC,
∴OC=2,
∴OE=1,
∴CE=,
∴BC=2CE=2.
故选:D.
9.解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵=,
∴==,
即、、的度数是=120°,
∴∠ACD=°=60°,
故答案为:60°.
10.解:∵EC是⊙O的直径,
∴∠EBC=90°,
∴∠BCE=90°﹣∠E=30°,
∵四边形ABCD内接于⊙O,
∴∠BCD=180°﹣∠A=80°,
∴∠ECD=∠BCD﹣∠BCE=50°,
故答案为:50
11.解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,根据垂径定理得AE=AC=,AD=AB=,
∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°﹣60°=30°,
∴∠BAC=45°+30°=75°,
或∠BAC′=45°﹣30°=15°.
故答案为:15°或75°.
12.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°,
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°,
故答案为:50.
13.解:∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,∠ECD=∠A=50°,∠BCF=∠A=50°,
∴∠EDC+∠FBC=180°,
∴∠E+∠F=360°﹣180°﹣50°﹣50°=80°,
故答案为:80°.
14.解:连接OC,OD,
∵量角器上的C、D两点所表示的读数分别是80°、50°,
∴∠AOC=50°,∠AOD=80°,
∴∠COD=∠AOD﹣∠AOC=30°,
∴∠DBC=∠COD=15°.
故答案为:15°.
15.解:∵如图,若A在优弧BC上时,∠BAC=∠BOC=×100°=50°;
若点A在劣弧BC上时,∠BA′C=180°﹣∠BAC=130°.
∴∠BAC=50°或130°.
故答案为:50或130.
16.解:∵C,D分别是AB,BP的中点
∴CD=AP,
当AP为直径时,CD长最大,
∵AP为直径,
∴∠ABP=90°,且∠APB=45°,AB=4,
∴AP=4
∴CD长的最大值为2
故答案为2
17.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠B=∠ACD=30°,
∴∠BAD=90°﹣∠B=90°﹣30°=60°;
(2)在Rt△ADB中,BD=AD=×=3.
18.(1)证明:∵AB⊥CD,
∴,
∴∠A=∠BCD,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)解:设⊙O的半径为r,则OC=r,OE=OA﹣BE=r﹣8,
∵AB⊥CD,
∴CE=DE=CD=×24=12,
在Rt△OCE中,122+(r﹣8)2=r2,解得r=13,
∴⊙O的直径=2r=26.
19.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
20.解:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠CEB=90°,
∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,
∴∠1=∠2,
∴CF=BF;
(2)∵C是弧BD的中点,
∴=,
∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,
∴⊙O的半径为10,
∵S△ABC=AC?BC=AB?CE,
∴CE==9.6.
21.(1)证明:∵四边形ABCD内接于圆.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形.
(2)过点A作AM⊥CD,垂足为点M,过点B作BN⊥AC,垂足为点N.
∴∠AMD=90°,
∵∠ADC=120°,
∴∠ADM=60°,
∴∠DAM=30°,
∴DM=AD=1,AM===,
∵CD=3,
∴CM=CD+DM=1+3=4,
∴S△ACD=CD?AM=×=,
Rt△AMC中,∠AMD=90°,
∴AC===,
∵△ABC是等边三角形,
∴AB=BC=AC=,
∴BN=BC=,
∴S△ABC=×=,
∴四边形ABCD的面积=+=,
∵BE∥CD,
∴∠E+∠ADC=180°,
∵∠ADC=120°,
∴∠E=60°,
∴∠E=∠BDC,
∵四边形ABCD内接于⊙O,
∴∠EAB=∠BCD,
在△EAB和△DCB中,
,
∴△EAB≌△DCB(AAS),
∴△BDE的面积=四边形ABCD的面积=.
方法二
(2)∵BE∥CD,
∴∠EBD=∠BDC,
∵∠ADB=∠CDB=60°,
∴∠EBD=∠EDB=60°,
∴△BDE是等边三角形,
又∵△ABC为等边三角形,
∴∠EBD=∠ABC=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD=3,
∴DE=AE+AD=5,
∴△BDE的面积==
22.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
1.如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A.
B.2
C.2
D.4
2.如图,AB是⊙O的直径,EF,EB是⊙O的弦,连接OF,若∠AOF=40°,则∠E的度数是( )
A.40°
B.50°
C.55°
D.70°
3.如图,AB为⊙O的直径,点C,D在圆上,若∠D=65°,则∠BAC=( )
A.20°
B.25°
C.30°
D.35°
4.如图,⊙O的弦AB与CD交于点E,点F在AB上,且FD∥BC,若∠AFD=125°,则∠ADC的度数为( )
A.60°
B.55°
C.50°
D.45°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70°
B.110°
C.120°
D.140°
6.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45°
B.60°
C.45°
或135°
D.60°
或120°
7.如图,已知四边形ABCD为⊙O的内接四边形,BD平分∠ABC,DH⊥AB于点H,DH=,∠ABC=120°,则AB+BC的值为( )
A.
B.
C.2
D.
8.如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2
B.4
C.
D.2
9.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果=,则∠ACD的度数是
.
10.如图,四边形ABCD内接于⊙O,延长CO交⊙O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD=
°.
11.在⊙O中,半径OA=1,AB、AC为弦,AB=,AC=,则∠BAC=
.
12.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为
度.
13.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F,∠A=50°,则∠E+∠F=
.
14.如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为
.
15.已知△ABC内接于⊙O,若∠BOC=100°,则∠BAC=
°.
16.如图,AB是⊙O的一条弦,P是⊙O上一动点(不与点A,B重合),C,D分别是AB,BP的中点.若AB=4,∠APB=45°,则CD长的最大值为
.
17.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求DB的长.
18.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8,CD=24,求⊙O的直径.
19.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.
21.如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)过点B作BE∥CD交DA的延长线于点E,若AD=2,DC=3,求△BDE的面积.
22.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案
1.解:由圆周角定理得,∠BOC=2∠A=90°,
∴BC=OC=2,
故选:B.
2.解:∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠E=∠FOB=70°
故选:D.
3.解:连接BC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠B=∠D=65°,
∴∠BAC=90°﹣∠B=90°﹣65°=25°.
故选:B.
4.解:∵∠EFD+∠AFD=180°,
∴∠EFD=180°﹣125°=55°,
∵FD∥BC,
∴∠B=∠EFD=55°,
∴∠ADC=∠B=55°.
故选:B.
5.解:作所对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣110°=70°,
∴∠AOB=2∠ADB=140°.
故选:D.
6.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
7.解:延长BA到E,使AE=BC,连接DE,如图,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=×120°=60°,
∵∠DAC=∠DBC=60°,∠DCA=∠DBA=60°,
∴△DAC为等边三角形,
∴DA=DC,
在△ADE和△BCD中,
,
∴△ADE≌△BCD(SAS),
∴∠E=∠DBC=60°,
而∠DBA=60°,
∴△DBE为等边三角形,
∵DH⊥AB,
∴BH=EH,
在Rt△BDH中,BH=DH=×=1,
∴BE=2BH=2,
∴AB+BC=2.
故选:C.
8.解:连接OC,如图,
∵∠ADC=30°,
∴∠AOC=60°,
∵OA⊥BC,
∴CE=BE,
在Rt△COE中,OE=OC,CE=OE,
∵OE=OA﹣AE=OC﹣1,
∴OC﹣1=OC,
∴OC=2,
∴OE=1,
∴CE=,
∴BC=2CE=2.
故选:D.
9.解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵=,
∴==,
即、、的度数是=120°,
∴∠ACD=°=60°,
故答案为:60°.
10.解:∵EC是⊙O的直径,
∴∠EBC=90°,
∴∠BCE=90°﹣∠E=30°,
∵四边形ABCD内接于⊙O,
∴∠BCD=180°﹣∠A=80°,
∴∠ECD=∠BCD﹣∠BCE=50°,
故答案为:50
11.解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,根据垂径定理得AE=AC=,AD=AB=,
∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°﹣60°=30°,
∴∠BAC=45°+30°=75°,
或∠BAC′=45°﹣30°=15°.
故答案为:15°或75°.
12.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°,
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°,
故答案为:50.
13.解:∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,∠ECD=∠A=50°,∠BCF=∠A=50°,
∴∠EDC+∠FBC=180°,
∴∠E+∠F=360°﹣180°﹣50°﹣50°=80°,
故答案为:80°.
14.解:连接OC,OD,
∵量角器上的C、D两点所表示的读数分别是80°、50°,
∴∠AOC=50°,∠AOD=80°,
∴∠COD=∠AOD﹣∠AOC=30°,
∴∠DBC=∠COD=15°.
故答案为:15°.
15.解:∵如图,若A在优弧BC上时,∠BAC=∠BOC=×100°=50°;
若点A在劣弧BC上时,∠BA′C=180°﹣∠BAC=130°.
∴∠BAC=50°或130°.
故答案为:50或130.
16.解:∵C,D分别是AB,BP的中点
∴CD=AP,
当AP为直径时,CD长最大,
∵AP为直径,
∴∠ABP=90°,且∠APB=45°,AB=4,
∴AP=4
∴CD长的最大值为2
故答案为2
17.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠B=∠ACD=30°,
∴∠BAD=90°﹣∠B=90°﹣30°=60°;
(2)在Rt△ADB中,BD=AD=×=3.
18.(1)证明:∵AB⊥CD,
∴,
∴∠A=∠BCD,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)解:设⊙O的半径为r,则OC=r,OE=OA﹣BE=r﹣8,
∵AB⊥CD,
∴CE=DE=CD=×24=12,
在Rt△OCE中,122+(r﹣8)2=r2,解得r=13,
∴⊙O的直径=2r=26.
19.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
20.解:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠CEB=90°,
∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,
∴∠1=∠2,
∴CF=BF;
(2)∵C是弧BD的中点,
∴=,
∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,
∴⊙O的半径为10,
∵S△ABC=AC?BC=AB?CE,
∴CE==9.6.
21.(1)证明:∵四边形ABCD内接于圆.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形.
(2)过点A作AM⊥CD,垂足为点M,过点B作BN⊥AC,垂足为点N.
∴∠AMD=90°,
∵∠ADC=120°,
∴∠ADM=60°,
∴∠DAM=30°,
∴DM=AD=1,AM===,
∵CD=3,
∴CM=CD+DM=1+3=4,
∴S△ACD=CD?AM=×=,
Rt△AMC中,∠AMD=90°,
∴AC===,
∵△ABC是等边三角形,
∴AB=BC=AC=,
∴BN=BC=,
∴S△ABC=×=,
∴四边形ABCD的面积=+=,
∵BE∥CD,
∴∠E+∠ADC=180°,
∵∠ADC=120°,
∴∠E=60°,
∴∠E=∠BDC,
∵四边形ABCD内接于⊙O,
∴∠EAB=∠BCD,
在△EAB和△DCB中,
,
∴△EAB≌△DCB(AAS),
∴△BDE的面积=四边形ABCD的面积=.
方法二
(2)∵BE∥CD,
∴∠EBD=∠BDC,
∵∠ADB=∠CDB=60°,
∴∠EBD=∠EDB=60°,
∴△BDE是等边三角形,
又∵△ABC为等边三角形,
∴∠EBD=∠ABC=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD=3,
∴DE=AE+AD=5,
∴△BDE的面积==
22.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
