人教版八年级上册数学 12.3 角平分线的性质第2课时 角平分线的判定(共23张)
文档属性
| 名称 | 人教版八年级上册数学 12.3 角平分线的性质第2课时 角平分线的判定(共23张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 19:16:48 | ||
图片预览






文档简介
(共23张PPT)
12.3
角平分线的性质
第2课时
角平分线的判定
教学目标
1.理解角平分线判定定理.(难点)
2.掌握角平分线判定定理内容的证明方法并应用其解题.(重点)
3.学会判断一个点是否在一个角的平分线上.
复习导入
1、写出命题“全等三角形的对应边相等”的逆命题.
1、写出命题“角平分线上的点到角的两边的距离相等”
的逆命题.
我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
几何语言:
猜想:
角平分线的判定
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
例1.
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
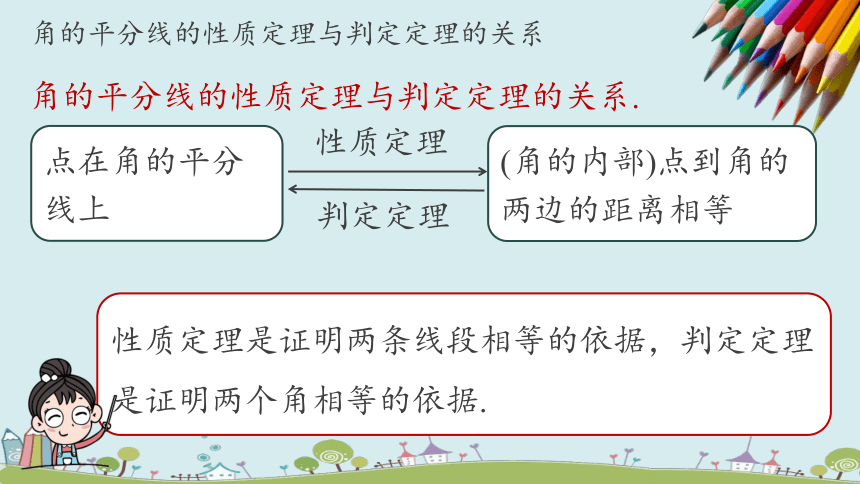
角的平分线的性质定理与判定定理的关系.
点在角的平分线上
(角的内部)点到角的两边的距离相等
性质定理
判定定理
性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
角的平分线的性质定理与判定定理的关系
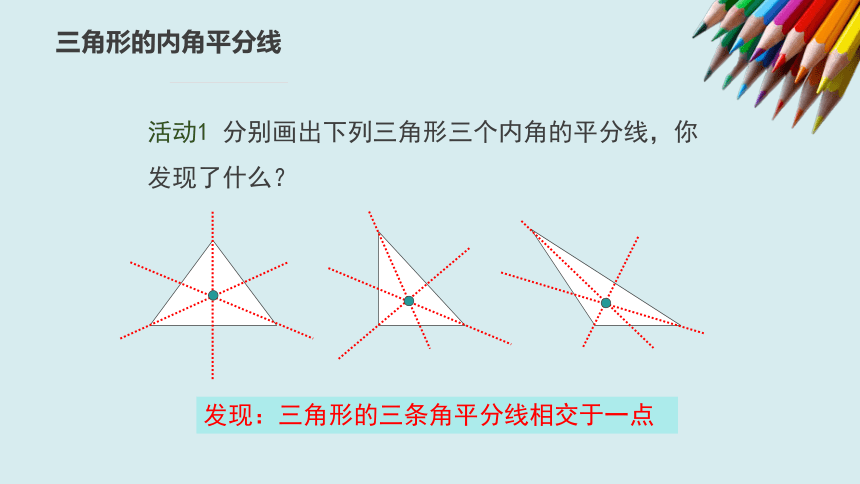
活动1
分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
三角形的内角平分线
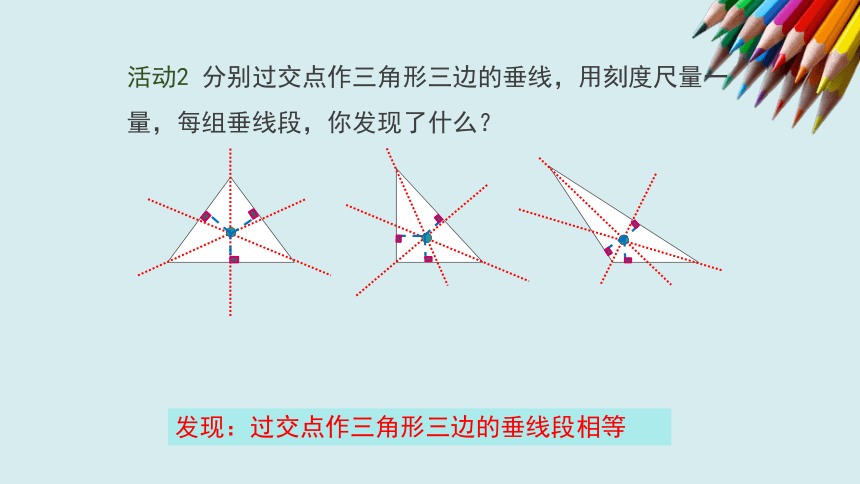
活动2
分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等
例2.
如图,△ABC的角平分线AD,BE,CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
┐
A
可多次利用角平分线的性质证得
∵AD为△ABC的角平分线,∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,
即点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
┐
┐
┐
A
M
E
N
A
B
C
P
O
D
变式1:如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
温馨提示:不存在垂线段———构造应用
12
解:连接OC
M
E
N
A
B
C
P
O
D
变式1:如图,在直角△ABC中,∠C=900,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.
三角形三个内角的平分线的性质
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等.反之,三角形内部到三边距离相等的点是该
三角形三条角平分线的交点.
A
B
C
P
课后练习
1.
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
2.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确
的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
3.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
4.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
5.如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
证明:由题意,得OD⊥BC,OE
⊥
AC,
OF
⊥
AB,
且OF=OD=OE,
∴OB,OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
6.如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
7.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE平分∠DAB.
A
B
C
E
D
┌
┌
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
证明角平分线的方法
只需从要证的线上的某一点向角的两边作(找)垂线段,再证明垂线段相等即可.
∵E是BC的中点,
∴EC=EB
=EF.
又∵EF⊥AD,EB⊥AB,
∴点E在∠DAB的平分线上,即AE平分∠DAB.
F
┌
A
B
C
E
D
┌
┌
12.3
角平分线的性质
第2课时
角平分线的判定
教学目标
1.理解角平分线判定定理.(难点)
2.掌握角平分线判定定理内容的证明方法并应用其解题.(重点)
3.学会判断一个点是否在一个角的平分线上.
复习导入
1、写出命题“全等三角形的对应边相等”的逆命题.
1、写出命题“角平分线上的点到角的两边的距离相等”
的逆命题.
我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
几何语言:
猜想:
角平分线的判定
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
例1.
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
角的平分线的性质定理与判定定理的关系.
点在角的平分线上
(角的内部)点到角的两边的距离相等
性质定理
判定定理
性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
角的平分线的性质定理与判定定理的关系
活动1
分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
三角形的内角平分线
活动2
分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等
例2.
如图,△ABC的角平分线AD,BE,CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
┐
A
可多次利用角平分线的性质证得
∵AD为△ABC的角平分线,∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,
即点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
┐
┐
┐
A
M
E
N
A
B
C
P
O
D
变式1:如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
温馨提示:不存在垂线段———构造应用
12
解:连接OC
M
E
N
A
B
C
P
O
D
变式1:如图,在直角△ABC中,∠C=900,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.
三角形三个内角的平分线的性质
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等.反之,三角形内部到三边距离相等的点是该
三角形三条角平分线的交点.
A
B
C
P
课后练习
1.
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
2.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确
的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
3.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
4.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
5.如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
证明:由题意,得OD⊥BC,OE
⊥
AC,
OF
⊥
AB,
且OF=OD=OE,
∴OB,OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
6.如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
7.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE平分∠DAB.
A
B
C
E
D
┌
┌
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
证明角平分线的方法
只需从要证的线上的某一点向角的两边作(找)垂线段,再证明垂线段相等即可.
∵E是BC的中点,
∴EC=EB
=EF.
又∵EF⊥AD,EB⊥AB,
∴点E在∠DAB的平分线上,即AE平分∠DAB.
F
┌
A
B
C
E
D
┌
┌
