第十二章全等三角形 12.3角的平分线的性质(第一课时)课后练习 2021-2022学年人教版八年级数学上册(word版含答案)
文档属性
| 名称 | 第十二章全等三角形 12.3角的平分线的性质(第一课时)课后练习 2021-2022学年人教版八年级数学上册(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 325.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 08:29:53 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.3角的平分线的性质(第一课时)课后练习
一、选择题
1.如图,的周长是21,,分别平分和,于,且,则的面积为(
)
A.84
B.63
C.42
D.21
2.如图,是的平分线,于点E,,则长是(
)
A.3
B.4
C.6
D.5
3.如图,已知△ABC的周长是16,MB和MC分别是∠ABC和∠ACB角平分线交于M,且MD⊥BC,MD=4,则S△ABC=(
)
A.64
B.48
C.32
D.42
4.如图,数学课上,老师让学生尺规作图画∠MON的角平分线OB.小明的作法如图所示,连接BA、BC,你认为这种作法中判断△ABO≌△CBO的依据是(
)
A.SSS
B.SAS
C.ASA
D.AAS
5.如图,平分,,垂足为,若,,,则的长为(
)
A.3
B.5
C.
D.4
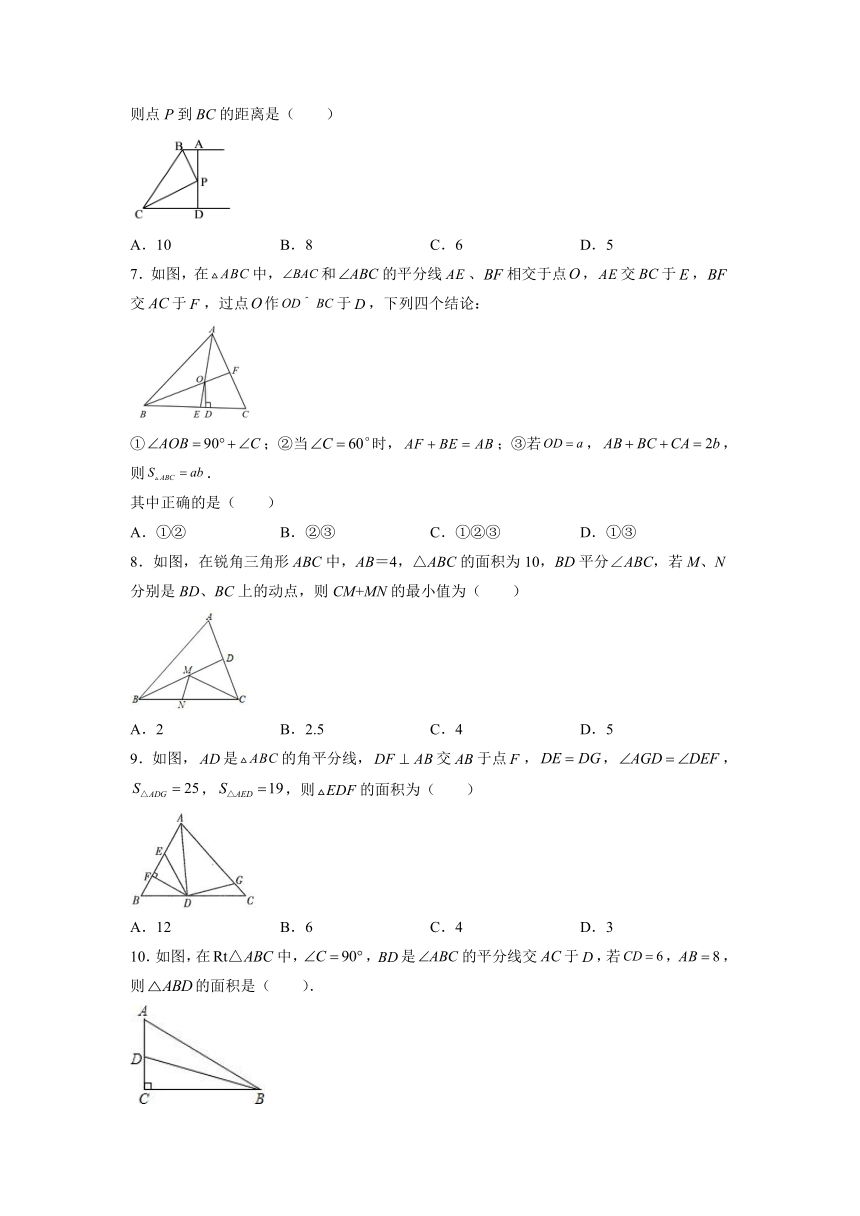
6.如图,AB//CD,BP和CP分别平分∠ABC和∠DCB,AD过点P且与AB垂直,已知AD=10,则点P到BC的距离是(
)
A.10
B.8
C.6
D.5
7.如图,在中,和的平分线、相交于点,交于,交于,过点作于,下列四个结论:
①;②当时,;③若,,则.
其中正确的是(
)
A.①②
B.②③
C.①②③
D.①③
8.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为( )
A.2
B.2.5
C.4
D.5
9.如图,是的角平分线,交于点,,,,,则的面积为(
)
A.12
B.6
C.4
D.3
10.如图,在中,,是的平分线交于,若,,则的面积是(
).
A.24
B.48
C.14
D.无法计算
二、填空题
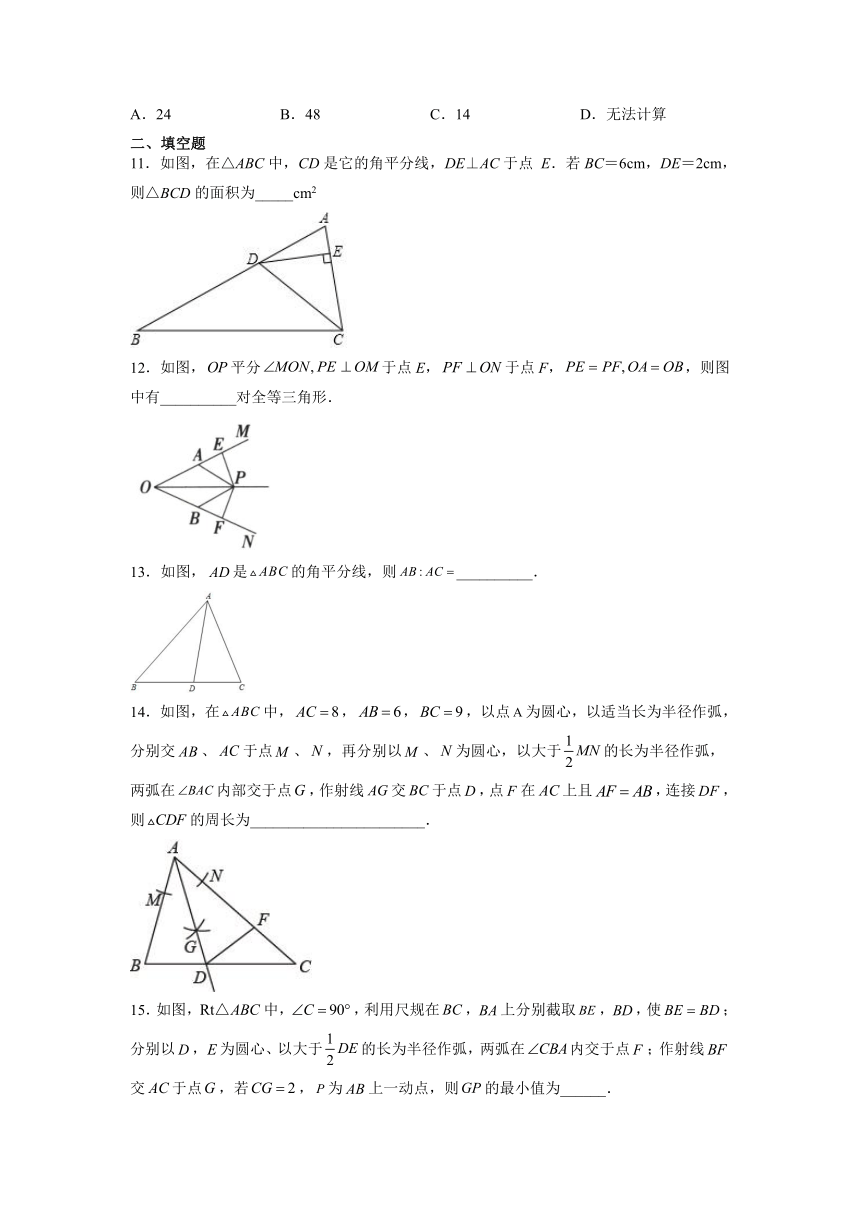
11.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点
E.若BC=6cm,DE=2cm,则△BCD的面积为_____cm2
12.如图,平分于点E,于点F,,则图中有__________对全等三角形.
13.如图,是的角平分线,则__________.
14.如图,在中,,,,以点为圆心,以适当长为半径作弧,分别交、于点、,再分别以、为圆心,以大于的长为半径作弧,两弧在内部交于点,作射线交于点,点在上且,连接,则的周长为_______________________.
15.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点,若,为上一动点,则的最小值为______.
三、解答题
16.如图,,以点A为圆心,小于长为半径作圆弧,分别交、于E、F两点;再分别以点E、F为圆心,大于长为半径作圆弧,两条圆弧交于点G,作射线交于点H.若,求的度数.
17.如图,,O为和的平分线的交点,于点E,且,求两平行线间的距离.
18.如图,的平分线与的平分线交于点P,过点P的直线垂直于,垂足为D,交于点C试问:点P是线段的中点吗?为什么?
19.如图,在中,,,,,若平分交于点,求的长.
20.如图,直线PQ∥MN,一副三角尺(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置,其中点E在直线PQ上,点B,C均在直线MN上,且CE平分∠ACN.
(1)求∠DEQ的度数.
(2)如图②,若将三角形ABC绕点B以每秒3度的速度按逆时针方向旋转(A,C的对应点分别为F,G),设旋转时间为t(s)(0≤t≤60).
①在旋转过程中,若边BG∥CD,求t的值.
②若在三角形ABC绕点B旋转的同时,三角形CDE绕点E以每秒2度的速度按顺时针方向旋转(C,D的对应点为H,K).请直接写出当边BG∥HK时t的值.
21.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
22.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
23.如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之变化?若变化,请找出规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数;若不存在,请说明理由.
【参考答案】
1.C
2.A
3.C
4.A
5.C
6.D
7.B
8.D
9.D
10.A
11.6
12.3
13.BD:DC
14.11
15.2
16.20゜
17.8
点P是线段的中点
19..
20.(1)∠DEQ=60°;(2)①t的值为10s;②当边BG∥HK时,t的值为6s或42s.
21.(1)略;(2)7
22.(1)60°;(2)8
23.(1)30°;(2)不变;1:2;(3)存在,此时∠OEC=45°
第十二章全等三角形
12.3角的平分线的性质(第一课时)课后练习
一、选择题
1.如图,的周长是21,,分别平分和,于,且,则的面积为(
)
A.84
B.63
C.42
D.21
2.如图,是的平分线,于点E,,则长是(
)
A.3
B.4
C.6
D.5
3.如图,已知△ABC的周长是16,MB和MC分别是∠ABC和∠ACB角平分线交于M,且MD⊥BC,MD=4,则S△ABC=(
)
A.64
B.48
C.32
D.42
4.如图,数学课上,老师让学生尺规作图画∠MON的角平分线OB.小明的作法如图所示,连接BA、BC,你认为这种作法中判断△ABO≌△CBO的依据是(
)
A.SSS
B.SAS
C.ASA
D.AAS
5.如图,平分,,垂足为,若,,,则的长为(
)
A.3
B.5
C.
D.4
6.如图,AB//CD,BP和CP分别平分∠ABC和∠DCB,AD过点P且与AB垂直,已知AD=10,则点P到BC的距离是(
)
A.10
B.8
C.6
D.5
7.如图,在中,和的平分线、相交于点,交于,交于,过点作于,下列四个结论:
①;②当时,;③若,,则.
其中正确的是(
)
A.①②
B.②③
C.①②③
D.①③
8.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为( )
A.2
B.2.5
C.4
D.5
9.如图,是的角平分线,交于点,,,,,则的面积为(
)
A.12
B.6
C.4
D.3
10.如图,在中,,是的平分线交于,若,,则的面积是(
).
A.24
B.48
C.14
D.无法计算
二、填空题
11.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点
E.若BC=6cm,DE=2cm,则△BCD的面积为_____cm2
12.如图,平分于点E,于点F,,则图中有__________对全等三角形.
13.如图,是的角平分线,则__________.
14.如图,在中,,,,以点为圆心,以适当长为半径作弧,分别交、于点、,再分别以、为圆心,以大于的长为半径作弧,两弧在内部交于点,作射线交于点,点在上且,连接,则的周长为_______________________.
15.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点,若,为上一动点,则的最小值为______.
三、解答题
16.如图,,以点A为圆心,小于长为半径作圆弧,分别交、于E、F两点;再分别以点E、F为圆心,大于长为半径作圆弧,两条圆弧交于点G,作射线交于点H.若,求的度数.
17.如图,,O为和的平分线的交点,于点E,且,求两平行线间的距离.
18.如图,的平分线与的平分线交于点P,过点P的直线垂直于,垂足为D,交于点C试问:点P是线段的中点吗?为什么?
19.如图,在中,,,,,若平分交于点,求的长.
20.如图,直线PQ∥MN,一副三角尺(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置,其中点E在直线PQ上,点B,C均在直线MN上,且CE平分∠ACN.
(1)求∠DEQ的度数.
(2)如图②,若将三角形ABC绕点B以每秒3度的速度按逆时针方向旋转(A,C的对应点分别为F,G),设旋转时间为t(s)(0≤t≤60).
①在旋转过程中,若边BG∥CD,求t的值.
②若在三角形ABC绕点B旋转的同时,三角形CDE绕点E以每秒2度的速度按顺时针方向旋转(C,D的对应点为H,K).请直接写出当边BG∥HK时t的值.
21.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
22.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
23.如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之变化?若变化,请找出规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数;若不存在,请说明理由.
【参考答案】
1.C
2.A
3.C
4.A
5.C
6.D
7.B
8.D
9.D
10.A
11.6
12.3
13.BD:DC
14.11
15.2
16.20゜
17.8
点P是线段的中点
19..
20.(1)∠DEQ=60°;(2)①t的值为10s;②当边BG∥HK时,t的值为6s或42s.
21.(1)略;(2)7
22.(1)60°;(2)8
23.(1)30°;(2)不变;1:2;(3)存在,此时∠OEC=45°
