河南省渑池县高中2022届高三上学期9月月考数学试题(Word版,含答案)
文档属性
| 名称 | 河南省渑池县高中2022届高三上学期9月月考数学试题(Word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 14:39:17 | ||
图片预览



文档简介
渑池县高级中学2022届高三上学期9月数学月考试卷
一、单选题
1.已知向量
,向量
在
方向上的投影为-4,若
,则实数
的值为(???
)
A.?3??????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
2.函数
的图象向右平移
个单位后所得的图象关于原点对称,则
可以是(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.已知
,
分别为双曲线
的左?右焦点,
为双曲线右支上一点,满足
,则
的面积为(???
)
A.?5???????????????????????????????????????B.?10???????????????????????????????????????C.????????????????????????????????????????D.?
4.已知等比数列
的首项
,公比为
,前
项和为
,则“
”是“
”的(??
)
A.?充分不必要条件???????????B.?必要不充分条件???????????C.?充分必要条件???????????D.?既不充分也不必要条件
5.已知数列
的前
项和为
,且对任意
都有
,设
,则数列
的前5项之和为(???
)
A.?11?????????????????????????????????????????B.?16?????????????????????????????????????????C.?10?????????????????????????????????????????D.?15
6.若不等式
对
恒成立,则
的值等于(???
)
A.
B.
C.1
D.2
7.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设
,用
表示不超过
的最大整数,则
称为高斯函数,例如:
,
,已知函数
,则函数
的值域是(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?{1}
8.在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1CC1所成的角为30°,则该长方体的体积为(
??)
A.?8?????????????????????????????????????B.?6
?????????????????????????????????????C.?8
?????????????????????????????????????D.?8
9.若
的展开式中的各项系数的和为1,则该展开式中的常数项为(??
)
A.?672????????????????????????????????????B.?-672????????????????????????????????????C.?5376????????????????????????????????????D.?-5376
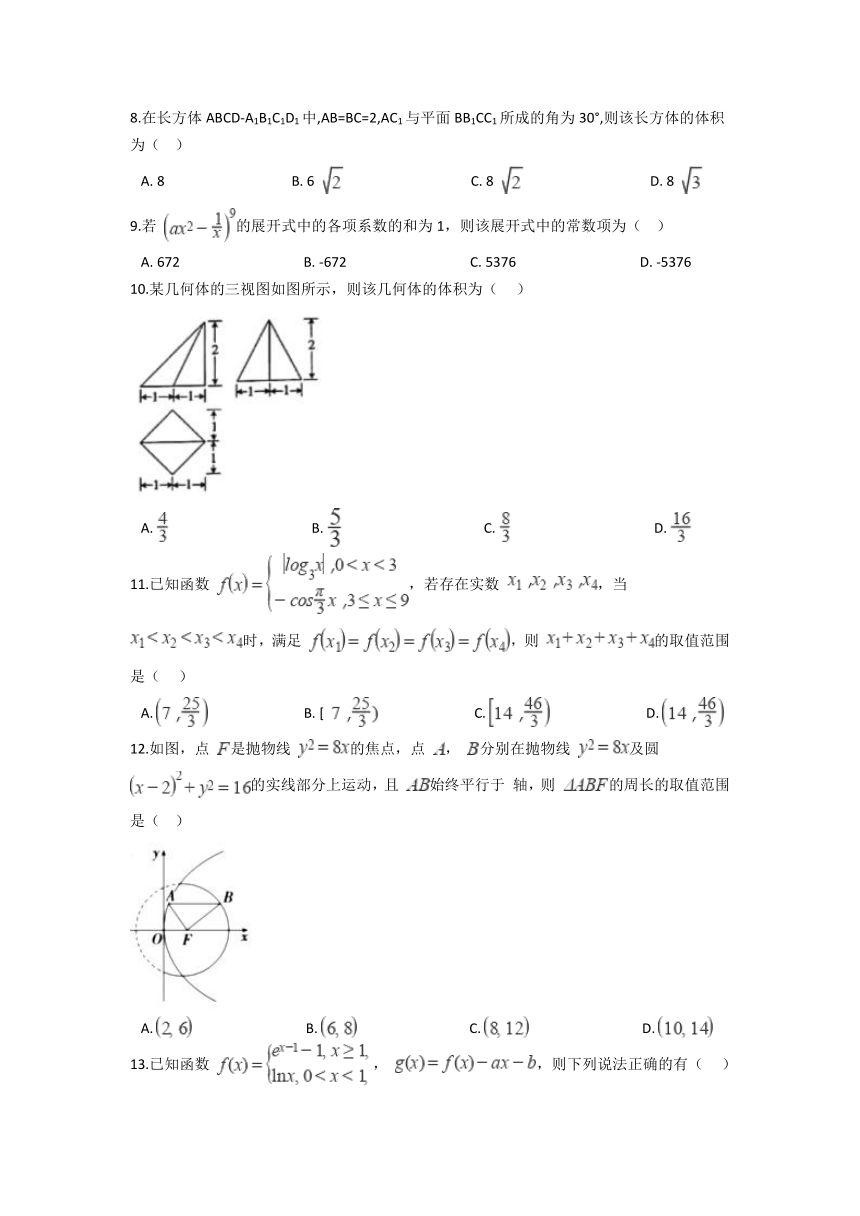
10.某几何体的三视图如图所示,则该几何体的体积为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
11.已知函数
,若存在实数
,当
时,满足
,则
的取值范围是(???
)
A.?????????????????????????????B.?[
????????????????????????????C.?????????????????????????????D.?
12.如图,点
是抛物线
的焦点,点
,
分别在抛物线
及圆
的实线部分上运动,且
始终平行于
轴,则
的周长的取值范围是(?
?)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
13.已知函数
,
,则下列说法正确的有(???
)
①存在
,函数
没有零点;②存在
,函数
恰有三个零点;③任意
,存在
,函数
恰有一个零点;④任意
,存在
,函数
恰有二个零点;
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
14.在棱长均相等的正三棱柱
中,
为
的中点,
在
上,且
,则下述结论:①
;②
;③平面
平面
:④异面直线
与
所成角为
其中正确命题的个数为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
15.已知函数
,方程
恰有两个不同的实数根
、
,则
的最小值与最大值的和(???
)
A.?????????????????????????????????????B.?2????????????????????????????????????C.?????????????????????????????????????D.?
16.已知函数
在
处取得极值,若
,则
的最小值为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?0?????????????????????????????????????????D.?2
17.将函数
的图象向右平移
个单位长度得到
的图象,若函数
在区间
上单调递增,且
的最大负零点在区间
上,则
的取值范围是(????
)
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
18.一个多面体的三视图如图所示,则该多面体的体积为(???
)
A.?7???????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
19.将棱长相等的正方体按如右图所示的形状摆放,
从上往下依次为第1层,
第2层,
第3层…….
则第2005层正方体的个数是(???
)
A.4011
B.4009
C.2011015
D.2009010
20.若对任意x∈(0,π),不等式ex﹣e﹣x>asinx恒成立,则实数a的取值范围是(??
)
A.?[﹣2,2]?????????????????????????B.?(﹣∞,e]?????????????????????????C.?(﹣∞,2]?????????????????????????D.?(﹣∞,1]
二、填空题
21..已知某几何体的三视图如图所示,则该几何体的表面积为???1???
,
体积为???2???
.
22.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成,因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看成所有棱长均为
的正四棱锥,则这个粽子的表面积为________
.现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,其半径与正四棱锥的高的比值为________.
23.过
作与双曲线
(
,
的两条渐近线平行的直线,分别交两渐近线于A、B两点,若
四点共圆(为坐标原点),则双曲线的离心率为________.
24.已知函数
,则方程
?的解的个数为________.
25.在直角坐标平面上,已知点A(0,2),B(0,1),D(t,0)(t>0).点M是线段AD上的动点,如果|AM|≤2|BM|恒成立,则正实数t的最小值是________.
26.设函数f(x)=(2x﹣1)ex﹣ax+a,若存在唯一的整数x0使得f(x0)<0,则实数a的取值范围是________.
27.已知函数
,若对于任意正实数
,均存在以
为三边边长的三角形,则实数k的取值范围是________.
三、解答题
28.已知实数正数x,y满足
.
(1)解关于x的不等式
;
(2)证明:
?
29.设数列
的前
项和为
,已知
,
.
(1)求通项公式
;
(2)设
,求数列
的前
项和
.
30.已知椭圆C:
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
.
(I)求椭圆C的方程;
(II)设过点B(0,m)(m>0)的直线与椭圆C相交于E,F两点,点B关于原点的对称点为D,若点D总在以线段EF为直径的圆内,求m的取值范围.
31..已知函数f(x)=|x﹣1|+|x﹣t|(t∈R)
(1).t=2时,求不等式f(x)>2的解集;
(2).若对于任意的t∈[1,2],x∈[﹣1,3],f(x)≥a+x恒成立,求实数a的取值范围.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
B
3.【答案】
A
4.【答案】
A
5.【答案】
C
6.【答案】
B
7.【答案】
A
8.【答案】
C
9.【答案】
A
10.【答案】
A
11.【答案】
D
12.【答案】
C
13.【答案】
B
14.【答案】
B
15.【答案】
C
16.【答案】
A
17.【答案】
B
18.【答案】
C
19.【答案】
C
20.【答案】C
二、填空题
21.【答案】
2+2
;
22.【答案】
;
23.【答案】
24.【答案】
5
25.【答案】
26.【答案】
[
,1)∪
27.【答案】
三、解答题
28.【答案】
(1)解:
解得
,所以不等式的解集为
(2)解:解法1:
且
,
?
?
?
.
当且仅当
时,等号成立.
解法2:
且
,
?
?
?
当且仅当
时,等号成立.
29.【答案】
(1)解:
,
相减得:
?????
????
,
又
,∴
∴
(2)解:
30.【答案】
解:(I)由题意,得:
又因为
解得
,所以椭圆C的方程为
.
(II)当直线的斜率不存在时,由题意知的方程为x=0,
此时E,F为椭圆的上下顶点,且
,
因为点
总在以线段
为直径的圆内,且
,
所以
,故点B在椭圆内.
当直线的斜率存在时,设的方程为
.
由方程组
得
,
因为点B在椭圆内,
所以直线与椭圆C有两个公共点,即
.
设
,则
.
设EF的中点
,则
,
所以
.所以
,
,
因为点D总在以线段EF为直径的圆内,所以
对于
恒成立.
所以
.
化简,得
,整理,得
,
而
(当且仅当k=0时等号成立)所以
,
由m>0,得
.综上,m的取值范围是
.
31.【答案】
(1)解:当t=2时,f(x)=|x﹣1|+|x﹣2|,
若x≤1,则f(x)=3﹣2x,于是由f(x)>2,解得x<
,综合得x<
;
若1<x<2,则f(x)=1,显然f(x)>2不成立;
若x≥2,则f(x)=2x﹣3,于是由f(x)>2,解得x>
,综合得x>
∴不等式f(x)>2的解集为{x|x<
,或x>
}
(2)解:f(x)≥a+x等价于a≤f(x)﹣x,令g(x)=f(x)﹣x,
当﹣1≤x≤1时,g(x)=1+t﹣3x,显然g(x)min=g(1)=t﹣2,
当1<x<t时,g(x)=t﹣1﹣x,此时g(x)>g(1)=t﹣2,
当t≤x≤3时,g(x)=x﹣t﹣1,g(x)min=g(1)=t﹣2,
∴当x∈[1,3]时,g(x)min=t﹣2,
又∵t∈[1,2],
∴g(x)min≤﹣1,即a≤﹣1,
综上,a的取值范围是a≤﹣1
一、单选题
1.已知向量
,向量
在
方向上的投影为-4,若
,则实数
的值为(???
)
A.?3??????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
2.函数
的图象向右平移
个单位后所得的图象关于原点对称,则
可以是(??
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.已知
,
分别为双曲线
的左?右焦点,
为双曲线右支上一点,满足
,则
的面积为(???
)
A.?5???????????????????????????????????????B.?10???????????????????????????????????????C.????????????????????????????????????????D.?
4.已知等比数列
的首项
,公比为
,前
项和为
,则“
”是“
”的(??
)
A.?充分不必要条件???????????B.?必要不充分条件???????????C.?充分必要条件???????????D.?既不充分也不必要条件
5.已知数列
的前
项和为
,且对任意
都有
,设
,则数列
的前5项之和为(???
)
A.?11?????????????????????????????????????????B.?16?????????????????????????????????????????C.?10?????????????????????????????????????????D.?15
6.若不等式
对
恒成立,则
的值等于(???
)
A.
B.
C.1
D.2
7.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设
,用
表示不超过
的最大整数,则
称为高斯函数,例如:
,
,已知函数
,则函数
的值域是(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?{1}
8.在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1CC1所成的角为30°,则该长方体的体积为(
??)
A.?8?????????????????????????????????????B.?6
?????????????????????????????????????C.?8
?????????????????????????????????????D.?8
9.若
的展开式中的各项系数的和为1,则该展开式中的常数项为(??
)
A.?672????????????????????????????????????B.?-672????????????????????????????????????C.?5376????????????????????????????????????D.?-5376
10.某几何体的三视图如图所示,则该几何体的体积为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
11.已知函数
,若存在实数
,当
时,满足
,则
的取值范围是(???
)
A.?????????????????????????????B.?[
????????????????????????????C.?????????????????????????????D.?
12.如图,点
是抛物线
的焦点,点
,
分别在抛物线
及圆
的实线部分上运动,且
始终平行于
轴,则
的周长的取值范围是(?
?)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
13.已知函数
,
,则下列说法正确的有(???
)
①存在
,函数
没有零点;②存在
,函数
恰有三个零点;③任意
,存在
,函数
恰有一个零点;④任意
,存在
,函数
恰有二个零点;
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
14.在棱长均相等的正三棱柱
中,
为
的中点,
在
上,且
,则下述结论:①
;②
;③平面
平面
:④异面直线
与
所成角为
其中正确命题的个数为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
15.已知函数
,方程
恰有两个不同的实数根
、
,则
的最小值与最大值的和(???
)
A.?????????????????????????????????????B.?2????????????????????????????????????C.?????????????????????????????????????D.?
16.已知函数
在
处取得极值,若
,则
的最小值为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?0?????????????????????????????????????????D.?2
17.将函数
的图象向右平移
个单位长度得到
的图象,若函数
在区间
上单调递增,且
的最大负零点在区间
上,则
的取值范围是(????
)
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
18.一个多面体的三视图如图所示,则该多面体的体积为(???
)
A.?7???????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
19.将棱长相等的正方体按如右图所示的形状摆放,
从上往下依次为第1层,
第2层,
第3层…….
则第2005层正方体的个数是(???
)
A.4011
B.4009
C.2011015
D.2009010
20.若对任意x∈(0,π),不等式ex﹣e﹣x>asinx恒成立,则实数a的取值范围是(??
)
A.?[﹣2,2]?????????????????????????B.?(﹣∞,e]?????????????????????????C.?(﹣∞,2]?????????????????????????D.?(﹣∞,1]
二、填空题
21..已知某几何体的三视图如图所示,则该几何体的表面积为???1???
,
体积为???2???
.
22.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成,因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看成所有棱长均为
的正四棱锥,则这个粽子的表面积为________
.现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,其半径与正四棱锥的高的比值为________.
23.过
作与双曲线
(
,
的两条渐近线平行的直线,分别交两渐近线于A、B两点,若
四点共圆(为坐标原点),则双曲线的离心率为________.
24.已知函数
,则方程
?的解的个数为________.
25.在直角坐标平面上,已知点A(0,2),B(0,1),D(t,0)(t>0).点M是线段AD上的动点,如果|AM|≤2|BM|恒成立,则正实数t的最小值是________.
26.设函数f(x)=(2x﹣1)ex﹣ax+a,若存在唯一的整数x0使得f(x0)<0,则实数a的取值范围是________.
27.已知函数
,若对于任意正实数
,均存在以
为三边边长的三角形,则实数k的取值范围是________.
三、解答题
28.已知实数正数x,y满足
.
(1)解关于x的不等式
;
(2)证明:
?
29.设数列
的前
项和为
,已知
,
.
(1)求通项公式
;
(2)设
,求数列
的前
项和
.
30.已知椭圆C:
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
.
(I)求椭圆C的方程;
(II)设过点B(0,m)(m>0)的直线与椭圆C相交于E,F两点,点B关于原点的对称点为D,若点D总在以线段EF为直径的圆内,求m的取值范围.
31..已知函数f(x)=|x﹣1|+|x﹣t|(t∈R)
(1).t=2时,求不等式f(x)>2的解集;
(2).若对于任意的t∈[1,2],x∈[﹣1,3],f(x)≥a+x恒成立,求实数a的取值范围.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
B
3.【答案】
A
4.【答案】
A
5.【答案】
C
6.【答案】
B
7.【答案】
A
8.【答案】
C
9.【答案】
A
10.【答案】
A
11.【答案】
D
12.【答案】
C
13.【答案】
B
14.【答案】
B
15.【答案】
C
16.【答案】
A
17.【答案】
B
18.【答案】
C
19.【答案】
C
20.【答案】C
二、填空题
21.【答案】
2+2
;
22.【答案】
;
23.【答案】
24.【答案】
5
25.【答案】
26.【答案】
[
,1)∪
27.【答案】
三、解答题
28.【答案】
(1)解:
解得
,所以不等式的解集为
(2)解:解法1:
且
,
?
?
?
.
当且仅当
时,等号成立.
解法2:
且
,
?
?
?
当且仅当
时,等号成立.
29.【答案】
(1)解:
,
相减得:
?????
????
,
又
,∴
∴
(2)解:
30.【答案】
解:(I)由题意,得:
又因为
解得
,所以椭圆C的方程为
.
(II)当直线的斜率不存在时,由题意知的方程为x=0,
此时E,F为椭圆的上下顶点,且
,
因为点
总在以线段
为直径的圆内,且
,
所以
,故点B在椭圆内.
当直线的斜率存在时,设的方程为
.
由方程组
得
,
因为点B在椭圆内,
所以直线与椭圆C有两个公共点,即
.
设
,则
.
设EF的中点
,则
,
所以
.所以
,
,
因为点D总在以线段EF为直径的圆内,所以
对于
恒成立.
所以
.
化简,得
,整理,得
,
而
(当且仅当k=0时等号成立)所以
,
由m>0,得
.综上,m的取值范围是
.
31.【答案】
(1)解:当t=2时,f(x)=|x﹣1|+|x﹣2|,
若x≤1,则f(x)=3﹣2x,于是由f(x)>2,解得x<
,综合得x<
;
若1<x<2,则f(x)=1,显然f(x)>2不成立;
若x≥2,则f(x)=2x﹣3,于是由f(x)>2,解得x>
,综合得x>
∴不等式f(x)>2的解集为{x|x<
,或x>
}
(2)解:f(x)≥a+x等价于a≤f(x)﹣x,令g(x)=f(x)﹣x,
当﹣1≤x≤1时,g(x)=1+t﹣3x,显然g(x)min=g(1)=t﹣2,
当1<x<t时,g(x)=t﹣1﹣x,此时g(x)>g(1)=t﹣2,
当t≤x≤3时,g(x)=x﹣t﹣1,g(x)min=g(1)=t﹣2,
∴当x∈[1,3]时,g(x)min=t﹣2,
又∵t∈[1,2],
∴g(x)min≤﹣1,即a≤﹣1,
综上,a的取值范围是a≤﹣1
同课章节目录
