人教版八年级数学上册第十三章 轴对称13.1.2 第1课时 线段垂直平分线的性质课件(24张ppt)
文档属性
| 名称 | 人教版八年级数学上册第十三章 轴对称13.1.2 第1课时 线段垂直平分线的性质课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 08:34:42 | ||
图片预览






文档简介
(共24张PPT)
第十三章
轴对称
13.1.2
第1课时
线段垂直平分线的性质
教学目标
1.了解轴对称及线段垂直平分线的性质和判定.
2.会应用线段垂直平分线的性质和判定解题.
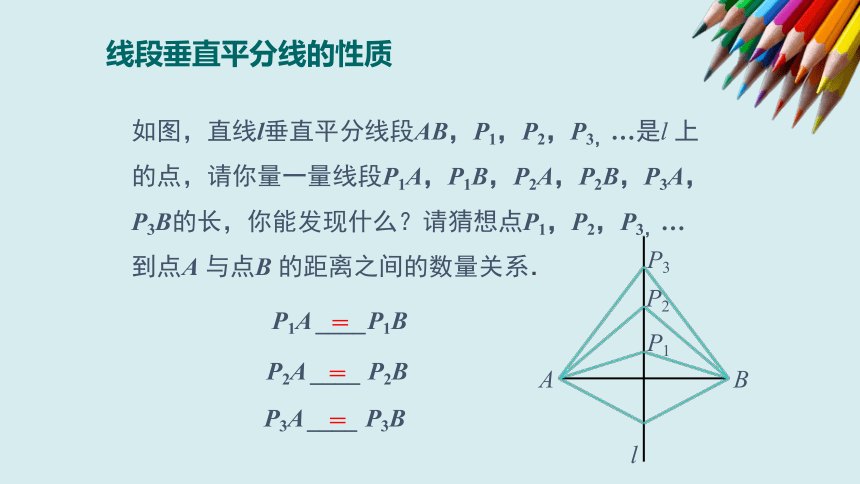
如图,直线l垂直平分线段AB,P1,P2,P3,…是l
上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,…
到点A
与点B
的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A
____P1B
P2A
____
P2B
P3A
____
P3B
=
=
=
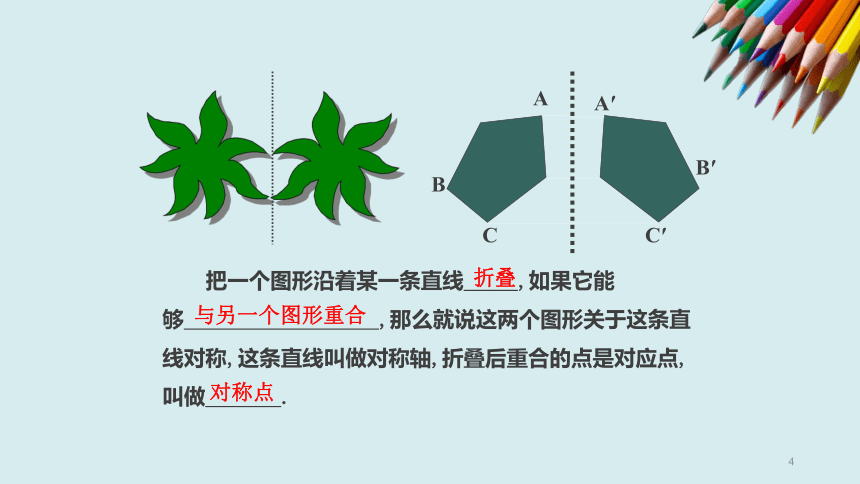
线段垂直平分线的性质
猜想:
点P1,P2,P3,…
到点A
与点B
的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
P
A
B
l
C
验证结论
例1
如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).故选C.
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
例2.尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C
.
求作:AB的垂线,使它经过点C
.
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C
为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F.
F
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
线段垂直平分线的判定
PA
=PB,PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
P
A
B
C
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
证明:过点P
作AB
的垂线PC,垂足为点C.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定
这些点能组成什么几何图形?
你能再找一些到线段AB
两端点的距离相等的点吗?能找到多少个到线段AB
两端点距离相等的点?
与A,B
的距离相等的点都在直线l上,所以直线l
可以看成与A、B两点
的距离相等的所有点的集合.
P
A
B
C
l
例3.已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴
OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
3.如图所示,AC=AD,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B
.CD垂直平分AB
;
C.AB与CD互相垂直平分;
D.CD平分∠
ACB
.
A
B
C
D
A
4.在锐角三角形ABC内一点P,满足PA=PB=PC,
则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是
cm.
A
B
C
D
E
16
6.已知:如图,点C,D是线段AB外的两点,且AC
=BC,
AD=BD,AB与CD相交于点O.
求证:AO=BO.
证明:
∵
AC
=BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴
CD为线段AB的垂直平分线.
又
∵AB与CD相交于点O,
∴
AO=BO.
课堂小结
通过本课时的学习,需要我们:
1.了解轴对称及线段的垂直平分线的有关性质;
2.会灵活运用这些性质来解决问题.
第十三章
轴对称
13.1.2
第1课时
线段垂直平分线的性质
教学目标
1.了解轴对称及线段垂直平分线的性质和判定.
2.会应用线段垂直平分线的性质和判定解题.
如图,直线l垂直平分线段AB,P1,P2,P3,…是l
上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,…
到点A
与点B
的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A
____P1B
P2A
____
P2B
P3A
____
P3B
=
=
=
线段垂直平分线的性质
猜想:
点P1,P2,P3,…
到点A
与点B
的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
P
A
B
l
C
验证结论
例1
如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).故选C.
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
例2.尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C
.
求作:AB的垂线,使它经过点C
.
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C
为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F.
F
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
线段垂直平分线的判定
PA
=PB,PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
P
A
B
C
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
证明:过点P
作AB
的垂线PC,垂足为点C.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定
这些点能组成什么几何图形?
你能再找一些到线段AB
两端点的距离相等的点吗?能找到多少个到线段AB
两端点距离相等的点?
与A,B
的距离相等的点都在直线l上,所以直线l
可以看成与A、B两点
的距离相等的所有点的集合.
P
A
B
C
l
例3.已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴
OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
3.如图所示,AC=AD,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B
.CD垂直平分AB
;
C.AB与CD互相垂直平分;
D.CD平分∠
ACB
.
A
B
C
D
A
4.在锐角三角形ABC内一点P,满足PA=PB=PC,
则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是
cm.
A
B
C
D
E
16
6.已知:如图,点C,D是线段AB外的两点,且AC
=BC,
AD=BD,AB与CD相交于点O.
求证:AO=BO.
证明:
∵
AC
=BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴
CD为线段AB的垂直平分线.
又
∵AB与CD相交于点O,
∴
AO=BO.
课堂小结
通过本课时的学习,需要我们:
1.了解轴对称及线段的垂直平分线的有关性质;
2.会灵活运用这些性质来解决问题.
